[有监督学习]1.详细图解线性回归

news2025/1/17 5:51:59

线性回归（linear regression）是用于预测回归问题的算法。该算法不难理解，算法中根据训练数据计算使损失最小的参数的做法是有监督学习算法的共同之处。

概述
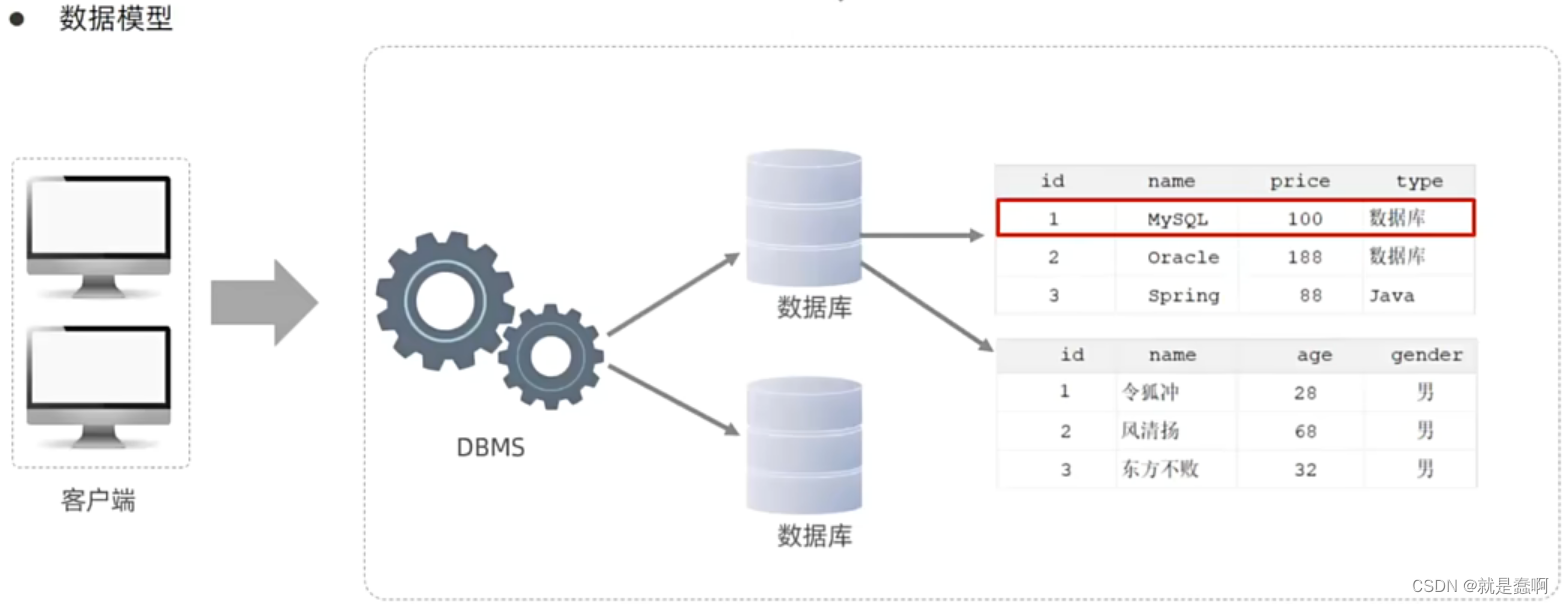
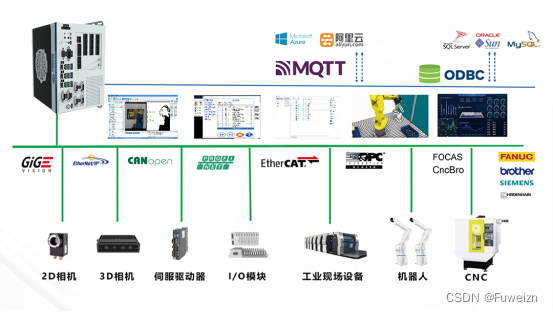
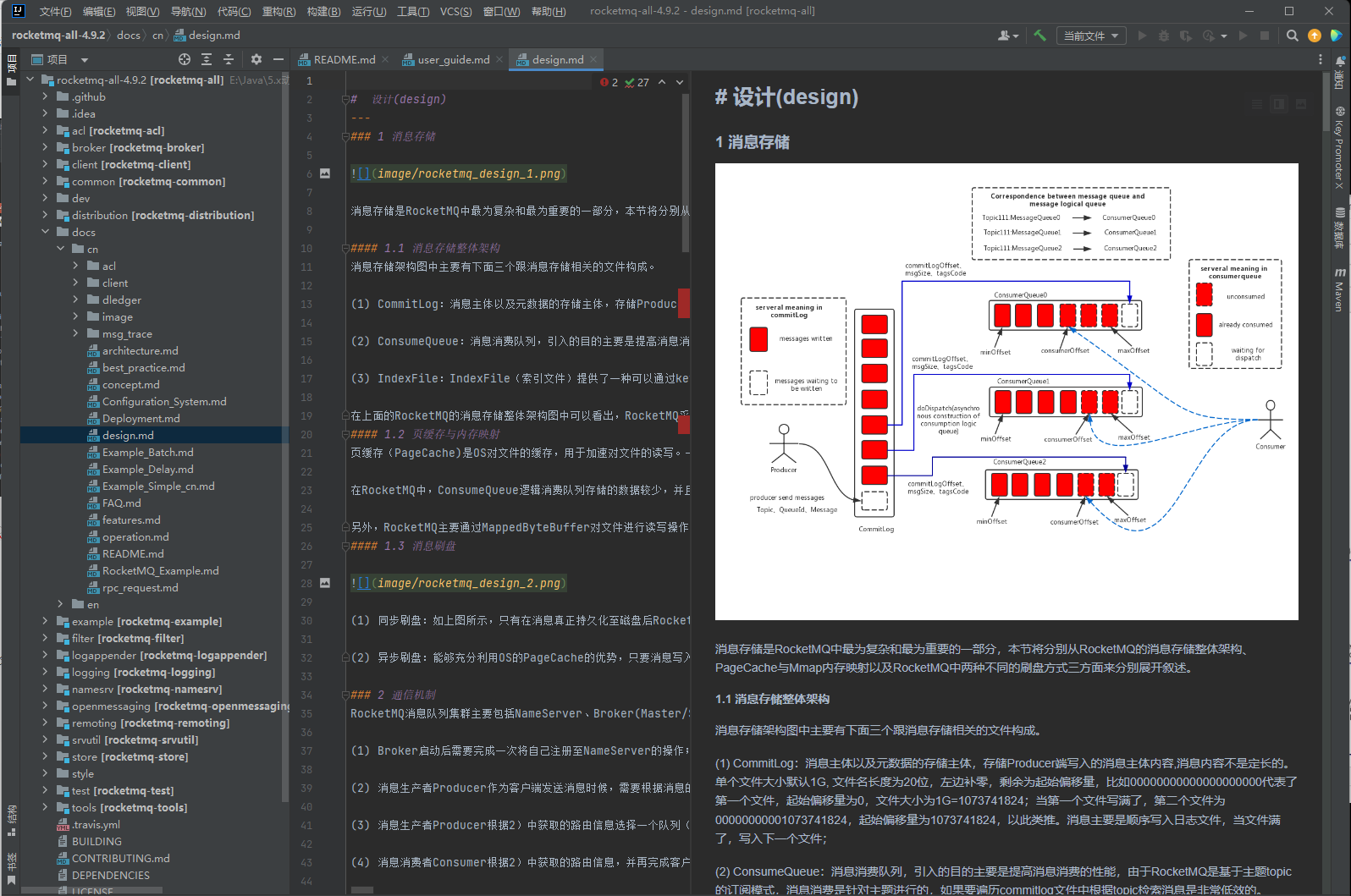
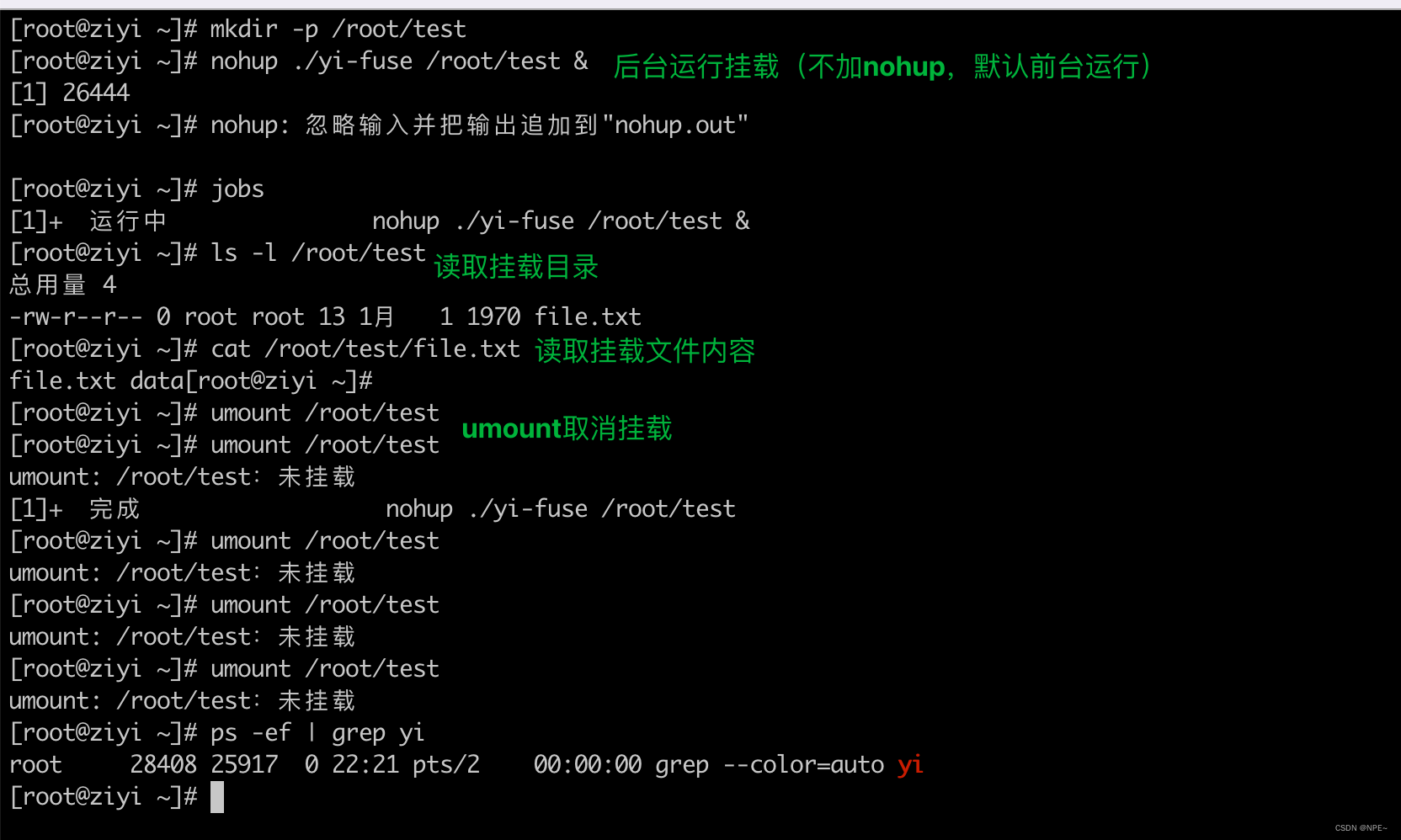
线性回归是对“目标变量随着某个特征变量的增大而增大（或者减小）”这种关联性建模的方法。这里以表 2-1 所示的特征变量x和目标变量y的组合数据为例。图 2-1 是对该数据进行线性回归建模而得到的直线。
▼表 2-1　特征变量 [插图] 和目标变量 [插图] 的组合数据

▲图 2-1　线性回归
图 2-1 的直线可写为这是我们在中学阶段学过的一次函数，w1 是斜率（或者叫权重），w0 相当于在 y 轴上的截距。斜率w1和截距 w0 是由有监督学习的算法学到的参数，所以我们称之为学习参数。线性回归的学习参数是如何求得的呢？下面的“算法说明”部分将对此进行讲解。
另外，线性回归算法一般使用一个以上的特征变量创建模型，其中只有一个独立的特征变量的情况叫作一元回归。

算法说明
对于直线，只要给定不同的两个点，我们就能求出唯一的 w0 和 w1。但在线性回归中，我们需要根据不在一条直线上的点求出学习参数。下面使用表 2-2 的数据介绍学习参数的求法。

▼表 2-2　用于线性回归的数据

图 2-2a 和图 2-2b 是根据表 2-2 的数据绘制的两条不同的直线，分别是，。这两条直线中的哪一条更好地表示了数据的关联性呢？我们可以通过均方误差进行定量判断。均方误差指的是目标变量和直线的差的平方的平均值。当存在n 个数据时，可如下表示：

对图 2-2 的数据计算均方误差，得到图 2-2a 的均方误差约为 2.89，图 2-2b 的均方误差约为 5.83，前者的均方误差更小，因此图 2-2a 能比图 2-2b 更好地表示数据的关联性。

▲图 2-2　均方误差的比较

现在我们知道图 2-2a、图 2-2b 这两条直线的均方误差的值是不同的。
这两条直线的区别就是学习参数w0、w1。也就是说，改变学习参数 w0、w1，那么计算出的均方误差也会发生变化。这种表示误差和学习参数之间关系的函数叫作误差函数（或损失函数）。线性回归需要在各条直线中找出使误差函数值最小的参数（更具体的计算方法请参考后文的“均方误差的最小化方法”部分）。这种计算出使误差函数值最小的参数的思路在其他有监督学习算法中也是通用的。

示例代码
下面尝试对前面的表 2-1 的数据进行线性回归。使用 LinearRegression 类创建线性回归模型，并使用 fit 方法训练后，输出 intercept_ 的值以查看截距，输出 coef_ 的值以查看斜率。
▼示例代码

from sklearn.linear_model import LinearRegression
X = [[10.0], [8.0], [13.0], [9.0], [11.0], [14.0], [6.0], [4.0], [12.0], [7.0], [5.0]]
y = [8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68]
model = LinearRegression()
model.fit(X, y)
print(model.intercept_) # 截距
print(model.coef_) # 斜率
y_pred = model.predict([[0], [1]])
print(y_pred) # 对x=0，x=1的预测结果

结果：

3.0000909090909094

[0.50009091]

[3.00009091 3.50018182]

详细说明
线性回归不成功的例子
我们发现线性回归适用于表 2-1 的数据，但是对于有些数据，线性回归可能不成功。
表 2-1 及示例代码中使用的数据是由统计学家 F.J. 安斯库姆（F.J. Anscombe）制作的数据集安斯库姆四重奏（Anscombe's Quartet）中的一部分。这个数据集的目的是说明可视化的重要性，其中汇总了包含表 2-1 在内的 4 组数据。
图 2-3 显示了对安斯库姆四重奏数据集的每一组数据分别进行线性回归的结果。尽管图 2-3 中的 4 张图是不同的散点图，但线性回归的学习参数（截距和斜率）却相同。另外，这些数据的平均值、方差和相关系数也几乎相同。

▲图 2-3　对安斯库姆四重奏数据集应用线性回归

下面来仔细看一下各组数据。图 2-3b 的数据看上去是沿曲线分布的，所以假定这组数据是线性分布的就不合适。图 2-3c 中有离群值，应考虑对其进行去除离群值的预处理，或者应用便于处理离群值的其他方法。图 2-3d 是对数据两两之间没有相关关系但存在离群值的数据集应用线性回归而得到回归直线的例子。对原本不遵循线性分布的数据强行进行线性回归也得不到好的结果。拿到数据之后，首先应该进行可视化，再考虑是否进行线性回归。

均方误差的最小化方法
在“算法说明”部分，我们了解了均方误差可用于评估具有不同学习参数的直线。
然而，虽然通过如表 2-3 所示的数据比较了不同的学习参数产生的误差大小，但我们还不了解具体的学习参数的计算方法。

▼表 2-3　学习参数和均方误差的关系

从表 2-3 可以看出，由于学习参数的变化，作为误差函数的均方误差也会发生变化。也就是说，均方误差可以使用学习参数的函数表示：

这时将表 2-2 的数据代入目标变量yi和特征变量xi，就可以仅用 w0、w1 表示均方误差：

该式是 w0、w1 的二次函数，函数图形如图 2-4 所示。从图 2-4 可以看出，当 w0、w1 发生变化时，误差的值也各不相同。另外，图 2-4 上标记星号的点对应于表 2-3 中的两种情况。表 2-3 中的 (a) 的学习参数与误差函数取最小值时的学习参数一致，可以看出这是数据点的最佳学习参数。

▲图 2-4　均方误差的最小化

各种线性回归和非线性回归
本节主要说明了一元回归。一元回归是指独立特征变量只有一个时的线性回归，独立特征变量为两个及以上时的线性回归叫作多元回归。另外，尽管独立特征变量只有一个，但包含这种特征变量的次方项的线性回归叫作多项式回归。表 2-4 列出了一元回归、多元回归、多项式回归的例子，图 2-5 展示了与这些例子相应的图形。多项式回归对于特征变量不是线性的，所以称之为“线性”回归可能让人觉得不太合适。

▲图 2-5　各种线性回归的例子
但是，是否为线性回归不是从特征变量来看的。从学习参数（在这个例子中是的系数）的角度来看是线性的回归，我们才称为线性回归，所以多项式回归也属于线性回归。
▼表 2-4　各种线性回归的例子

下面再看一下非线性回归的例子。图 2-6 是和的图形。这些函数中的学习参数 w1和目标变量 y 之间的关系不是线性关系，所以被分类为非线性回归。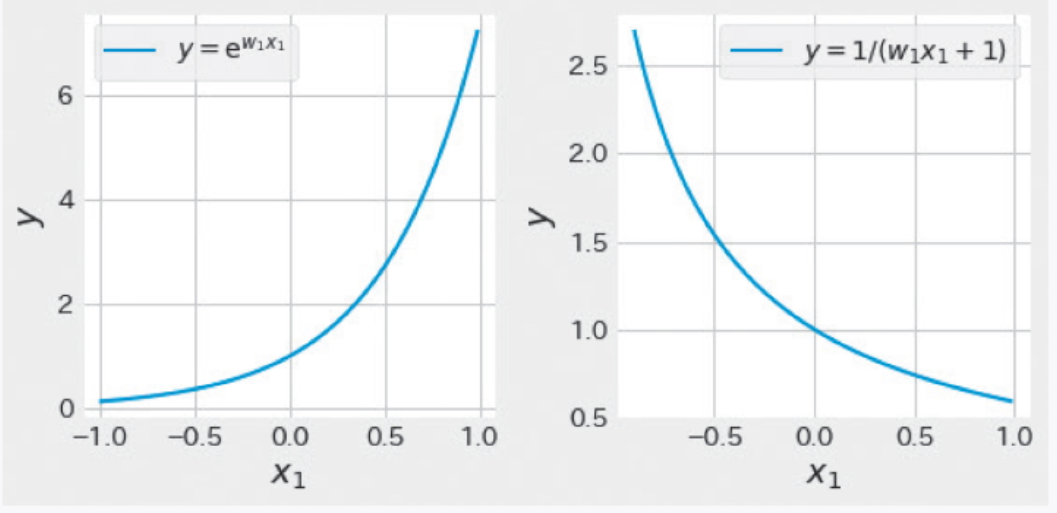

▲图 2-6　非线性回归的例子