什么是空间复杂度？

代码在运行之前需要先装入内存，程序代码需要占一定的位置（在这边假设是100B）
定义的变量和参数i，n都需要占用内存空间

//算法一——逐步递增型
void loveYou(int n) {  //n为问题规模
	int i = 1;  //爱你的程度
	while(i <= n){
		i++;  //每次+1
		printf("I Love You %d\n", i);
	}
	printf("I Love You More Than %d\n", n);
}

int main(){
	loveYou(3000);
}

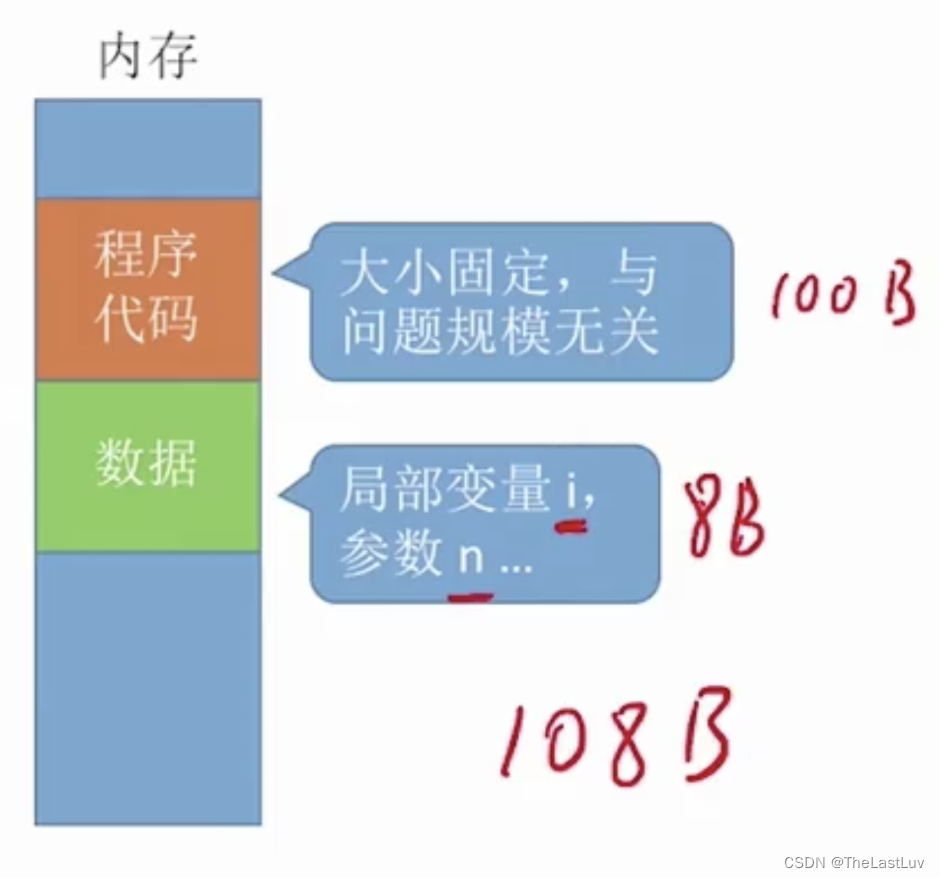
不难发现，无论问题规模怎么变，算法运行所需要的内存空间都是固定常量，算法的空间复杂度表示为：
$$S(n)=O(1)$$

注：S表示Space

算法原地工作——指的是：算法所需内存空间为常量

void test(int n){
	int flag[n];  //声明一个长度为n的数组
	int i;
	//...此处省略很多代码
}

假设一个int变量占4B，则所需内存空间= 4 + 4n + 4 = 4n + 8
$$S(n)=O(4n+8)=O(n)$$

---

void test(int n){
	int flag[n][n];  //声明一个n*n的数组
	int i;
	//...此处省略很多代码
}

$$S(n)=O(n^2)$$

---

void test(int n){
	int flag[n][n];  //声明一个n*n的二维数组
	int other[n];  //声明一个长度为n的数组
	int i;
	//...此处省略很多代码
}

$$S(n)=O(n^2)+O(n)+o(1)=O(n^2)$$

函数递归调用带来的内存开销

void loveYou(int n){  //n为问题规模
	int a,b,c;  //声明一系列局部变量
	//...省略代码
	if(n>1){
		loveYou(n-1);
	}
	printf("I Love You %d\n", i);
}

int main(){
	loveYou(5);
}

最终运行的结果：

代码运行过程分析

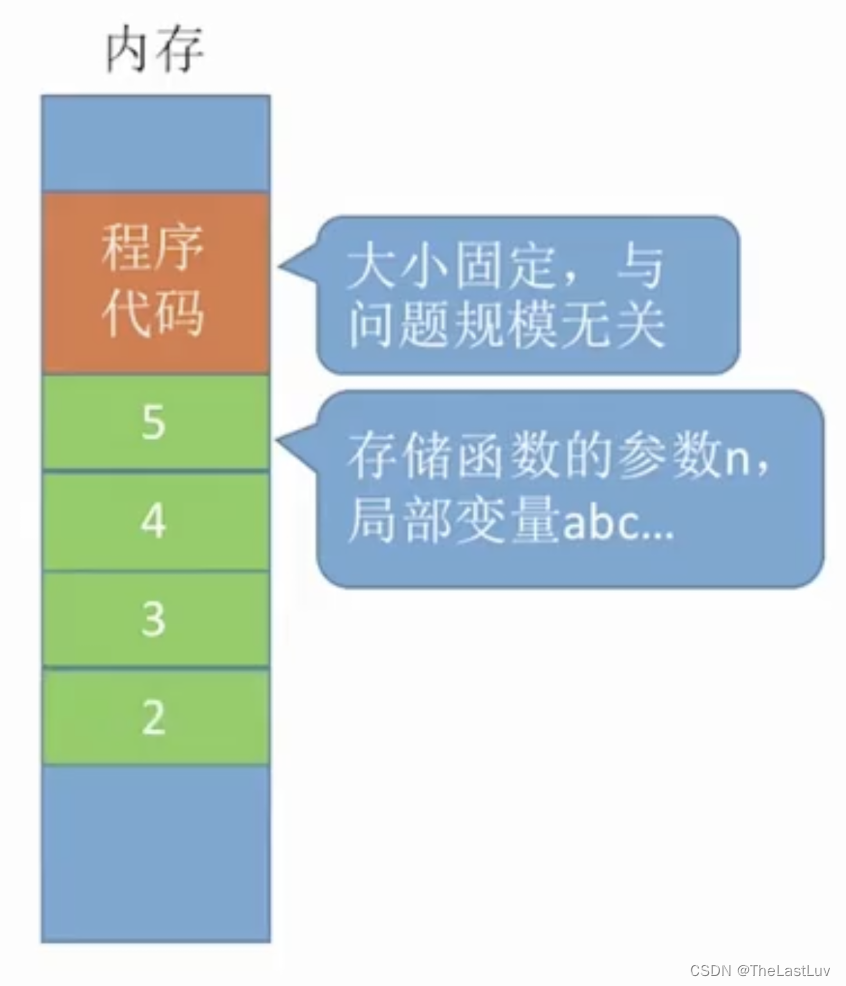
首先是程序代码，大小固定，与问题规模无关
其次是存储函数的参数n，局部变量a, b, c

• 当n=5，要声明变量a, b, c
• 当n= 4，要声明变量a, b, c
• ……
  具体实现过程如图所示：
  

在最后loveYou(1)执行时，发现不满足n>1的条件，计算机会在内存中返回n=2，也就是loveYou(2)时的状态
如下图所示：

void loveYou(int n){
	int flag[n];  //声明一个长度为n的数组
	//...省略部分代码
	if(n>1){
		loveYou(n-1);
	}
	printf("I Love You %d\n", i);
}

int main(){
	 loveYou(5);
}

由于定义的是一个数组，并且长度为n，所以每次根据传入参数的不同，数组的长度，即占用的内存空间，是不一样的
内存空间如图所示：

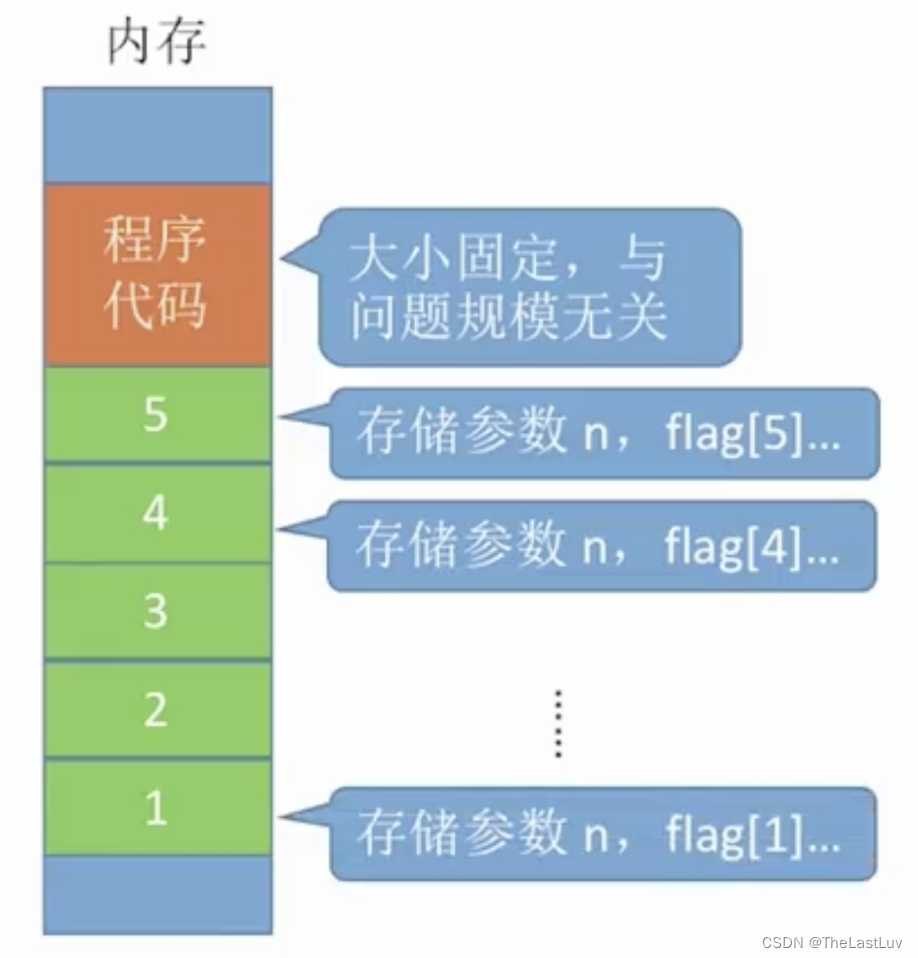
不难发现，第1级的调用数组长度为1，第2级的为2，第3级的为3……
所以各级的空间大小总共为：
$$1+2+3+...+n=\frac{[n(1+n)]}{2}=\frac{1}{2}{n}^2+\frac{1}{2}n$$
所以空间复杂度为：
$$S(n)=O(n^2)$$