目录

一、线性回归

1.模型示例

2.代码实验（C1_W1_Lab03_Model_Representation）

(1).工具使用

(2).问题描述-房价预测

(3).输入数据

(4).绘制数据集坐标点

(5).建模构造函数

二、代价函数（Cost function）

1.解释一下概念

2.衡量一条直线与训练数据的拟合程度

3.代价函数实验(C1_W1_Lab04_Cost_function_Soln)

(1)引入工具包

(2)输入训练数据

(3)定义计算代价的代价函数

(4)绘制代价函数图

(5)总结

---

在本实验中，你将了解线性回归模型如何在代码中定义，并通过图表观察模型对给定w和b值的数据拟合程度。此外，你还可以尝试不同的w和b值，以检验是否能提升数据拟合效果。

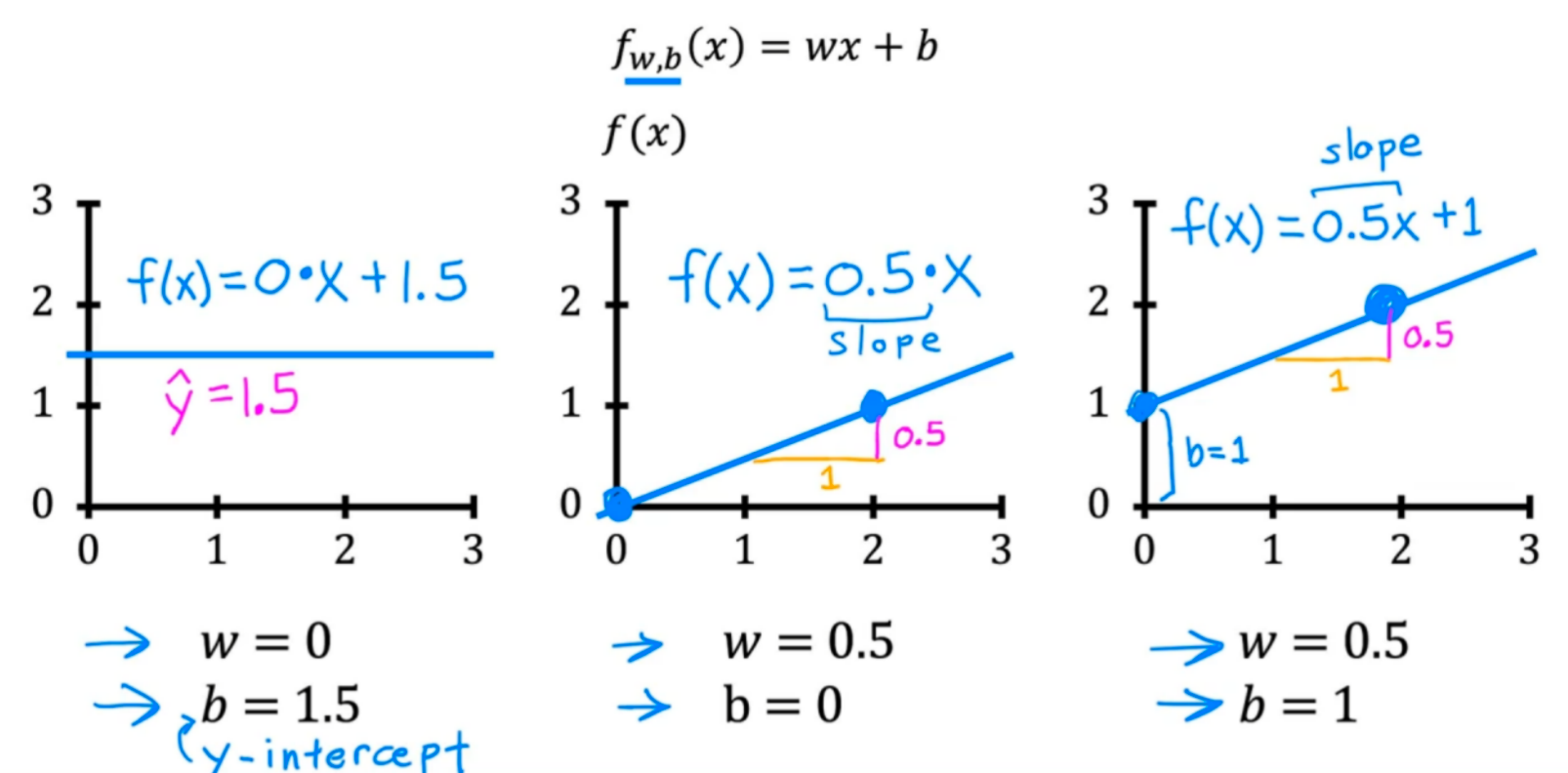
一、线性回归

1.模型示例

首先要有一些数据来训练我们的线性回归函数。

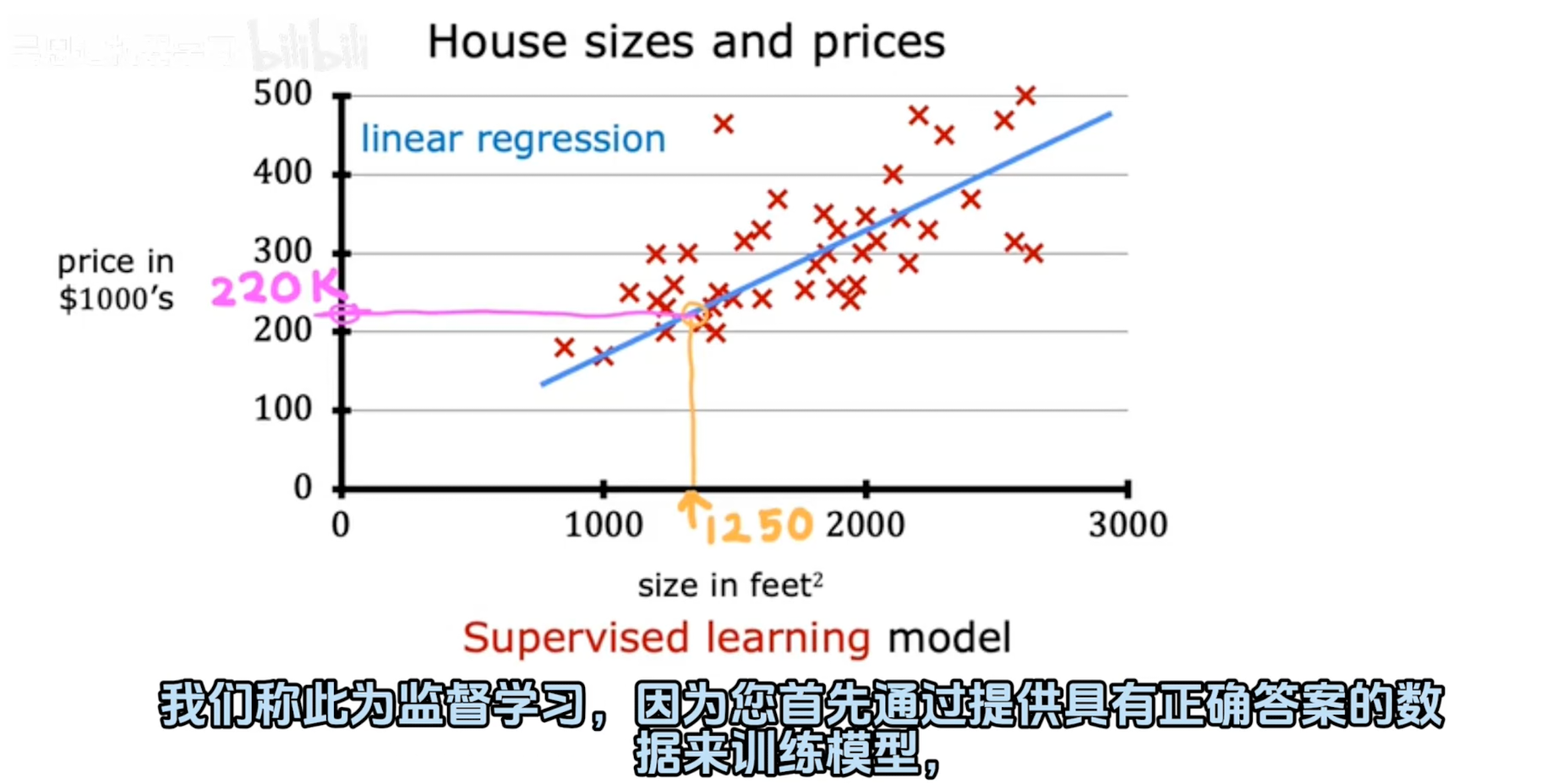
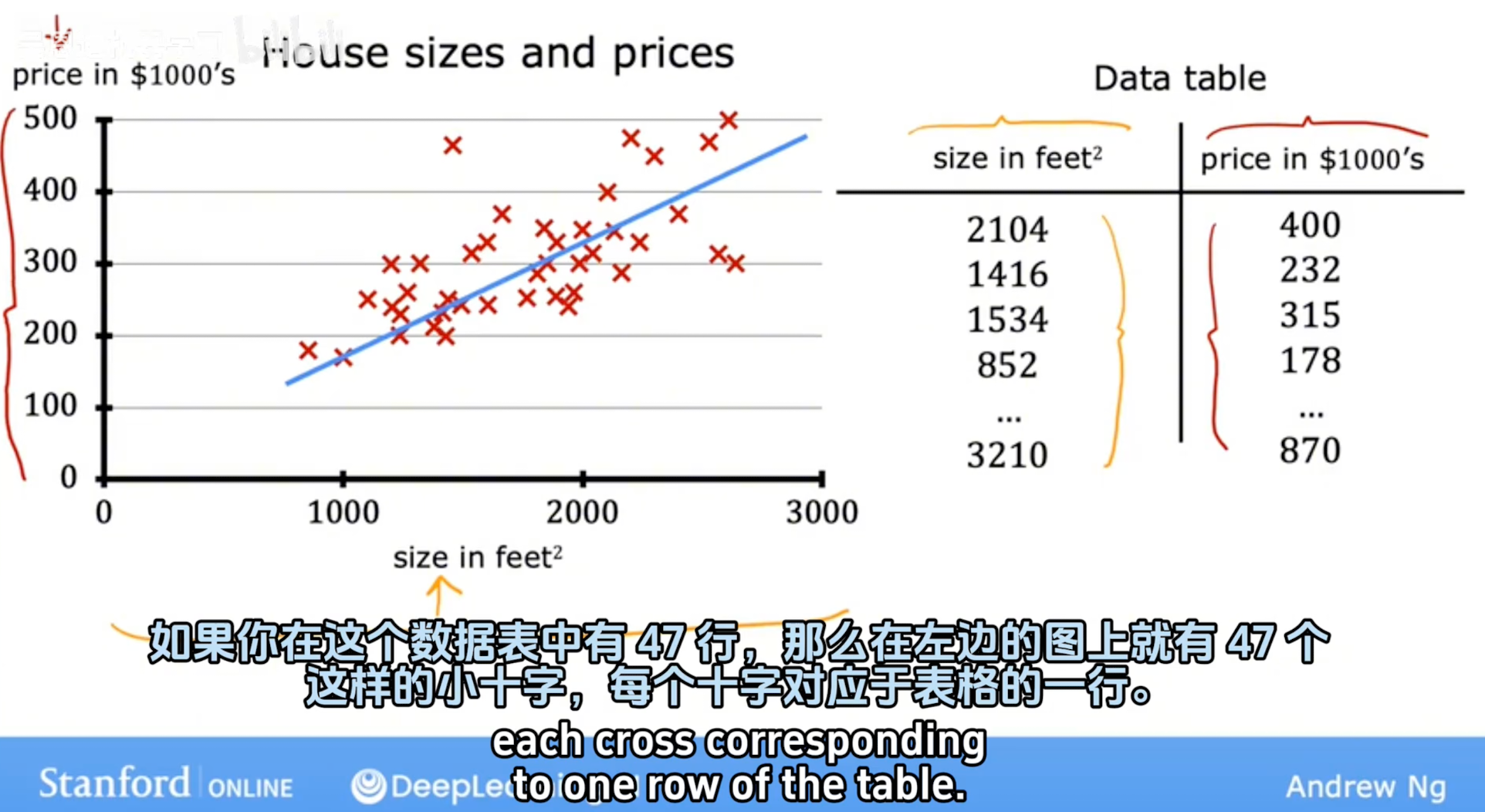
数据集：根据下面的数据集，经过一定的学习算法得到线性回归函数

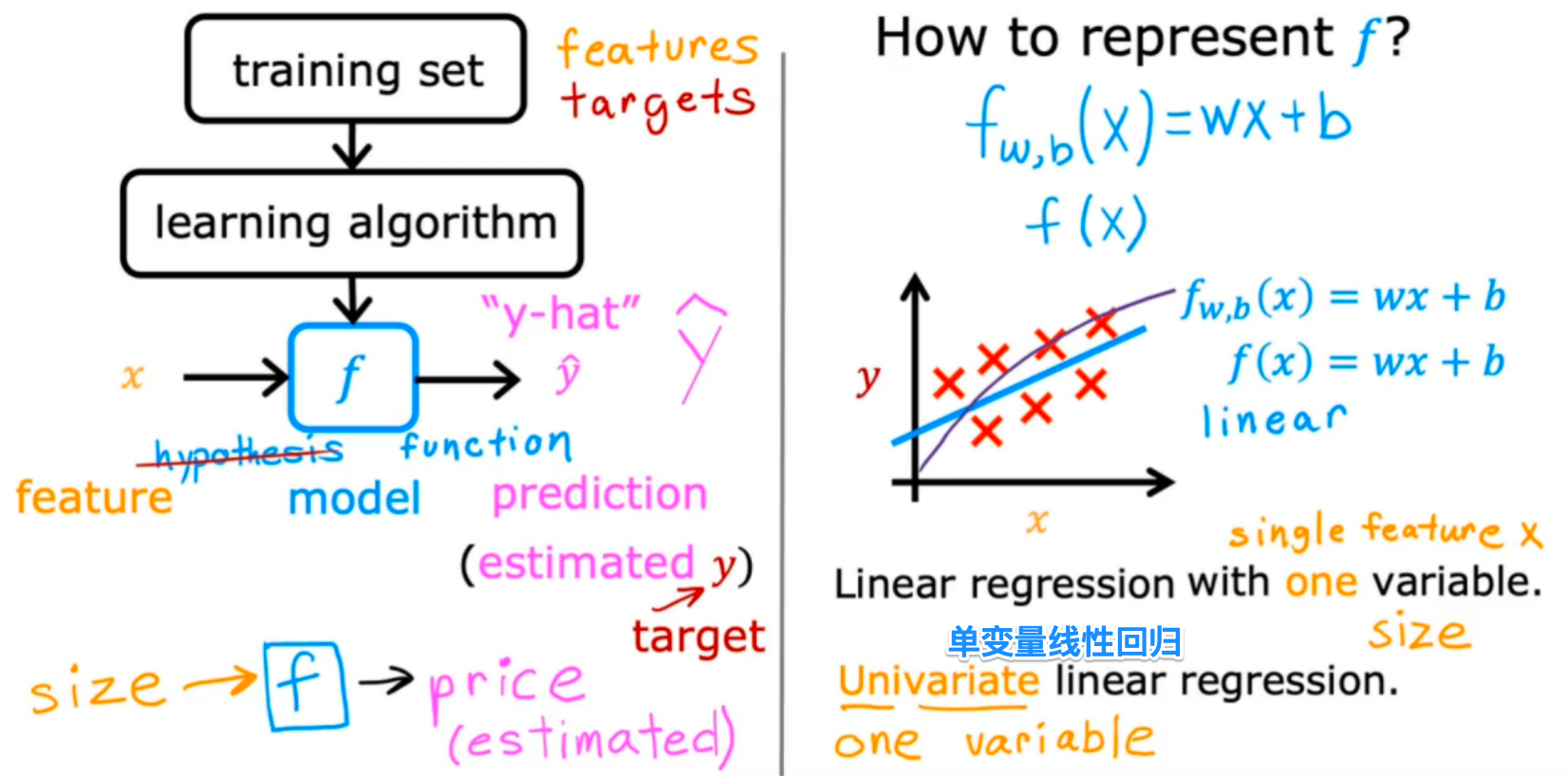
2.代码实验（C1_W1_Lab03_Model_Representation）

(1).工具使用

numpy：用于科学计算的库

matplotlib：绘制图像的库

//引入工具
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')

(2).问题描述-房价预测

这个实验将使用一个只有两个数据点的简单数据集——1000平方英尺的房子以30万美元的价格出售，2000平方英尺的房子以50万美元的价格出售。这两点将构成我们的数据集或训练集。在这个实验里，尺寸的单位是1000平方英尺，价格的单位是1000美元。

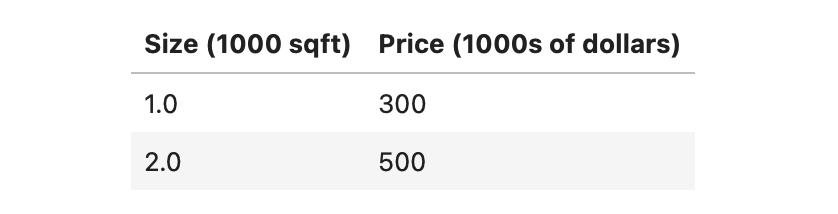
(3).输入数据

# x_train is the input variable (size in 1000 square feet)
# y_train is the target (price in 1000s of dollars)
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
print(f"x_train = {x_train}")
print(f"y_train = {y_train}")

用 m 表示训练样本的数量。Numpy数组有一个 .shape 参数。x_train.shape返回一个python元组，每个元组对应一个维度。x_train.shape[0]是数组的长度和示例的数量，如下代码：

# m is the number of training examples
print(f"x_train.shape: {x_train.shape}")
m = x_train.shape[0]
print(f"Number of training examples is: {m}")

(4).绘制数据集坐标点

# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.show()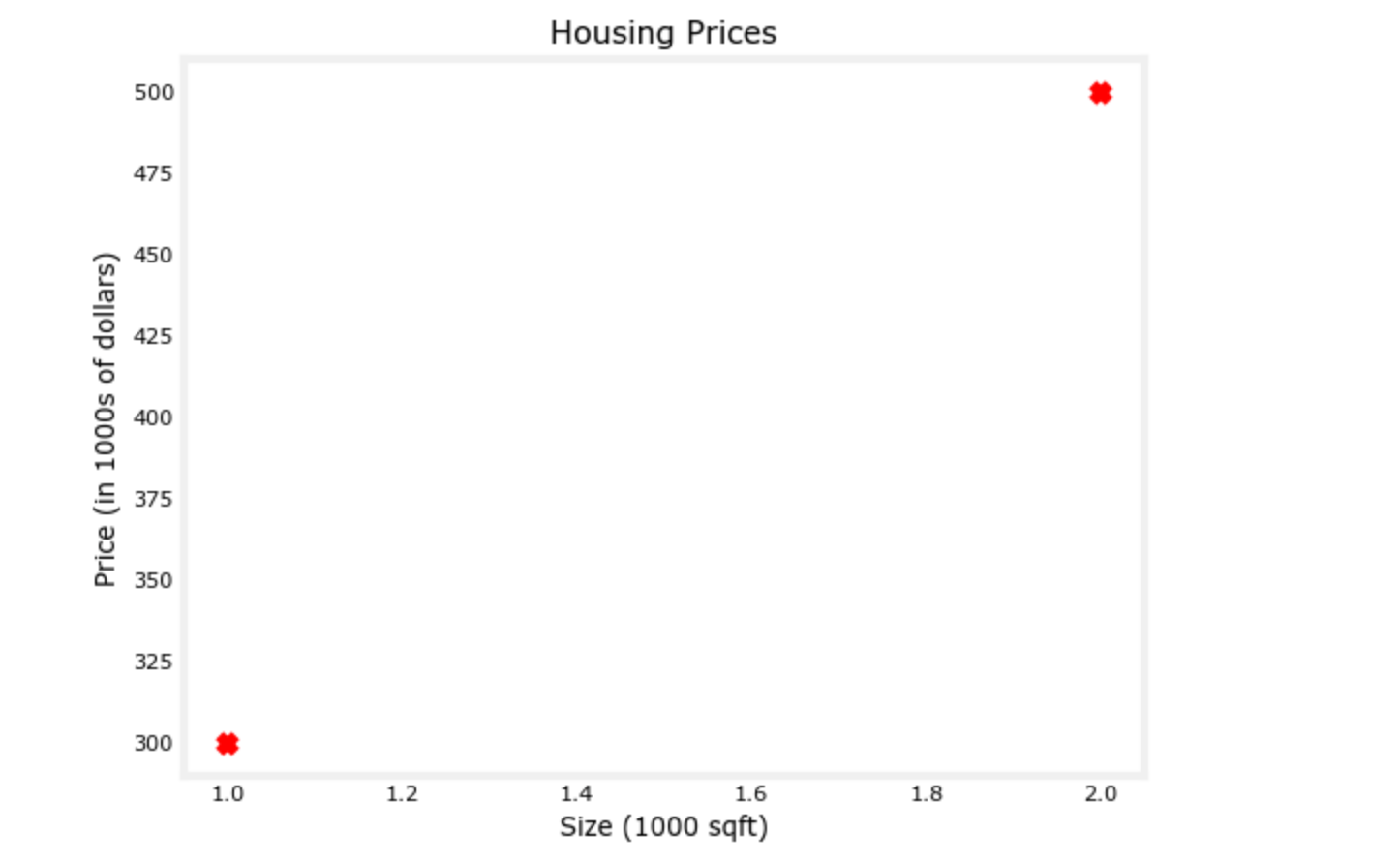

(5).建模构造函数

由问题描述可知该数据集应该是线性模型，f(x)=wx+b

不断的调整w、b，将x代入上式中，判断f(x)是否匹配数据集的y：

//批量计算在当前w、b下f(x)的值
def compute_model_output(x, w, b):
    """
    Computes the prediction of a linear model
    Args:
      x (ndarray (m,)): Data, m examples
      w,b (scalar)    : model parameters  
    Returns
      y (ndarray (m,)): target values
    """
    m = x.shape[0]
    f_wb = np.zeros(m)
    for i in range(m):
        f_wb[i] = w * x[i] + b
        
    return f_wb

可以通过画图的方式直观比较：

tmp_f_wb = compute_model_output(x_train, w, b,)
# Plot our model prediction
plt.plot(x_train, tmp_f_wb, c='b',label='Our Prediction')
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r',label='Actual Values')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.legend()
plt.show()

下图是当w=200，b=100时的图像

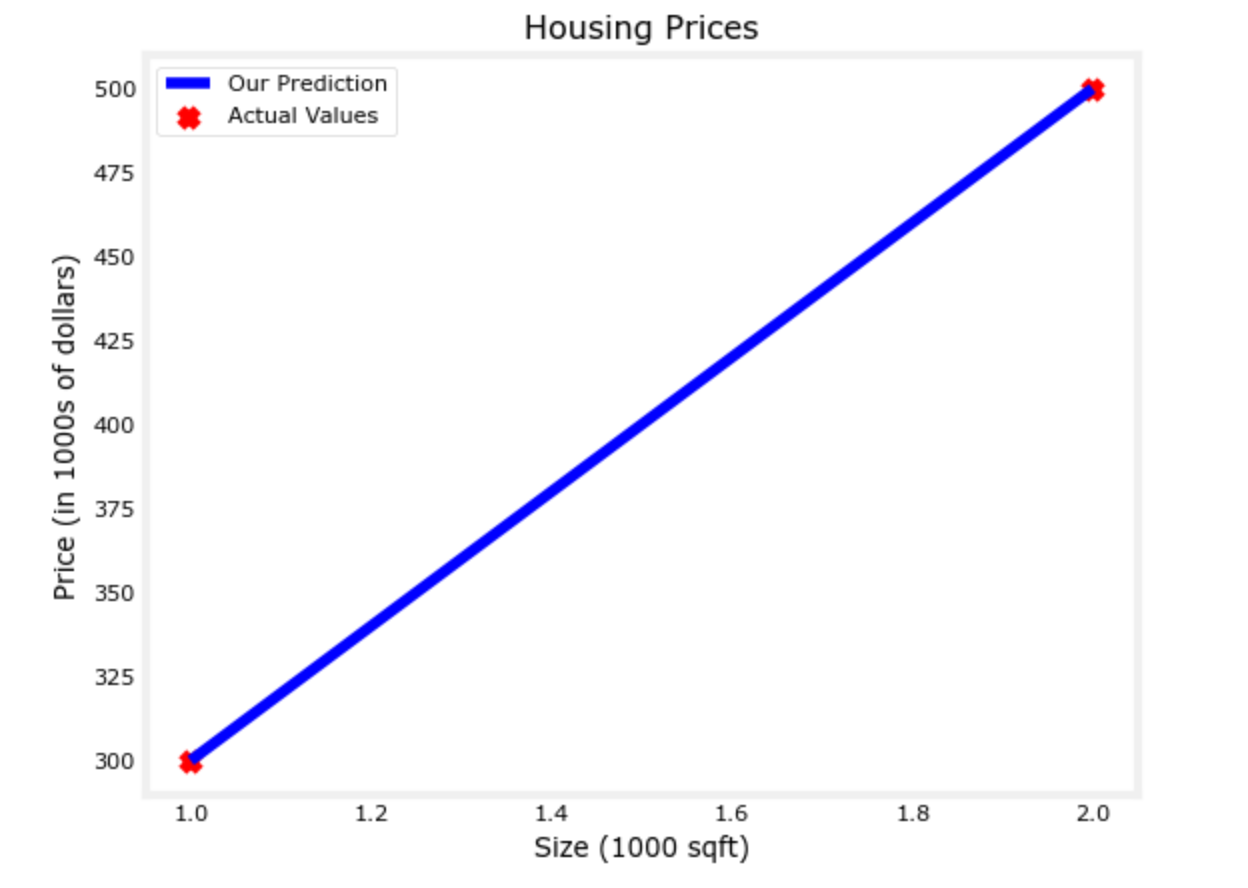
两个数据点均在f(x)=200x+100这条直线上，可以以此来对 新的x 做出预测：

w = 200                         
b = 100    
x_i = 1.2
cost_1200sqft = w * x_i + b    
print(f"${cost_1200sqft:.0f} thousand dollars”)
//输出结果：$340 thousand dollars

二、代价函数（Cost function）

1.解释一下概念

    在机器学习特别是监督学习中，代价函数（Cost Function）是一个关键的概念。它衡量了模型预测结果与实际标签之间的差异或误差。目标是通过优化代价函数来找到最佳的模型参数。

    常见的代价函数有：（这里只是先举出例子了解一下，具体应用后面再说）

        (1). 均方误差（Mean Squared Error, MSE）：适用于回归问题，计算每个样本预测值和真实值之差的平方的平均。

        (2). 交叉熵损失（Cross-Entropy Loss, CEL）：用于分类问题，特别是多类别的softmax分类。它衡量了模型预测的概率分布与实际标签概率分布之间的差异。

        (3). Huber 损失（Huber Loss）：介于均方误差和绝对值误差之间，对于异常值更加鲁棒。

    在优化过程中，我们会不断地调整模型参数来减小代价函数的值。通过最小化代价函数，我们期望找到一个能够在新数据上表现良好的模型。

2.衡量一条直线与训练数据的拟合程度

使用均方误差成本函数

(1)先对简化版本的代价函数（b=0）进行分析：

对于不同的w(斜率)有不同的J(w)，选择最小的J(w)时的w即为最优的线性回归模型参数，图示如下

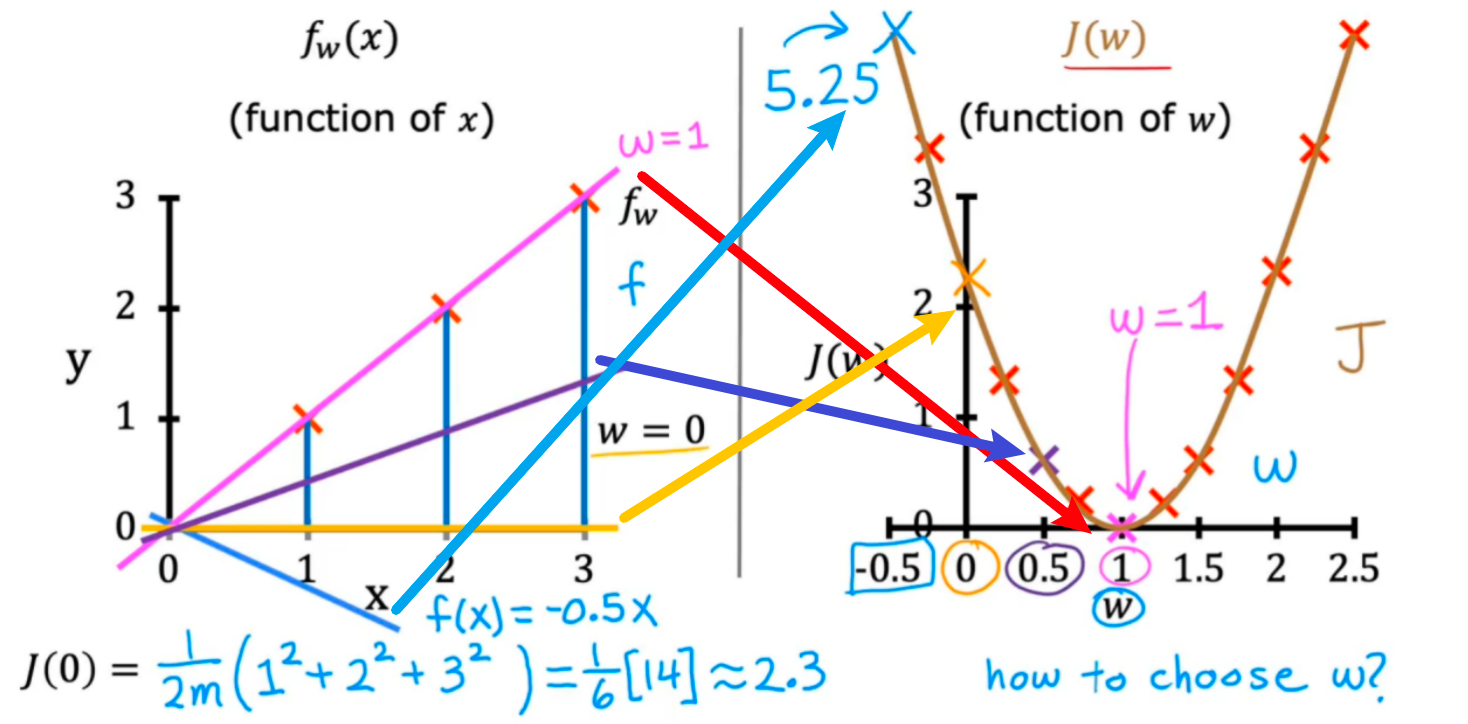
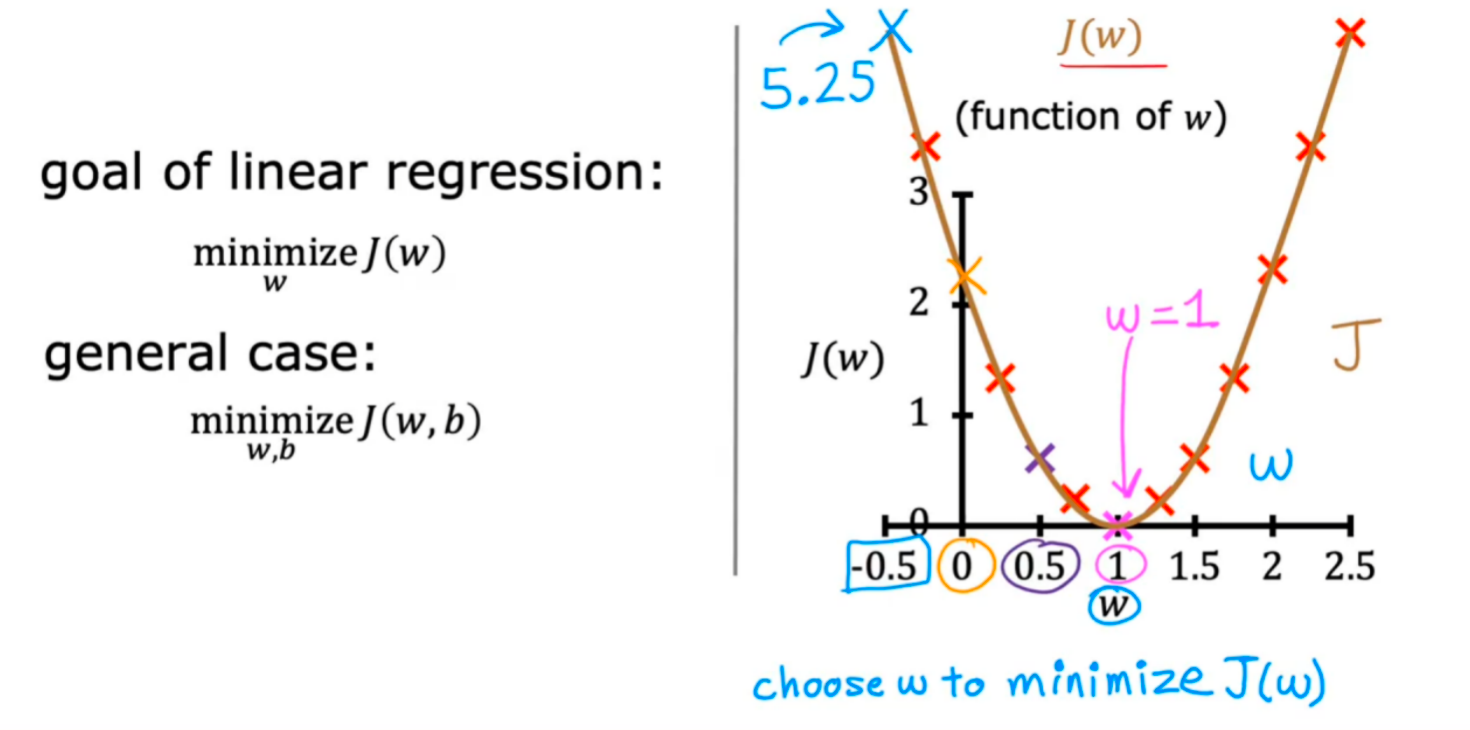
因此，构造线性回归模型的问题就变成了寻找让误差最小的w和b参数

(2)当扩展到一般的回归模型，cost function的图像变成了一个曲面( 三维坐标：w、b、J(w,b) )

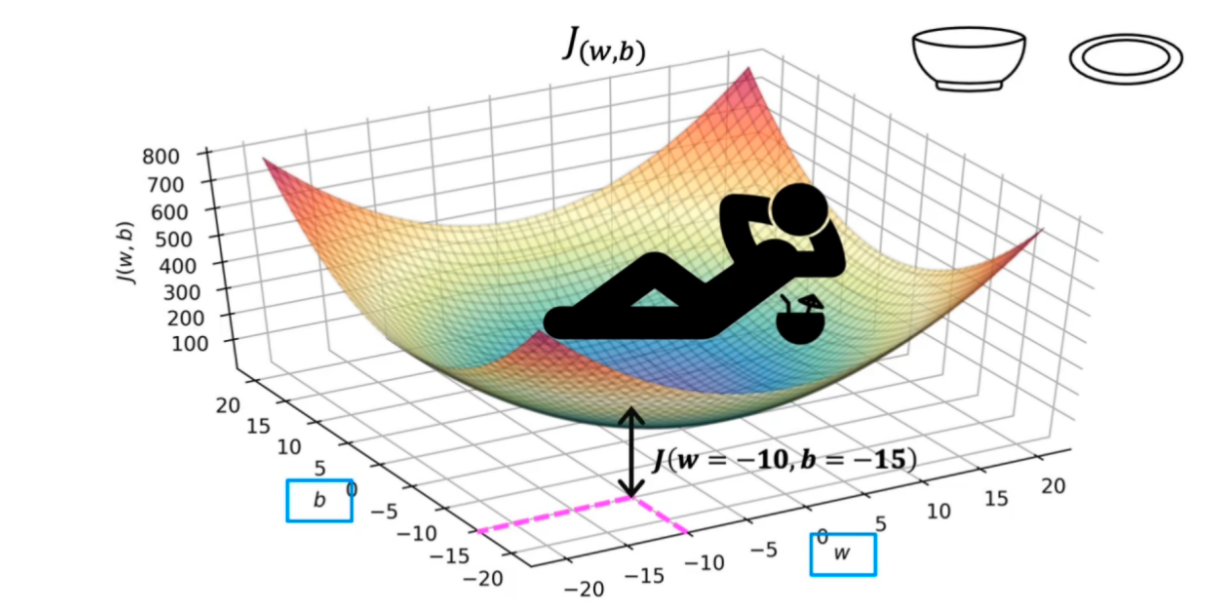
我们同样可以通过数学方法在曲面上找到使代价值J(w,b)最小的参数w和b

往往3D的曲面图会用2D的等高线图来等价表示，用于研究规律：

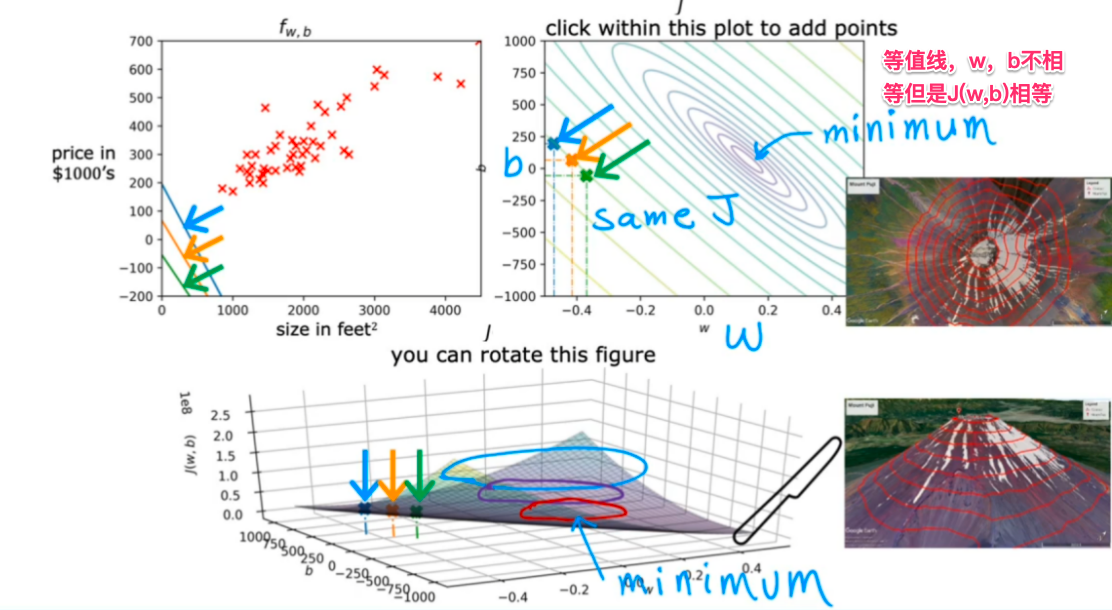
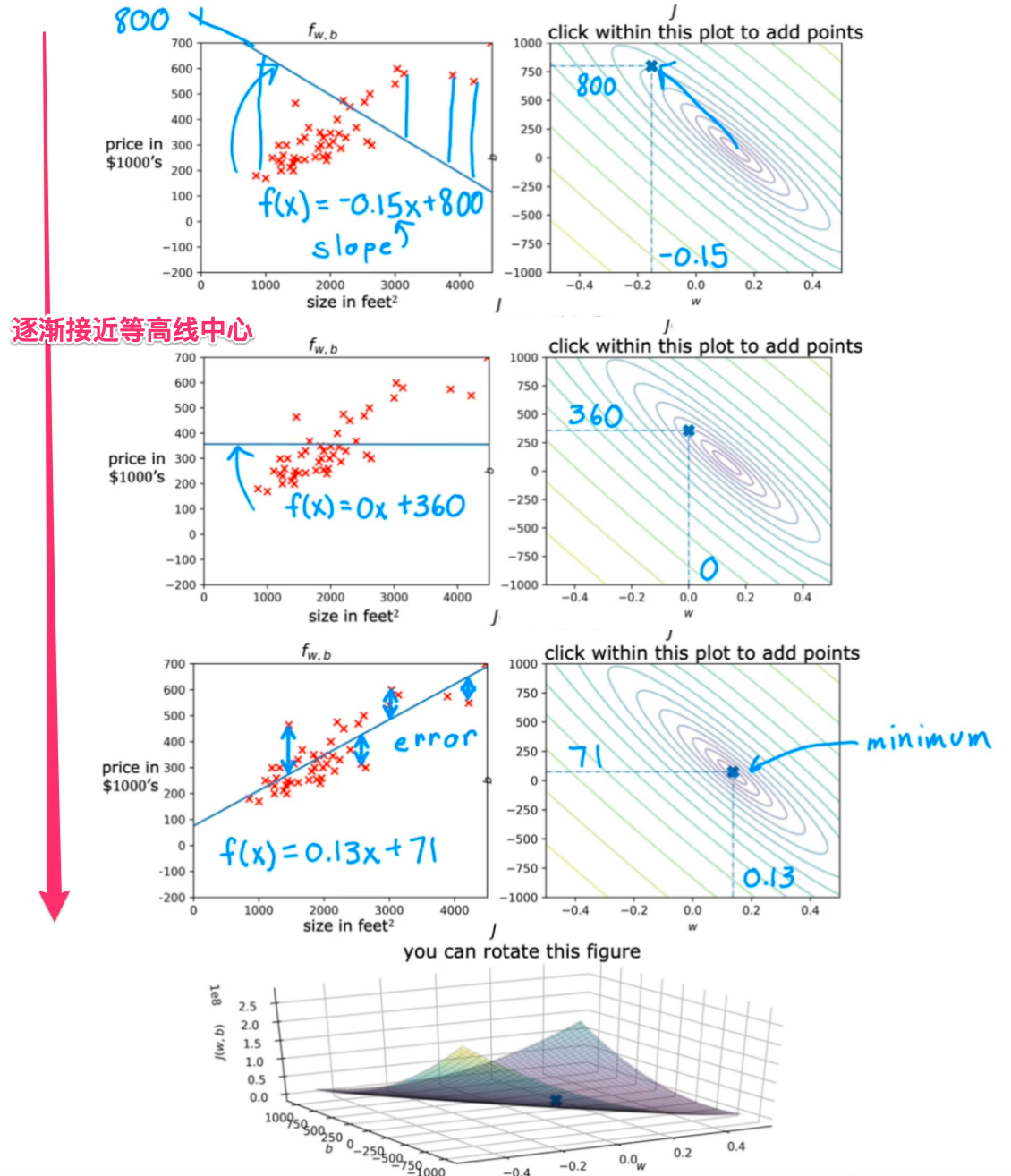
对于不同w、b时，f(x)和J(w,b)的图像对应情况：

3.代价函数实验(C1_W1_Lab04_Cost_function_Soln)

(1)引入工具包

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_uni import plt_intuition, plt_stationary, plt_update_onclick, soup_bowl
plt.style.use('./deeplearning.mplstyle')

发现出现缺少依赖包的情况：

pip install ipympl

重启内核继续执行引入工具包的操作

(2)输入训练数据

x_train = np.array([1.0, 2.0])           #(size in 1000 square feet)
y_train = np.array([300.0, 500.0])           #(price in 1000s of dollars)

(3)定义计算代价的代价函数

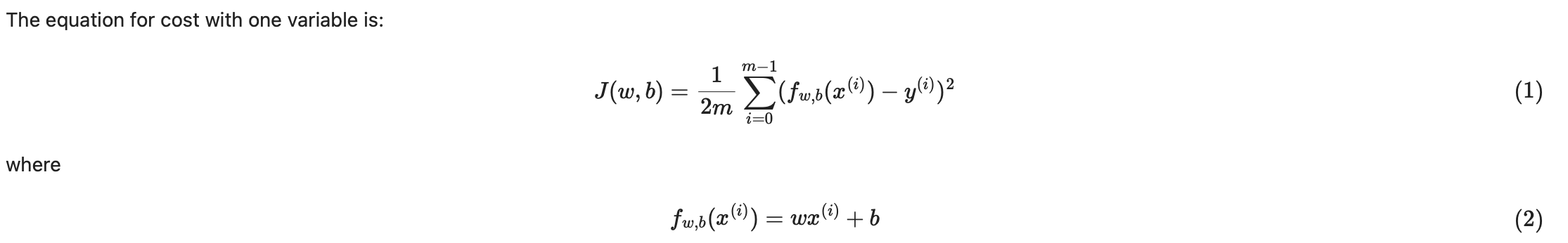
def compute_cost(x, y, w, b): 
    """
    Computes the cost function for linear regression.
    
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    
    Returns
        total_cost (float): The cost of using w,b as the parameters for linear regression
               to fit the data points in x and y
    """
    # number of training examples
    m = x.shape[0] 
    
    cost_sum = 0 
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  


    return total_cost

(4)绘制代价函数图

①由数据可知，拟合最好的回归模型b=100，这里先看一下固定b=100时，w变化时，J(w)的变化情况

//绘制w-J(w)变化图，函数具体原码看代码包：当前课程资源：week1/work/lab_utils_uni.py
plt_intuition(x_train,y_train)

如果绘图时遇到这个问题：Failed to load model class 'VBoxModel' from module '@jupyter-widgets/controls’

需要安装 widgets 依赖：

pip install ipywidgets

如果还是不好使可能是版本问题，将依赖组件升级一下

pip install -U jupyterlab ipywidgets jupyterlab_widgets

w=130时的误差：6125

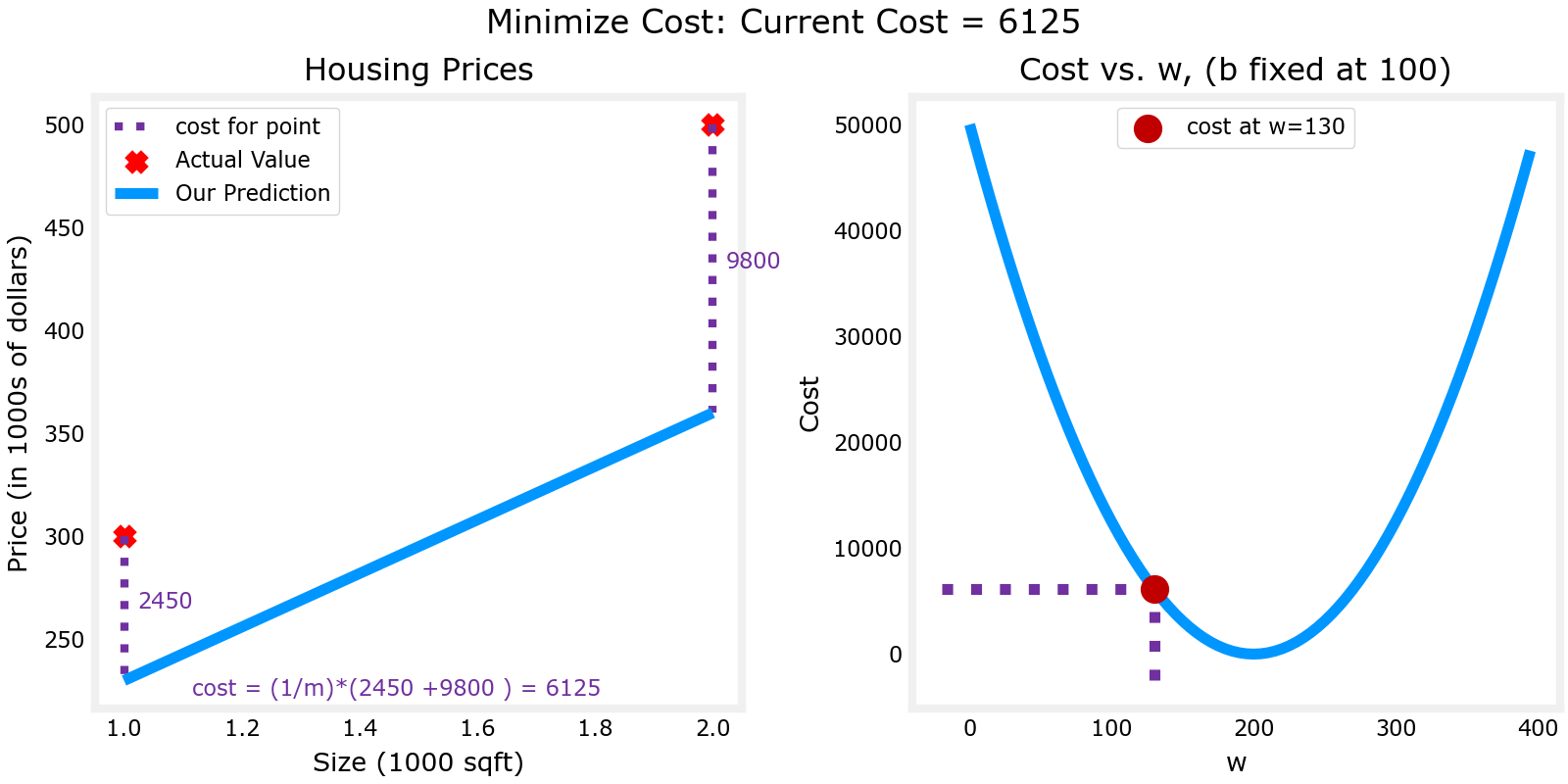
w=200时，误差为0

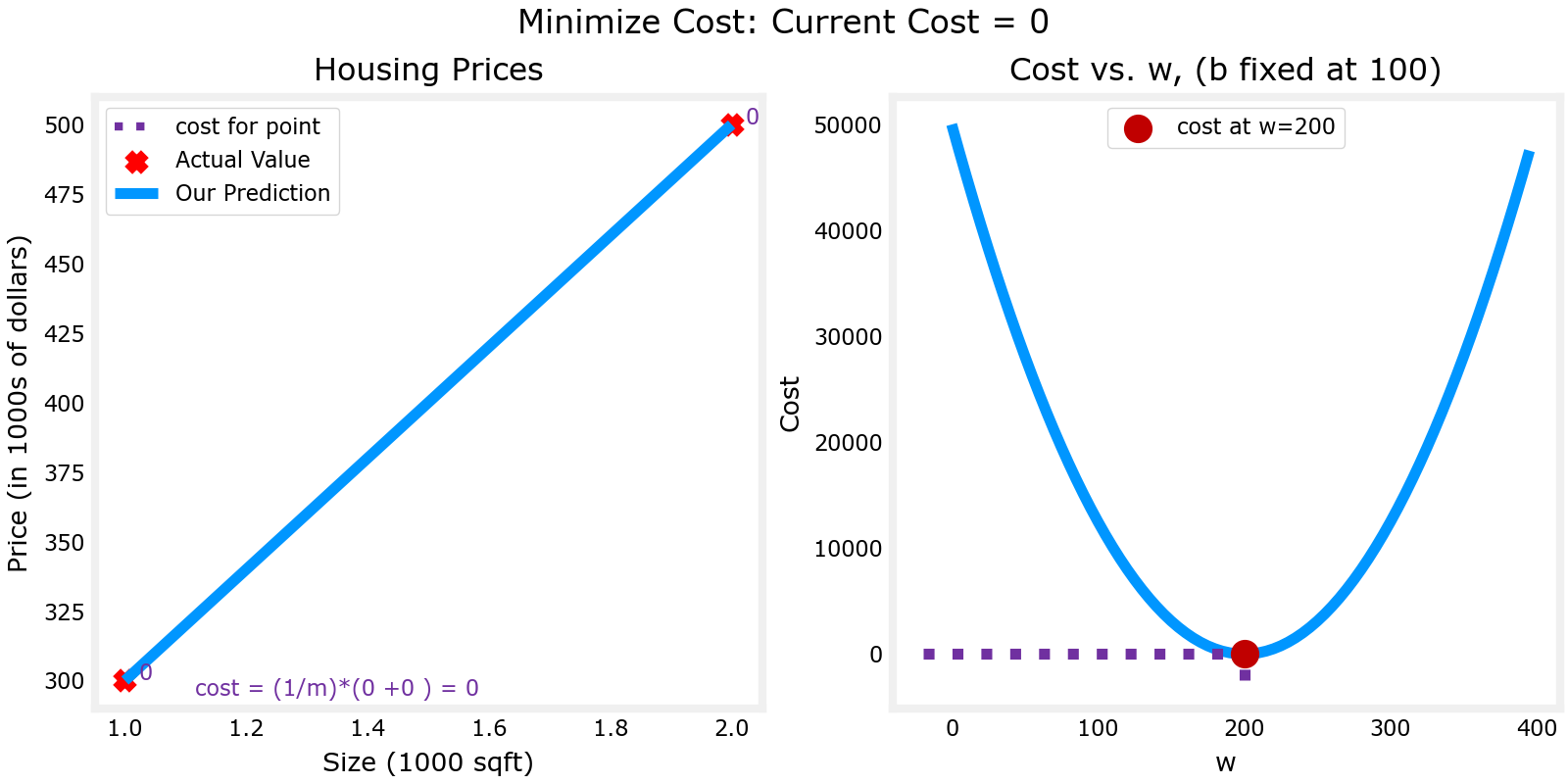
//绘图-三维图
plt.close('all') 
fig, ax, dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)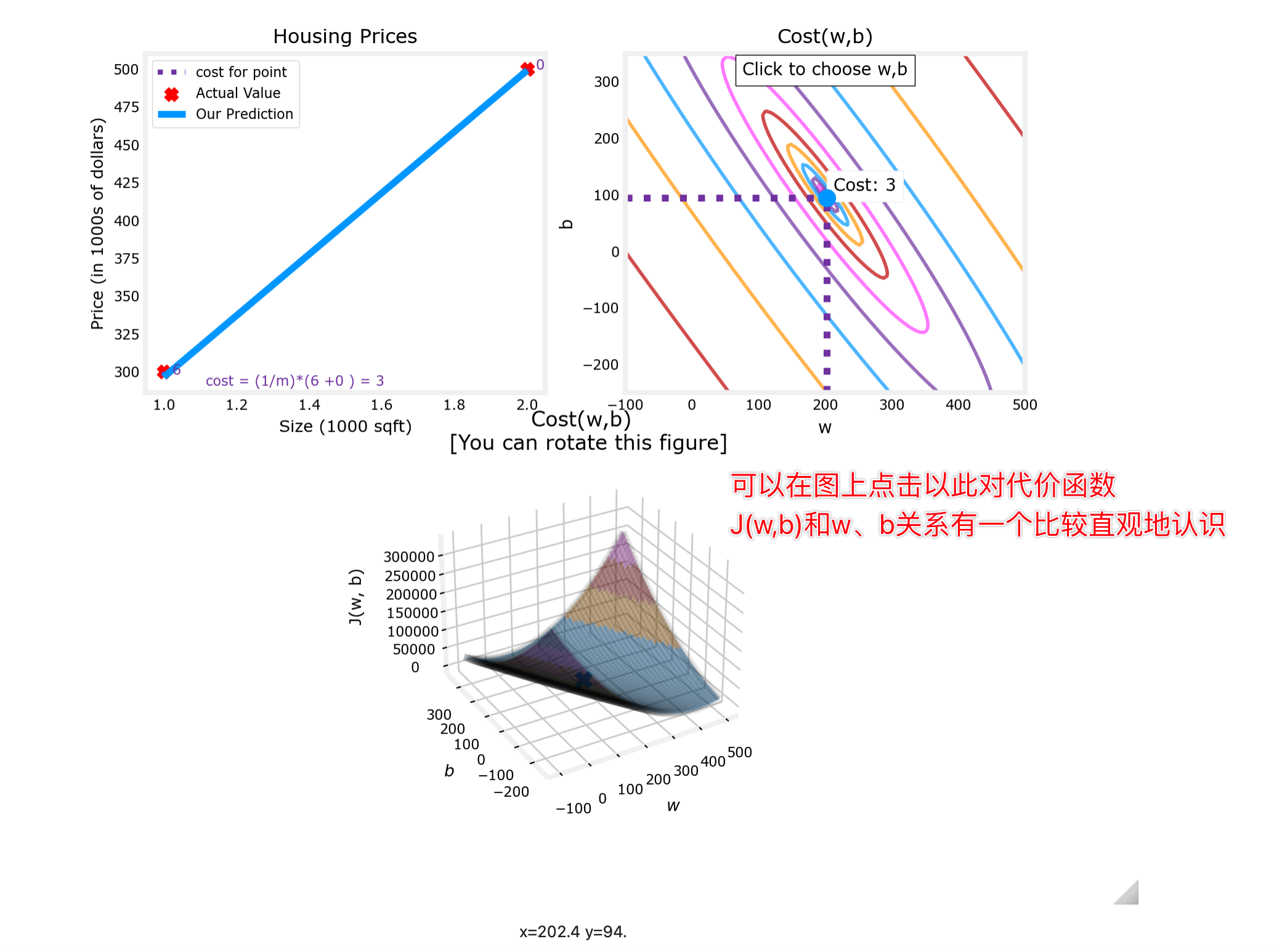

②对于更大规模的数据集，我们不能通过看来发现合适的w和b

所以我们使用3D的图来显示w、b、J(w,b)之间的关系：

//数据集
x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
y_train = np.array([250, 300, 480,  430,   630, 730,])

//绘图
plt.close('all') 
fig, ax, dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)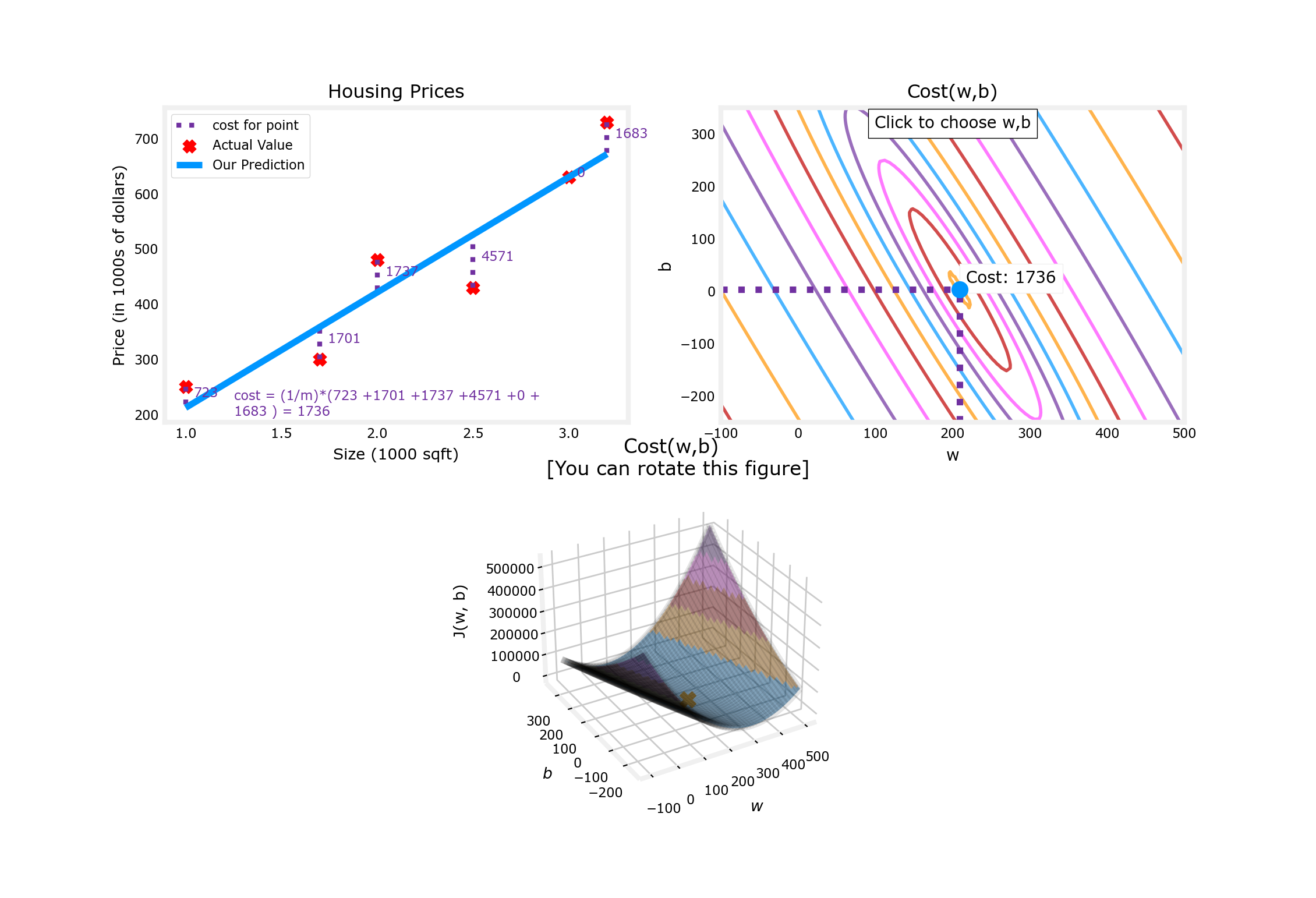

(5)总结

成本函数对损失进行平方，这一事实确保了“误差曲面”是凸的，就像一个汤碗。它总是有一个可以通过在所有维度上遵循梯度达到的最小值。

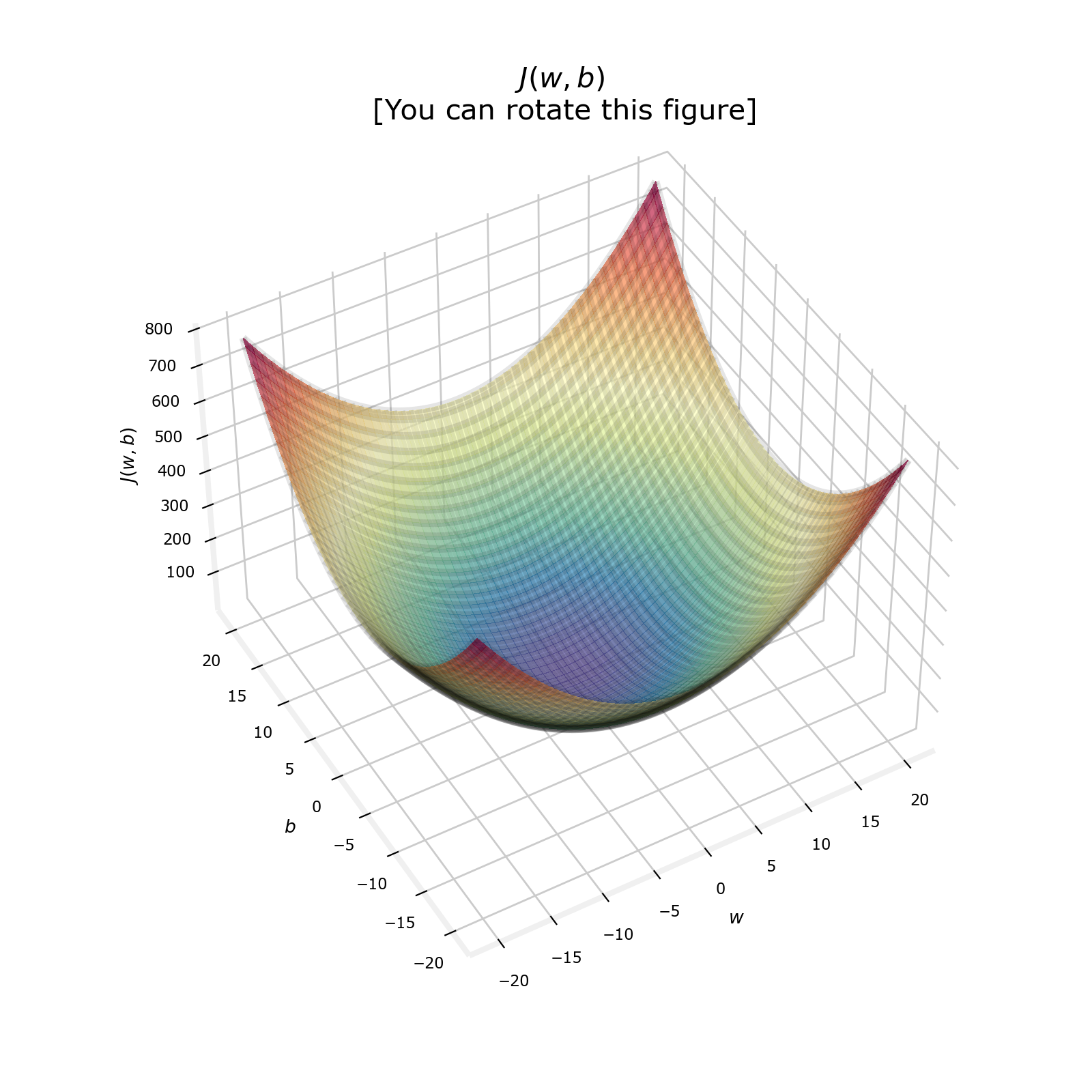
下一章将开始学习梯度下降法，可以解决寻找使J(w,b)最小的w和b。