独家首发 | 基于 KAN、KAN卷积的轴承故障诊断模型

往期精彩内容：

Python-凯斯西储大学（CWRU）轴承数据解读与分类处理

Python轴承故障诊断入门教学-CSDN博客

Python轴承故障诊断 (13)基于故障信号特征提取的超强机器学习识别模型-CSDN博客

Python轴承故障诊断 (14)高创新故障识别模型-CSDN博客

Python轴承故障诊断 (15)基于CNN-Transformer的一维故障信号识别模型-CSDN博客

轴承故障全家桶更新 | 基于时频图像的分类算法-CSDN博客

Python轴承故障诊断 (16)高创新故障识别模型（二）-CSDN博客

Python轴承故障诊断 (17)基于TCN-CNN并行的一维故障信号识别模型_pytorch使用tcn网络进行故障诊断 csdn-CSDN博客

独家原创 | SCI 1区高创新轴承故障诊断模型！-CSDN博客

Python轴承故障诊断 (18)基于CNN-TCN-Attention的创新诊断模型-CSDN博客

Python轴承故障诊断 (20)高创新故障识别模型（三）-CSDN博客

注意力魔改 | 超强轴承故障诊断模型！-CSDN博客

Python轴承故障诊断 (21)基于VMD-CNN-BiTCN的创新诊断模型-CSDN博客

基于k-NN + GCN的轴承故障诊断模型-CSDN博客

火遍AI圈的最新论文 KAN: Kolmogorov-Arnold Network 大家应该听说过了，那咱们基于 KAN 的轴承故障诊断还会远吗？发论文的核心点就是紧跟前沿，跟着大牛喝口汤！这一轮热点来袭，有论文需求的同学可要把握住机会哟！

在 KAN 和 CKAN ( Convolutional Kolmogorov-Arnold Network ) 的基础上，我们提供了五种轴承故障诊断模型的对比

MLP: 两层 MLP (第一层神经元 64，第二层神经元32)
KAN: 两层优化后的 KANLinear (第一层神经元 64，第二层神经元32)
CNN-1D: 3 层的普通 1D 卷积池化层 + 1 层线性层
CNN-1D-KAN: 3 层的普通 1D 卷积池化层 + 1 层 KANLinear
KAN-Conv: 2 层的KANConv + 1 层线性层

五种模型实验效果对比如下：（注意！此代码也比较容易和我们往期推出的模型进行融合，在这个基础上，进一步增加一些实验或者模块，就可以直接拿去发文章！！！）

从对比实验可以看出, 在轴承故障诊断任务中：

KAN的准确率要优于 MLP，我们可以进一步尝试在常规模型的最后一层线性层都替换为 KAN 层来进行对比；KAN 卷积比常规卷积准确率有略微的提升！

相关学习资料和完整的数据、五种分类代码如下：

点击文末阅读原文，获取代码

● 数据集：CWRU西储大学轴承数据集

● 环境框架：python 3.9 pytorch 2.0 及其以上版本均可运行

● 输出结果：训练过程损失、准确率曲线图、测试集准确率报告、混淆矩阵

● 使用对象：论文需求、毕业设计需求者

● 代码保证：代码注释详细、即拿即可跑通。

前言

本文基于凯斯西储大学（CWRU）轴承数据，先经过数据预处理进行数据集的制作和加载，最后通过Pytorch实现优化的KAN模型和KAN卷积模型对故障数据的分类。凯斯西储大学轴承数据的详细介绍可以参考下文：

Python-凯斯西储大学（CWRU）轴承数据解读与分类处理_cwru数据集-CSDN博客

1 KAN 网络介绍

1.1 KAN 网络三大特征

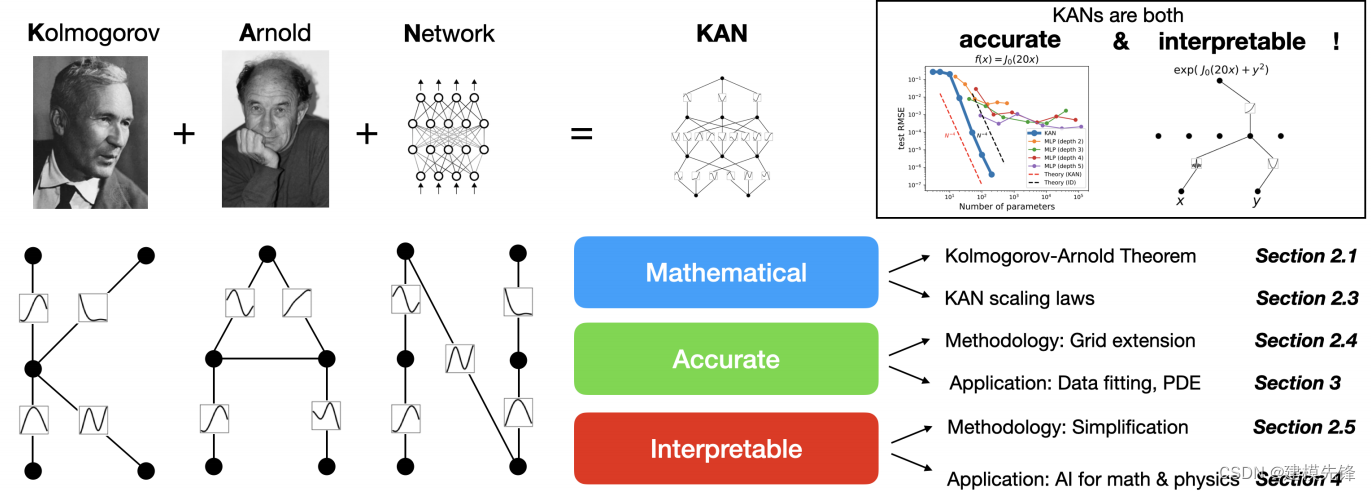
数学上有据可依
准确性高
可解释性强

1.2 传统 MLP 的本质

多层感知机（MLPs），也称为全连接前馈神经网络，是深度学习模型的基础构建块。MLPs 的重要性不言而喻，因为它们是机器学习中用于逼近非线性函数的默认模型，其表达能力由普适逼近定理保证。

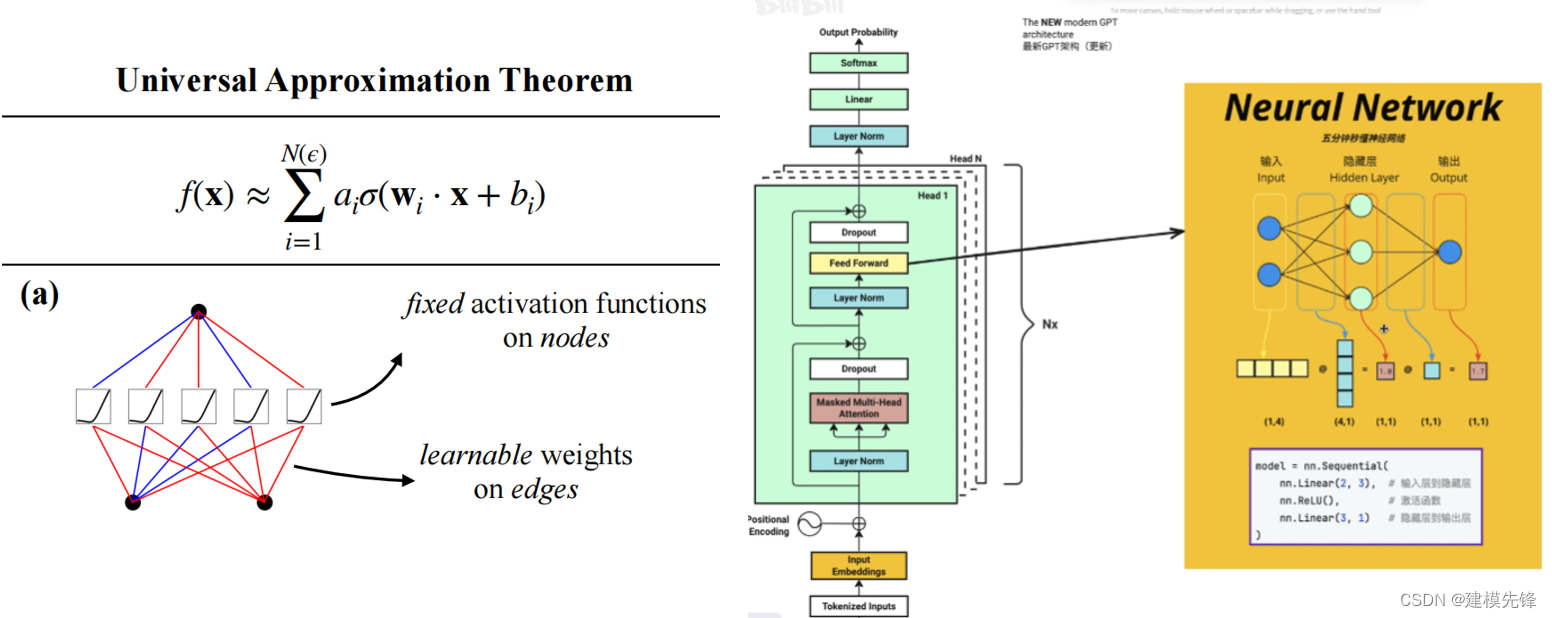
（1）容易产生梯度消失和梯度爆炸：

梯度消失：梯度趋近于零，网络权重无法更新或更新的很微小，网络训练再久也不会有效果；
梯度爆炸：梯度呈指数级增长，变的非常大，然后导致网络权重的大幅更新，使网络变得不稳定。

（2）参数效率低：

MLP 通常使用全连接层，意味着每层的每个神经元都与前一层的所有神经元相连接，导致参数数量迅速增加，尤其是对输入维度很高的数据；这不仅增加了计算负担，也增加了模型过拟合的风险。

（3）可解释性差：

尽管 MLPs 的使用普遍，但它们有着显著的缺点。例如，在Transformer中，MLPs 几乎消耗所有非嵌入参数，并且通常在没有后续分析工具的情况下（相对于注意力层）不太可解释。其可解释性比较差，和一个黑盒模型一样，无法探究是怎么进行学习的。

1.3 MLP 与 KAN 对比

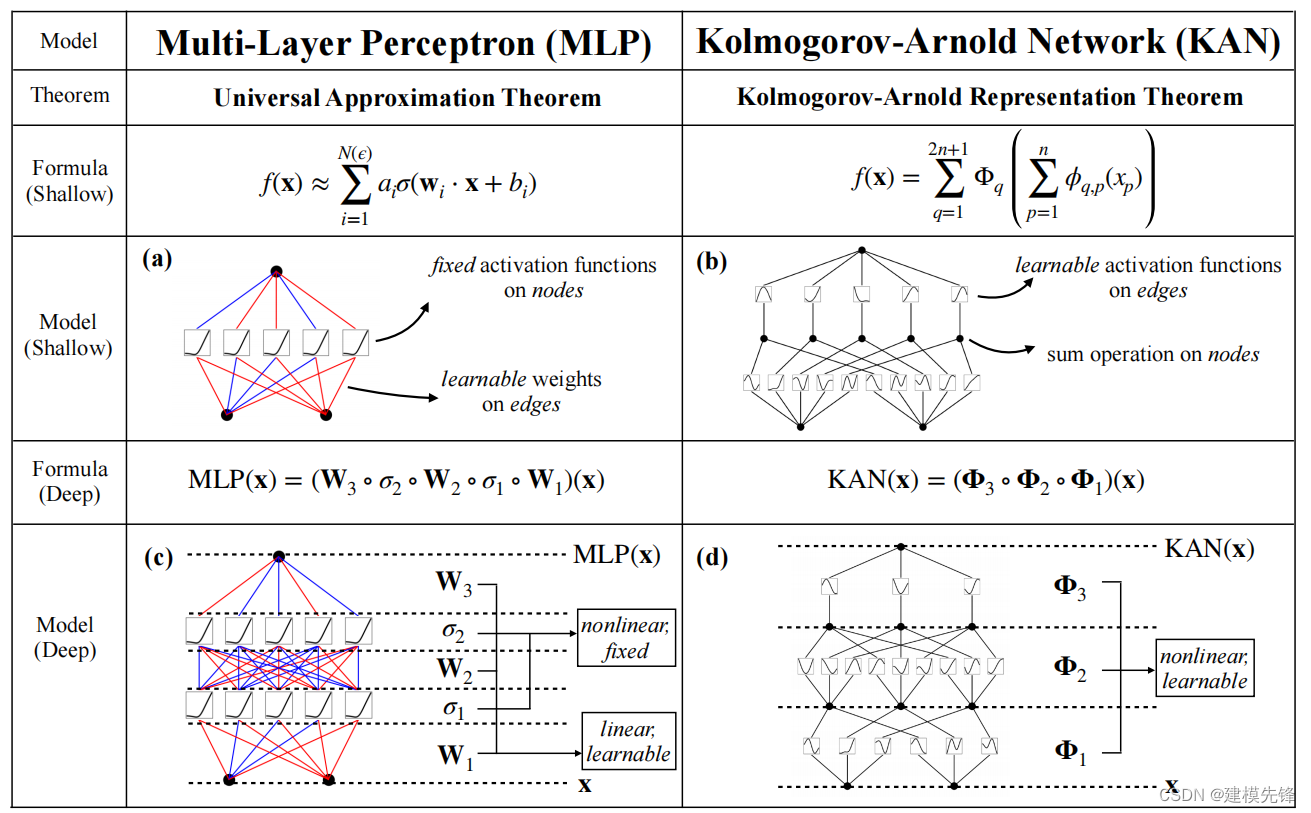
（1）Kolmogorov-Arnold 定理：

任何一个多变量连续函数都可以表示为一些单变量函数的组合！（

在数学的视角，任何问题的核心都是在拟合函数）

（2）激活函数可学习的：

神经网络中每一层的输入输出都是一个线性求和的过程，所以如果没有激活函数，那么无论你构造的神经网络多么复杂，有多少层，最后的输出都是输入的线性组合，纯粹的线性组合并不能够解决更为复杂的问题。而引入激活函数之后，我们会发现常见的激活函数都是非线性的，使得神经网络可以逼近其他的任何非线性函数。与MLP不同激活函数固定，而 KAN 激活函数可学习的, 是可变的！

MLP: 激活函数固定, 输入先相加再激活
KAN: 激活函数可学习的，输入先激活再相加

（3）样条函数：

KAN 中的每层非线性函数 Ф 都采用同样的函数结构，只是用不同的参数来控制其形状，文章选择了数值分析中的样条函数 spline ,样条理论是函数逼近的有力工具。

样条函数是由多个多项式片段组成的函数，每个片段在相邻节点之间定义。这些片段在节点处连接，以确保整体函数的光滑性。

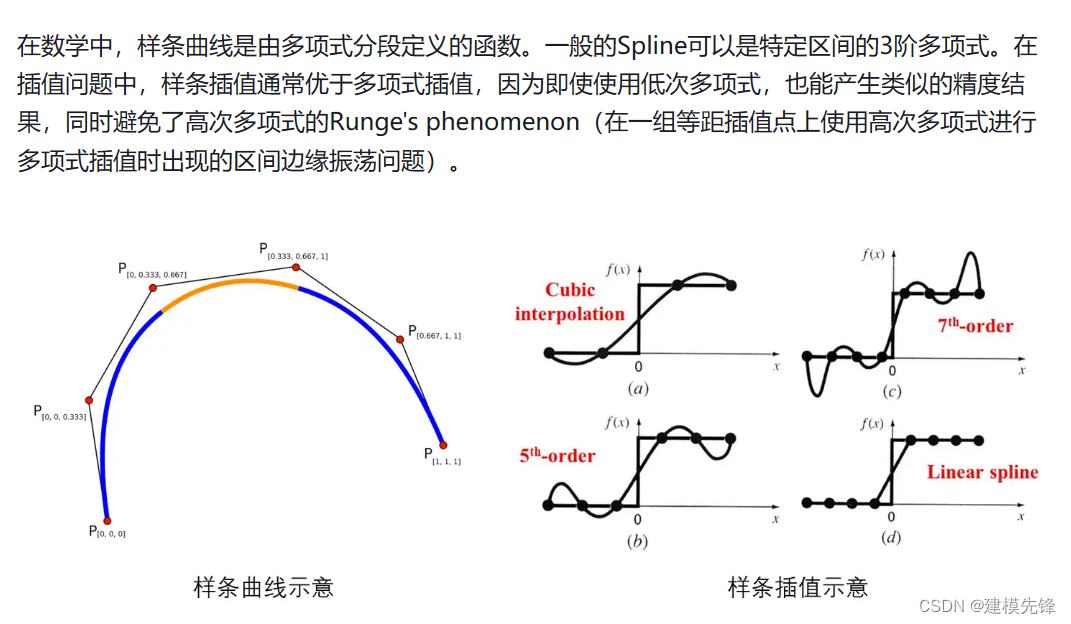
b样条曲线有一个优势就是有明显的几何意义。通过砍角算法(嵌套的线性插值)可以方便的进行曲线的细分、导矢计算、曲线分割、逼近(消去节点)，不仅可以方便的进行各种操作，而且精度比采用幂基函数的多项式样条高。

（4）MLP 与 KAN 对比：

MPL 是固定的非线性激活 + 线性参数学习，KAN 则是直接对参数化的非线性激活函数的学习。KAN 实现了使用更少的节点，更小的网络，来实现同样的效果，甚至更优的效果！

1.4 KAN 执行过程

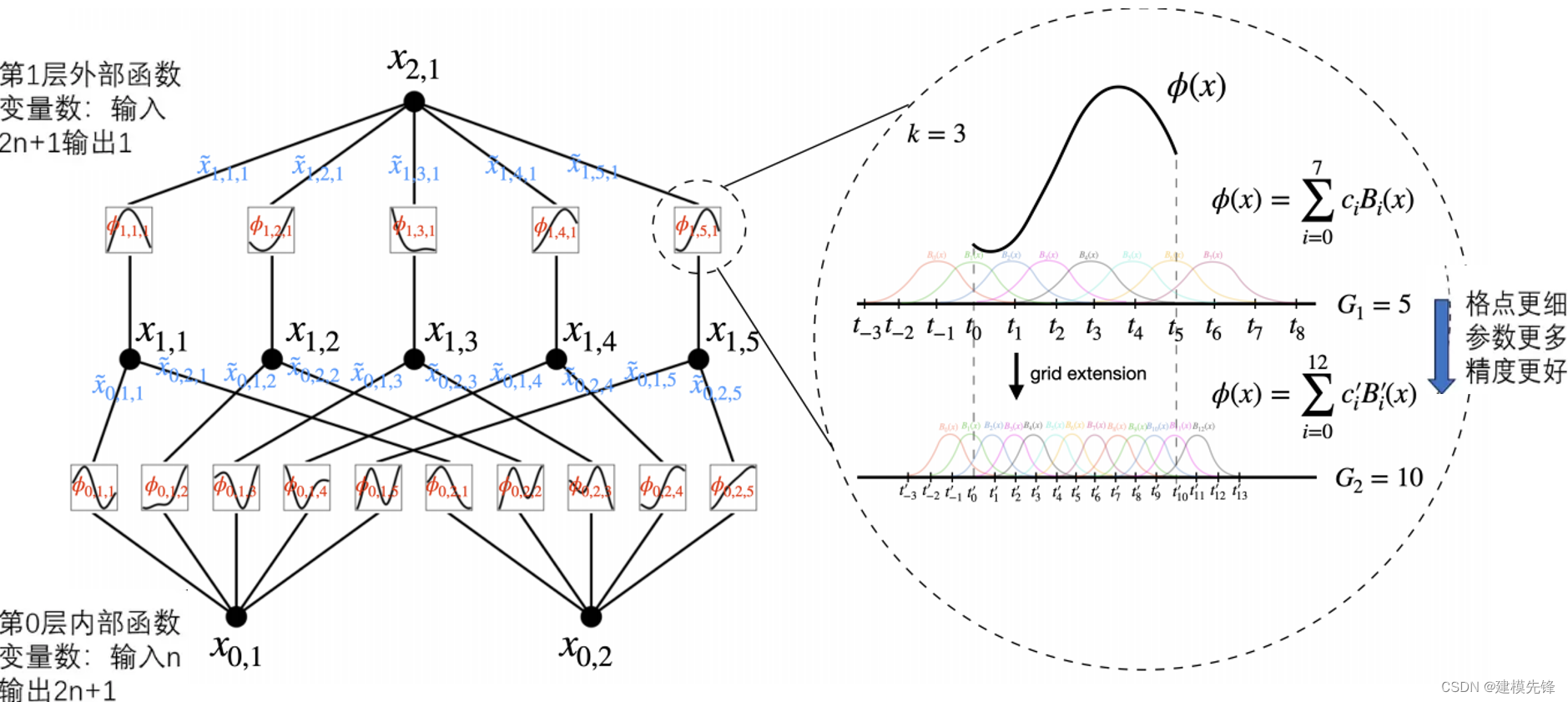
1.5 可解释性

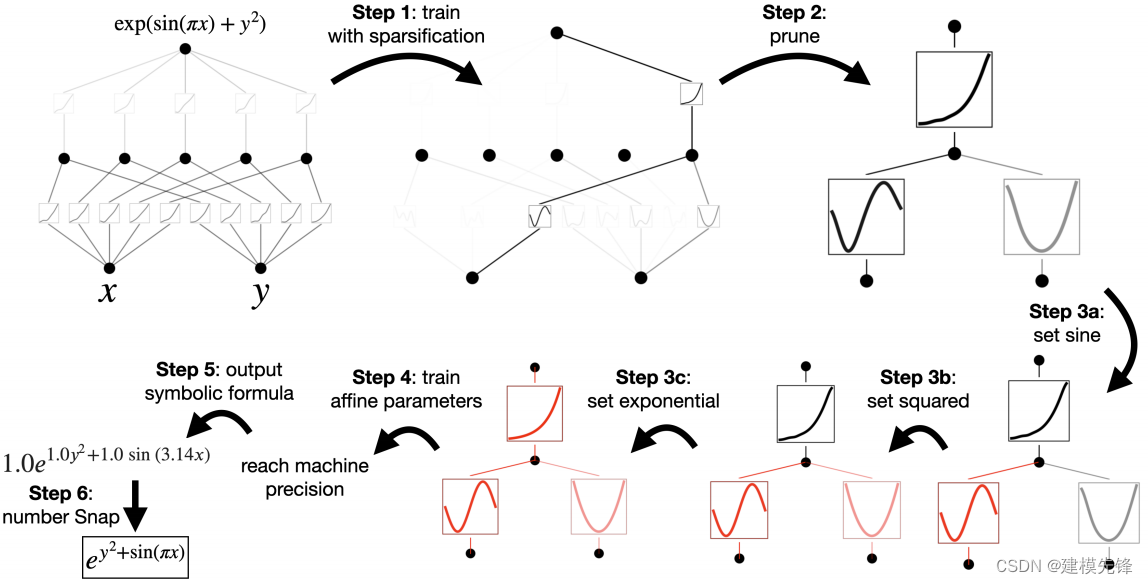
运行代码文件中的 hellokan.ipynb 实现上述可视化过程

2 KAN 卷积（CKAN）

2.1 CKAN

最近，有研究者将 KAN 创新架构的理念扩展到卷积神经网络，将卷积的经典线性变换更改为每个像素中可学习的非线性激活函数，提出并开源 KAN 卷积（CKAN）

KAN 卷积与卷积非常相似，但不是在内核和图像中相应像素之间应用点积，而是对每个元素应用可学习的非线性激活函数，然后将它们相加。KAN 卷积的内核相当于 4 个输入和 1 个输出神经元的 KAN 线性层。

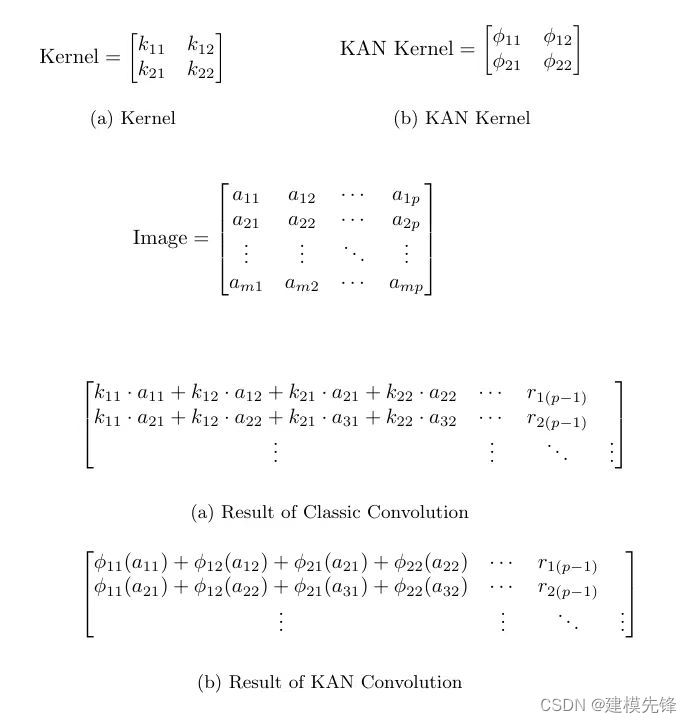
2.2 CKAN 中的参数

假设有一个 KxK 内核，对于该矩阵的每个元素，都有一个 ϕ，其参数计数为：gridsize + 1，ϕ 定义为：

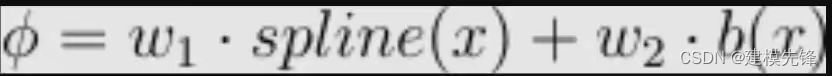
这为激活函数 b 提供了更多的可表达性，线性层的参数计数为 gridsize + 2。因此，KAN 卷积总共有 K^2(gridsize + 2) 个参数，而普通卷积只有 K^2。

3.3 CKAN 在轴承故障诊断中的应用

通过前面的对比实验可以看出，基于 KAN 的卷积网络比传统卷积网络在轴承故障分类任务上效果会好一些，但是训练时间较长。后续可以考虑融合其他模块，做进一步优化；同时基础的 KAN 层完全可以替代分类任务中的全连接层，效果显著，可以在其他数据集上做进一步的对比实验。总的来说，KAN 卷积的实现是一个很有前景的想法，在轴承故障诊断任务上也存在一定的应用前景，值得我们去探索！

3 轴承故障数据的预处理

3.1 导入数据

参考之前的文章，进行故障10分类的预处理，凯斯西储大学轴承数据10分类数据集：

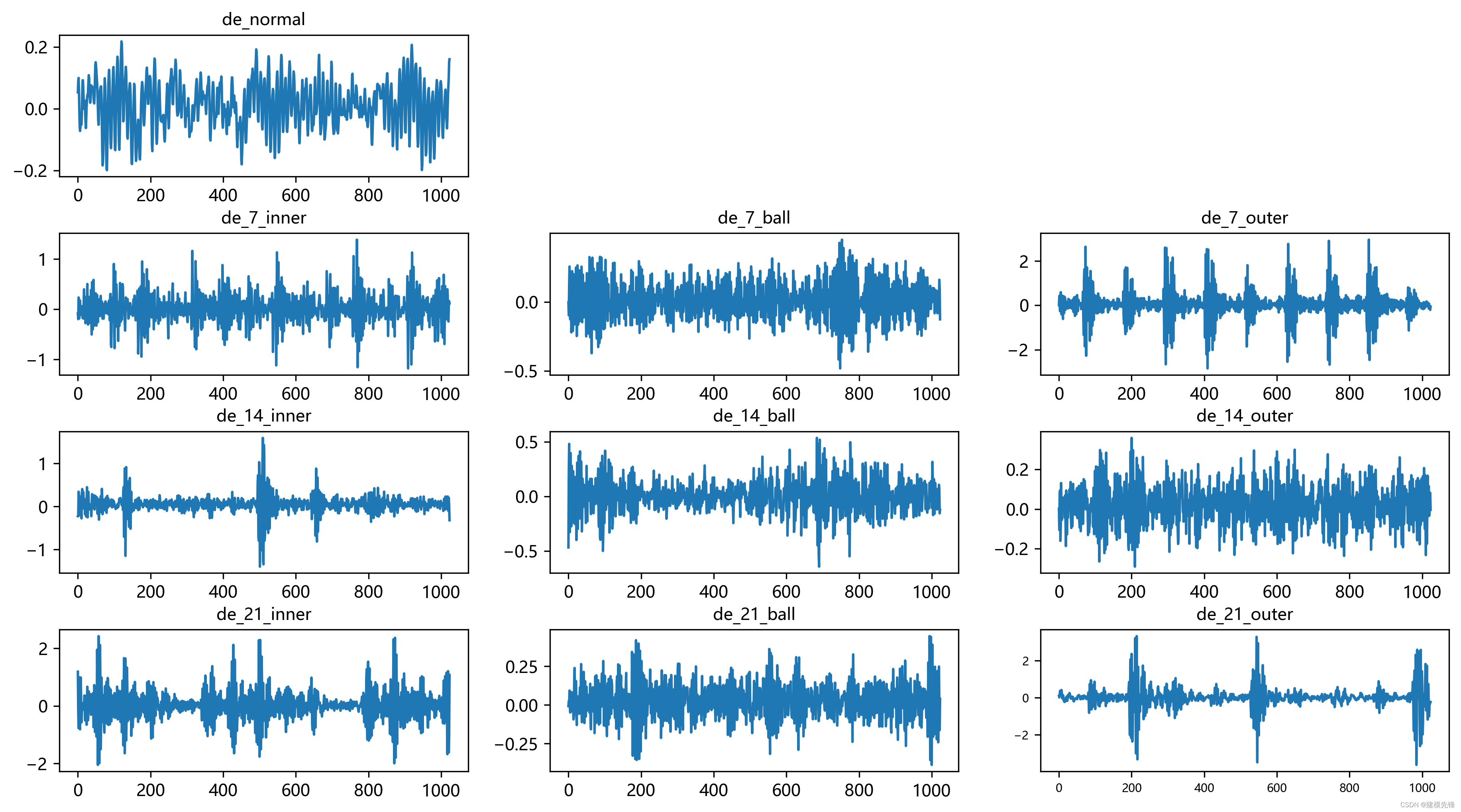
train_set、val_set、test_set 均为按照7：2：1划分训练集、验证集、测试集，最后保存数据

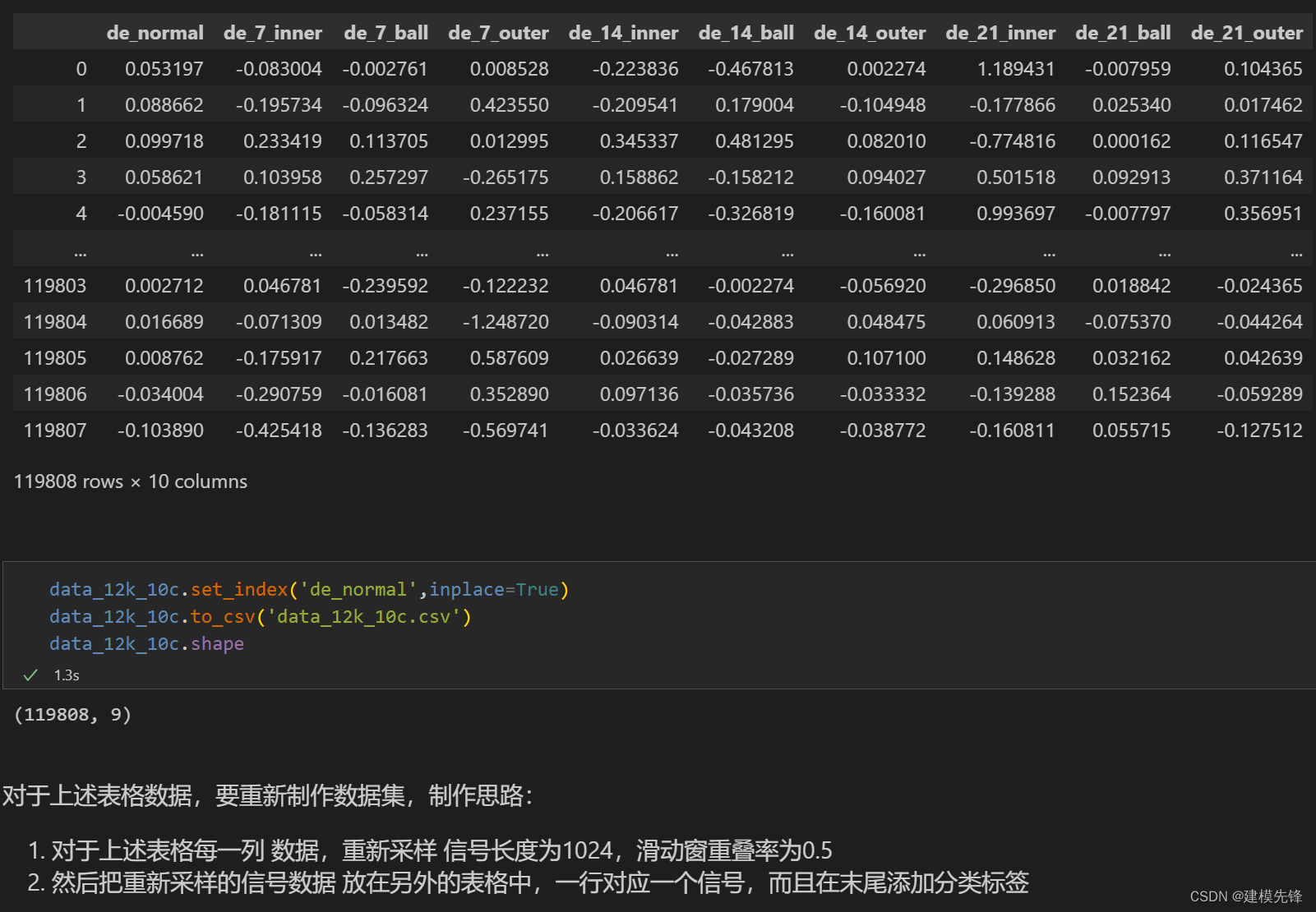
上图是数据的读取形式以及预处理思路

3.2 数据预处理，制作数据集

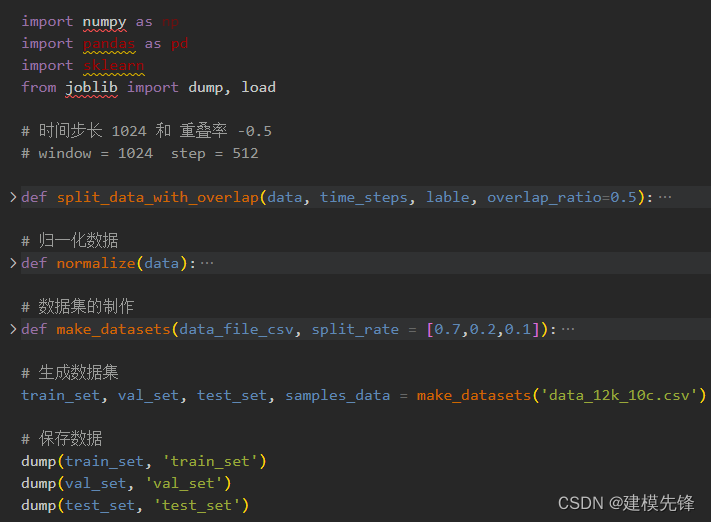
4 基于 Pytorch的 KANConv 的轴承故障诊断

4.1 定义 KANConv 分类网络模型，设置参数，训练模型

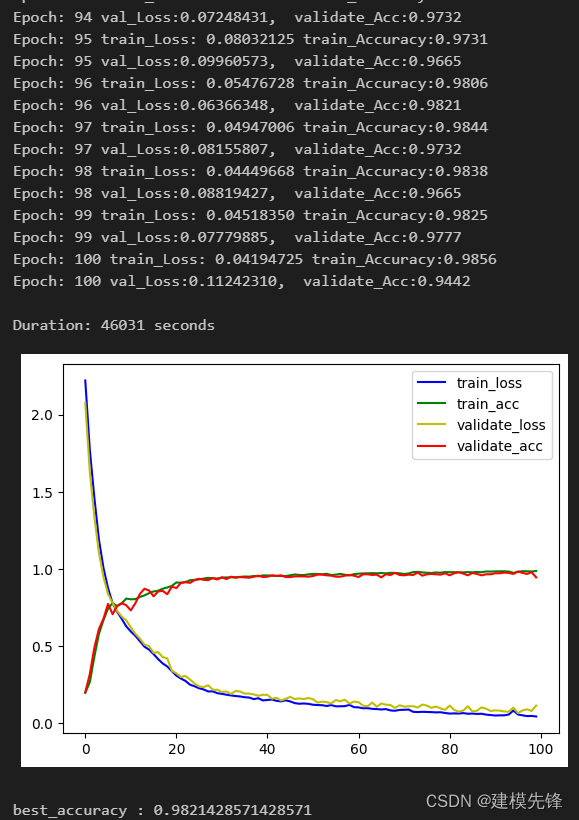
100个epoch，训练集、验证集准确率98%，用改进 KAN 卷积网络分类效果显著，模型能够充分提取轴承故障信号中的故障特征，收敛速度快，性能优越，精度高，效果明显!（代价是运行时间比传统CNN网络要慢）

4.2 模型评估

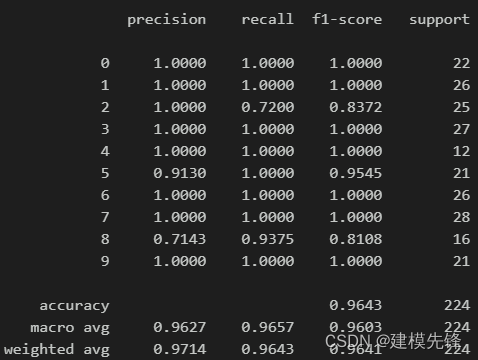
准确率、精确率、召回率、F1 Score

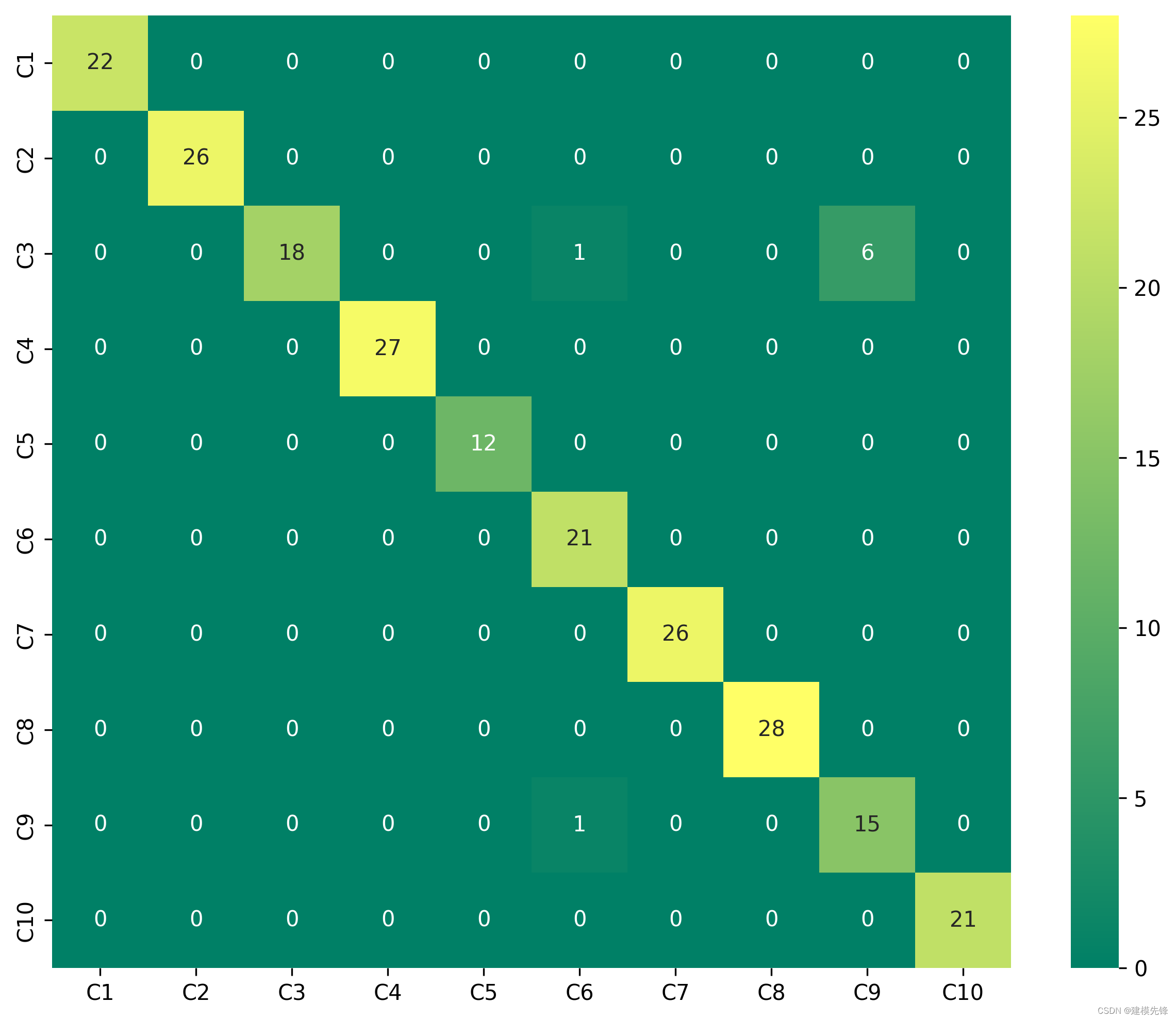
故障十分类混淆矩阵：

代码、数据如下：

对数据集和代码感兴趣的，可以关注最后一行

# 加载数据
import torch
from joblib import dump, load
import torch.utils.data as Data
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
# 参数与配置
torch.manual_seed(100)  # 设置随机种子，以使实验结果具有可重复性
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
 
#代码和数据集：https://mbd.pub/o/bread/ZpaWmpdy