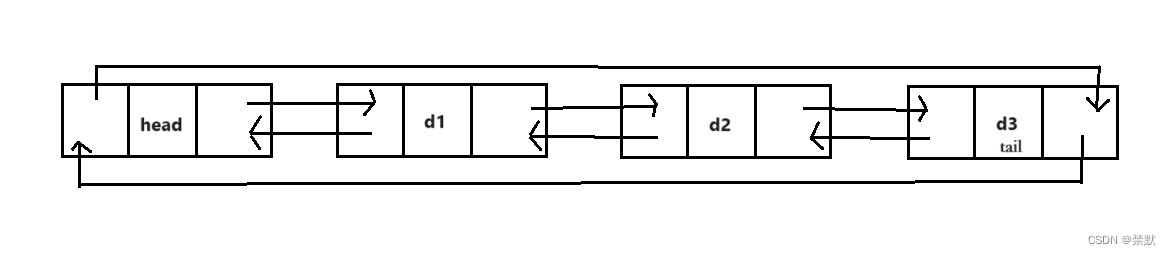
一.二叉树的顺序结构:
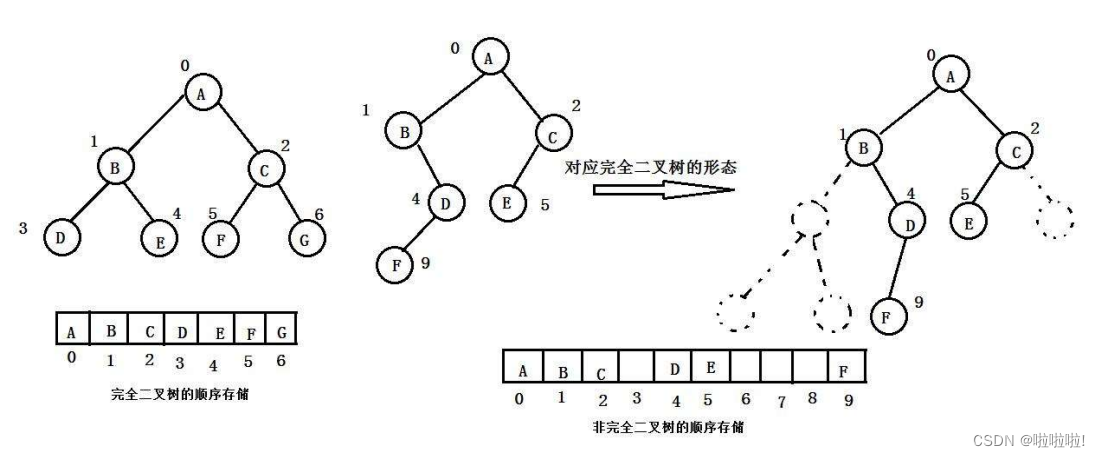
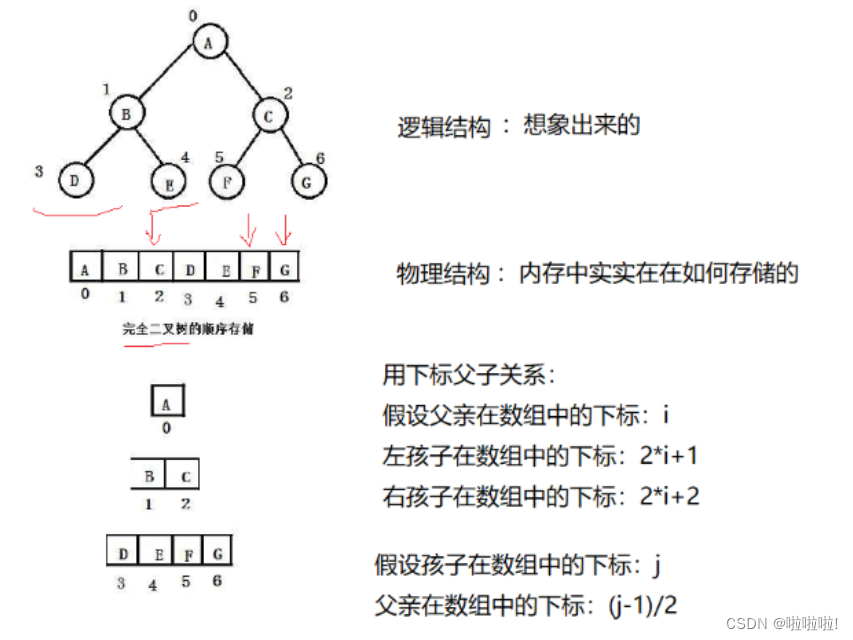
二.堆的概念及结构:
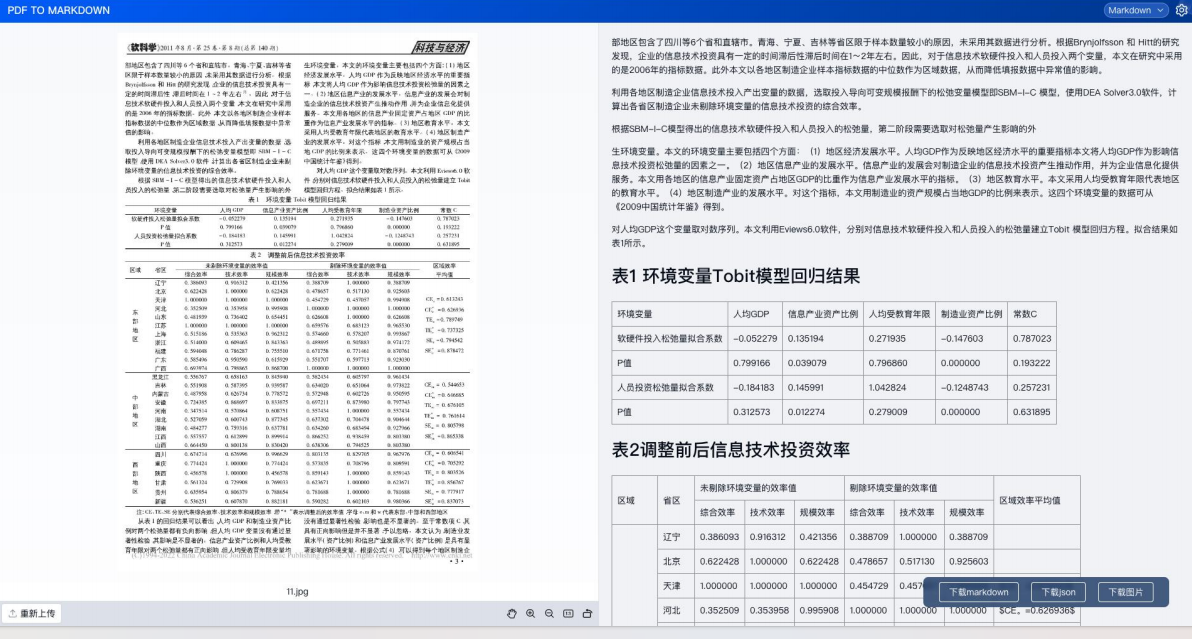
堆在物理结构上是数组,逻辑结构上就是完全二叉树。
1.大堆和小堆的介绍:
然而堆又分为大堆和小堆。大堆就是父亲节点大于等于孩子节点,小堆就是父亲节点小于等于孩子节点。
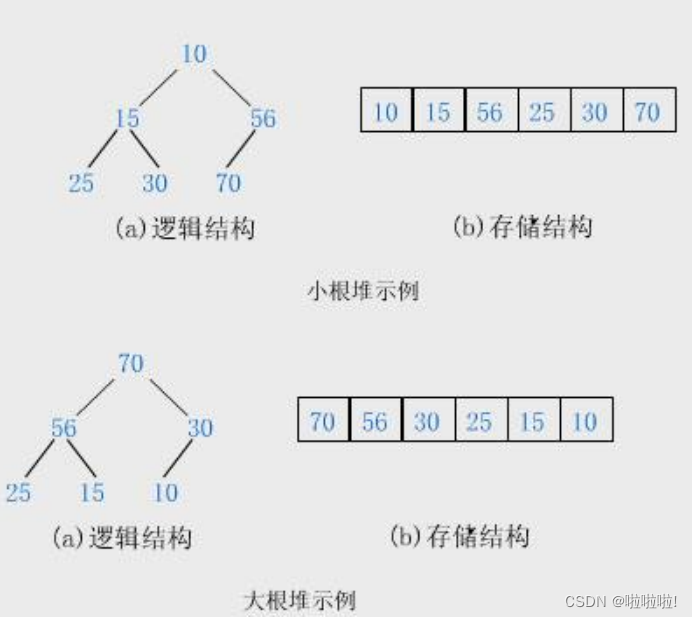
如图上面那个就是小堆,下面那个就是大堆。我们可以发现父亲和孩子是有关系的,但是兄弟之间是没有大小关系的。
三.堆的实现:
1.准备工作:
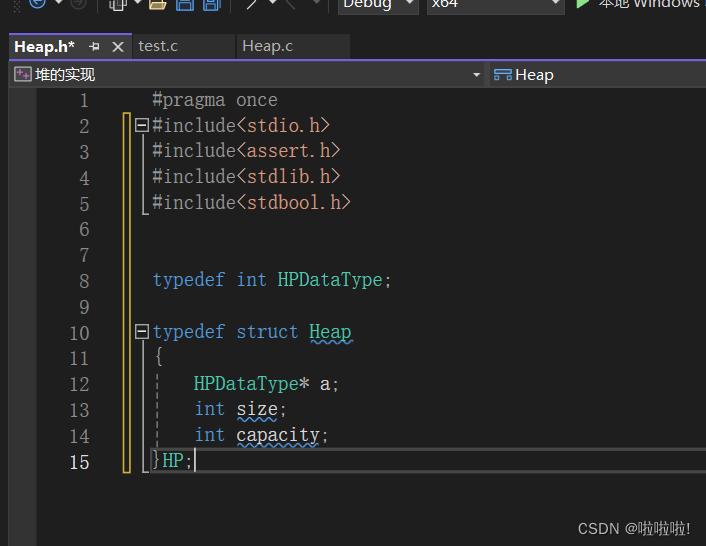
在物理结构上堆就是数组,所以这里有size来记录堆中数据的个数,capacity来记录堆的空间大小
2.堆的初始化:
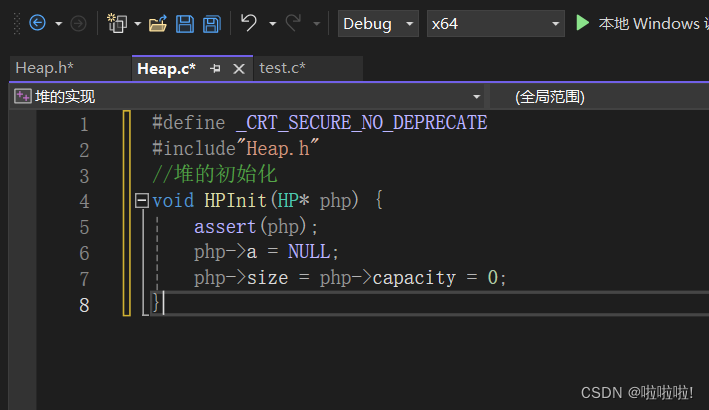
这里先不给数组开辟空间,当堆里插入数据时再开辟空间。
3.堆的销毁:
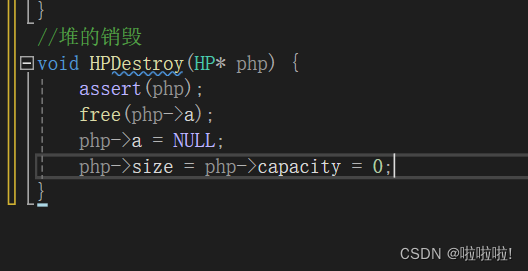
堆的销毁就是释放掉给堆存放数据的空间,然后令计数的变量为0即可。
在实现堆的插入时,实际上堆是一个完全二叉树,而堆又分为大堆和小堆,随便插入会导致堆的结构造成破坏,所以我们要提前写一个向上调整和向下调整的算法,来针对是大堆还是小堆的排序。
4.向上调整的算法:
实现向上算法之前,我们将要插入的那个数据的位置视为孩子,利用这个位置找到父亲节点。
上面写了孩子的下标为i,父亲的节点是(i-1)/2
拿这个图举列子,这个是建立小堆,所以小节点在上面。
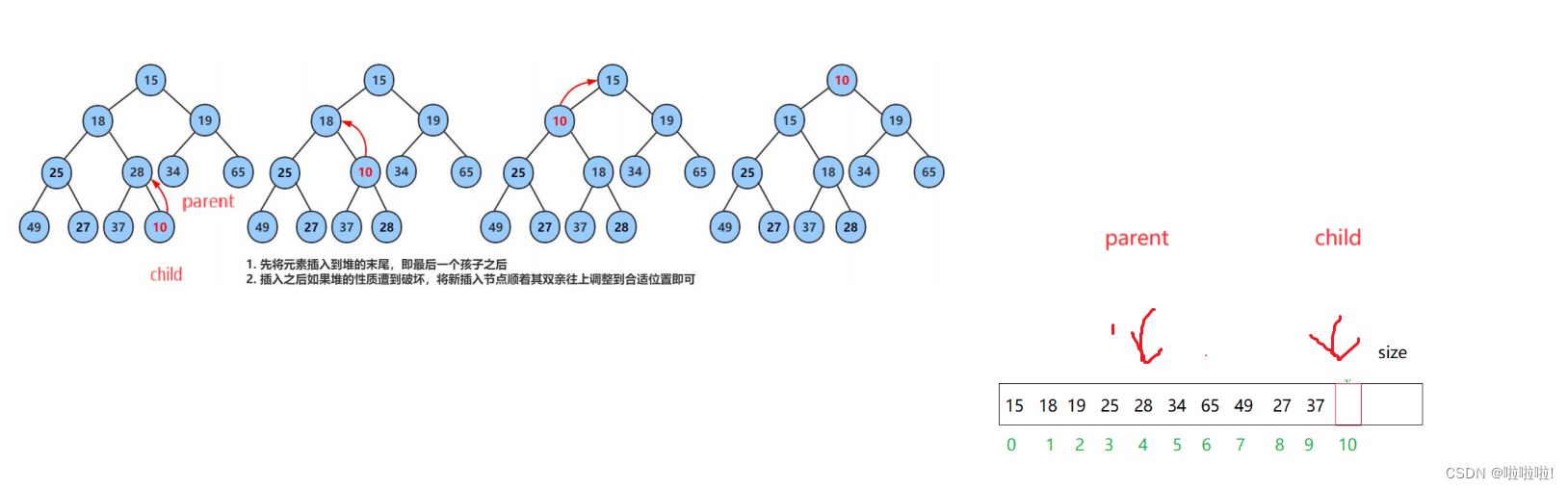
这里是按照小堆来调整的,所以当发现父亲比孩子大的数据就交换。
循环交替,互换父亲和孩子的位置,直到孩子的数组下标为0时循环就截至。
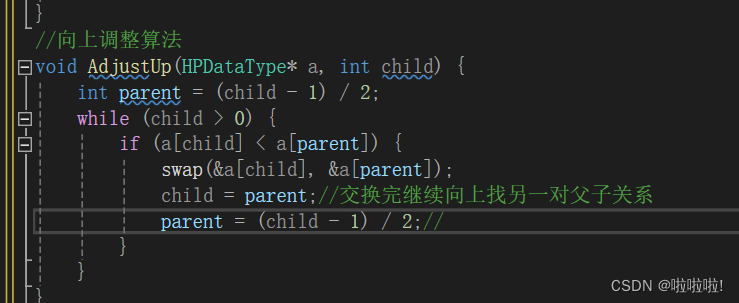
里面利用一个自己写的交换函数,然后交换完往上继续就行。
整个代码如图:
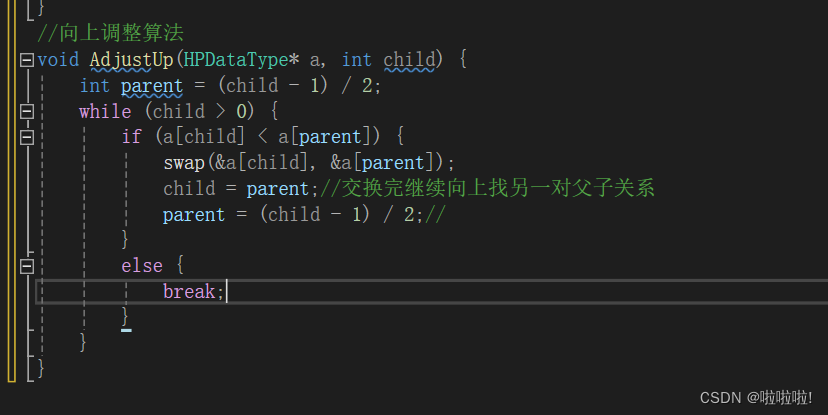
这里调整算法传参传的是一个数据类型的指针,而不是结构体指针,就是为了后面写堆排序有用。
现在我们写了向上调整的算法,我们就可以来实现建堆的插入数据的函数。
5.堆的插入:
先建立一个大堆或者小堆,然后插入数据(插入到最后一个叶子节点上),然后利用向上调整算法,使其大堆小堆的性质不发生改变。
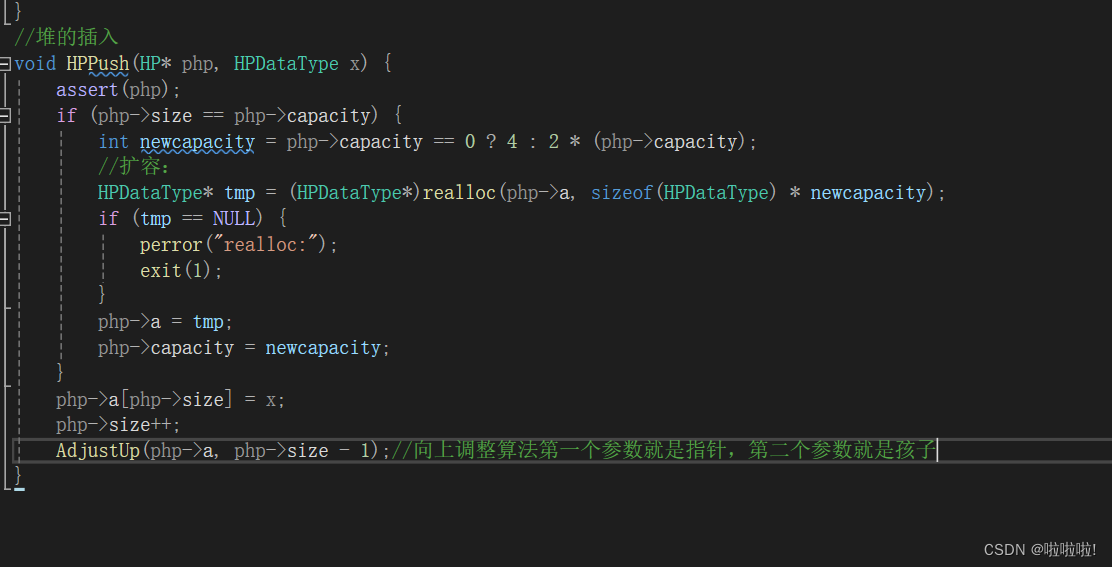
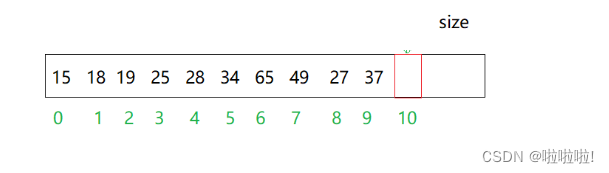
还是这个图,当数据成功插入到堆中后,此时调用向上调整算法,需要调整的孩子节点就是刚刚插入的那个数据,就是size-1的位置的数据。
此时我们来调试一下
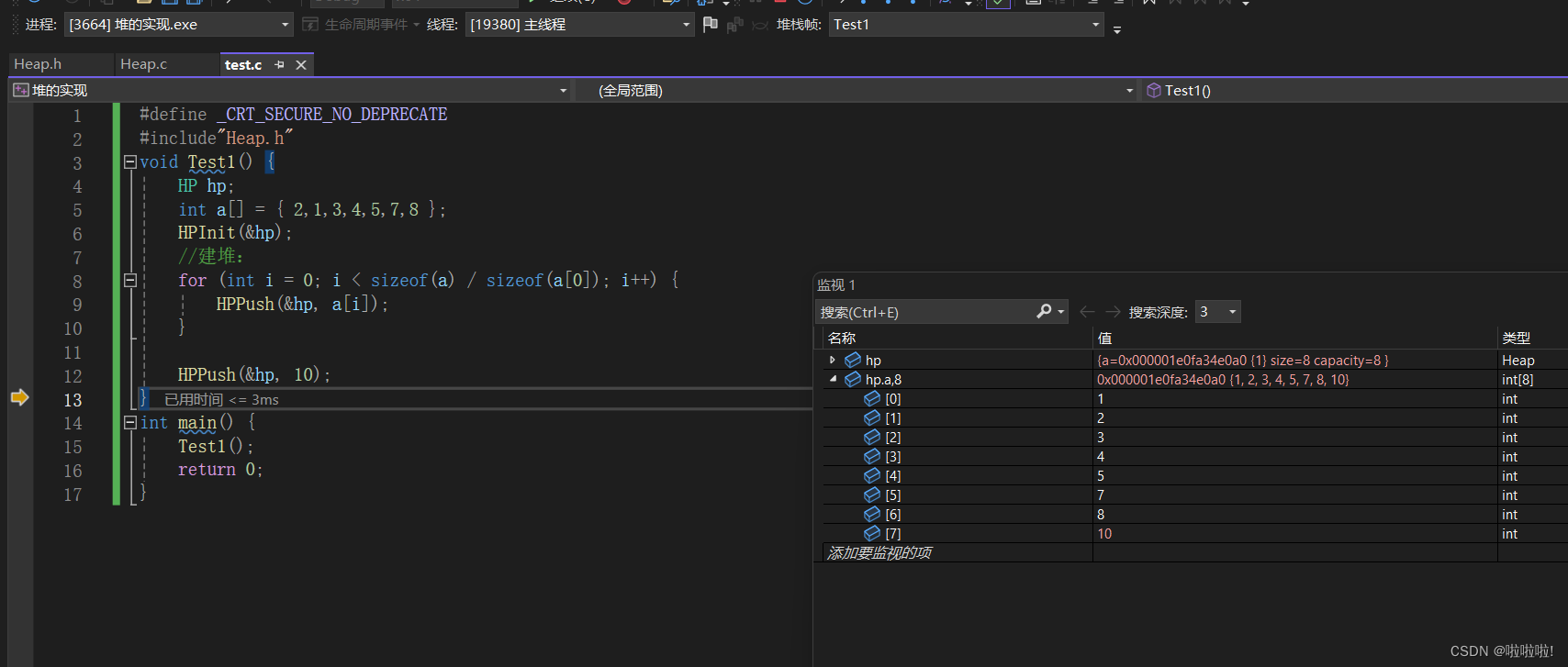
看看这些数据是否是小堆:

小堆就是父亲节点小于等于孩子节点。这个是完全没有问题的父亲节点都小于孩子节点。
所以这个函数的构造是没有问题的。
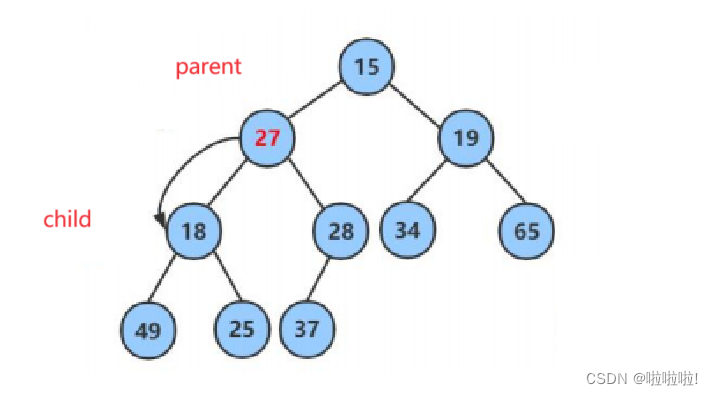
6.向下调整的算法:
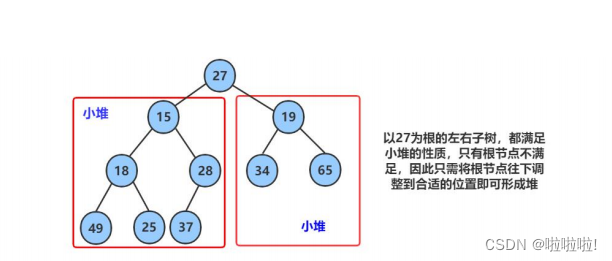

这里看出向下调整的过程:
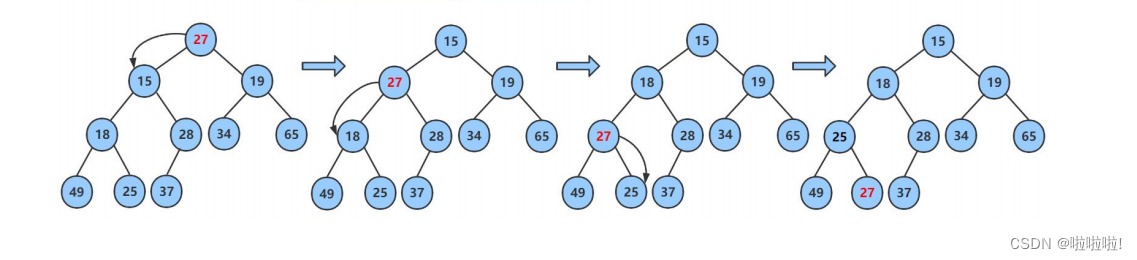
首先将那个要插入的数据作为头节点,让其作为父亲节点,向下找孩子节点,然后交换:
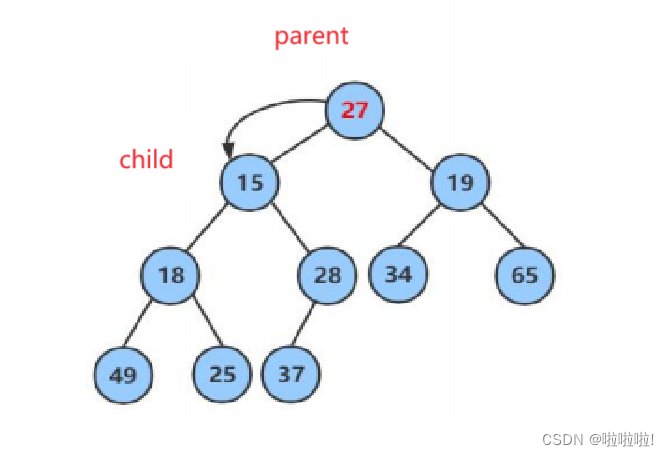
然后再将孩子节点传给父亲节点,然后继续往下找,直到孩子节点到达了叶子节点时循环就结束。
现在来编写代码:
这里的参数n就是代表从堆的哪个节点开始向下调整。
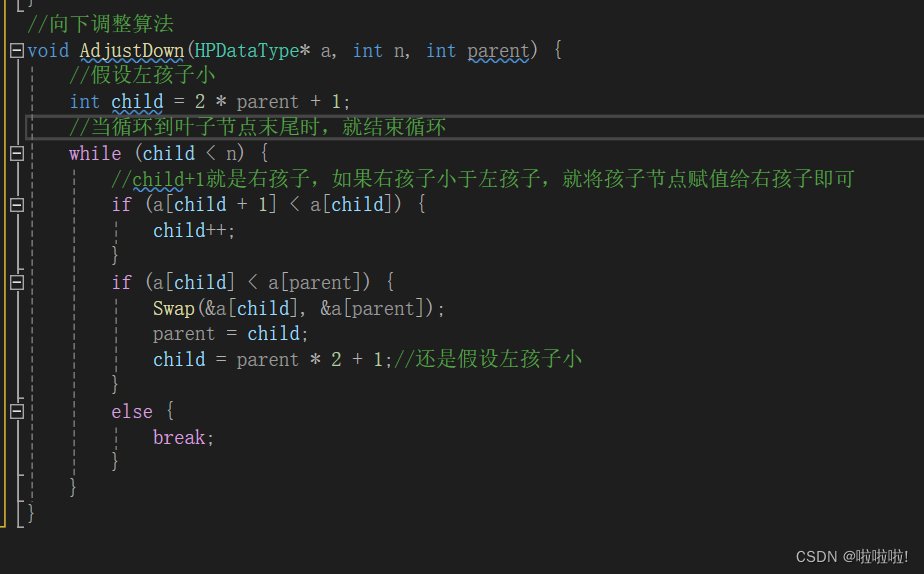
这里有可能会出现越界访问:
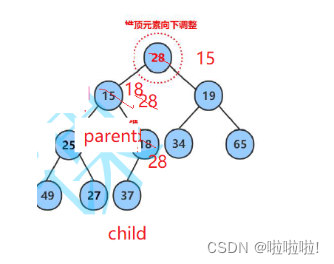
当走到后面的父亲节点时,如果是完全二叉树,有可能有没有右孩子的情况,所以这里要加一个限制条件以免越界访问。
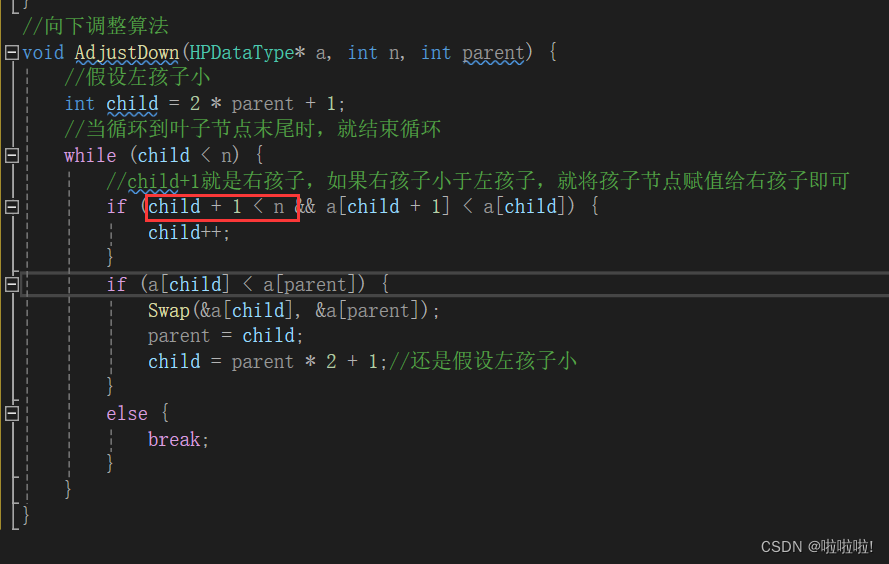
这样加了一个限制条件后就不会导致越界访问。
这里的实际意义就是,比如删除堆顶的数据时,此时是小堆,删除堆顶的数据后,再利用向下调整算法,这样就可以把堆里次小的数据找出来了,这样就可以用来排序。
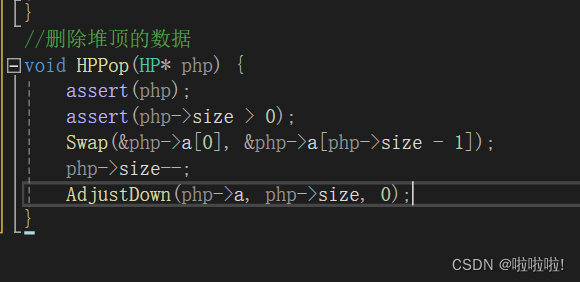
7.堆顶数据的删除:

此时想删除堆顶数据,如果直接将1覆盖会导致怎样的后果呢?

在这里关系就全乱了,原本是兄弟现在变成父子了,所以这里就不是小堆了,所以不能用挪动数据来覆盖。
在这里逻辑结构上的思路就是,你想防止下面的小堆不被打乱,所以这里我们只动堆顶和最后一个数据,我们将这两个数据交换一下:

此时在物理结构上的逻辑就是数组第一个和最后一个交换了一下,然后我们删除数组尾部的数据就特别好删除了。
物理结构上:

直接将记录数组大小的变量减减即可。所以这种办法不会导致关系变得混乱,也能很好的删除堆顶的数据。
交换完数据之后堆顶下边的两个子树还是满足小堆或者大堆,此时就可以使用向下调整算法,让交换完数据的堆还是保持原来的性质。
整个代码如图:
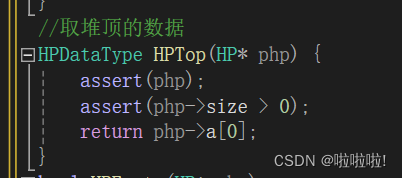
8.取堆顶的数据:
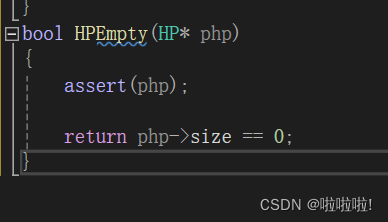
9.堆的判空:
总结:以上博客就是堆的整个实现的过程。