详解布隆过滤器（含面试考点）

Bloom Filter

底层逻辑
主要代码实现解析（以C++为例）
优缺点
应用场景
面试常问
- 问题1：什么是布隆过滤器？
- 问题2：布隆过滤器如何处理误报？
- 问题3：如何设计布隆过滤器以最小化误报率？
- 问题4：布隆过滤器有哪些应用场景？
- 问题5：布隆过滤器与哈希表有什么区别？
- 问题6：布隆过滤器在插入元素后，其准确性主要体现在哪些方面？
- 问题7：布隆过滤器的原理是什么？
- 问题8：布隆过滤器如何处理哈希碰撞？
- 问题9：在什么情况下不适合使用布隆过滤器？

底层逻辑

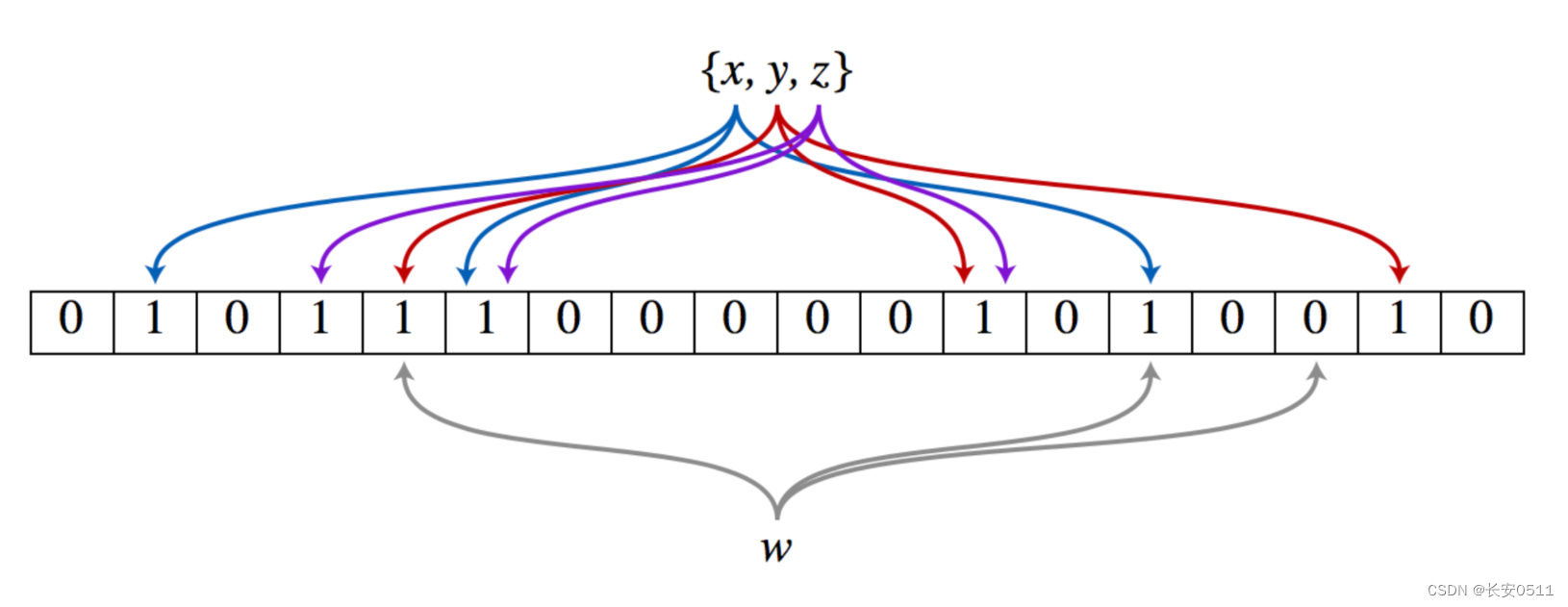
在这里插入图片描述

位数组：布隆过滤器使用一个很长的二进制位数组（bit array）来存储数据。这个数组的每个位置（bit）初始时都被设置为0。

哈希函数：布隆过滤器使用多个哈希函数（通常是k个不同的哈希函数）。每个哈希函数都能将输入的元素映射到位数组的某个位置上。具体来说，每个哈希函数会对元素进行哈希运算，并产生一个哈希值。这个哈希值会被模（取余）运算后，得到一个在位数组范围内的索引，该索引就是元素在位数组中的位置。

插入元素：当需要插入一个元素时，会用这个元素去计算k个哈希值，得到k个索引。然后，将位数组中这k个索引位置上的值都设置为1。

查询元素：当需要查询一个元素是否存在于集合中时，同样会用这个元素去计算k个哈希值，得到k个索引。然后，检查位数组中这k个索引位置上的值是否都为1。如果都为1，则认为该元素可能存在于集合中（注意是“可能”，因为存在哈希冲突的可能性）；如果至少有一个为0，则确定该元素不存在于集合中。

主要代码实现解析（以C++为例）

这里提供一个简化的布隆过滤器实现示例：

#include <iostream>
#include <bitset>
#include <functional> // for std::hash

class BloomFilter {
private:
    std::bitset<1000000> bitArray; // 位数组，假设大小为1000000
    std::hash<std::string> hashFunction; // 哈希函数对象

public:
    // 插入字符串元素到布隆过滤器中
    void insert(const std::string& str) {
        // 计算三次哈希值
        size_t hash1 = hashFunction(str);
        size_t hash2 = hashFunction(str + "salt"); // 添加盐增加哈希种子的多样性
        size_t hash3 = hashFunction(str + "pepper");

        // 将对应位数组位置设置为1
        bitArray[hash1 % bitArray.size()] = 1;
        bitArray[hash2 % bitArray.size()] = 1;
        bitArray[hash3 % bitArray.size()] = 1;
    }

    // 检查布隆过滤器中是否包含字符串元素
    bool contains(const std::string& str) {
        // 计算三次哈希值
        size_t hash1 = hashFunction(str);
        size_t hash2 = hashFunction(str + "salt");
        size_t hash3 = hashFunction(str + "pepper");

        // 检查对应位数组位置是否都为1
        return bitArray[hash1 % bitArray.size()] &&
               bitArray[hash2 % bitArray.size()] &&
               bitArray[hash3 % bitArray.size()];
    }
};

int main() {
    BloomFilter filter;

    // 插入一些示例字符串
    filter.insert("apple");
    filter.insert("banana");
    filter.insert("cherry");

    // 检查某些字符串是否存在于布隆过滤器中
    std::cout << "Contains apple: " << filter.contains("apple") << std::endl; // 应该返回1 (true)
    std::cout << "Contains grape: " << filter.contains("grape") << std::endl; // 应该返回0 (false)

    return 0;
}

优缺点

优点：

空间效率高：相比其他数据结构（如哈希表），布隆过滤器使用位数组来存储数据，因此空间占用非常小。
查询速度快：布隆过滤器的查询操作只涉及到位运算和哈希计算，因此查询速度非常快，接近O(1)时间复杂度。
灵活性高：布隆过滤器可以动态地添加元素，而不需要像传统数据结构那样进行扩容或重新哈希。

缺点：

误报率：布隆过滤器存在误报的可能性。当查询一个不存在的元素时，由于哈希冲突的存在，布隆过滤器可能会错误地认为该元素存在于集合中。误报率可以通过调整位数组大小和哈希函数数量来控制，但无法完全消除。
不支持删除操作：布隆过滤器不支持从集合中删除元素。一旦一个元素被插入到布隆过滤器中，就无法直接删除它。这是因为删除操作可能会影响到其他元素的判断结果。
哈希函数的选择：哈希函数的选择对布隆过滤器的性能有很大影响。如果哈希函数设计不好，可能会导致误报率过高。因此，在选择哈希函数时需要考虑其均匀性和独立性等特性。

应用场景

布隆过滤器在许多场景下都有广泛的应用，包括但不限于：

缓存穿透：在缓存系统中，布隆过滤器可以用来判断请求的数据是否存在于缓存中，从而避免直接穿透到数据库层。
垃圾邮件过滤：布隆过滤器可以用来过滤已知的垃圾邮件地址或内容，减少不必要的邮件处理开销。
Web爬虫：在Web爬虫中，布隆过滤器可以用来记录已经爬取过的URL，避免重复爬取。
推荐系统：在推荐系统中，布隆过滤器可以用来快速判断用户是否对某个物品感兴趣（基于历史行为数据），从而快速生成推荐列表。

面试常问

问题1：什么是布隆过滤器？

解答：布隆过滤器是一个空间效率极高的概率型数据结构，它利用位数组和哈希函数来判断一个元素是否可能存在于一个集合中。布隆过滤器可以快速地告诉你某个元素很可能不存在于集合中（没有误报），或者某个元素可能存在（有误报）。

问题2：布隆过滤器如何处理误报？

解答：布隆过滤器存在误报的可能性，即它可能会错误地认为某个元素存在于集合中。这是由于哈希冲突和位数组的空间限制导致的。然而，布隆过滤器不会漏报，即它永远不会错误地告诉你某个元素不存在于集合中。如果布隆过滤器返回可能存在，那么你需要使用其他方法（如数据库查询）来确认该元素是否真的存在。

问题3：如何设计布隆过滤器以最小化误报率？

解答：要最小化布隆过滤器的误报率，你可以考虑以下方法：

增加位数组的大小：位数组越大，误报率越低。但是，这也会增加布隆过滤器的存储空间和计算成本。
增加哈希函数的数量：使用更多的哈希函数可以进一步降低误报率。但是，这也会增加计算复杂性和时间成本。
选择合适的哈希函数：哈希函数的选择对布隆过滤器的性能有很大影响。你应该选择那些均匀分布且独立的哈希函数。

问题4：布隆过滤器有哪些应用场景？

解答：布隆过滤器在许多场景下都有广泛的应用，包括但不限于：

缓存穿透：在缓存系统中，布隆过滤器可以用来判断请求的数据是否存在于缓存中，从而避免直接穿透到数据库层。
垃圾邮件过滤：布隆过滤器可以用来过滤已知的垃圾邮件地址或内容，减少不必要的邮件处理开销。
Web爬虫：在Web爬虫中，布隆过滤器可以用来记录已经爬取过的URL，避免重复爬取。
推荐系统：在推荐系统中，布隆过滤器可以用来快速判断用户是否对某个物品感兴趣（基于历史行为数据），从而快速生成推荐列表。

问题5：布隆过滤器与哈希表有什么区别？

解答：布隆过滤器和哈希表在数据结构上有很大的区别。哈希表是一种确定性的数据结构，它使用哈希函数将键映射到桶中，并存储相应的值。哈希表可以准确地告诉你一个键是否存在（没有误报和漏报）。然而，哈希表需要为每个键存储值，因此其空间效率相对较低。布隆过滤器则是一种概率型数据结构，它只使用位数组和哈希函数来判断元素是否存在。布隆过滤器可以快速地告诉你一个元素很可能不存在（没有误报），但可能会误报。由于布隆过滤器不需要存储值，因此其空间效率非常高。

问题6：布隆过滤器在插入元素后，其准确性主要体现在哪些方面？

正确拒绝（False Negative）：如果一个元素从未被添加到布隆过滤器中，并且布隆过滤器正确地判断它不存在，那么这是一个正确的结果（没有误报）。布隆过滤器永远不会错误地报告一个从未被添加的元素存在，即它不会产生假阴性（False Negative）。
误报（False Positive）：然而，布隆过滤器的一个主要限制是可能会产生误报（False Positive）。这意味着布隆过滤器可能会错误地报告一个实际上并未被添加的元素存在。这是由于哈希冲突和位数组的空间限制导致的。当两个或多个不同的元素在多个哈希函数的作用下映射到位数组的相同位置时，这些位置上的位都会被设置为1。因此，当查询一个从未被添加的元素时，如果这些位置上的位都是1，布隆过滤器就会错误地认为该元素存在。

布隆过滤器的误报率取决于几个因素，包括位数组的大小、哈希函数的数量以及添加到过滤器中的元素数量。位数组越大，哈希函数数量越多，误报率就越低。但是，这也会增加布隆过滤器的存储空间和计算成本。因此，在设计布隆过滤器时，需要根据具体的应用场景和需求来权衡这些因素。

需要注意的是，虽然布隆过滤器可能会产生误报，但它通常用于那些可以容忍一定误报率的场景。例如，在缓存穿透、垃圾邮件过滤和Web爬虫等应用中，即使布隆过滤器偶尔会产生误报，也不会对整体应用产生太大的影响。在这些场景中，布隆过滤器的优点（如空间效率高、查询速度快）往往超过了其可能产生的误报率所带来的缺点。

问题7：布隆过滤器的原理是什么？

解答：布隆过滤器基于位数组和哈希函数。当一个元素被加入到布隆过滤器中时，通过多个哈希函数对该元素进行哈希计算，得到多个哈希值，然后将对应的位数组位置设为1。当需要判断一个元素是否存在于布隆过滤器中时，同样通过多个哈希函数计算该元素的哈希值，并检查对应的位数组位置是否都为1。如果所有位置都为1，则说明该元素可能存在于集合中；如果存在任意一个位置不为1，则说明该元素一定不在集合中。