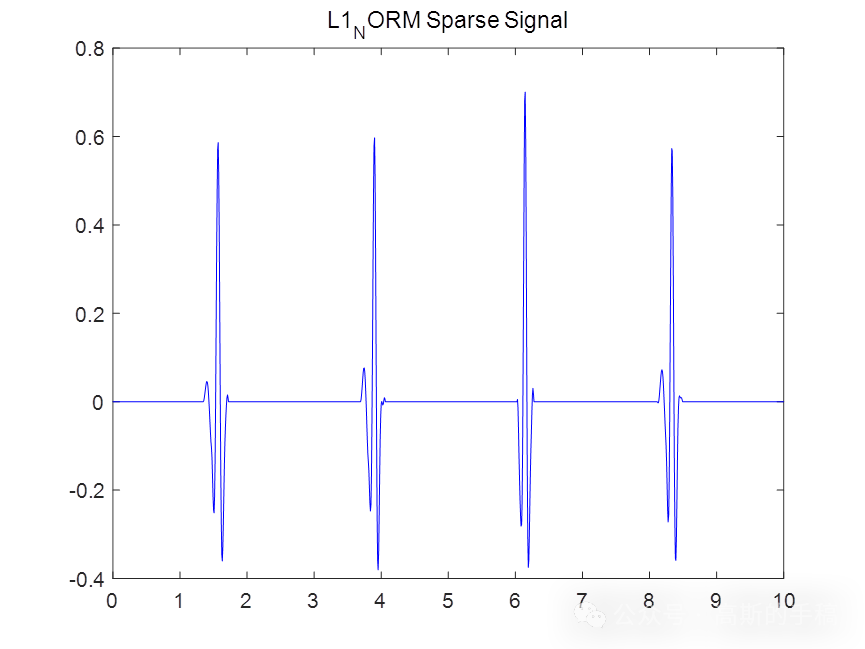
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一定范围内是发散的,而L1范数正则化方法的解通常是稀疏的。
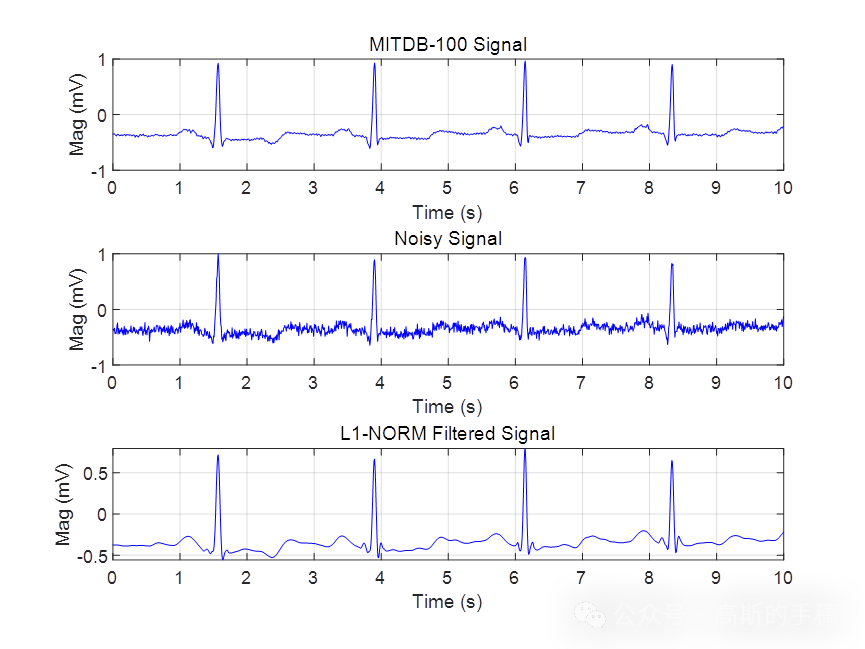
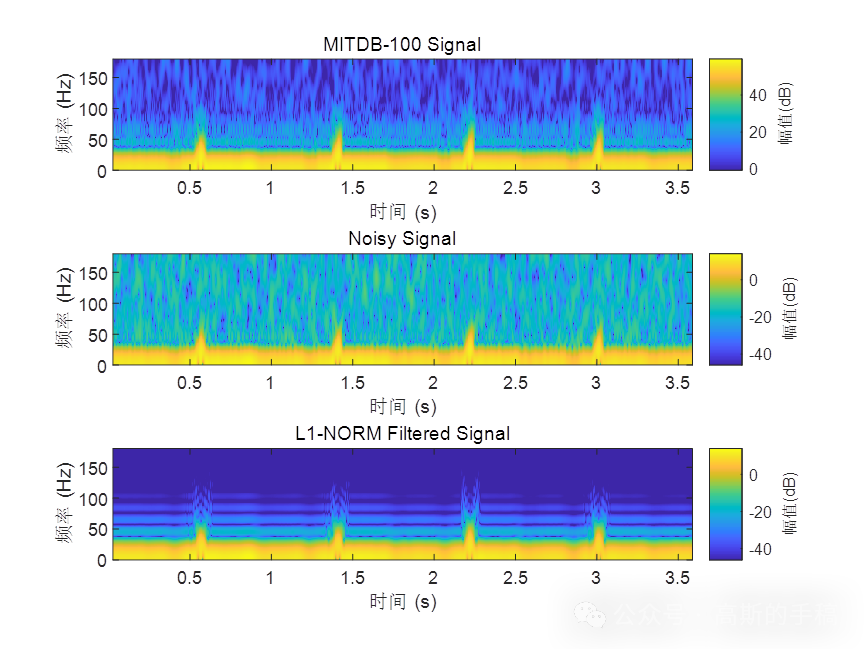
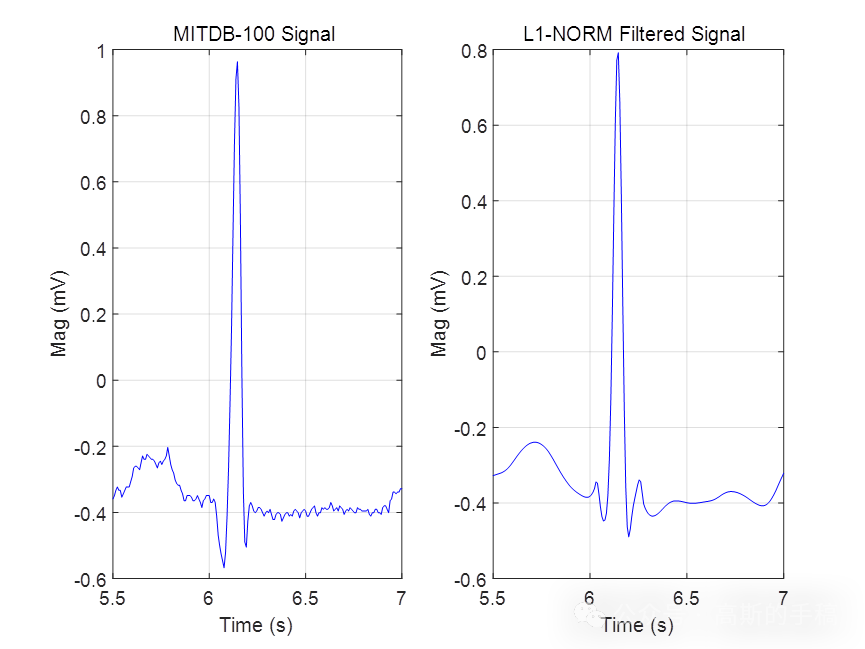
鉴于此,采用L1范数惩罚的稀疏正则化最小二乘方法对心电信号进行降噪,算法可迁移至金融时间序列,地震信号,语音信号,声信号,生理信号等一维时间序列信号,运行环境为MATLAB R2021B,主算法代码如下:
function [x, cost, delta_x] = L1NORM(y, A, AH, rho, lam)
% x = srls_L1(y, A, AH, rho, lam)
%
% Minimize ||y - A x||_2^2 + lam ||x||_1
%
% INPUT
% y : data
% A, AH : function handles for A and its conj transpose
% rho : rho >= maximum eigenvalue of A'A
% lam : regularization parameter, lam > 0
%
% OUTPUT
% x : solution
%
% [x, cost] = srls_L1(...) returns cost function history
% Algorithm: ISTA (forward-backward splitting)
MAX_ITER = 10000;
TOL_STOP = 1e-4;
% soft thresholding for complex data
soft = @(x, T) max(1 - T./abs(x), 0) .* x;
cost = zeros(1, MAX_ITER); % cost function history
mu = 1.9 / rho;
% Initialization
AHy = AH(y); % A'*y
x = AH(zeros(size(y)));
Ax = A(x);
iter = 0;
old_x = x;
delta_x = [inf];
while (delta_x(end) > TOL_STOP) && (iter < MAX_ITER)
iter = iter + 1;
z = x - mu * ( AH(Ax) - AHy );
x = soft(z, lam * mu);
Ax = A(x);
% cost function history
residual = y - Ax;
cost(iter) = 0.5 * sum(abs(residual(:)).^2) + lam * sum(abs(x(:))) ;
delta_x(iter) = max(abs( x(:) - old_x(:) )) / max(abs(old_x(:)));
old_x = x;
end
%完整代码:https://mbd.pub/o/bread/mbd-ZZaZmplr
cost = cost(1:iter);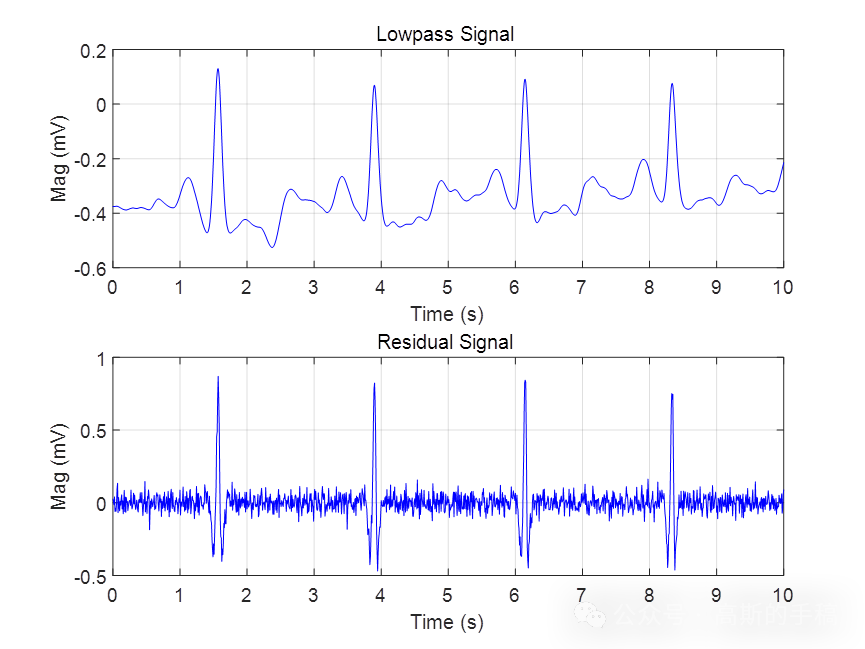
完整代码:https://mbd.pub/o/bread/mbd-ZZaZmplr
工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。