文章目录
- 0. 概述
- 1. 无前缀冲突编码
- 2. 编码成本
- 3. 带权编码成本
- 4. 编码算法
- 5. 算法实现流程
- 6. 时间复杂度与改进方案
0. 概述
学习Huffman树。
1. 无前缀冲突编码
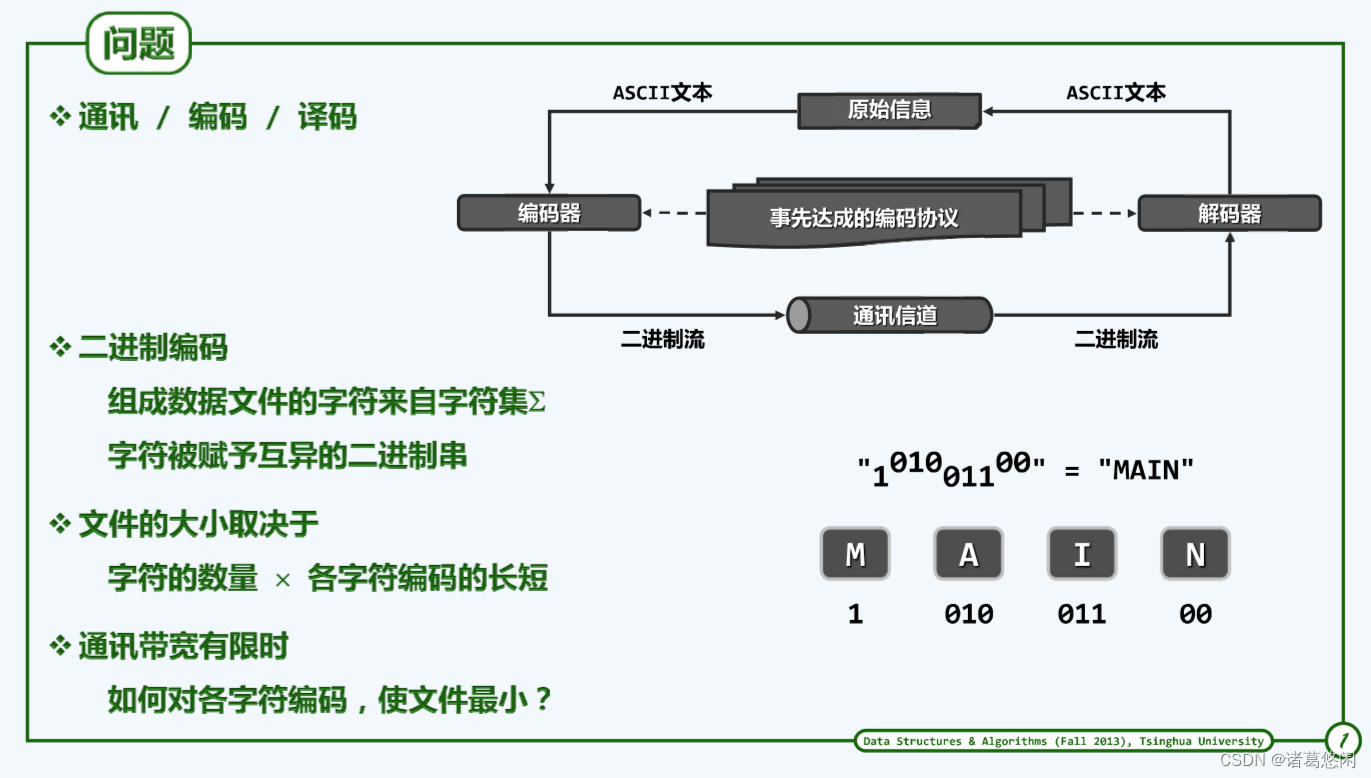
在加载到信道上之前,信息被转换为二进制形式的过程称作编码(encoding);反之,经信道抵达目标后再由二进制编码恢复原始信息的过程称作解码(decoding)。
编码和解码的任务分别由发送方和接收方分别独立完成,故在开始通讯之前,双方应已经以某种形式,就编码规则达成过共同的约定或协议。
解码策略——前缀无歧义编码PFC(prefix-free code):按顺序对信息比特流做子串匹配的策略,因此为消除匹配的歧义性,任何两个原始字符所对应的二进制编码串,相互都不得是前缀。
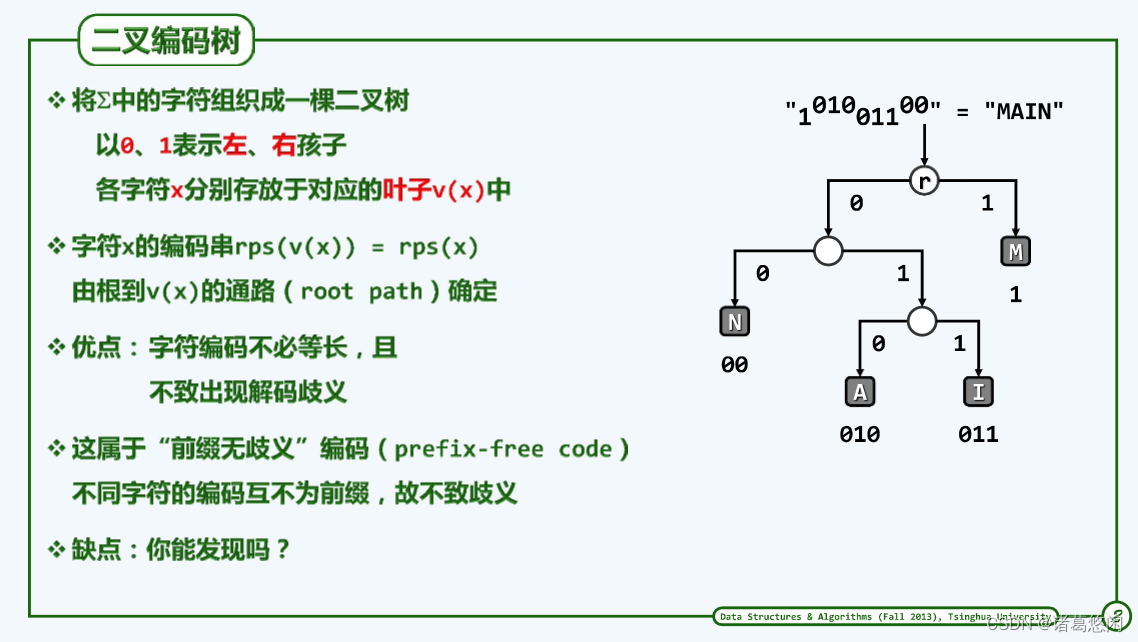
利用二叉编码树方法可解决消息解码歧义问题,可以使通讯双方交换信息,进行沟通。
2. 编码成本
接下来讨论新的问题——如何使编码更有效? 首先来看如何对编码长度做“度量”。
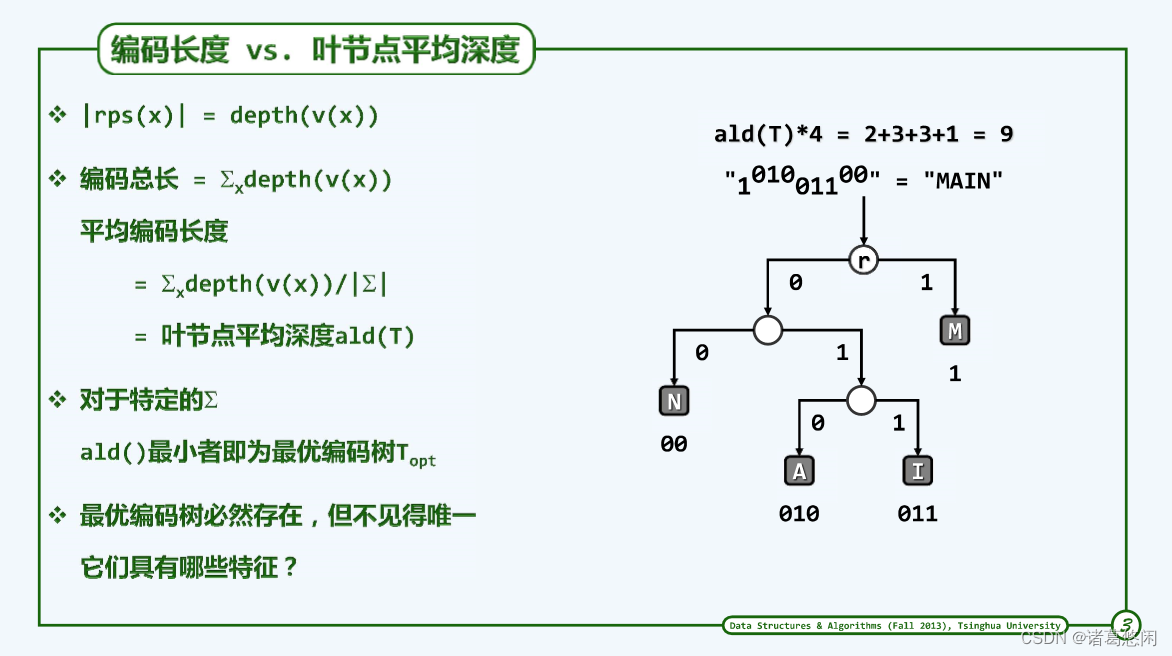
字符x的编码长度|rps(x)|就是其对应叶节点的深度depth(v(x))。
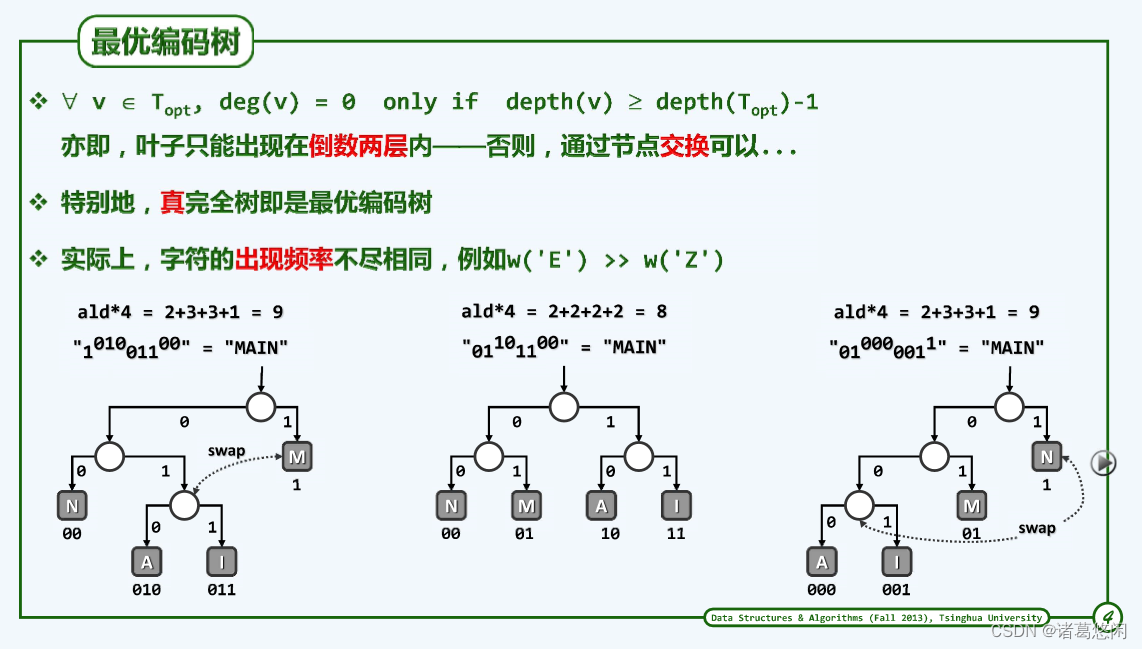
上图都是对四个字符MAIN同一编码表的三种编码方式——左中右。它们的编码长度是不一样的,发送MAIN单词,左边占9bit,中间占8bit,右边占9bit,中间的编码长度相对较优,需要这么较劲吗?会影响到带宽、费用、成本和用户体验。
问题关键点——怎么才能编程最优编码方式呢?
通过观察不难得出,树结构越平衡越好——杜绝树中节点深度差过大(大于等于2)。再接着问,如何让树变的平衡呢?
结论:
- 最优二叉编码树必为真二叉树:内部节点的左、右孩子全双。
- 最优编码树中,叶节点位置的选取有严格限制——其深度之差不得超过1。
叶子只能出现在倒数两层内——否则,通过节点交换可以。
3. 带权编码成本
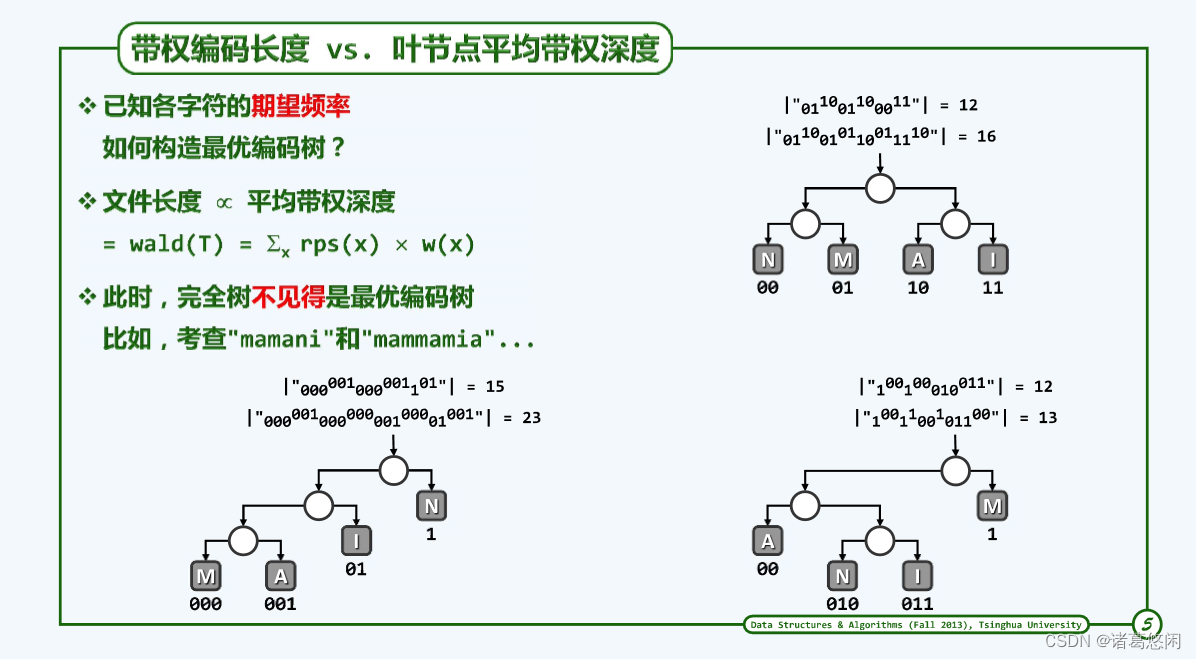
以上最优编码树算法的实际应用价值并不大,除非中各字符在文本串中出现的次数相等。因此需面对一个事实——词频差异很大,这种情况下,完全树未必就是最优编码树,如上图,应该从另一角度更为准确地衡量平均编码长度。
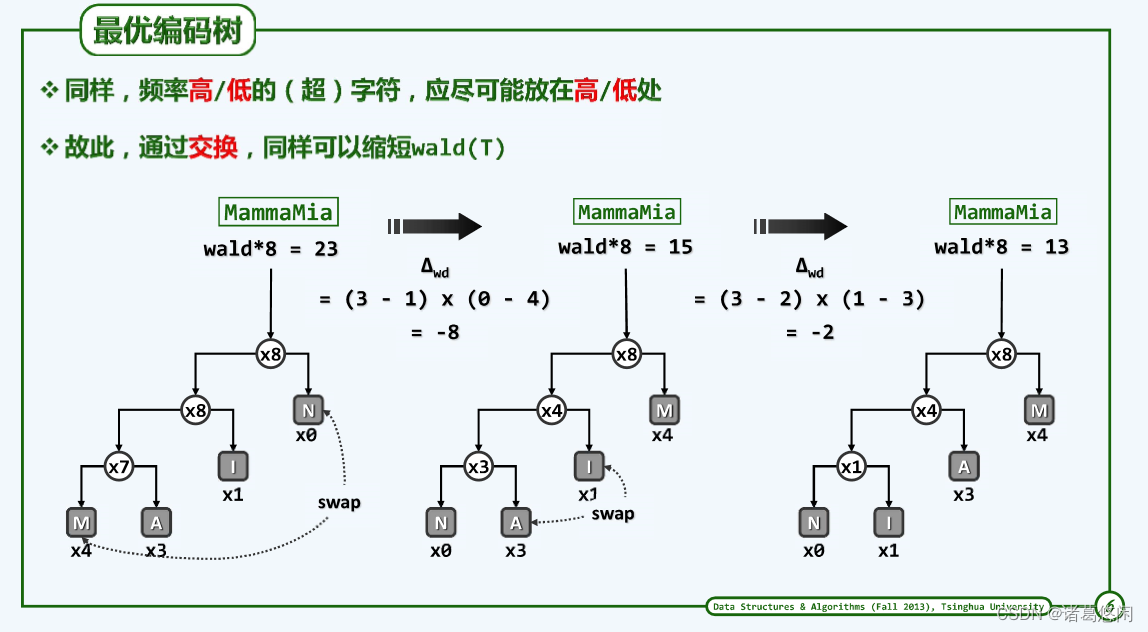
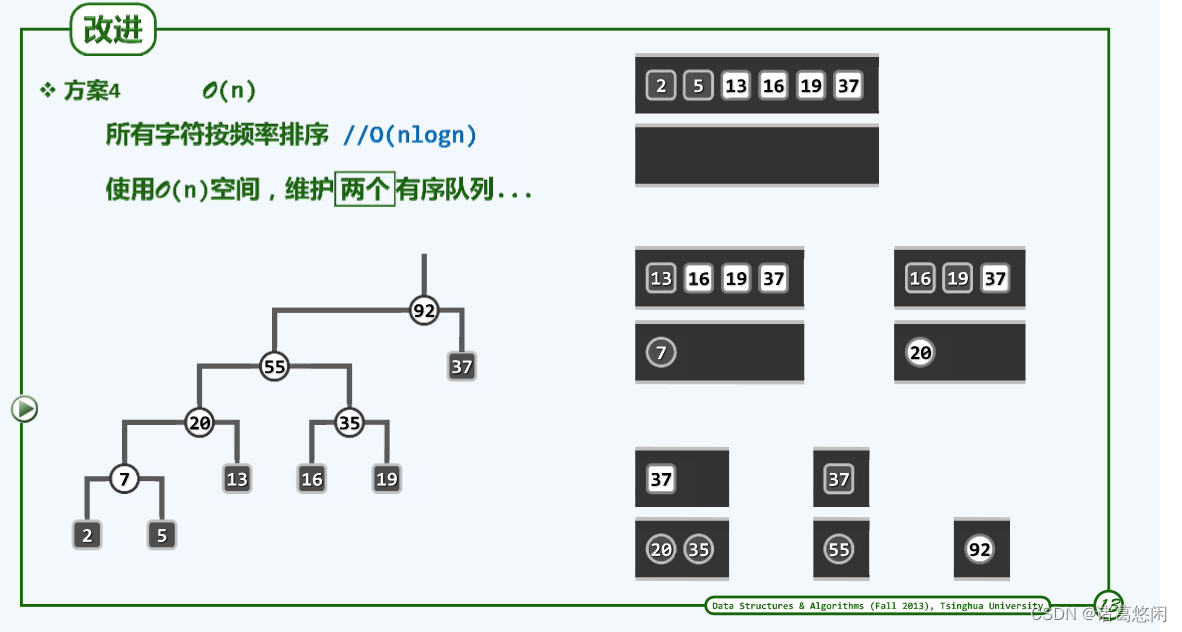
总结:让频率更高的字符放在树高处,让频率更低的字符放在树的低处。
4. 编码算法

结论:尽管贪心策略未必总能得到最优解,但非常幸运,如上算法的确能够得到最优编码树之一。
5. 算法实现流程
- 总体框架

- 最小超字符

- 构造编码表

6. 时间复杂度与改进方案