人工智能-作业3

计科210X 甘晴void 202108010XXX
1.贝叶斯网络
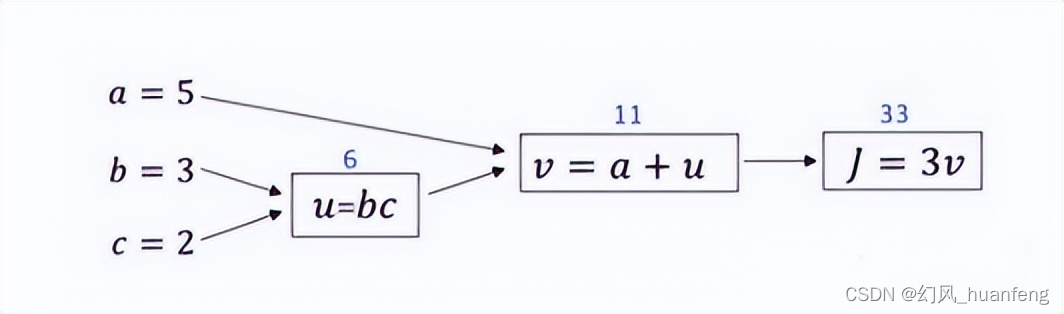
根据图所给出的贝叶斯网络,其中:P(A)=0.5,P(B|A)=1, P(B|¬A)=0.5, P(C|A)=1, P(C|¬A)=0.5,P(D|BC)=1,P(D|B, ¬C)=0.5,P(D|¬B,C)=0.5,P(D|¬B, ¬C)=0。试计算下列概率P(A|D)。

解:

2.不确定性的量化
某学校,所有的男生都穿裤子,而女生当中,一半穿裤子,一半穿裙子。男女比例70%的可能性是4:6,有20%可能性是1:1,有10%可能性是6:4,问一个穿裤子的人是男生的概率有多大?
解:

3.决策树
设样本集合如下表格,其中A、B、C是F的属性,请根据信息增益标准(ID3算法),画出F的决策树。其中

| A | B | C | F |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
解:

4.人工神经网络
阈值感知器可以用来执行很多逻辑函数,说明它对二进制逻辑函数与(AND)和或(OR)的实现过程。
解:
二进制逻辑函数与(AND)和或(OR)只在训练样本上有区别,在训练过程上是一致的。
这是与(AND)函数的训练样本
| X1 | X2 | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
这是或(OR)函数的训练样本
| X1 | X2 | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
下面我们以AND为例,进行一次训练过程
这是感知机示意图
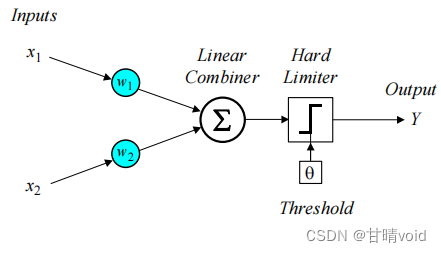
下面是训练步骤:
-
(1)初始化:设定初始的权值w1,w2,和θ阈值为[-0.5,0.5]之间的随机数,(即刚开始的数值不重要,后续都会通过样本迭代修正收敛)
-
(2)计算得到Y(p):根据输入x1 (p), x2 (p) 和权值w1,w2计算输出Y(p),其中p表示迭代的轮数
-
(3)更新权值:按照下述公式计算下一轮的权重值
-
e(p) = Yd(p) - Y(p) -
Δwi(p) = α · xi(p) · e(p) -
wi(p+1) = wi(p) + Δwi(p)
-
-
(4)迭代循环:增加p值,不断重复步骤(2)-(3)直到收敛(即e在一段循环间小于一个较小值)
我使用python写了一个简单的逻辑
import numpy as np
# 简单感知器
class Perceptron(object):
def __init__(self, lr, epoch):
# 指定 X 维度数,这里是2
self.input_dim = 2
# 指定激活函数,这里用阶跃函数
self.activator = self.__step
# 指定学习率与训练轮数
self.lr = lr
self.epoch = epoch
# 权重向量初始化为[-0.5,0.5]随机数
self.weights = np.random.uniform(-0.5, 0.5, self.input_dim)
self.bias = np.random.uniform(-0.5, 0.5)
# 阶跃函数
def __step(self, x):
return 1 if x > 0 else 0
# 返回感知机的参数
def __str__(self):
return 'weight: %s\n bias: %f\n' % (self.weights, self.bias)
# 正向传播
def __forward(self, X):
y_temp = np.dot(self.weights, X) + self.bias
Y = self.activator(y_temp)
return Y
# 训练
def __train(self, inputs, labels):
for _ in range(self.epoch):
samples = zip(inputs, labels)
for input, label in samples:
output = self.__forward(input)
self.__update_weights(input, output, label)
# 反向传播,更新数值
def __update_weights(self, input, output, label):
delta = label - output
self.weights += self.lr * delta * input
self.bias += self.lr * delta
# 训练(外部接口)
def train(self, inputs, labels):
self.__train(inputs, labels)
# 预测(外部接口)
def predict(self, X):
return self.__forward(X)
def get_train_dataset(mode):
# 构建训练数据
if mode=="and":
input_vecs = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # X
labels = np.array([0, 0, 0, 1]) # labels
return input_vecs, labels
if mode=="or":
input_vecs = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # X
labels = np.array([0, 1, 1, 1]) # labels
return input_vecs, labels
if __name__ == "__main__":
# 选择模式 and 还是 or , 直接输入即可
mode = "or"
# 实例化感知机
perceptron = Perceptron(lr=0.001,epoch=1000)
# 获取数据集
input_vecs, labels = get_train_dataset(mode=mode)
# 训练
perceptron.train(input_vecs, labels)
# 输出权重信息
print(perceptron)
#测试真值表
print("0 {mode} 0 = {ans}".format(mode=mode,ans=perceptron.predict([0, 0])))
print("0 {mode} 1 = {ans}".format(mode=mode,ans=perceptron.predict([0, 1])))
print("1 {mode} 0 = {ans}".format(mode=mode,ans=perceptron.predict([1, 0])))
print("1 {mode} 1 = {ans}".format(mode=mode,ans=perceptron.predict([1, 1])))
可以运行看看结果
# or
weight: [0.10514797 0.49573695]
bias: -0.104832
0 or 0 = 0
0 or 1 = 1
1 or 0 = 1
1 or 1 = 1
# and
weight: [0.12922707 0.00225016]
bias: -0.131045
0 and 0 = 0
0 and 1 = 0
1 and 0 = 0
1 and 1 = 15.深度学习
深度学习的原理是什么?以一个典型的深度学习算法为例进行说明。
解:
【深度学习的原理】
深度学习的原理主要基于神经网络模型的训练和优化,它包含了多个层次的神经元,每一层都会对输入数据进行一系列非线性变换和特征提取,最终输出结果。
★深度学习相对于普通神经网络的主要特点在于:使用包含多个隐层的深层神经网络。这也是深度学习为什么能够做的比普通神经网络好的原理所在。
典型的深度学习算法包括卷积神经网络(Convolutional Neural Networks, CNN)、循环神经网络(Recurrent Neural Networks, RNN)、长短期记忆网络(Long Short-Term Memory, LSTM)和注意力机制(Attention Mechanism)等。
【举例说明】
接下来我将以典型深度学习模型之一的 Transformer 为例,简要说明深度学习(主要是注意力机制)的原理:
这是经典的《attention is all you need》论文中的transformer结构

(1)原理概述
Transformer 是一种用于处理序列数据的深度学习模型,最初用于自然语言处理任务,如机器翻译和语言建模。其核心思想是完全基于注意力机制,通过自注意力机制(self-attention mechanism)来捕捉输入序列中的依赖关系,从而实现对序列数据的建模和处理。
(2)自注意力机制(Self-Attention Mechanism)
自注意力机制是 Transformer 模型的核心组成部分,用于学习序列中不同位置之间的关系。在自注意力机制中,每个输入位置都可以与其他所有位置进行交互,从而使得模型能够在不同位置之间学习到不同程度的依赖关系。
自注意力机制的计算过程如下:
-
对于输入序列中的每个位置,计算其与所有其他位置的注意力权重。
-
使用注意力权重对所有位置的特征进行加权求和,得到每个位置的输出表示。
Attention(multi)包括三个注意力层
-
(encoder)自注意力层
-
(decoder)遮盖多头注意力层
-
(decoder)交互注意力层
(3)Transformer 模型结构
Transformer 模型由编码器(Encoder)和解码器(Decoder)组成,每个编码器和解码器都由多个注意力层和前馈神经网络层组成。
-
编码器(Encoder):用于将输入序列编码为表示丰富的特征向量,其中每个位置都包含输入序列的全局信息。
-
包含多个注意力层(self-attention)和前馈神经网络层。
-
-
解码器(Decoder):根据编码器生成的特征向量来生成输出序列。
-
包含多个注意力层(self-attention)和编码器-解码器注意力层(encoder-decoder attention)以及前馈神经网络层。
-
(4)Transformer 训练过程
-
输入序列经过编码器得到特征表示。
-
特征表示经过解码器生成输出序列。
-
训练过程中通过反向传播算法更新模型参数,使得模型输出的序列尽可能地接近目标序列。
(5)优势
-
可并行化处理:Transformer 模型中的注意力机制使得模型能够并行化处理输入序列中的不同位置,从而加速模型训练和推理过程。
-
长距离依赖建模:通过自注意力机制,Transformer 能够更好地捕捉输入序列中不同位置之间的长距离依赖关系,从而提高模型的建模能力。
参考答案
第1题

第2题

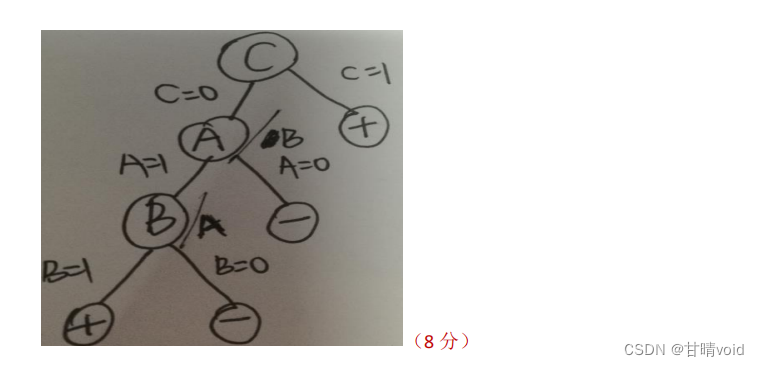
第3题


第4题

第5题
略