3. 格林应变与阿尔曼西应变

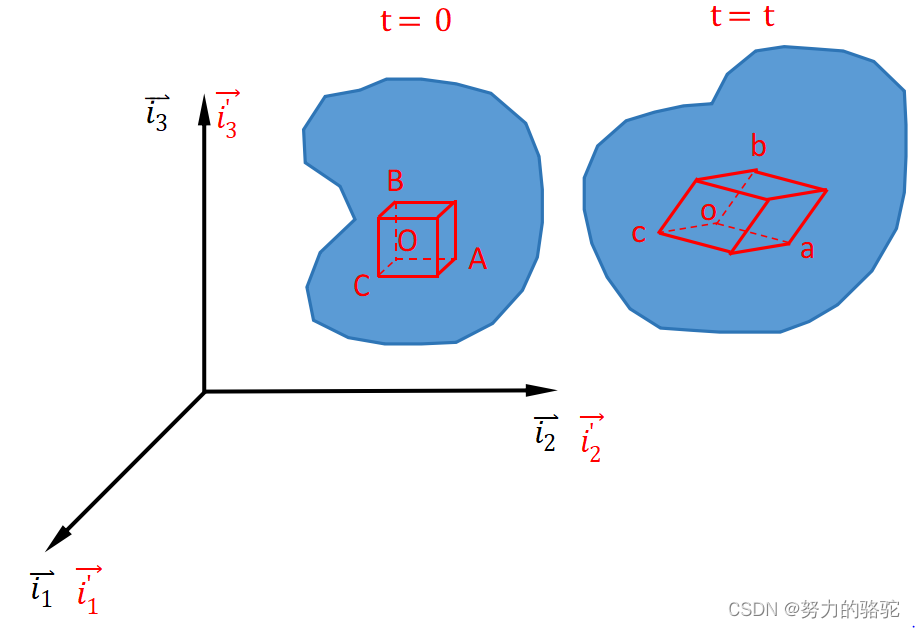
变形体在变形前的线元$\overrightarrow{OA}$，在变形后变成$\overrightarrow{oa}$，那么应变应该度量这种线元变形前后的差别。
$$\begin{array}{rl}|\overrightarrow{oa}{|}^2-|\overrightarrow{OA}{|}^2& =d{x}_{i}d{x}_i-d{x}_i^{{}^{\prime }}d{x}_i^{{}^{\prime }}\\ & =\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}d{x}_j^{{}^{\prime }}\cdot \frac{\partial x_i}{\partial x_k^{{}^{\prime }}}d{x}_k^{{}^{\prime }}-d{x}_i^{{}^{\prime }}d{x}_i^{{}^{\prime }}\\ & =\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}\frac{\partial x_i}{\partial x_k^{{}^{\prime }}}d{x}_j^{{}^{\prime }}d{x}_k^{{}^{\prime }}-d{x}_i^{{}^{\prime }}d{x}_i^{{}^{\prime }}\\ & =(\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}\frac{\partial x_i}{\partial x_k^{{}^{\prime }}}-{\delta }_{jk})d{x}_j^{{}^{\prime }}d{x}_k^{{}^{\prime }}\end{array}\text{\hspace{1em}(3.1)}$$
上式中括号中为度量线元变化的无量纲度量，将此取为应变度量，即格林应变
$$E_{ij}=\frac{1}{2}(\frac{\partial x_k}{\partial x_i^{{}^{\prime }}}\frac{\partial x_k}{\partial x_j^{{}^{\prime }}}-{\delta }_{ij})\text{\hspace{1em}(3.2)}$$
将其写成矩阵形式，如下所示
$$E=\frac{1}{2}(F^{T}F-I)\text{\hspace{1em}(3.3)}$$
格林应变以变形前的位形作为参考状态，同样可以用变形后的位形作为参考状态，那么线元前后的变化如下式所示

$$\begin{array}{rl}|\overrightarrow{oa}{|}^2-|\overrightarrow{OA}{|}^2& =d{x}_{i}d{x}_i-d{x}_i^{{}^{\prime }}d{x}_i^{{}^{\prime }}\\ & ={\delta }_{ij}d{x}_{i}d{x}_j-\frac{\partial x_i^{{}^{\prime }}}{\partial x_j}d{x}_j\cdot \frac{\partial x_i^{{}^{\prime }}}{\partial x_k}d{x}_k\\ & ={\delta }_{ij}d{x}_{i}d{x}_j-\frac{\partial x_i^{{}^{\prime }}}{\partial x_j}\frac{\partial x_i^{{}^{\prime }}}{\partial x_k}d{x}_{j}d{x}_k\\ & =({\delta }_{jk}-\frac{\partial x_i^{{}^{\prime }}}{\partial x_j}\frac{\partial x_i^{{}^{\prime }}}{\partial x_k})d{x}_{j}d{x}_k\end{array}\text{\hspace{1em}(3.4)}$$
定义应变度量，即阿尔曼西应变
$$e_{ij}=\frac{1}{2}({\delta }_{ij}-\frac{\partial x_k^{{}^{\prime }}}{\partial x_i}\frac{\partial x_k^{{}^{\prime }}}{\partial x_j})\text{\hspace{1em}(3.5)}$$
将其写成矩阵形式，如下所示
$$e=\frac{1}{2}(I-F^{-T}{F}^{-1})\text{\hspace{1em}(3.6)}$$

欧拉描述和拉格朗日描述的位移如下所示

$$\begin{gathered} u_i=x_i(x_j^{{}^{\prime }},t)-x_i^{{}^{\prime }} \\ {u}_i=x_i-x_i^{{}^{\prime }}(x_j,t)\text{\hspace{1em}(3.7)} \end{gathered}$$
如果用位移来表示上述两种应变，那么有
$$\begin{gathered} \frac{\partial u_i}{\partial x_j^{{}^{\prime }}}=\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}-{\delta }_{ij} \\ \frac{\partial u_i}{\partial x_j}={\delta }_{ij}-\frac{\partial x_i^{{}^{\prime }}}{\partial x_j}\text{\hspace{1em}(3.8)} \end{gathered}$$

将上式代入（3.2）式，可得
$$\begin{array}{rl}{E}_{ij}& =\frac{1}{2}(\frac{\partial x_k}{\partial x_i^{{}^{\prime }}}\frac{\partial x_k}{\partial x_j^{{}^{\prime }}}-{\delta }_{ij})\\ & =\frac{1}{2}[(\frac{\partial u_k}{\partial x_i^{{}^{\prime }}}+{\delta }_{ki})(\frac{\partial u_k}{\partial x_j^{{}^{\prime }}}+{\delta }_{kj})-{\delta }_{ij}]\\ & =\frac{1}{2}(\frac{\partial u_k}{\partial x_i^{{}^{\prime }}}\frac{\partial u_k}{\partial x_j^{{}^{\prime }}}+{\delta }_{ki}\frac{\partial u_k}{\partial x_j^{{}^{\prime }}}+{\delta }_{kj}\frac{\partial u_k}{\partial x_i^{{}^{\prime }}}+{\delta }_{ki}{\delta }_{kj}-{\delta }_{ij})\\ & =\frac{1}{2}(\frac{\partial u_k}{\partial x_i^{{}^{\prime }}}\frac{\partial u_k}{\partial x_j^{{}^{\prime }}}+\frac{\partial u_i}{\partial x_j^{{}^{\prime }}}+\frac{\partial u_j}{\partial x_i^{{}^{\prime }}})\end{array}\text{\hspace{1em}(3.9)}$$
将上式写成矩阵形式，此时需要引入哈密顿算子$\nabla$和张量积
$$\begin{gathered} \nabla u=\left[\begin{array}{c}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}\end{array}\right]\left[\begin{array}{ccc}{u}_x& u_y& u_z\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial u_x}{\partial x}& \frac{\partial u_y}{\partial x}& \frac{\partial u_z}{\partial x}\\ \frac{\partial u_x}{\partial y}& \frac{\partial u_y}{\partial y}& \frac{\partial u_z}{\partial y}\\ \frac{\partial u_x}{\partial z}& \frac{\partial u_y}{\partial z}& \frac{\partial u_z}{\partial z}\end{array}\right] \\ u\nabla =\left[\begin{array}{c}{u}_x\\ u_y\\ u_z\end{array}\right]\left[\begin{array}{ccc}\frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial u_x}{\partial x}& \frac{\partial u_x}{\partial y}& \frac{\partial u_x}{\partial z}\\ \frac{\partial u_y}{\partial x}& \frac{\partial u_y}{\partial y}& \frac{\partial u_y}{\partial z}\\ \frac{\partial u_z}{\partial x}& \frac{\partial u_z}{\partial y}& \frac{\partial u_z}{\partial z}\end{array}\right]\text{\hspace{1em}(3.10)} \end{gathered}$$
那么式（3.9）矩阵形式为
$$E=\frac{1}{2}({\nabla }_{0}u+u{\nabla }_0+{\nabla }_{0}u\cdot u{\nabla }_0)\text{\hspace{1em}(3.11)}$$
其中下标表示对初始坐标求微分。
将式（3.8）代入（3.5）式，可得
$$\begin{array}{rl}{e}_{ij}& =\frac{1}{2}({\delta }_{ij}-\frac{\partial x_k^{{}^{\prime }}}{\partial x_i}\frac{\partial x_k^{{}^{\prime }}}{\partial x_j})\\ & =\frac{1}{2}[{\delta }_{ij}-({\delta }_{ki}-\frac{\partial u_k}{\partial x_i})({\delta }_{kj}-\frac{\partial u_k}{\partial x_j})]\\ & =\frac{1}{2}({\delta }_{ij}-{\delta }_{ki}{\delta }_{kj}+{\delta }_{kj}\frac{\partial u_k}{\partial x_i}+{\delta }_{ki}\frac{\partial u_k}{\partial x_j}-\frac{\partial u_k}{\partial x_i}\frac{\partial u_k}{\partial x_j})\\ & =\frac{1}{2}(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j}-\frac{\partial u_k}{\partial x_i}\frac{\partial u_k}{\partial x_j})\end{array}\text{\hspace{1em}(3.12)}$$
那么式（3.12）矩阵形式为
$$e=\frac{1}{2}(\nabla u+u\nabla -\nabla u\cdot u\nabla )\text{\hspace{1em}(3.13)}$$

下面对格林应变和阿尔曼西应变进行一些讨论。
将式（3.1）式进行一些变化，原式
$$\begin{array}{rl}|\overrightarrow{oa}{|}^2-|\overrightarrow{OA}{|}^2& =2E_{ij}d{x}_i^{{}^{\prime }}d{x}_j^{{}^{\prime }}\end{array}\text{\hspace{1em}(3.14)}$$
令$ds=|\overrightarrow{oa}|$，$dS=|\overrightarrow{OA}|$，那么
$$d{s}^2-d{S}^2=2E_{ij}d{x}_i^{{}^{\prime }}d{x}_j^{{}^{\prime }}\text{\hspace{1em}(3.15)}$$
将上式左右各除$d{S}^2$，那么有
$$\begin{array}{rl}\frac{d{s}^2}{d{S}^2}-1& =2E_{ij}\frac{d{x}_i^{{}^{\prime }}}{dS}\frac{d{x}_j^{{}^{\prime }}}{dS}\\ & =2E_{ij}{\alpha }_i^{{}^{\prime }}{\alpha }_j^{{}^{\prime }}\end{array}\text{\hspace{1em}(3.16)}$$
其中${\alpha }_i^{{}^{\prime }}$为$\overrightarrow{OA}$单位化后的各分量。
在一维情况下，小应变为$ϵ=\frac{ds-dS}{dS}$，代入可得
$$(ϵ+1{)}^2=1+2E_{11}\to 2ϵ+{ϵ}^2=2E_{11}\text{\hspace{1em}(3.17)}$$

上述都是针对线应变，现在来讨论角应变，在讨论角应变时，式（3.1）就应该改为
$$\begin{array}{rl}|\overrightarrow{oa}|\cdot |\overrightarrow{ob}|-|\overrightarrow{OA}|\cdot |\overrightarrow{OB}|& =d{x}_i\delta x_i-d{x}_i^{{}^{\prime }}\delta x_i^{{}^{\prime }}\\ & =\frac{\partial x_i}{\partial x_j^{{}^{\prime }}}d{x}_j^{{}^{\prime }}\cdot \frac{\partial x_i}{\partial x_k^{{}^{\prime }}}\delta x_k^{{}^{\prime }}-d{x}_i^{{}^{\prime }}\delta x_i^{{}^{\prime }}\\ & =\frac{\partial x_m}{\partial x_i^{{}^{\prime }}}\frac{\partial x_m}{\partial x_j^{{}^{\prime }}}d{x}_i^{{}^{\prime }}\delta x_j^{{}^{\prime }}-d{x}_i^{{}^{\prime }}\delta x_i^{{}^{\prime }}\\ & =(\frac{\partial x_m}{\partial x_i^{{}^{\prime }}}\frac{\partial x_m}{\partial x_j^{{}^{\prime }}}-{\delta }_{ij})d{x}_i^{{}^{\prime }}\delta x_j^{{}^{\prime }}\\ & =2E_{ij}d{x}_i^{{}^{\prime }}\delta x_j^{{}^{\prime }}\end{array}\text{\hspace{1em}(3.1’)}$$
上式进一步改为
$$\begin{array}{rl}|\overrightarrow{oa}|\cdot |\overrightarrow{ob}|-|\overrightarrow{OA}|\cdot |\overrightarrow{OB}|& =ds\delta s\cos \theta -dS\delta S\cos {\theta }_0\\ & =2E_{ij}d{x}_i^{{}^{\prime }}\delta x_j^{{}^{\prime }}\end{array}\text{\hspace{1em}(3.18)}$$
上式两端除以$dS\delta S$，同时${\theta }_0=\frac{\pi }{2}$，${\alpha }_i=\frac{d{x}_i^{{}^{\prime }}}{dS}$，${\alpha }_j=\frac{\delta x_j^{{}^{\prime }}}{\delta S}$，因此上式改为
$$\begin{array}{rl}\frac{ds}{dS}\frac{\delta s}{\delta S}\cos \theta -\cos {\theta }_0& =\frac{ds}{dS}\frac{\delta s}{\delta S}\cos \theta \\ & ={\lambda }^a{\lambda }^b\sin {\theta }_{ab}\\ & =2E_{ij}{\alpha }_i{\alpha }_j\end{array}\text{\hspace{1em}(3.19)}$$
其中$\sin {\theta }_{ab}=\frac{\pi }{2}-\theta$即为角应变，由下式确定
$$\sin {\theta }_{ab}=\frac{2E_{ij}{\alpha }_i{\alpha }_j}{{\lambda }^a{\lambda }^b}\text{\hspace{1em}(3.20)}$$
格林应变张量中的$E_{ij}$与角应变的关系中还包含线伸长量，因此不想小应变假设中的${\gamma }_{ij}$这么简单。