Python 机器学习 基础 之 模型评估与改进 【评估指标与评分】的简单说明
目录
Python 机器学习 基础 之 模型评估与改进 【评估指标与评分】的简单说明
一、简单介绍
二、评估指标与评分
1)错误类型
2)不平衡数据集
3)混淆矩阵
4)考虑不确定性
5)准确率-召回率曲线
6)受试者工作特征(ROC)与AUC
4、回归指标
附录
一、参考文献
一、简单介绍
Python是一种跨平台的计算机程序设计语言。是一种面向对象的动态类型语言,最初被设计用于编写自动化脚本(shell),随着版本的不断更新和语言新功能的添加,越多被用于独立的、大型项目的开发。Python是一种解释型脚本语言,可以应用于以下领域: Web 和 Internet开发、科学计算和统计、人工智能、教育、桌面界面开发、软件开发、后端开发、网络爬虫。
Python 机器学习是利用 Python 编程语言中的各种工具和库来实现机器学习算法和技术的过程。Python 是一种功能强大且易于学习和使用的编程语言,因此成为了机器学习领域的首选语言之一。Python 提供了丰富的机器学习库,如Scikit-learn、TensorFlow、Keras、PyTorch等,这些库包含了许多常用的机器学习算法和深度学习框架,使得开发者能够快速实现、测试和部署各种机器学习模型。
Python 机器学习涵盖了许多任务和技术,包括但不限于:
- 监督学习:包括分类、回归等任务。
- 无监督学习:如聚类、降维等。
- 半监督学习:结合了有监督和无监督学习的技术。
- 强化学习:通过与环境的交互学习来优化决策策略。
- 深度学习:利用深度神经网络进行学习和预测。
通过 Python 进行机器学习,开发者可以利用其丰富的工具和库来处理数据、构建模型、评估模型性能,并将模型部署到实际应用中。Python 的易用性和庞大的社区支持使得机器学习在各个领域都得到了广泛的应用和发展。
二、评估指标与评分
使用精度(正确分类的样本所占的比例)来评估分类性能,使用 来评估回归性能。但是,总结监督模型在给定数据集上的表现有多种方法,这两个指标只是其中两种。在实践中,这些评估指标可能不适用于你的应用。在选择模型与调参时,选择正确的指标是很重要的。
在机器学习中,评估指标和评分方法是用来衡量模型性能的工具。这些工具可以帮助你理解模型在不同任务上的表现,并对比不同模型或相同模型在不同参数设置下的优劣。评估指标和评分方法因具体任务而异,比如分类、回归或聚类任务。以下是一些常见的评估指标和评分方法:
分类任务的评估指标
准确率 (Accuracy):
- 定义:模型预测正确的样本占总样本的比例。
- 适用场景:适用于样本类别分布均衡的场景。
精确率 (Precision):
- 定义:模型预测为正类的样本中实际为正类的比例。
- 适用场景:适用于关注正类预测准确性的场景,例如垃圾邮件检测。
召回率 (Recall):
- 定义:实际为正类的样本中被模型正确预测为正类的比例。
- 适用场景:适用于关注正类样本全部被识别出来的场景,例如疾病检测。
F1-score:
- 定义:精确率和召回率的调和平均数。
- 适用场景:适用于需要在精确率和召回率之间找到平衡的场景。
ROC曲线和AUC (Receiver Operating Characteristic Curve and Area Under the Curve):
- 定义:ROC曲线显示了不同阈值下的假正例率和真正例率,AUC则是ROC曲线下的面积。
- 适用场景:适用于评估模型区分正负样本能力的场景。
回归任务的评估指标
均方误差 (Mean Squared Error, MSE):
- 定义:预测值与真实值之间差异的平方的平均数。
- 适用场景:适用于希望严重惩罚大偏差的场景。
均方根误差 (Root Mean Squared Error, RMSE):
- 定义:均方误差的平方根。
- 适用场景:与MSE相似,但更直观,因为与原始值单位相同。
平均绝对误差 (Mean Absolute Error, MAE):
- 定义:预测值与真实值之间差异的绝对值的平均数。
- 适用场景:适用于希望均衡处理所有偏差的场景。
R² (决定系数):
- 定义:解释了自变量在因变量中的变异比例。
- 适用场景:适用于评估模型对数据的解释能力的场景。
聚类任务的评估指标
轮廓系数 (Silhouette Score):
- 定义:衡量样本在其所属簇中的紧密度和与最近簇的分离度。
- 适用场景:适用于评估聚类质量的场景。
互信息 (Mutual Information):
- 定义:度量两个变量之间的互信息量。
- 适用场景:适用于评估聚类结果与真实标签的相关性。
调整兰德指数 (Adjusted Rand Index, ARI):
- 定义:衡量聚类结果与真实标签的相似性,调整了随机聚类结果的期望值。
- 适用场景:适用于评估聚类结果质量的场景。
选择评估指标和评分方法时,应该根据具体任务的需求和关注点来决定。例如,对于分类任务,如果关注的是模型对正类样本的识别能力,可以选择精确率、召回率和F1-score;对于回归任务,如果希望惩罚大偏差,可以选择均方误差或均方根误差。通过合适的评估指标和评分方法,可以更准确地理解模型性能,从而进行更有效的模型优化和选择。
1、牢记最终目标
在选择指标时,你应该始终牢记机器学习应用的最终目标。在实践中,我们通常不仅对精确的预测感兴趣,还希望将这些预测结果用于更大的决策过程。在选择机器学习指标之前,你应该考虑应用的高级目标,这通常被称为商业指标 (business metric)。对于一个机器学习应用,选择特定算法的结果被称为商业影响 (business impact)(请具有科学头脑的读者原谅本节中出现的商业语言。不忘最终目标在科学中也同样重要,但作者想不到在这一领域中与“商业影响”具有类似含义的词语)。 高级目标可能是避免交通事故或者减少入院人数,也可能是吸引更多的网站用户或者让用户在你的商店中花更多的钱。在选择模型或调参时,你应该选择对商业指标具有最大正面影响的模型或参数值。这通常是很难的,因为要想评估某个模型的商业影响,可能需要将它放在真实的生产环境中。
在开发的初期阶段调参,仅为了测试就将模型投入生产环境往往是不可行的,因为可能涉及很高的商业风险或个人风险。想象一下,为了测试无人驾驶汽车的行人避让能力,没有事先验证就让它直接上路。如果模型很糟糕的话,行人就会遇到麻烦!因此,我们通常需要找到某种替代的评估程序,使用一种更容易计算的评估指标。例如,我们可以测试对行人和非行人的图片进行分类并测量精度。请记住,这只是一种替代方法,找到与原始商业目标最接近的可评估的指标也很有用。应尽可能使用这个最接近的指标来进行模型评估与选择。评估的结果可能不是一个数字——算法的结果可能是顾客多了 10%,但每位顾客的花费减少了 15%——但它应该给出选择一个模型而不选另一个所造成的预期商业影响。
2、二分类指标
二分类可能是实践中最常见的机器学习应用,也是概念最简单的应用。但是,即使是评估这个简单任务也仍有一些注意事项。在深入研究替代指标之前,我们先看一下测量精度可能会如何误导我们。请记住,对于二分类问题,我们通常会说正类 (positive class)和反类 (negative class),而正类是我们要寻找的类。
1)错误类型
通常来说,精度并不能很好地度量预测性能,因为我们所犯错误的数量并不包含我们感兴趣的所有信息。想象一个应用,利用自动化测试来筛查癌症的早期发现。如果测试结果为阴性,那么认为患者是健康的,而如果测试结果为阳性,患者则需要接受额外的筛查。这里我们将阳性测试结果(表示患有癌症)称为正类,将阴性测试结果称为反类。我们不能假设模型永远是完美的,它也会犯错。对于任何应用而言,我们都需要问问自己,这些错误在现实世界中可能有什么后果。
一种可能的错误是健康的患者被诊断为阳性,导致需要进行额外的测试。这给患者带来了一些费用支出和不便(可能还有精神上的痛苦)。错误的阳性预测叫作假正例 (false positive)。另一种可能的错误是患病的人被诊断为阴性,因而不会接受进一步的检查和治疗。未诊断出的癌症可能导致严重的健康问题,甚至可能致命。这种类型的错误(错误的阴性预测)叫作假反例 (false negative)。在统计学中,假正例也叫作第一类错误 (type I error),假反例也叫作第二类错误 (type II error)。我们将坚持使用“假正例”和“假反例”的说法,因为它们的含义更加明确,也更好记。在癌症诊断的例子中,显然,我们希望尽量避免假反例,而假正例可以被看作是小麻烦。
虽然这是一个特别极端的例子,但假正例和假反例造成的结果很少相同。在商业应用中,可以为两种类型的错误分配美元值,即用美元而不是精度来度量某个预测结果的错误。对于选择使用哪种模型的商业决策而言,这种方法可能更有意义。
2)不平衡数据集
如果在两个类别中,一个类别的出现次数比另一个多很多,那么错误类型将发挥重要作用。这在实践中十分常见,一个很好的例子是点击(click-through)预测,其中每个数据点表示一个“印象”(impression),即向用户展示的一个物项。这个物项可能是广告、相关的故事,或者是在社交媒体网站上关注的相关人员。目标是预测用户是否会点击看到的某个特定物项(表示他们感兴趣)。用户对互联网上显示的大多数内容(尤其是广告)都不会点击。你可能需要向用户展示 100 个广告或文章,他们才会找到足够有趣的内容来点击查看。这样就会得到一个数据集,其中每 99 个“未点击”的数据点才有 1 个“已点击”的数据点。换句话说,99% 的样本属于“未点击”类别。这种一个类别比另一个类别出现次数多很多的数据集,通常叫作不平衡数据集 (imbalanced dataset)或者具有不平衡类别的数据集 (dataset with imbalanced classes)。在实际当中,不平衡数据才是常态,而数据中感兴趣事件的出现次数相同或相似的情况十分罕见。
现在假设你在构建了一个在点击预测任务中精度达到 99% 的分类器。这告诉了你什么?99% 的精度听起来令人印象深刻,但是它并没有考虑类别不平衡。你不必构建机器学习模型,始终预测“未点击”就可以得到 99% 的精度。另一方面,即使是不平衡数据,精度达到 99% 的模型实际上也是相当不错的。但是,精度无法帮助我们区分不变的“未点击”模型与潜在的优秀模型。
为了便于说明,我们将 digits 数据集中的数字 9 与其他九个类别加以区分,从而创建一个 9:1 的不平衡数据集:
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits = load_digits()
y = digits.target == 9
X_train, X_test, y_train, y_test = train_test_split(
digits.data, y, random_state=0)我们可以使用 DummyClassifier 来始终预测多数类(这里是“非 9”),以查看精度提供的信息量有多么少:
from sklearn.dummy import DummyClassifier
import numpy as np
dummy_majority = DummyClassifier(strategy='most_frequent').fit(X_train, y_train)
pred_most_frequent = dummy_majority.predict(X_test)
print("Unique predicted labels: {}".format(np.unique(pred_most_frequent)))
print("Test score: {:.2f}".format(dummy_majority.score(X_test, y_test)))Unique predicted labels: [False] Test score: 0.90
我们得到了接近 90% 的精度,却没有学到任何内容。这个结果可能看起来相当好,但请思考一会儿。想象一下,有人告诉你他们的模型精度达到 90%。你可能会认为他们做得很好。但根据具体问题,也可能是仅预测了一个类别!我们将这个结果与使用一个真实分类器的结果进行对比:
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=2).fit(X_train, y_train)
pred_tree = tree.predict(X_test)
print("Test score: {:.2f}".format(tree.score(X_test, y_test)))Test score: 0.92
从精度来看,DecisionTreeClassifier 仅比常数预测稍好一点。这可能表示我们使用 DecisionTreeClassifier 的方法有误,也可能是因为精度实际上在这里不是一个很好的度量。
为了便于对比,我们再评估两个分类器,LogisticRegression 与默认的 DummyClassifier ,其中后者进行随机预测,但预测类别的比例与训练集中的比例相同:
from sklearn.linear_model import LogisticRegression
dummy = DummyClassifier().fit(X_train, y_train)
pred_dummy = dummy.predict(X_test)
print("dummy score: {:.2f}".format(dummy.score(X_test, y_test)))
logreg = LogisticRegression(C=0.1).fit(X_train, y_train)
pred_logreg = logreg.predict(X_test)
print("logreg score: {:.2f}".format(logreg.score(X_test, y_test)))dummy score: 0.90 logreg score: 0.98
显而易见,产生随机输出的虚拟分类器是所有分类器中最差的(精度最低),而 LogisticRegression 则给出了非常好的结果。但是,即使是随机分类器也得到了超过 80% 的精度。这样很难判断哪些结果是真正有帮助的。这里的问题在于,要想对这种不平衡数据的预测性能进行量化,精度并不是一种合适的度量。在本章接下来的内容中,我们将探索在选择模型方面能够提供更好指导的其他指标。我们特别希望有一个指标可以告诉我们,一个模型比“最常见”预测(由 pred_most_frequent 给出)或随机预测(由 pred_dummy 给出)要好多少。如果我们用一个指标来评估模型,那么这个指标应该能够淘汰这些无意义的预测。
3)混淆矩阵
对于二分类问题的评估结果,一种最全面的表示方法是使用混淆矩阵(confusion matrix)。我们利用 confusion_matrix 函数来检查上一节中 LogisticRegression 的预测结果。我们已经将测试集上的预测结果保存在 pred_logreg 中:
from sklearn.metrics import confusion_matrix
confusion = confusion_matrix(y_test, pred_logreg)
print("Confusion matrix:\n{}".format(confusion))Confusion matrix: [[402 1] [ 6 41]]
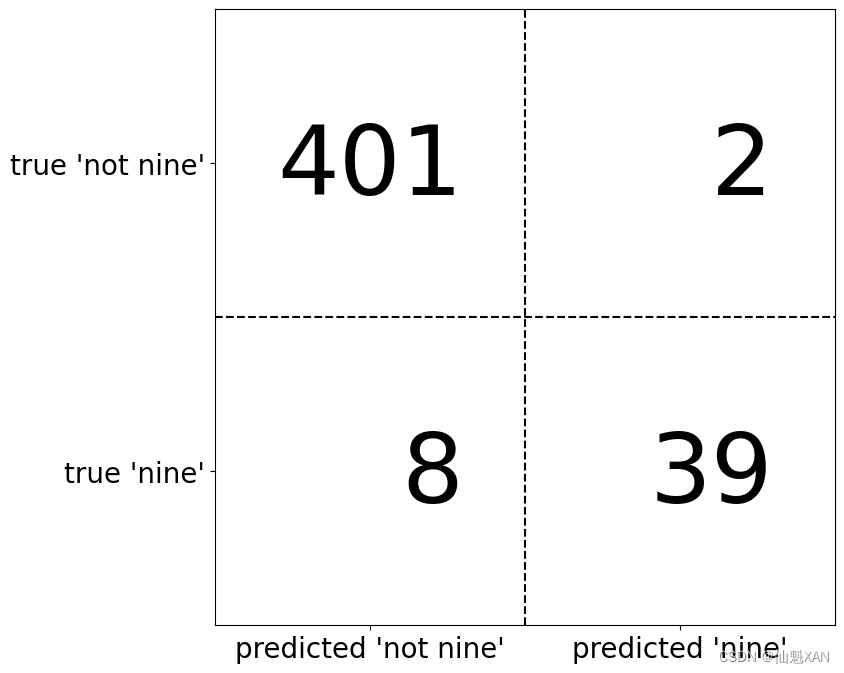
confusion_matrix 的输出是一个 2×2 数组,其中行对应于真实的类别,列对应于预测的类别。数组中每个元素给出属于该行对应类别(这里是“非 9”和“9”)的样本被分类到该列对应类别中的数量。图 5-10 对这一含义进行了说明。
import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_confusion_matrix_illustration()
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-01.png', bbox_inches='tight')
plt.show()混淆矩阵主对角线上的元素对应于正确的分类,而其他元素则告诉我们一个类别中有多少样本被错误地划分到其他类别中。
如果我们将“9”作为正类,那么就可以将混淆矩阵的元素与前面介绍过的假正例 (false positive)和假反例 (false negative)两个术语联系起来。为了使图像更加完整,我们将正类中正确分类的样本称为真正例 (true positive),将反类中正确分类的样本称为真反例 (true negative)。这些术语通常缩写为 FP、FN、TP 和 TN,这样就可以得到下图对混淆矩阵的解释(图 5-11):
mglearn.plots.plot_binary_confusion_matrix()
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-02.png', bbox_inches='tight')
plt.show()
下面我们用混淆矩阵来比较前面拟合过的模型(两个虚拟模型、决策树和 Logistic 回归):
print("Most frequent class:")
print(confusion_matrix(y_test, pred_most_frequent))
print("\nDummy model:")
print(confusion_matrix(y_test, pred_dummy))
print("\nDecision tree:")
print(confusion_matrix(y_test, pred_tree))
print("\nLogistic Regression")
print(confusion_matrix(y_test, pred_logreg))Most frequent class: [[403 0] [ 47 0]] Dummy model: [[403 0] [ 47 0]] Decision tree: [[390 13] [ 24 23]] Logistic Regression [[402 1] [ 6 41]]
观察混淆矩阵,很明显可以看出 pred_most_frequent 有问题,因为它总是预测同一个类别。另一方面,pred_dummy 的真正例数量很少(4 个),特别是与假反例和假正例的数量相比——假正例的数量竟然比真正例还多!决策树的预测比虚拟预测更有意义,即使二者精度几乎相同。最后,我们可以看到,Logistic 回归在各方面都比 pred_tree 要好:它的真正例和真反例的数量更多,而假正例和假反例的数量更少。从这个对比中可以明确看出,只有决策树和 Logistic 回归给出了合理的结果,并且 Logistic 回归的效果全面好于决策树。但是,检查整个混淆矩阵有点麻烦,虽然我们通过观察矩阵的各个方面得到了很多深入见解,但是这个过程是人工完成的,也是非常定性的。有几种方法可以总结混淆矩阵中包含的信息,我们将在后面进行讨论。
与精度的关系 。我们已经讲过一种总结混淆矩阵结果的方法——计算精度,其公式表达如下所示:
![]()
换句话说,精度是正确预测的数量(TP 和 TN)除以所有样本的数量(混淆矩阵中所有元素的总和)。
准确率、召回率与 f -分数 。总结混淆矩阵还有几种方法,其中最常见的就是准确率和召回率。准确率 (precision)度量的是被预测为正例的样本中有多少是真正的正例:
![]()
如果目标是限制假正例的数量,那么可以使用准确率作为性能指标。举个例子,想象一个模型,它预测一种新药在临床试验治疗中是否有效。众所周知,临床试验非常昂贵,制药公司只有在非常确定药物有效的情况下才会进行试验。因此,模型不会产生很多假正例是很重要的——换句话说,模型的准确率很高。准确率也被称为阳性预测值 (positive predictive value,PPV)。
另一方面,召回率 (recall)度量的是正类样本中有多少被预测为正类:
![]()
如果我们需要找出所有的正类样本,即避免假反例是很重要的情况下,那么可以使用召回率作为性能指标。本章前面的癌症诊断例子就是一个很好的例子:找出所有患病的人很重要,预测结果中可能包含健康的人。召回率的其他名称有灵敏度 (sensitivity)、命中率 (hit rate)和真正例率 (true positive rate,TPR)。
在优化召回率与优化准确率之间需要折中。如果你预测所有样本都属于正类,那么可以轻松得到完美的召回率——没有假反例,也没有真反例。但是,将所有样本都预测为正类,将会得到许多假正例,因此准确率会很低。与之相反,如果你的模型只将一个最确定的数据点预测为正类,其他点都预测为反类,那么准确率将会很完美(假设这个数据点实际上就属于正类),但是召回率会非常差。
准确率和召回率只是从 TP、FP、TN 和 FN 导出的众多分类度量中的两个。你可以在 Wikipedia 上找到所有度量的摘要(https://en.wikipedia.org/wiki/Sensitivity_and_specificity )。在机器学习社区中,准确率和召回率是最常用的二分类度量,但其他社区可能使用其他相关指标。
虽然准确率和召回率是非常重要的度量,但是仅查看二者之一无法为你提供完整的图景。将两种度量进行汇总的一种方法是 f -分数 (f -score)或 f -度量 (f -measure),它是准确率与召回率的调和平均:
![]()
这一特定变体也被称为 f 1 -分数 (f 1 -score)。由于同时考虑了准确率和召回率,所以它对于不平衡的二分类数据集来说是一种比精度更好的度量。我们对之前计算过的“9 与其余”数据集的预测结果计算 f 1 -分数。这里我们假定“9”类是正类(标记为 True ,其他样本被标记为 False ),因此正类是少数类:
from sklearn.metrics import f1_score
print("f1 score most frequent: {:.2f}".format(
f1_score(y_test, pred_most_frequent)))
print("f1 score dummy: {:.2f}".format(f1_score(y_test, pred_dummy)))
print("f1 score tree: {:.2f}".format(f1_score(y_test, pred_tree)))
print("f1 score logistic regression: {:.2f}".format(
f1_score(y_test, pred_logreg)))f1 score most frequent: 0.00 f1 score dummy: 0.00 f1 score tree: 0.55 f1 score logistic regression: 0.92
这里我们可以注意到两件事情。第一,我们从 most_frequent 的预测中得到一条错误信息,因为预测的正类数量为 0(使得 f -分数的分母为 0)。第二,我们可以看到虚拟预测与决策树预测之间有很大的区别,而仅观察精度时二者的区别并不明显。利用 f -分数进行评估,我们再次用一个数字总结了预测性能。但是,f -分数似乎比精度更加符合我们对好模型的直觉。然而,f -分数的一个缺点是比精度更加难以解释。
如果我们想要对准确率、召回率和 f 1 -分数做一个更全面的总结,可以使用 classification_report 这个很方便的函数,它可以同时计算这三个值,并以美观的格式打印出来:
from sklearn.metrics import classification_report
print(classification_report(y_test, pred_most_frequent,
target_names=["not nine", "nine"])) precision recall f1-score support
not nine 0.90 1.00 0.94 403
nine 0.00 0.00 0.00 47
accuracy 0.90 450
macro avg 0.45 0.50 0.47 450
weighted avg 0.80 0.90 0.85 450
classification_report 函数为每个类别(这里是 True 和 False )生成一行,并给出以该类别作为正类的准确率、召回率和 f -分数。前面我们假设较少的“9”类是正类。如果将正类改为“not nine”(非 9),我们可以从 classification_report 的输出中看出,利用 most_frequent 模型得到的 f -分数为 0.94。此外,对于“not nine”类别,召回率是 1,因为我们将所有样本都分类为“not nine”。f -分数旁边的最后一列给出了每个类别的支持 (support),它表示的是在这个类别中真实样本的数量。
分类报告的最后一行显示的是对应指标的加权平均(按每个类别中的样本个数加权)。下面还有两个报告,一个是虚拟分类器的 7 ,一个是 Logistic 回归的:
print(classification_report(y_test, pred_dummy,
target_names=["not nine", "nine"])) precision recall f1-score support
not nine 0.90 1.00 0.94 403
nine 0.00 0.00 0.00 47
accuracy 0.90 450
macro avg 0.45 0.50 0.47 450
weighted avg 0.80 0.90 0.85 450
print(classification_report(y_test, pred_logreg, target_names=["not nine", "nine"])) precision recall f1-score support
not nine 0.99 1.00 0.99 403
nine 0.98 0.87 0.92 47
accuracy 0.98 450
macro avg 0.98 0.93 0.96 450
weighted avg 0.98 0.98 0.98 450
在查看报告时你可能注意到了,虚拟模型与好模型之间的区别不再那么明显。选择哪个类作为正类对指标有很大影响。虽然在以“nine”类作为正类时虚拟分类的 f -分数是 0.10(对比 Logistic 回归的 0.89),而以“not nine”类作为正类时二者的 f -分数分别是 0.91 和 0.99,两个结果看起来都很合理。不过同时查看所有数字可以给出非常准确的图像,我们可以清楚地看到 Logistic 回归模型的优势。
4)考虑不确定性
混淆矩阵和分类报告为一组特定的预测提供了非常详细的分析。但是,预测本身已经丢弃了模型中包含的大量信息。正如我们在第 2 章中所讨论的那样,大多数分类器都提供了一个 decision_function 或 predict_proba 方法来评估预测的不确定度。预测可以被看作是以某个固定点作为 decision_function 或 predict_proba 输出的阈值——在二分类问题中,我们使用 0 作为决策函数的阈值,0.5 作为 predict_proba 的阈值。
下面是一个不平衡二分类任务的示例,反类中有 400 个点,而正类中只有 50 个点。训练数据如图 5-12 左侧所示。我们在这个数据上训练一个核 SVM 模型,训练数据右侧的图像将决策函数值绘制为热图。你可以在图像偏上的位置看到一个黑色圆圈,表示 decision_function 的阈值刚好为 0。在这个圆圈内的点将被划为正类,圆圈外的点将被划为反类:
from mglearn.datasets import make_blobs
from sklearn.svm import SVC
# 定义两个中心点
centers = [[-5, 0], [5, 0]]
# 生成数据
X, y = make_blobs(n_samples=(400, 50), centers=centers, cluster_std=[7.0, 2], random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma=.05).fit(X_train, y_train)mglearn.plots.plot_decision_threshold()
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-03.png', bbox_inches='tight')
plt.show()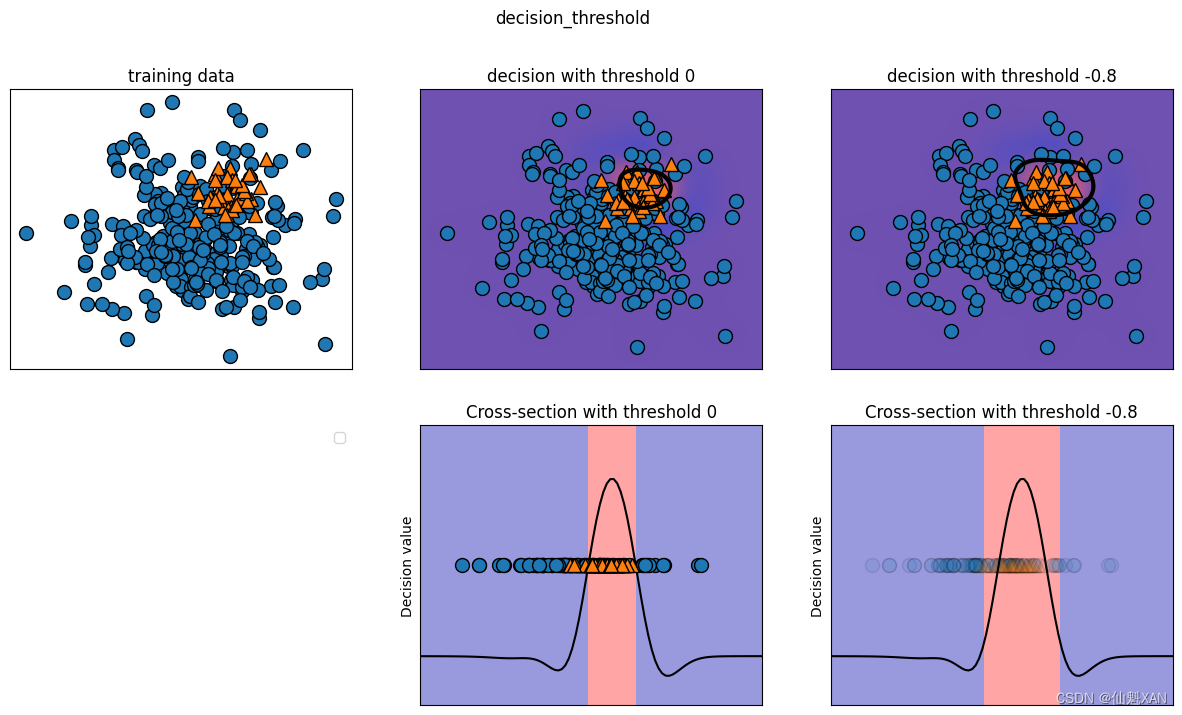
我们可以使用 classification_report 函数来评估两个类别的准确率与召回率:
print(classification_report(y_test, svc.predict(X_test))) precision recall f1-score support
0 0.93 0.96 0.94 96
1 0.71 0.59 0.65 17
accuracy 0.90 113
macro avg 0.82 0.77 0.79 113
weighted avg 0.90 0.90 0.90 113
对于类别 1,我们得到了一个相当低的准确率,而召回率则令人糊涂(mixed)。由于类别 0 要大得多,所以分类器将重点放在将类别 0 分类正确,而不是较小的类别 1。
假设在我们的应用中,类别 1 具有高召回率更加重要,正如前面的癌症筛查例子那样。这意味着我们愿意冒险有更多的假正例(假的类别 1),以换取更多的真正例(可增大召回率)。svc.predict 生成的预测无法满足这个要求,但我们可以通过改变决策阈值不等于 0 来将预测重点放在使类别 1 的召回率更高。默认情况下,decision_function 值大于 0 的点将被划为类别 1。我们希望将更多 的点划为类别 1,所以需要减小 阈值:
print(classification_report(y_test, y_pred_lower_threshold)) precision recall f1-score support
0 0.97 0.95 0.96 96
1 0.74 0.82 0.78 17
accuracy 0.93 113
macro avg 0.85 0.89 0.87 113
weighted avg 0.93 0.93 0.93 113
正如所料,类别 1 的召回率增大,准确率减小。现在我们将更大的空间区域划为类别 1,正如图 5-12 右上图中所示。如果你认为准确率比召回率更重要,或者反过来,或者你的数据严重不平衡,那么改变决策阈值是得到更好结果的最简单方法。由于 decision_function 的取值可能在任意范围,所以很难提供关于如何选取阈值的经验法则。
如果你设置了阈值,那么要小心不要在测试集上这么做。与其他任何参数一样,在测试集上设置决策阈值可能会得到过于乐观的结果。可以使用验证集或交叉验证来代替。
对于实现了 predict_proba 方法的模型来说,选择阈值可能更简单,因为 predict_proba 的输出固定在 0 到 1 的范围内,表示的是概率。默认情况下,0.5 的阈值表示,如果模型以超过 50% 的概率“确信”一个点属于正类,那么就将其划为正类。增大这个阈值意味着模型需要更加确信才能做出正类的判断(较低程度的确信就可以做出反类的判断)。虽然使用概率可能比使用任意阈值更加直观,但并非所有模型都提供了不确定性的实际模型(一棵生长到最大深度的 DecisionTree 总是 100% 确信其判断,即使很可能是错的)。这与校准(calibration)的概念相关:校准模型是指能够为其不确定性提供精确度量的模型。校准的详细讨论超出了本书的范围,但你可以在 Alexandru Niculescu-Mizil 和 Rich Caruana 的“Predicting Good Probabilities with Supervised Learning”(http://www.machinelearning.org/proceedings/icml2005/papers/079_GoodProbabilities_NiculescuMizilCaruana.pdf )这篇文章中找到更多内容。
5)准确率-召回率曲线
如前所述,改变模型中用于做出分类决策的阈值,是一种调节给定分类器的准确率和召回率之间折中的方法。你可能希望仅遗漏不到 10% 的正类样本,即希望召回率能达到 90%。这一决策取决于应用,应该是由商业目标驱动的。一旦设定了一个具体目标(比如对某一类别的特定召回率或准确率),就可以适当地设定一个阈值。总是可以设置一个阈值来满足特定的目标,比如 90% 的召回率。难点在于开发一个模型,在满足这个阈值的同时仍具有合理的准确率——如果你将所有样本都划为正类,那么将会得到 100% 的召回率,但你的模型毫无用处。
对分类器设置要求(比如 90% 的召回率)通常被称为设置工作点 (operating point)。在业务中固定工作点通常有助于为客户或组织内的其他小组提供性能保证。
在开发新模型时,通常并不完全清楚工作点在哪里。因此,为了更好地理解建模问题,很有启发性的做法是,同时 查看所有可能的阈值或准确率和召回率的所有可能折中。利用一种叫作准确率 - 召回率曲线 (precision-recall curve)的工具可以做到这一点。你可以在 sklearn.metrics 模块中找到计算准确率 - 召回率曲线的函数。这个函数需要真实标签与预测的不确定度,后者由 decision_function 或 predict_proba 给出:
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(
y_test, svc.decision_function(X_test))precision_recall_curve 函数返回一个列表,包含按顺序排序的所有可能阈值(在决策函数中出现的所有值)对应的准确率和召回率,这样我们就可以绘制一条曲线,如图 5-13 所示:
# 定义两个中心点
centers = [[-5, 0], [5, 0]]
# 使用更多数据点来得到更加平滑的曲线
X, y = make_blobs(n_samples=(4000, 500), centers=centers, cluster_std=[7.0, 2],
random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma=.05).fit(X_train, y_train)
precision, recall, thresholds = precision_recall_curve(
y_test, svc.decision_function(X_test))
# 找到最接近于0的阈值
close_zero = np.argmin(np.abs(thresholds))
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.plot(precision, recall, label="precision recall curve")
plt.xlabel("Precision")
plt.ylabel("Recall")
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-04.png', bbox_inches='tight')
plt.show()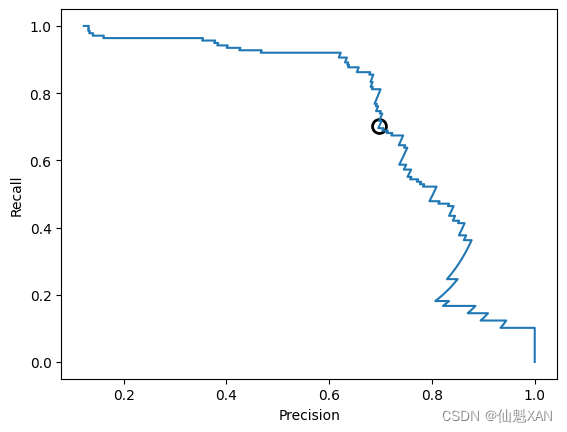
图 5-13 中曲线上的每一个点都对应 decision_function 的一个可能的阈值。例如,我们可以看到,在准确率约为 0.75 的位置对应的召回率为 0.4。黑色圆圈表示的是阈值为 0 的点,0 是 decision_function 的默认阈值。这个点是在调用 predict 方法时所选择的折中点。
曲线越靠近右上角,则分类器越好。右上角的点表示对于同一个阈值,准确率和召回率都很高。曲线从左上角开始,这里对应于非常低的阈值,将所有样本都划为正类。提高阈值可以让曲线向准确率更高的方向移动,但同时召回率降低。继续增大阈值,大多数被划为正类的点都是真正例,此时准确率很高,但召回率更低。随着准确率的升高,模型越能够保持较高的召回率,则模型越好。
进一步观察这条曲线,可以发现,利用这个模型可以得到约 0.5 的准确率,同时保持很高的召回率。如果我们想要更高的准确率,那么就必须牺牲很多召回率。换句话说,曲线左侧相对平坦,说明在准确率提高的同时召回率没有下降很多。当准确率大于 0.5 之后,准确率每增加一点都会导致召回率下降许多。
不同的分类器可能在曲线上不同的位置(即在不同的工作点)表现很好。我们来比较一下在同一数据集上训练的 SVM 与随机森林。RandomForestClassifier 没有 decision_function ,只有 predict_proba 。precision_recall_curve 函数的第二个参数应该是正类(类别 1)的确定性度量,所以我们传入样本属于类别 1 的概率(即 rf.predict_proba(X_test)[:, 1] )。二分类问题的 predict_proba 的默认阈值是 0.5,所以我们在曲线上标出这个点(见图 5-14):
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100, random_state=0, max_features=2)
rf.fit(X_train, y_train)
# RandomForestClassifier有predict_proba,但没有decision_function
precision_rf, recall_rf, thresholds_rf = precision_recall_curve(
y_test, rf.predict_proba(X_test)[:, 1])
plt.plot(precision, recall, label="svc")
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10,
label="threshold zero svc", fillstyle="none", c='k', mew=2)
plt.plot(precision_rf, recall_rf, label="rf")
close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5))
plt.plot(precision_rf[close_default_rf], recall_rf[close_default_rf], '^', c='k',
markersize=10, label="threshold 0.5 rf", fillstyle="none", mew=2)
plt.xlabel("Precision")
plt.ylabel("Recall")
plt.legend(loc="best")
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-05.png', bbox_inches='tight')
plt.show()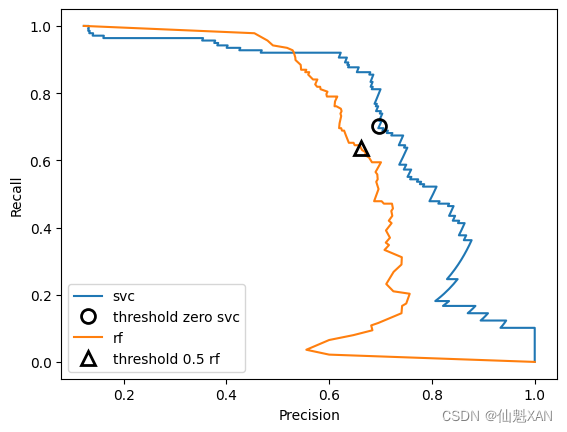
从这张对比图中可以看出,随机森林在极值处(要求很高的召回率或很高的准确率)的表现更好。在中间位置(准确率约为 0.7)SVM 的表现更好。如果我们只查看 f 1 -分数来比较二者的总体性能,那么可能会遗漏这些细节。f 1 -分数只反映了准确率 - 召回率曲线上的一个点,即默认阈值对应的那个点:
print("f1_score of random forest: {:.3f}".format(
f1_score(y_test, rf.predict(X_test))))
print("f1_score of svc: {:.3f}".format(f1_score(y_test, svc.predict(X_test))))f1_score of random forest: 0.647 f1_score of svc: 0.700
比较这两条准确率 - 召回率曲线,可以为我们提供大量详细的洞见,但这是一个相当麻烦的过程。对于自动化模型对比,我们可能希望总结曲线中包含的信息,而不限于某个特定的阈值或工作点。总结准确率 - 召回率曲线的一种方法是计算该曲线下的积分或面积,也叫作 平均准确率 (average precision)。8 你可以使用 average_precision_score 函数来计算平均准确率。因为我们要计算准确率 - 召回率曲线并考虑多个阈值,所以需要向 average_precision_score 传入 decision_function 或 predict_proba 的结果,而不是 predict 的结果:
from sklearn.metrics import average_precision_score
ap_rf = average_precision_score(y_test, rf.predict_proba(X_test)[:, 1])
ap_svc = average_precision_score(y_test, svc.decision_function(X_test))
print("Average precision of random forest: {:.3f}".format(ap_rf))
print("Average precision of svc: {:.3f}".format(ap_svc))
Average precision of random forest: 0.645 Average precision of svc: 0.765
在对所有可能的阈值进行平均时,我们看到随机森林和 SVC 的表现差不多好,随机森林稍稍领先。这与前面从 f1_score 中得到的结果大为不同。因为平均准确率是从 0 到 1 的曲线下的面积,所以平均准确率总是返回一个在 0(最差)到 1(最好)之间的值。随机分配 decision_function 的分类器的平均准确率是数据集中正例样本所占的比例。
6)受试者工作特征(ROC)与AUC
还有一种常用的工具可以分析不同阈值的分类器行为:受试者工作特征曲线 (receiver operating characteristics curve),简称为 ROC 曲线 (ROC curve)。与准确率 - 召回率曲线类似,ROC 曲线考虑了给定分类器的所有可能的阈值,但它显示的是假正例率 (false positive rate,FPR)和真正例率 (true positive rate,TPR),而不是报告准确率和召回率。回想一下,真正例率只是召回率的另一个名称,而假正例率则是假正例占所有反类样本的比例:
![]()
可以用 roc_curve 函数来计算 ROC 曲线(见图 5-15):
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test, svc.decision_function(X_test))
plt.plot(fpr, tpr, label="ROC Curve")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
# 找到最接近于0的阈值
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-06.png', bbox_inches='tight')
plt.show()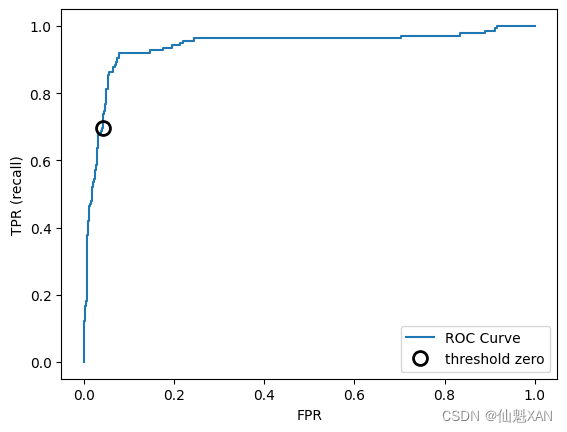
对于 ROC 曲线,理想的曲线要靠近左上角:你希望分类器的召回率很高,同时保持假正例率很低。从曲线中可以看出,与默认阈值 0 相比,我们可以得到明显更高的召回率(约 0.9),而 FPR 仅稍有增加。最接近左上角的点可能是比默认选择更好的工作点。同样请注意,不应该在测试集上选择阈值,而是应该在单独的验证集上选择。
图 5-16 给出了随机森林和 SVM 的 ROC 曲线对比:
from sklearn.metrics import roc_curve
fpr_rf, tpr_rf, thresholds_rf = roc_curve(y_test, rf.predict_proba(X_test)[:, 1])
plt.plot(fpr, tpr, label="ROC Curve SVC")
plt.plot(fpr_rf, tpr_rf, label="ROC Curve RF")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero SVC", fillstyle="none", c='k', mew=2)
close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5))
plt.plot(fpr_rf[close_default_rf], tpr[close_default_rf], '^', markersize=10,
label="threshold 0.5 RF", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-07.png', bbox_inches='tight')
plt.show()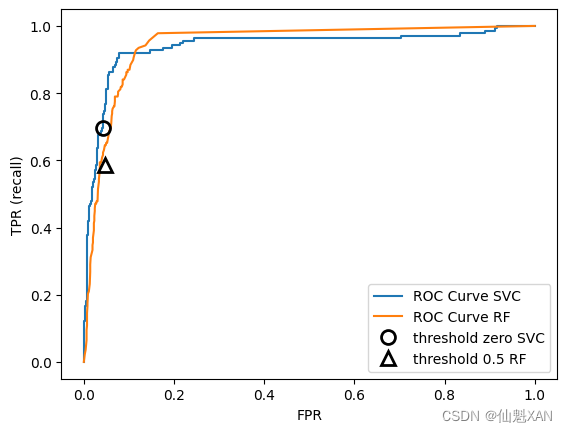
与准确率 - 召回率曲线一样,我们通常希望使用一个数字来总结 ROC 曲线,即曲线下的面积[通常被称为 AUC(area under the curve),这里的曲线指的就是 ROC 曲线]。我们可以利用 roc_auc_score 函数来计算 ROC 曲线下的面积:
from sklearn.metrics import roc_auc_score
rf_auc = roc_auc_score(y_test, rf.predict_proba(X_test)[:, 1])
svc_auc = roc_auc_score(y_test, svc.decision_function(X_test))
print("AUC for Random Forest: {:.3f}".format(rf_auc))
print("AUC for SVC: {:.3f}".format(svc_auc))AUC for Random Forest: 0.946 AUC for SVC: 0.940
利用 AUC 分数来比较随机森林和 SVM,我们发现随机森林的表现比 SVM 要略好一些。回想一下,由于平均准确率是从 0 到 1 的曲线下的面积,所以平均准确率总是返回一个 0(最差)到 1(最好)之间的值。随机预测得到的 AUC 总是等于 0.5,无论数据集中的类别多么不平衡。对于不平衡的分类问题来说,AUC 是一个比精度好得多的指标。AUC 可以被解释为评估正例样本的排名 (ranking)。它等价于从正类样本中随机挑选一个点,由分类器给出的分数比从反类样本中随机挑选一个点的分数更高的概率。因此,AUC 最高为 1,这说明所有正类点的分数高于所有反类点。对于不平衡类别的分类问题,使用 AUC 进行模型选择通常比使用精度更有意义。
我们回到前面研究过的例子:将 digits 数据集中的所有 9 与所有其他数据加以区分。我们将使用 SVM 对数据集进行分类,分别使用三种不同的内核宽度(gamma )设置(参见图 5-17):
y = digits.target == 9
X_train, X_test, y_train, y_test = train_test_split(
digits.data, y, random_state=0)
plt.figure()
for gamma in [1, 0.05, 0.01]:
svc = SVC(gamma=gamma).fit(X_train, y_train)
accuracy = svc.score(X_test, y_test)
auc = roc_auc_score(y_test, svc.decision_function(X_test))
fpr, tpr, _ = roc_curve(y_test , svc.decision_function(X_test))
print("gamma = {:.2f} accuracy = {:.2f} AUC = {:.2f}".format(
gamma, accuracy, auc))
plt.plot(fpr, tpr, label="gamma={:.3f}".format(gamma))
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.xlim(-0.01, 1)
plt.ylim(0, 1.02)
plt.legend(loc="best")
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-08.png', bbox_inches='tight')
plt.show()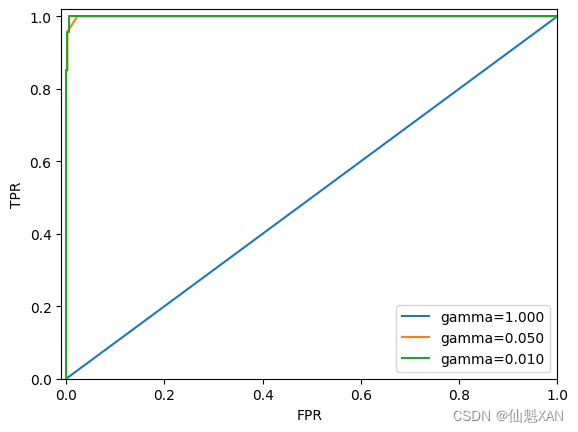
对于三种不同的 gamma 设置,其精度是相同的,都等于 90%。这可能与随机选择的性能相同,也可能不同。但是观察 AUC 以及对应的曲线,我们可以看到三个模型之间有明显的区别。对于 gamma=1.0 ,AUC 实际上处于随机水平,即 decision_function 的输出与随机结果一样好。对于 gamma=0.05 ,性能大幅提升至 AUC 等于 0.9。最后,对于 gamma=0.01 ,我们得到等于 1.0 的完美 AUC。这意味着根据决策函数,所有正类点的排名要高于所有反类点。换句话说,利用正确的阈值,这个模型可以对所有数据进行完美分类!10 知道这一点,我们可以调节这个模型的阈值并得到很好的预测结果。如果我们仅使用精度,那么将永远不会发现这一点。
因此,我们强烈建议在不平衡数据上评估模型时使用 AUC。但请记住,AUC 没有使用默认阈值,因此,为了从高 AUC 的模型中得到有用的分类结果,可能还需要调节决策阈值。
3、多分类指标
前面我们已经深入讨论了二分类任务的评估,下面来看一下对多分类问题的评估指标。多分类问题的所有指标基本上都来自于二分类指标,但是要对所有类别进行平均。多分类的精度被定义为正确分类的样本所占的比例。同样,如果类别是不平衡的,精度并不是很好的评估度量。想象一个三分类问题,其中 85% 的数据点属于类别 A,10% 属于类别 B,5% 属于类别 C。在这个数据集上 85% 的精度说明了什么?一般来说,多分类结果比二分类结果更加难以理解。除了精度,常用的工具有混淆矩阵和分类报告,我们在上一节二分类的例子中都见过。下面我们将这两种详细的评估方法应用于对 digits 数据集中 10 种不同的手写数字进行分类的任务:
from sklearn.metrics import accuracy_score
X_train, X_test, y_train, y_test = train_test_split(
digits.data, digits.target, random_state=0)
lr = LogisticRegression().fit(X_train, y_train)
pred = lr.predict(X_test)
print("Accuracy: {:.3f}".format(accuracy_score(y_test, pred)))
print("Confusion matrix:\n{}".format(confusion_matrix(y_test, pred)))Accuracy: 0.951 Confusion matrix: [[37 0 0 0 0 0 0 0 0 0] [ 0 40 0 0 0 0 0 0 2 1] [ 0 1 40 3 0 0 0 0 0 0] [ 0 0 0 43 0 0 0 0 1 1] [ 0 0 0 0 37 0 0 1 0 0] [ 0 0 0 0 0 46 0 0 0 2] [ 0 1 0 0 0 0 51 0 0 0] [ 0 0 0 1 1 0 0 46 0 0] [ 0 3 1 0 0 0 0 0 43 1] [ 0 0 0 0 0 1 0 0 1 45]]
模型的精度为 95.3%,这表示我们已经做得相当好了。混淆矩阵为我们提供了更多细节。与二分类的情况相同,每一行对应于真实标签,每一列对应于预测标签。图 5-18 给出了一张视觉上更加吸引人的图像:
# scores_image = mglearn.tools.heatmap(
# confusion_matrix(y_test, pred), xlabel='Predicted label',
# ylabel='True label', xticklabels=digits.target_names,
# yticklabels=digits.target_names, cmap=plt.cm.gray_r, fmt="%d")
def drawHeatmap(scores, xlabel,
ylabel='True label', fmt='{:0.2f}', colorbar=None):
# 反转scores数组的行顺序,以便(0, 0)在左下角
scores = scores[::-1, :]
# 绘制热图
fig, ax = plt.subplots()
if(colorbar is None):
colorbar = scores
cax = ax.matshow(colorbar, cmap='viridis')
fig.colorbar(cax)
# 假设param_grid['gamma']和param_grid['C']已经定义
# 这里我们使用字符串列表作为示例
param_grid = {
'gamma': ['0','1', '2', '3', '4', '5', '6', '7', '8', '9'],
'C': ['0','1', '2', '3', '4', '5', '6', '7', '8', '9']
}
# 设置xticks和yticks的位置
ticks_x = np.arange(len(param_grid['gamma']))
ticks_y = np.arange(len(param_grid['C']))[::-1] # 反转yticks的顺序以匹配反转的scores
# 设置xticklabels和yticklabels
ax.set_xticks(ticks_x)
ax.set_xticklabels(param_grid['gamma'])
ax.xaxis.set_tick_params(rotation=45)
ax.set_yticks(ticks_y)
ax.set_yticklabels(param_grid['C'])
# 设置x轴和y轴的标签
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
# 添加数值到每个单元格
for (i, j), z in np.ndenumerate(scores):
ax.text(j, i, fmt.format(z), ha='center', va='center')
drawHeatmap(confusion_matrix(y_test, pred), xlabel = 'Predicted label', ylabel='True label',fmt='{0}')
plt.title("Confusion matrix")
plt.gca().invert_yaxis()
# plt.tight_layout()
plt.savefig('Images/03EvaluationMetricsAndScoring-09.png', bbox_inches='tight')
plt.show()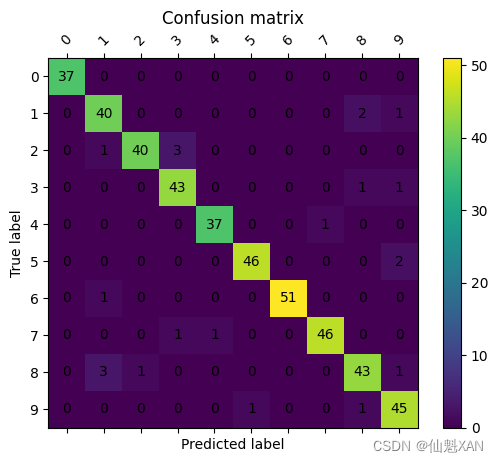
对于第一个类别(数字 0),它包含 37 个样本,所有这些样本都被划为类别 0(即类别 0 没有假反例)。我们之所以可以看出这一点,是因为混淆矩阵第一行中其他所有元素都为 0。我们还可以看到,没有其他数字被误分类为类别 0,这是因为混淆矩阵第一列中其他所有元素都为 0(即类别 0 没有假正例)。但是有些数字与其他数字混在一起——比如数字 2(第 3 行),其中有 3 个被划分到数字 3 中(第 4 列)。还有一个数字 3 被划分到数字 2 中(第 4 行第 3 列),一个数字 8 被划分到数字 2 中(第 9 行第 3 列)。
利用 classification_report 函数,我们可以计算每个类别的准确率、召回率和 f -分数:
print(classification_report(y_test, pred)) precision recall f1-score support
0 1.00 1.00 1.00 37
1 0.89 0.93 0.91 43
2 0.98 0.91 0.94 44
3 0.91 0.96 0.93 45
4 0.97 0.97 0.97 38
5 0.98 0.96 0.97 48
6 1.00 0.98 0.99 52
7 0.98 0.96 0.97 48
8 0.91 0.90 0.91 48
9 0.90 0.96 0.93 47
accuracy 0.95 450
macro avg 0.95 0.95 0.95 450
weighted avg 0.95 0.95 0.95 450
不出所料,类别 0 的准确率和召回率都是完美的 1,因为这个类别中没有混淆。另一方面,对于类别 7,准确率为 1,这是因为没有其他类别被误分类为 7;而类别 6 没有假反例,所以召回率等于 1。我们还可以看到,模型对类别 8 和类别 3 的表现特别不好。
对于多分类问题中的不平衡数据集,最常用的指标就是多分类版本的 f -分数。多分类 f -分数背后的想法是,对每个类别计算一个二分类 f -分数,其中该类别是正类,其他所有类别组成反类。然后,使用以下策略之一对这些按类别 f -分数进行平均。
- “宏”(macro)平均:计算未加权的按类别 f -分数。它对所有类别给出相同的权重,无论类别中的样本量大小。
- “加权”(weighted)平均:以每个类别的支持作为权重来计算按类别 f -分数的平均值。分类报告中给出的就是这个值。
- “微”(micro)平均:计算所有类别中假正例、假反例和真正例的总数,然后利用这些计数来计算准确率、召回率和 f -分数。
如果你对每个样本 等同看待,那么推荐使用“微”平均 f 1 -分数;如果你对每个类别 等同看待,那么推荐使用“宏”平均 f 1 -分数:
print("Micro average f1 score: {:.3f}".format
(f1_score(y_test, pred, average="micro")))
print("Macro average f1 score: {:.3f}".format
(f1_score(y_test, pred, average="macro")))Micro average f1 score: 0.951 Macro average f1 score: 0.952
4、回归指标
对回归问题可以像分类问题一样进行详细评估,例如,对目标值估计过高与目标值估计过低进行对比分析。但是,对于我们见过的大多数应用来说,使用默认 R2 就足够了,它由所有回归器的 score 方法给出。业务决策有时是根据均方误差或平均绝对误差做出的,这可能会鼓励人们使用这些指标来调节模型。但是一般来说,我们认为 R2 是评估回归模型的更直观的指标。
5、在模型选择中使用评估指标
前面详细讨论了许多种评估方法,以及如何根据真实情况和具体模型来应用这些方法。但我们通常希望,在使用 GridSearchCV 或 cross_val_score 进行模型选择时能够使用 AUC 等指标。幸运的是,scikit-learn 提供了一种非常简单的实现方法,就是 scoring 参数,它可以同时用于 GridSearchCV 和 cross_val_score 。你只需提供一个字符串,用于描述想要使用的评估指标。举个例子,我们想用 AUC 分数对 digits 数据集中“9 与其他”任务上的 SVM 分类器进行评估。想要将分数从默认值(精度)修改为 AUC,可以提供 "roc_auc" 作为 scoring 参数的值:
from sklearn.model_selection import cross_val_score
# 分类问题的默认评分是精度
print("Default scoring: {}".format(
cross_val_score(SVC(), digits.data, digits.target == 9)))
# 指定"scoring="accuracy"不会改变结果
explicit_accuracy = cross_val_score(SVC(), digits.data, digits.target == 9,
scoring="accuracy")
print("Explicit accuracy scoring: {}".format(explicit_accuracy))
roc_auc = cross_val_score(SVC(), digits.data, digits.target == 9,
scoring="roc_auc")
print("AUC scoring: {}".format(roc_auc))
Default scoring: [0.975 0.99166667 1. 0.99442897 0.98050139] Explicit accuracy scoring: [0.975 0.99166667 1. 0.99442897 0.98050139] AUC scoring: [0.99717078 0.99854252 1. 0.999828 0.98400413]
类似地,我们可以改变 GridSearchCV 中用于选择最佳参数的指标:
from sklearn.model_selection import GridSearchCV
X_train, X_test, y_train, y_test = train_test_split(
digits.data, digits.target == 9, random_state=0)
# 我们给出了不太好的网格来说明:
param_grid = {'gamma': [0.0001, 0.01, 0.1, 1, 10]}
# 使用默认的精度:
grid = GridSearchCV(SVC(), param_grid=param_grid)
grid.fit(X_train, y_train)
print("Grid-Search with accuracy")
print("Best parameters:", grid.best_params_)
print("Best cross-validation score (accuracy)): {:.3f}".format(grid.best_score_))
print("Test set AUC: {:.3f}".format(
roc_auc_score(y_test, grid.decision_function(X_test))))
print("Test set accuracy: {:.3f}".format(grid.score(X_test, y_test)))Grid-Search with accuracy
Best parameters: {'gamma': 0.0001}
Best cross-validation score (accuracy)): 0.976
Test set AUC: 0.992
Test set accuracy: 0.973
# 使用AUC评分来代替:
grid = GridSearchCV(SVC(), param_grid=param_grid, scoring="roc_auc")
grid.fit(X_train, y_train)
print("\nGrid-Search with AUC")
print("Best parameters:", grid.best_params_)
print("Best cross-validation score (AUC): {:.3f}".format(grid.best_score_))
print("Test set AUC: {:.3f}".format(
roc_auc_score(y_test, grid.decision_function(X_test))))
print("Test set accuracy: {:.3f}".format(grid.score(X_test, y_test)))Grid-Search with AUC
Best parameters: {'gamma': 0.01}
Best cross-validation score (AUC): 0.998
Test set AUC: 1.000
Test set accuracy: 1.000
在使用精度时,选择的参数是 gamma=0.0001 ,而使用 AUC 时选择的参数是 gamma=0.01 。在两种情况下,交叉验证精度与测试集精度是一致的。但是,使用 AUC 找到的参数设置,对应的 AUC 更高,甚至对应的精度也更高( 利用 AUC 找到了精度更高的模型,这可能是因为对于不平衡数据来说,精度并不是模型性能的良好度量)。
对于分类问题,scoring 参数最重要的取值包括:accuracy (默认值)、roc_auc (ROC 曲线下方的面积)、average_precision (准确率 - 召回率曲线下方的面积)、f1 、f1_macro 、f1_micro 和 f1_weighted (这四个是二分类的 f 1 -分数以及各种加权变体)。对于回归问题,最常用的取值包括:r2 ( 分数)、
mean_squared_error (均方误差)和 mean_absolute_error (平均绝对误差)。你可以在文档中找到所支持参数的完整列表(3.4. Metrics and scoring: quantifying the quality of predictions — scikit-learn 1.5.0 documentation ),也可以查看 metrics.scorer 模块中定义的 SCORER 字典。
from sklearn.metrics import get_scorer_names
# 打印可用的评分器
print("Available scorers:\n{}".format(sorted(get_scorer_names())))Available scorers: ['accuracy', 'adjusted_mutual_info_score', 'adjusted_rand_score', 'average_precision', 'balanced_accuracy', 'completeness_score', 'd2_absolute_error_score', 'explained_variance', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'fowlkes_mallows_score', 'homogeneity_score', 'jaccard', 'jaccard_macro', 'jaccard_micro', 'jaccard_samples', 'jaccard_weighted', 'matthews_corrcoef', 'max_error', 'mutual_info_score', 'neg_brier_score', 'neg_log_loss', 'neg_mean_absolute_error', 'neg_mean_absolute_percentage_error', 'neg_mean_gamma_deviance', 'neg_mean_poisson_deviance', 'neg_mean_squared_error', 'neg_mean_squared_log_error', 'neg_median_absolute_error', 'neg_negative_likelihood_ratio', 'neg_root_mean_squared_error', 'neg_root_mean_squared_log_error', 'normalized_mutual_info_score', 'positive_likelihood_ratio', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'rand_score', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc', 'roc_auc_ovo', 'roc_auc_ovo_weighted', 'roc_auc_ovr', 'roc_auc_ovr_weighted', 'top_k_accuracy', 'v_measure_score']
附录
一、参考文献
参考文献:[德] Andreas C. Müller [美] Sarah Guido 《Python Machine Learning Basics Tutorial》