✨题目链接:
dd爱旋转
✨题目描述
读入一个n∗n的矩阵,对于一个矩阵有以下两种操作
1:顺时针旋180°
2:关于行镜像
如
变成
给出q个操作,输出操作完的矩阵
✨输入描述:
第一行一个数n(1≤n≤1000),表示矩阵大小
接下来n行,每行n个数,描述矩阵,其中数字范围为[1,2000]
一下来一行一个数q(1≤q≤100000),表示询问次数
接下来q行,每行一个数x(x=1或x=2),描述每次询问
✨输出描述:
n行,每行n个数,描述操作后的矩阵
✨示例1
📍输入
2
1 2
3 4
1
1
📍输出
4 3
2 1
✨示例2
📍输入
2
1 2
3 4
1
2
📍输出
3 4
1 2
✨解题思路
- 我们先分析两种操作
- 顺时针旋180°
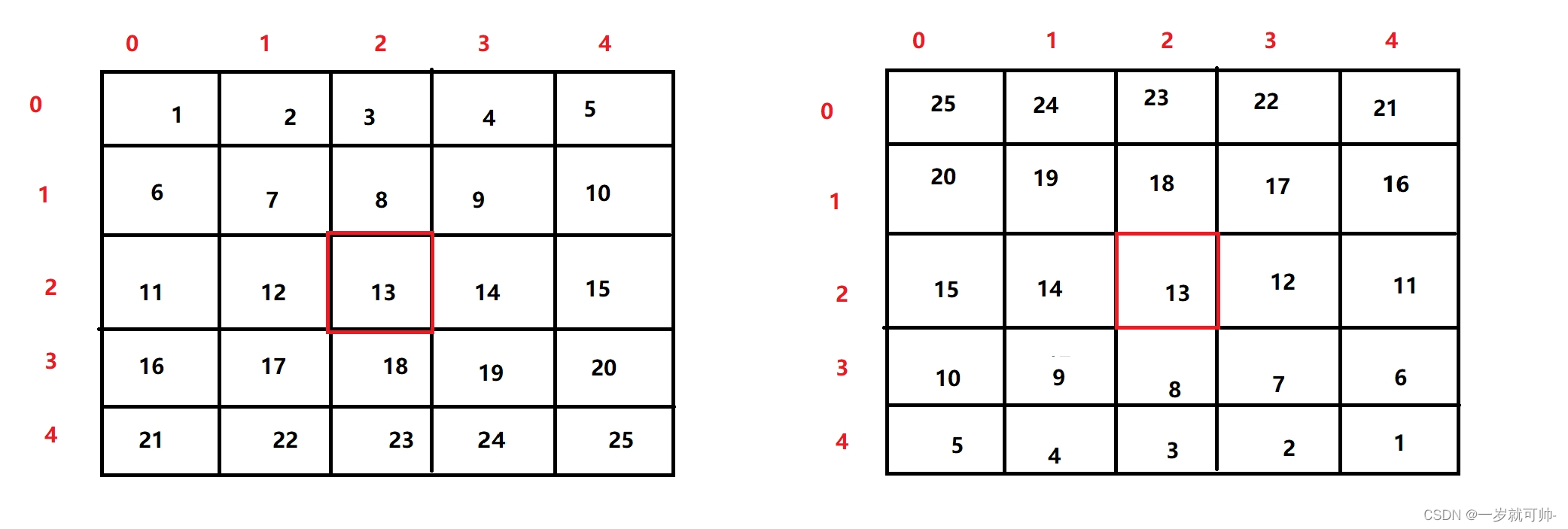 我们发现选转一次只需要从i=0向后遍历到
我们发现选转一次只需要从i=0向后遍历到位置每次交换矩阵的[x][y]与[n-1-x][n-1-y]的值就可以实现一次旋转,从 i 到
当前行可以用 i/n 得到 当前列可以用 i%n 得到。
- 关于行镜像
 我们遍历行的一半,每次与n-i行交换一整行即可得到行镜像
我们遍历行的一半,每次与n-i行交换一整行即可得到行镜像
- 我们发现两种操作,如果连续操作 两次矩阵会恢复为原来的样子
- 所以先整理输入的操作数数据
- 通过栈来把连续的两个操作数进行消除
- 遍历栈的元素进行两种操作
- 最后打印矩阵
✨代码
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
void operate1(vector<vector<int>>& v) {
int n = v.size();
for (int i = 0; i < n * n / 2; i++) {
//行 i/v.size() 列 i%v.size()
int x = i / v.size();
int y = i % v.size();
int tmp = v[x][y];
v[x][y] = v[n - 1 - x][n - 1 - y];
v[n - 1 - x][n - 1 - y] = tmp;
}
}
void operate2(vector<vector<int>>& v) {
int x = v.size();
for (int i = 0; i < x / 2; i++) {
v[i].swap(v[x - i - 1]);
}
}
int main() {
int n;
cin >> n;
vector<vector<int>> v(n, vector<int>(n));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> v[i][j];
}
}
int q, tmp;
stack<int> st;
cin >> q;
while (q--) {
cin >> tmp;
if (!st.empty()) {
if (tmp == st.top()) {
st.pop();
} else {
st.push(tmp);
}
} else {
st.push(tmp);
}
}
while (!st.empty()) {
if (st.top() == 1)operate1(v);
else operate2(v);
st.pop();
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << v[i][j] << " ";
}
cout << endl;
}
return 0;
}
※ 如果文章对你有帮助的话,可以点赞收藏!!谢谢支持








![[数据集][目标检测]航空发动机缺陷检测数据集VOC+YOLO格式291张4类别](https://img-blog.csdnimg.cn/direct/5ed54f22273c45f1b5861df81b7e9c7c.png)