gitee代码获取链接：https://gitee.com/flying-wolf-loves-learning/data-structure.git

一、树的概念

1.1 概念简述

数据结构中的树是一种层次结构，它由节点（node）和边（edge）组成。每个节点都有零个或多个子节点，一个节点被称为另一个节点的父节点（parent node）如果它是该节点的直接上一级，而该节点被称为父节点的子节点（child node）。

树结构中有一个特殊的节点称为根节点（root node），它位于树的顶部，并且没有父节点。根节点之外的所有其他节点都有一个唯一的父节点。树中没有子节点的节点称为叶节点（leaf node），也称为终端节点（terminal node）。叶节点是树结构中的末端节点，它们没有任何子节点。

树结构可以是有向的或无向的。在有向树中，节点之间的关系是单向的，即每个节点只有一个父节点，而在无向树中，节点之间的关系是双向的，没有明确的父节点子节点之分。

树（Tree）是n（n≥0）个节点的有限集合T，它满足两个条件 ：
有且仅有一个特定的称为根（Root）的节点；
其余的节点可以分为m（m≥0）个互不相交的有限集合T1、T2、……、Tm，其中每一个集合又是一棵树，并称为其根的子树。

表示方法 ：树形表示法、目录表示法。

1.2 基本术语

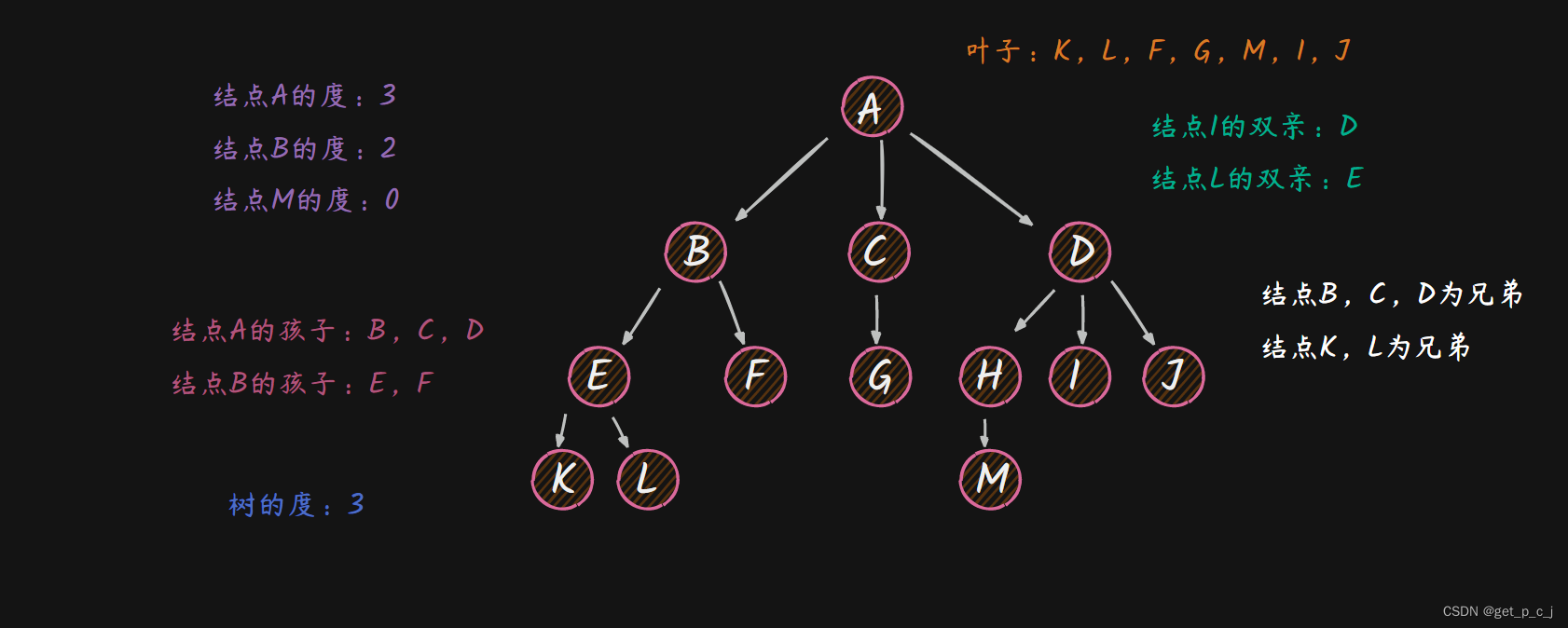
一个节点的子树的个数称为该节点的度数。
一棵树的度数是指该树中节点的最大度数。
度数为零的节点称为树叶或终端节点。
度数不为零的节点称为分支节点。
除根节点外的分支节点称为内部节点。

一个节点系列k1,k2, ……,ki,ki+1, ……,kj,并满足ki是ki+1的父节点，就称为一条从k1到kj的路径。
路径的长度为j-1,即路径中的边数。
路径中前面的节点是后面节点的祖先，后面节点是前面节点的子孙。
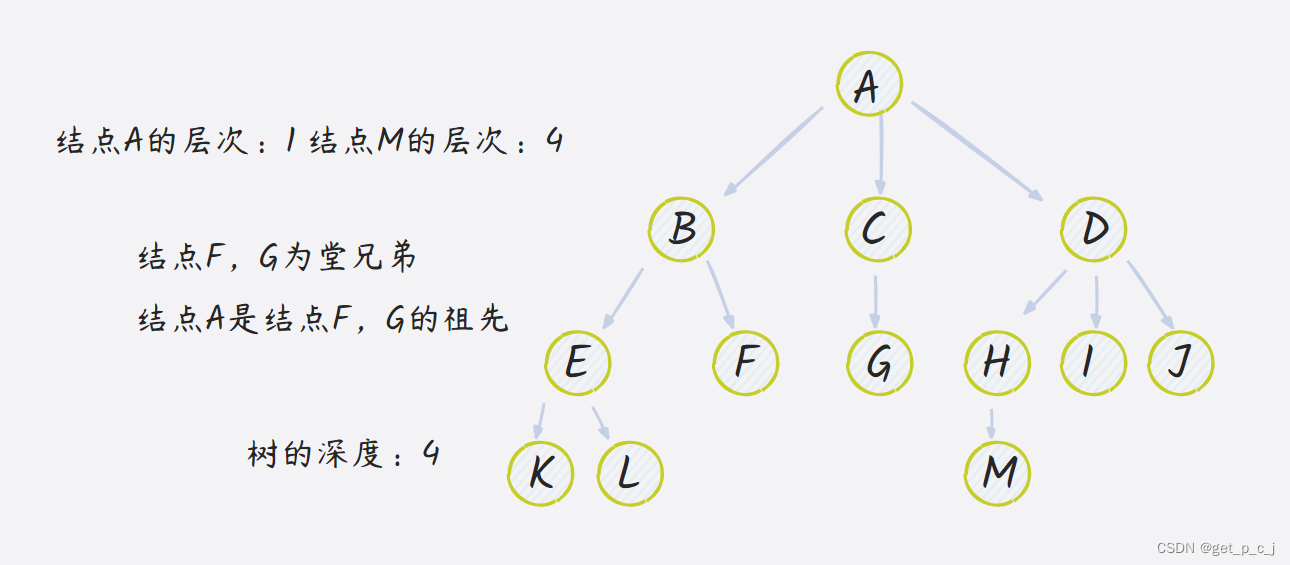
节点的层数等于父节点的层数加一，根节点的层数定义为一。树中节点层数的最大值称为该树的高度或深度。

• 若树中每个节点的各个子树的排列为从左到右，不能交换，即兄弟之间是有序的，则该树称为有序树。
• m（m≥0）棵互不相交的树的集合称为森林。
• 树去掉根节点就成为森林，森林加上一个新的根节点就成为树。
• 树的逻辑结构 ：树中任何节点都可以有零个或多个直接后继节点（子节点），但至多只有一个直接前趋节点（父节点），根节点没有前趋节点，叶节点没有后继节点。

1.3 树的应用

树结构在计算机科学中有广泛的应用，例如在操作系统中的文件系统，数据库中的索引结构，网络中的路由算法等等。树结构的灵活性和高效性使其成为解决许多问题的理想选择。

二、二叉树的原理

2.1 二叉树

• 二叉树是n（n≥0）个节点的有限集合或者是空集（n＝0）
• 或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。
• 严格区分左子树和右子树，即使只有一个子节点也要区分左右。

2.2 性质

• 二叉树第i（i≥1）层上的节点最多为2i-1个。
深度为k（k≥1）的二叉树最多有2k－1个节点。

• 满二叉树 ：深度为k（k≥1）时有2k－1个节点的二叉树。

• 完全二叉树 ：只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上。具有n个节点的完全二叉树的深度为
（log2n）＋1或『log2(n+1)。

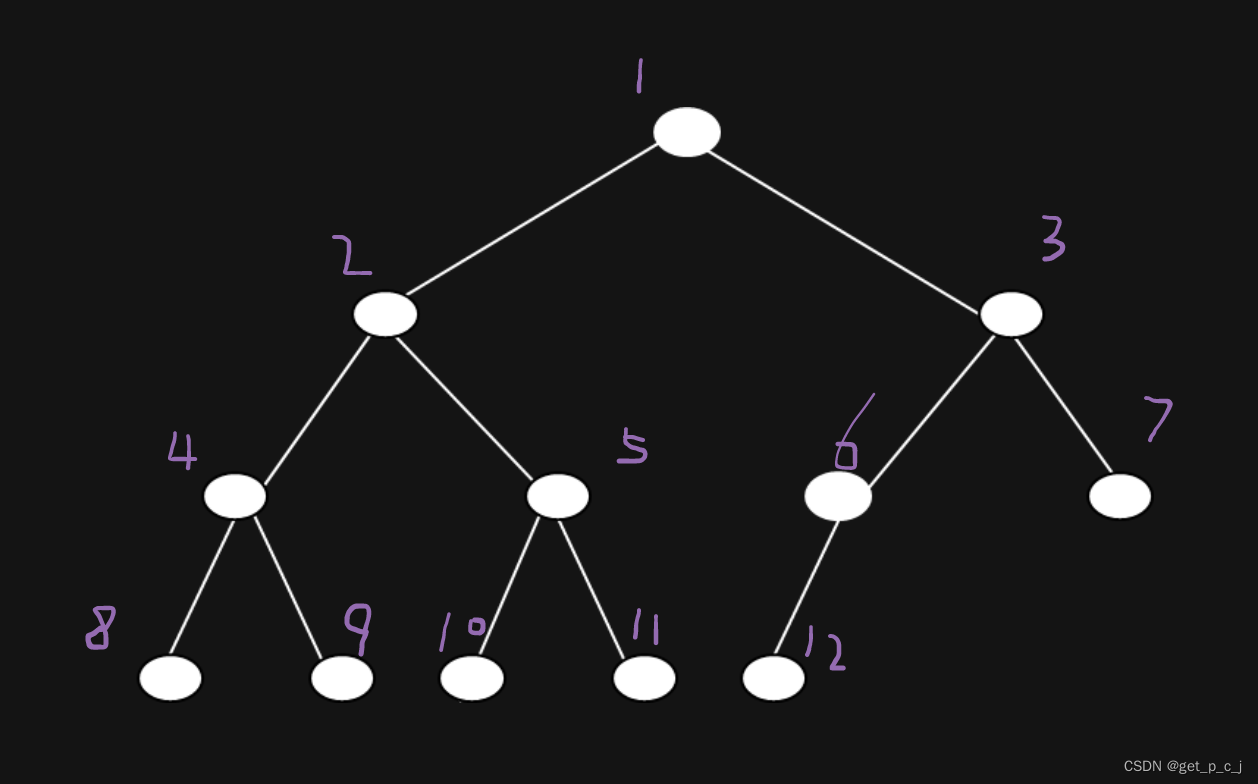
•顺序存储结构 ：完全二叉树节点的编号方法是从上到下，从左到右，根节点为1号节点。设完全二叉树的节点数为n，某节点编号为i
当i＞1（不是根节点）时，有父节点，其编号为i/2;
当2i≤n时，有左孩子，其编号为2i ,否则没有左孩子，本身是叶节点;
当2i＋1≤n时，有右孩子，其编号为2i+1 ,否则没有右孩子；
当i为奇数且不为1时，有左兄弟，其编号为i-1,否则没有左兄弟；
当i为偶数且小于n时，有右兄弟，其编号为i＋1,否则没有右兄弟；

有n个节点的完全二叉树可以用有n+1个元素的数组进行顺序存储，节点号和数组下标一一对应，下标为零的元素不用。
利用以上特性，可以从下标获得节点的逻辑关系。不完全二叉树通过添加虚节点构成完全二叉树，然后用数组存储，这要浪费一些存储空间。

链式存储结构是实现二叉树的一种常见方式，它通过链表结构来表示节点之间的关系。在链式存储的二叉树中，每个节点是一个结构体或类，包含三个部分：节点值、指向左子节点的指针和指向右子节点的指针。

typedef int data_t ;		
typedef struct node_t;		
{
	data_t data ; 		
	struct node_t *lchild , *rchild ; 	
} bitree_t ; 	
		
bitree_t *root ; 	 
二叉树由根节点指针决定。

三、二叉树的运算

遍历 ：沿某条搜索路径周游二叉树，对树中的每一个节点访问一次且仅访问一次。

二叉树是非线性结构，每个结点有两个后继，则存在如何遍历即按什么样的搜索路径进行遍历的问题。

由于二叉树的递归性质，遍历算法也是递归的。三种基本的遍历算法如下 ：
先序：先访问树根，再访问左子树，最后访问右子树；
中序：先访问左子树，再访问树根，最后访问右子树；
后序：先访问左子树，再访问右子树，最后访问树根；

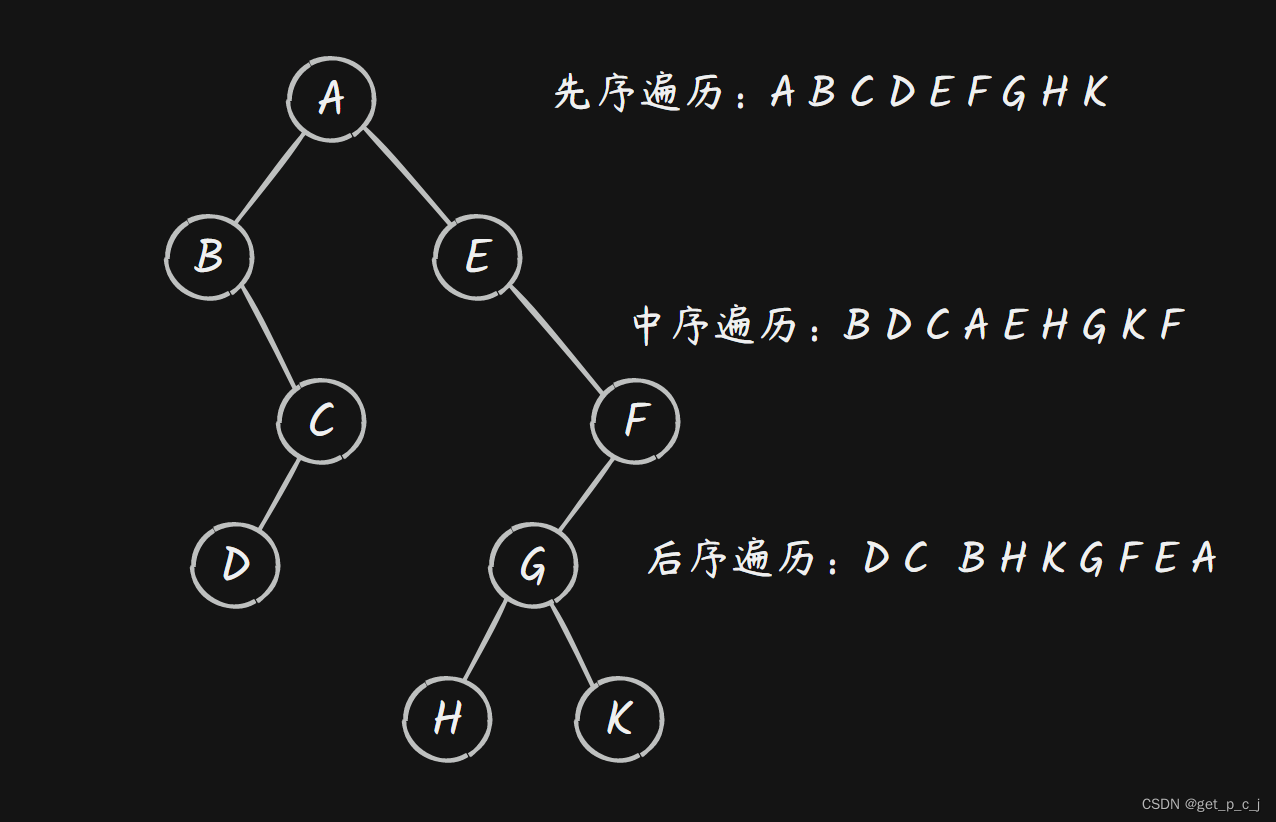
四、二叉树的三种遍历

4.1 树的创建

bitree *tree_create(){
    data_t ch; // 用于存储输入的字符
    bitree *r; // 指向当前节点的指针

    scanf("%c", &ch); // 从标准输入读取一个字符存储到变量 ch 中
    if(ch == '#'){ // 如果当前字符是 '#'，表示空节点，直接返回 NULL
        return NULL;
    }

    if((r = (bitree *)malloc(sizeof(bitree))) == NULL){ // 分配内存给新节点，并进行错误检查
        printf("malloc failed\n"); // 输出错误信息
        return NULL; // 返回 NULL 表示内存分配失败
    }
    r->data = ch; // 将当前字符存储到新节点的数据域中

    // 递归调用 tree_create() 函数创建当前节点的左子树，并将返回的根节点指针赋给当前节点的左孩子指针
    r->left = tree_create();
    // 递归调用 tree_create() 函数创建当前节点的右子树，并将返回的根节点指针赋给当前节点的右孩子指针
    r->right = tree_create();

    return r; // 返回当前节点指针，即指向根节点的指针
}

这段代码实现了一个递归创建二叉树的函数 tree_create()。通过不断地从标准输入读取字符，并根据字符的内容来构建二叉树的节点，实现了根据输入创建二叉树的功能。

4.2 先序遍历算法

若二叉树为空树，则空操作；否则
访问根结点
先序遍历左子树
先序遍历右子树

void preorder(bitree *r){
    // 如果当前节点为空，直接返回，结束递归
    if(NULL == r){
        return;
    }

    // 输出当前节点的数据域值，即当前节点的字符
    printf("%c", r->data);

    // 递归调用 preorder() 函数遍历当前节点的左子树
    preorder(r->left);
    // 递归调用 preorder() 函数遍历当前节点的右子树
    preorder(r->right);
}

这段代码实现了二叉树的前序遍历算法。前序遍历的过程是先访问根节点，然后递归地遍历左子树，最后递归地遍历右子树。在遍历过程中，每个节点的数据域值（即存储的字符）都会被输出。

4.3 中序遍历算法

若二叉树为空树，则空操作；否则
先序遍历左子树
访问根结点
先序遍历右子树

void inorder(bitree *r){
    // 如果当前节点为空，直接返回，结束递归
    if(NULL == r){
        return;
    }

    // 递归调用 inorder() 函数遍历当前节点的左子树
    inorder(r->left);
    
    // 输出当前节点的数据域值，即当前节点的字符
    printf("%c", r->data);
    
    // 递归调用 inorder() 函数遍历当前节点的右子树
    inorder(r->right);
}

这段代码实现了二叉树的中序遍历算法。中序遍历的过程是先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。在遍历过程中，每个节点的数据域值（即存储的字符）都会被输出。

4.4 后序遍历算法

若二叉树为空树，则空操作；否则
先序遍历左子树
先序遍历右子树
访问根结点

void posorder(bitree *r){
    // 如果当前节点为空，直接返回，结束递归
    if(NULL == r){
        return;
    }

    // 递归调用 posorder() 函数遍历当前节点的左子树
    posorder(r->left);
    
    // 递归调用 posorder() 函数遍历当前节点的右子树
    posorder(r->right);
    
    // 输出当前节点的数据域值，即当前节点的字符
    printf("%c", r->data);
}

这段代码实现了二叉树的后序遍历算法。后序遍历的过程是先递归地遍历左子树，然后递归地遍历右子树，最后访问根节点。在遍历过程中，每个节点的数据域值（即存储的字符）都会被输出。

五、二叉树的参次遍历

5.1 层次遍历

由于层次遍历（也称为广度优先遍历）是按照树的层次从上到下、从左到右的顺序遍历节点，我们通常需要借助队列来辅助实现。不过，从给定的前序遍历和中序遍历结果中，我们不能直接得出层次遍历的结果，因为层次遍历并不直接反映树的父子关系，而是反映了节点在树中的层次位置。

但我们可以根据前序遍历和中序遍历的结果先构造出二叉树，然后再进行层次遍历。

void layerorder(bitree *r){
    linkqueue *lq;

    // 创建一个链式队列，用于层序遍历
    if((lq = queue_create()) == NULL){
        return;
    }
    
    // 如果根节点为空，则直接返回
    if(r == NULL){
        return;
    }
    
    // 输出根节点的数据域值，即根节点的字符
    printf("%c", r->data);
    
    // 将根节点入队
    enqueue(lq, r);

    // 遍历队列中的元素，直到队列为空
    while(!queue_empty(lq)){
        // 出队一个节点
        r = dequeue(lq);
        
        // 如果当前节点有左孩子，则输出左孩子的数据域值，并将左孩子入队
        if(r->left){
            printf("%c", r->left->data);
            enqueue(lq, r->left);
        }
        
        // 如果当前节点有右孩子，则输出右孩子的数据域值，并将右孩子入队
        if(r->right){
            printf("%c", r->right->data);
            enqueue(lq, r->right);
        }
    }
    // 输出换行符，表示层序遍历结束
    puts("");
}

这段代码实现了二叉树的层序遍历算法。层序遍历是从上到下、从左到右逐层访问每个节点，先访问根节点，然后依次访问每一层的节点。在遍历过程中，每个节点的数据域值（即存储的字符）都会被输出。

5.2 牛刀小试

已知遍历结果如下，试画出对应的二叉树
前序： A B C E H F I J D G K
中序： A H E C I F J B D K G
（利用遍历规则的特点，还原二叉树，提交还原的二叉树，或者写出后序遍历结果）

5.3 问题解答

由前序遍历的特点可知A是根节点，结合中序遍历可知A没有左子树，则B为A的右子树。
将B视为根则从中序遍历中观察到AHECIFJ都是在B的左分支后代，DKG则处于B的右分支后代，利用先序特点可知C为B的左子树，利用后序遍历的特点可知D为B的右子树。这样推理下去就能得到具体的二叉树图。

二叉树图如下：

由此可以写出后序遍历的结果：HEIJFCKGDBA