快速排序算法备考

news2025/2/25 17:18:59

快排模板

快速排序(快排) (C语言实现)_c语言快速排序_Brant_zero2022的博客-CSDN博客
快排使用递归来实现
关键思想:划分


//划分
int partion(int A[],int L,int R){
      int mid=A[L];
	while(L<R){
	//每一次划分:左边元素<枢轴元素<右边元素
	//R往前找，直到找到一个比mid小的元素，然后把A[R]放在A[L]的位置
       while(A[R]>=mid && L<R){
           R--;
       }
        A[L]=A[R];
		while(A[R]<=mid && L<R){
           L++;
       }
    	A[R]=A[L];
    }
    //存放枢轴元素
     A[L]=mid;
    return L；
}

//快排
void quickSort(int A[],int L,int R){
	if(L>=R) return;//递归终止
    int M=partion(A,L,R);//返回中轴元素的下标
    //对中轴元素两边分别排序
    quickSort(A,L,M-1);
    quickSort(A,M+1,R);

}

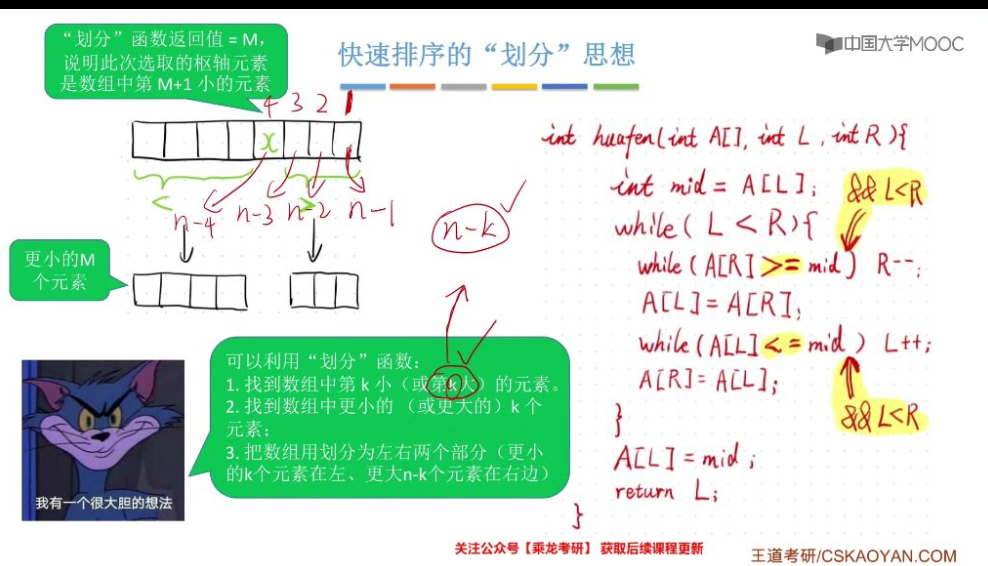
快排的划分思想

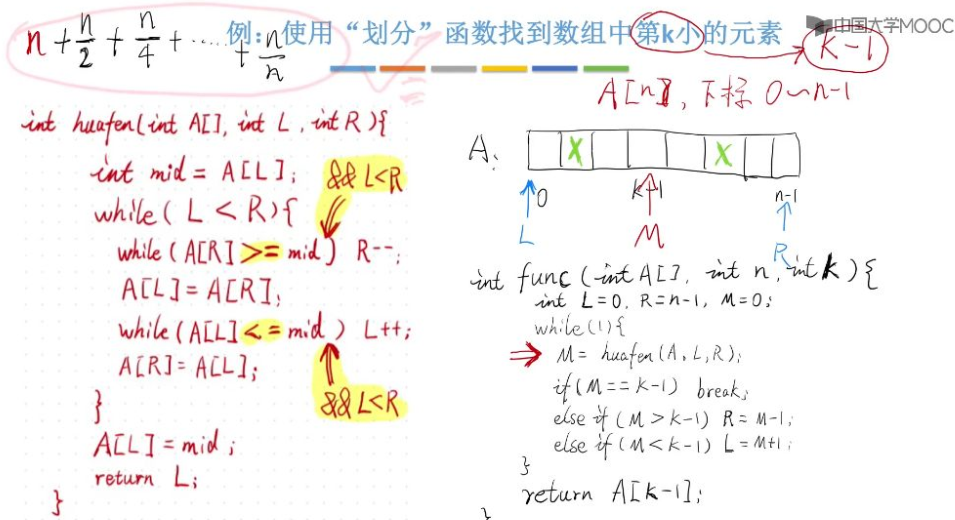
快排划分思想的算法题

使用划分函数找到数组中第k小的元素

数组中第k小的元素，说明这个元素的左边有k-1个元素比它小，利用快排的划分思想，我们只需要让划分函数返回k-1，就可以找到第k小元素。
如果第一次划分后，返回下标为k-1，那么，我们就找到了这个元素
如果返回的下标>k-1,说明接下来要在[L,M-1]进行划分
如果返回的下标<k-1,说明接下来要在右边进行划分


int partion(int A[],int L,int R){
	int mid=A[L];
	while(L<R){	
        while(A[R]>=mid && L<R) R--;
        A[L]=A[R];
        while(A[L]<=mid && L<R) L++
            A[R]=A[L];
    }
    A[L]=mid;

}
//非递归实现
int min_k(int A[],int n,int k){
    int L=0,R=n-1;
	int M=0;
    while(1){
    M=partion(A,L,R);
 	if(M==k-1)  break;//说明找到了
    else if(M<k-1){
    	//在右边进行划分
       L=M+1;
    }else{
        //在左边进行划分
    	R=M-1;
    }

    }
   
	return A[K-1]

}

//递归实现
int min_k(int A[],int L,int R){
	int M=partion(A,L,R);
    if(M==k-1)  return A[M];//说明找到了
    else if(M<k-1){
    	//在右边进行划分
        min_k(A,M+1,R);
    }else{
    	min_k(A,L,M-1);

    }


}

分析非递归的复杂度

王道课后习题:在数组中找到第k小的元素

第k小，说明左边有k-1个元素比它小，利用快排的划分思想，只要返回下标为k即可

利用划分思想
//返回划分后的中轴元素的下标
int partion(int L,int left,int right){
	int mid=L[left];
    while(left<right){
    	while(L[right]>=mid && left<right) right--;
        L[left]=L[right];
        while(L[left]<=mid && left<=right) left++;
        L[right]=L[left];
    }
    L[left]=mid;
	return left;

}

int min_k(int L[],int n,int k){
    int left=1,right=n,M=0;
    while(1){
	  M=partion(L,left,right);
      if(M==k) break;
        else if(M<k)  left=M+1;//要在右边进行划分
    	else right=M-1;//左边划分
    }
	return L[k];



}

快排算法题实战应用

2011年42题

方法一双指针(我自己第一遍就想到的思路）

使用双指针，i指向序列S1元素，j指向S2序列元素,cnt用来记录已经比较的次数。比较s1,s2所指元素大小，如果S1所指元素大，则j向后移动，然后cnt++,如果S2所指元素大，则i向后移动，cnt++,当cnt==L/2时，此时，s1,s2所指元素大的那个就是中位数
代码


int find(int s1[],int s2[],int n){
	int i=j=cnt=0;
    for(cnt=0;cnt<n/2;cnt++;){
    	if(s1[i]<s2[j]){
            i++;
        }
        else{
           j++; 
        } 
    }
    //接下来比较s1,s2所指元素大小
    if(s1[i]>s2[j]){
        return s1[i];
    }else{
        return s2[j];
    }


}

时间复杂度:o(n)
空间复杂度:o(1)

方法二利用快排解决问题

把两个数组合并成一个大数组，然后用快排，下标L/2的元素就是中位数


//快排划分
int partion(int a[].int L,int R){
	int mid=a[L];
	while(L<R){
   	 while(a[R]>=mid&& L<R) R--;
    	a[L]=a[R];
    while(a[L]>=mid && L<R) L++;
        a[R]=a[L];
        a[L]=mid;
        return L;


}
//快排
    void qSort(int a[],int L,int R){
    	if(L<=R) return;
        int M=partion(a,L,R);
        qSort(a,L,M-1);
        qSort(a,M+1,R);
    }

    void find(int s1[],int s2[],int n){
    	int a[2*n];
        int i,j=0;
        //合并成一个数组
        for( i=0;i<n;i++)
            c[j++]=s1[i];
        }
    	for( i=n;i<2*n;j++){
    		c[j++]=s2[i];
    	}
    //排序
    qSort(a,0,2*n-1);
    return (0+2*n-1)/2;



    }

2013年41题

方法一利用哈希表(第一遍所想)

1.cnt数组记录元素大小0~n-1出现的次数，出现次数大于n/2的元素就是主元素
2.代码

void mainElement(int a[],int n){
	int cnt[n]={0};
    //元素值为i就存放在cnt数组的下标为i的位置，并且cnt对应位置元素值+1
    for(int i=0;i<n;i++){
    	cnt[a[i]]++;
    }
	//扫描cnt数组
    for(int i=0;i<n;i++){
    	if(cnt[i]>n/2) court<<i<<endl;
    }
    court<<"不存在主元素"<<endl;

}
3.时间复杂度:o(n)
    空间复杂度o(n)

方法二快排

主元素的元素数量超过数组长度的一半，如果数组有序，并且存在主元素，那么主元素一定在数组的中间位置

①无序--->有序  快排
②找n/2位置的元素
③从n/2往左、往右统计个数，然后判断存不存在

2018年41题

方法一哈希表

cnt数组用来记录元素i是否出现在数组中，cnt记录1_{n，如果元素i位于1}n，则对应cnt数组相应位置+1


int fun(int a[],int n){
	int cnt[n+1];
    for(int i=0;i<n;i++){
        if(a[i]>=1 && a[i]<=n) {
        	cnt[a[i]]++;
        }
    }

//遍历cnt数组，如果cnt[i]==0，说明就是未出现的最小正整数
    for(int i=1;i<n;i++){
    	if(cnt[i]==0) return i;

    }
    //说明1~n都存在
    return n+1;

    
}

时间复杂度  O(n)
    空间复杂度  O(n)

方法二快排

2016年43题(本质是把乱序数组排成有序)

方法一利用快排

思路:想办法让右边元素大，左边元素小，而且尽量要把数组尽量平分，想到快排的划分思想，为了满足上述条件，右半部分的元素不能比左边元素个数少。
左边:0~n/2-1
右边:n/2~n-1

把数组A排成递增有序数列，排序后集合A1为[0,n/2-1],集合A2为[n/2n-1]

此时[S1-S2]最大，[n1-n2]最小
2.代码

①无序数组拍成有序数组
②说明A1,A2所在区间范围

 
//划分
int partion(int A[],int L,int R){
      int mid=A[L];
	while(L<R){
	//每一次划分:左边元素<枢轴元素<右边元素
	//R往前找，直到找到一个比mid小的元素，然后把A[R]放在A[L]的位置
       while(A[R]>=mid && L<R){
           R--;
       }
        A[L]=A[R];
		while(A[R]<=mid && L<R){
           L++;
       }
    	A[R]=A[L];
    }
    //存放枢轴元素
     A[L]=mid;
    return L；
}





//快排
void quickSort(int A[],int L,int R){
	if(L>=R) return;//递归终止
    int M=partion(A,0,n-1);//返回中轴元素的下标
    //对中轴元素两边分别排序
    quickSort(A,L,M-1);
    quickSort(A,M+1,R);

}

时间复杂度

空间复杂度

方法二利用划分的思想(最优解)

我们知道快排在进行一次划分后，该元素的左边元素都比它小，右边都比它大。我们这道题目本质是把元素大的放右边，元素小的放左边，并没有要求按照递增进行排序。其实，我们只要找到数组中第n/2小的元素。只要这个元素的位置确定了，那么它左边元素都比它小，右边都比它大。

//划分
int partion(int A[],int L,int R){
      int mid=A[L];
	while(L<R){
	//每一次划分:左边元素<枢轴元素<右边元素
	//R往前找，直到找到一个比mid小的元素，然后把A[R]放在A[L]的位置
       while(A[R]>=mid && L<R){
           R--;
       }
        A[L]=A[R];
		while(A[R]<=mid && L<R){
           L++;
       }
    	A[R]=A[L];
    }
    //存放枢轴元素
     A[L]=mid;
    return L；
}
//
void fun(int A[],int n){
	int M=0;
    int k=n/2;
    int L=0,R=n-1;
    while(1){
	M=partion(A,L,R);
	if(M==k-1) break;
        else if(M<k-1) L=M+1;
    	else R=M-1
    }
	//跳出循环说明已经找到第n/2小的元素

}