剖析栈和队列OJ题

news2024/9/27 7:19:28

1.括号匹配问题

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。
有效字符串需满足：
1.左括号必须用相同类型的右括号闭合。
2.左括号必须以正确的顺序闭合。
3.每个右括号都有一个对应的相同类型的左括号。

链接：https://leetcode.cn/problems/valid-parentheses/

思路分析

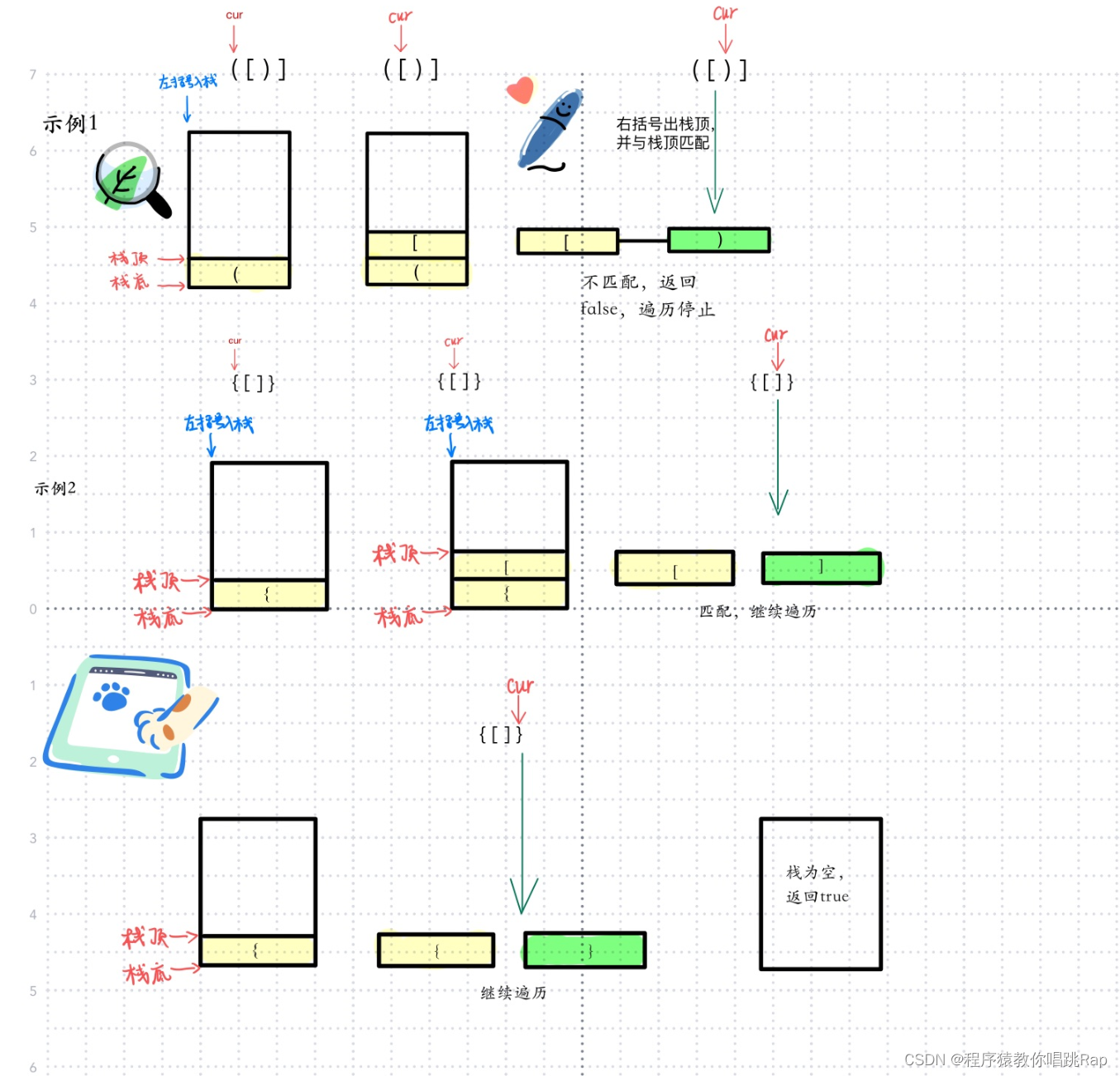
本题使用栈来做是最合适不过的，因为栈明确指出后进先出，先进后出。因此我们可以做一下考虑：
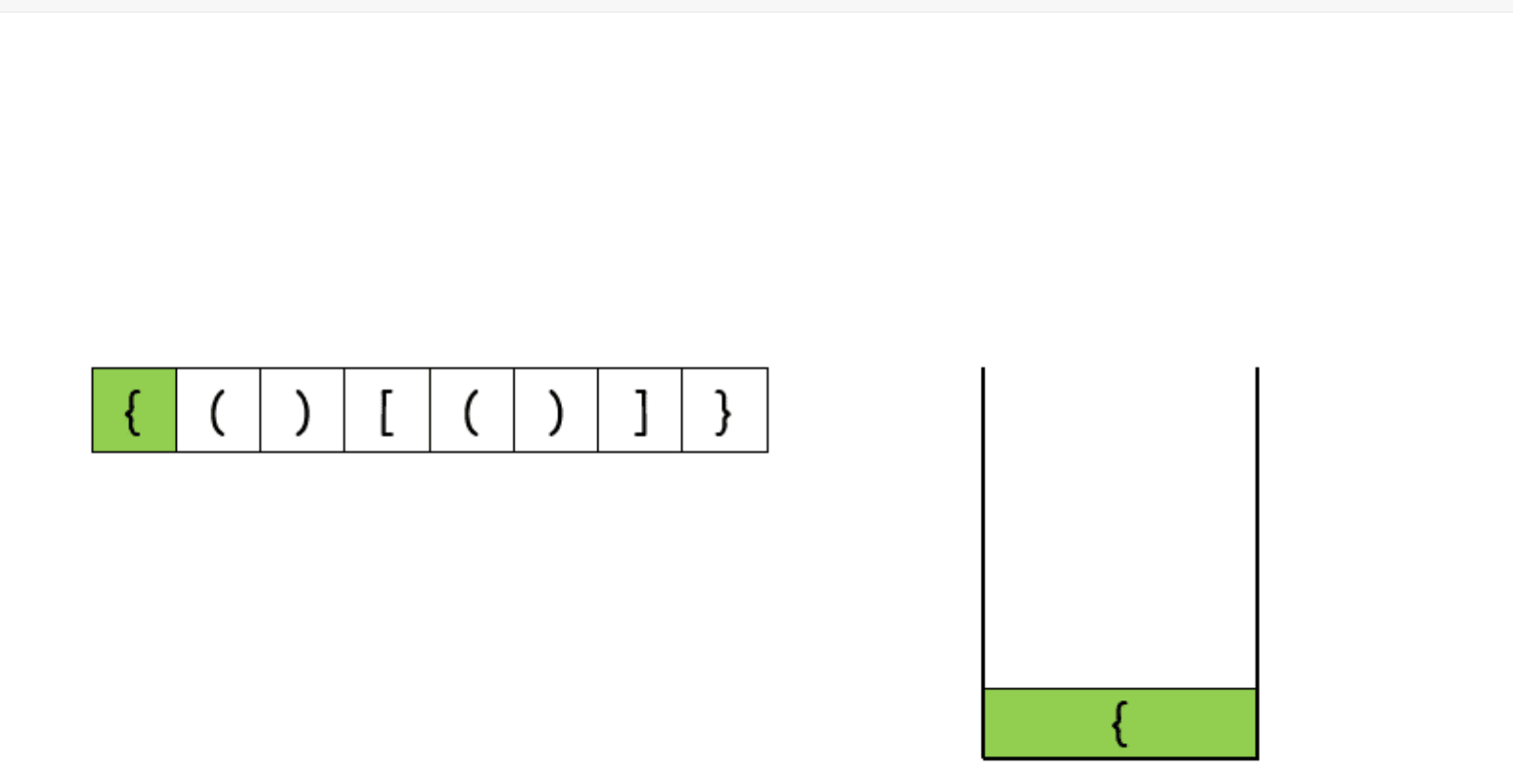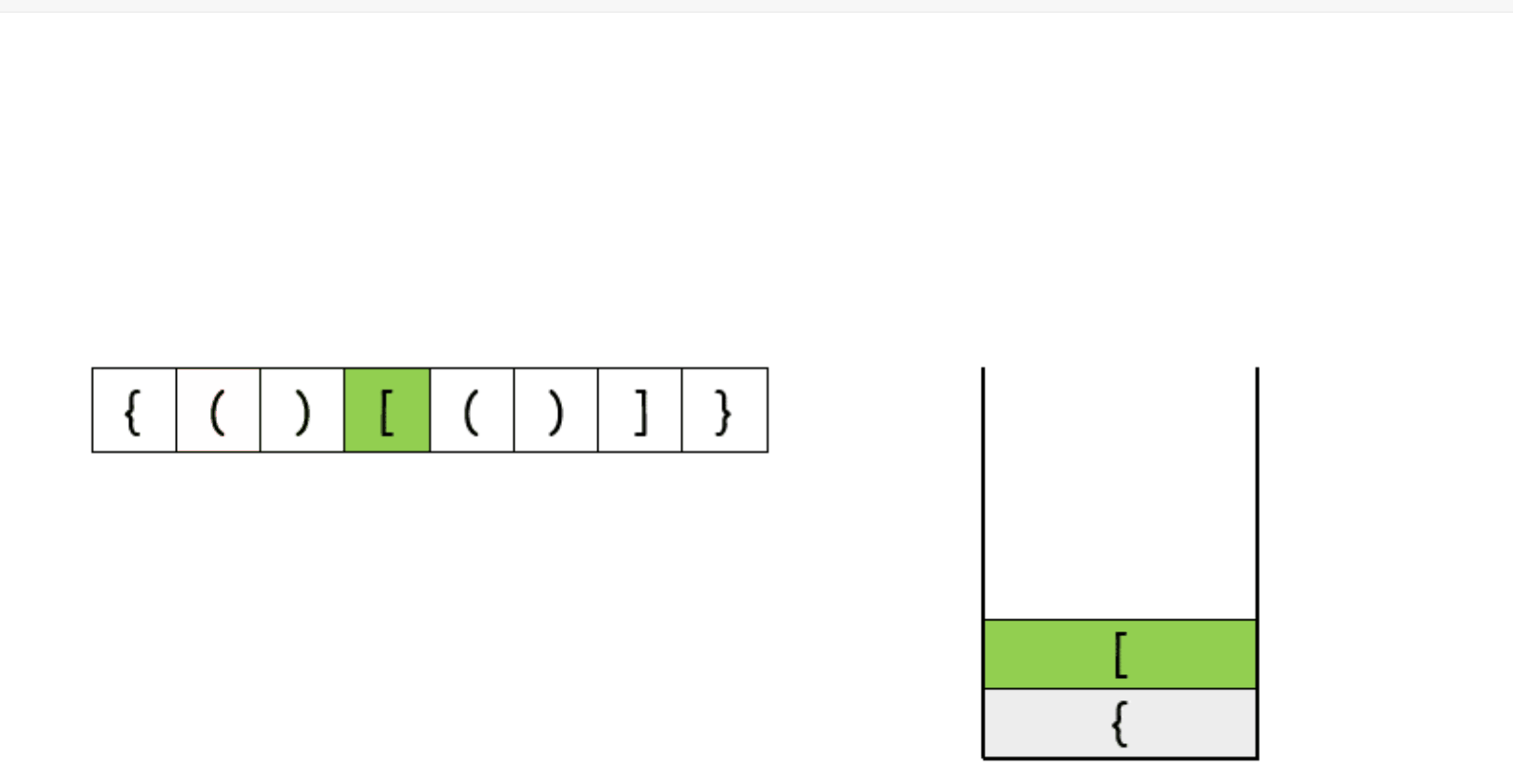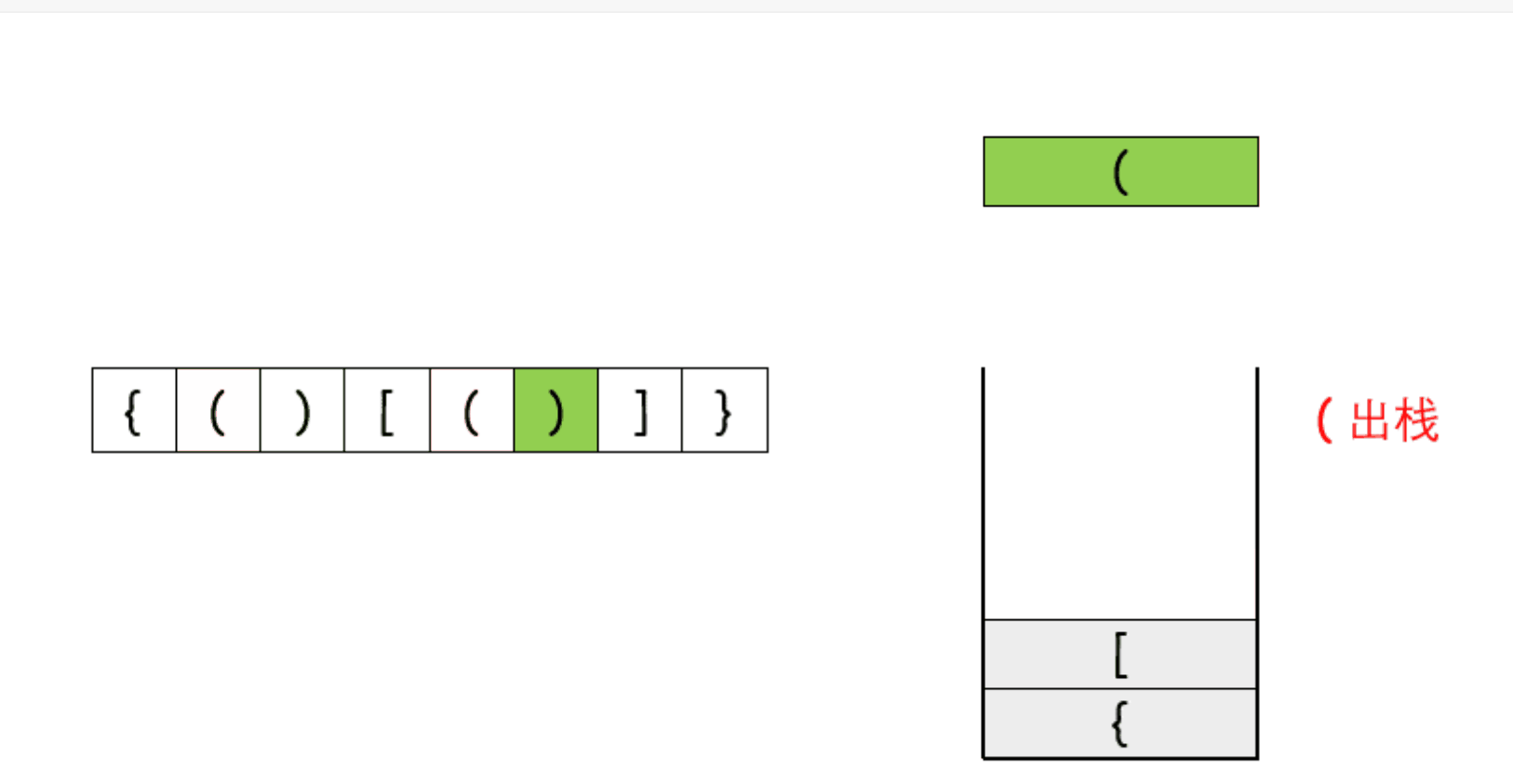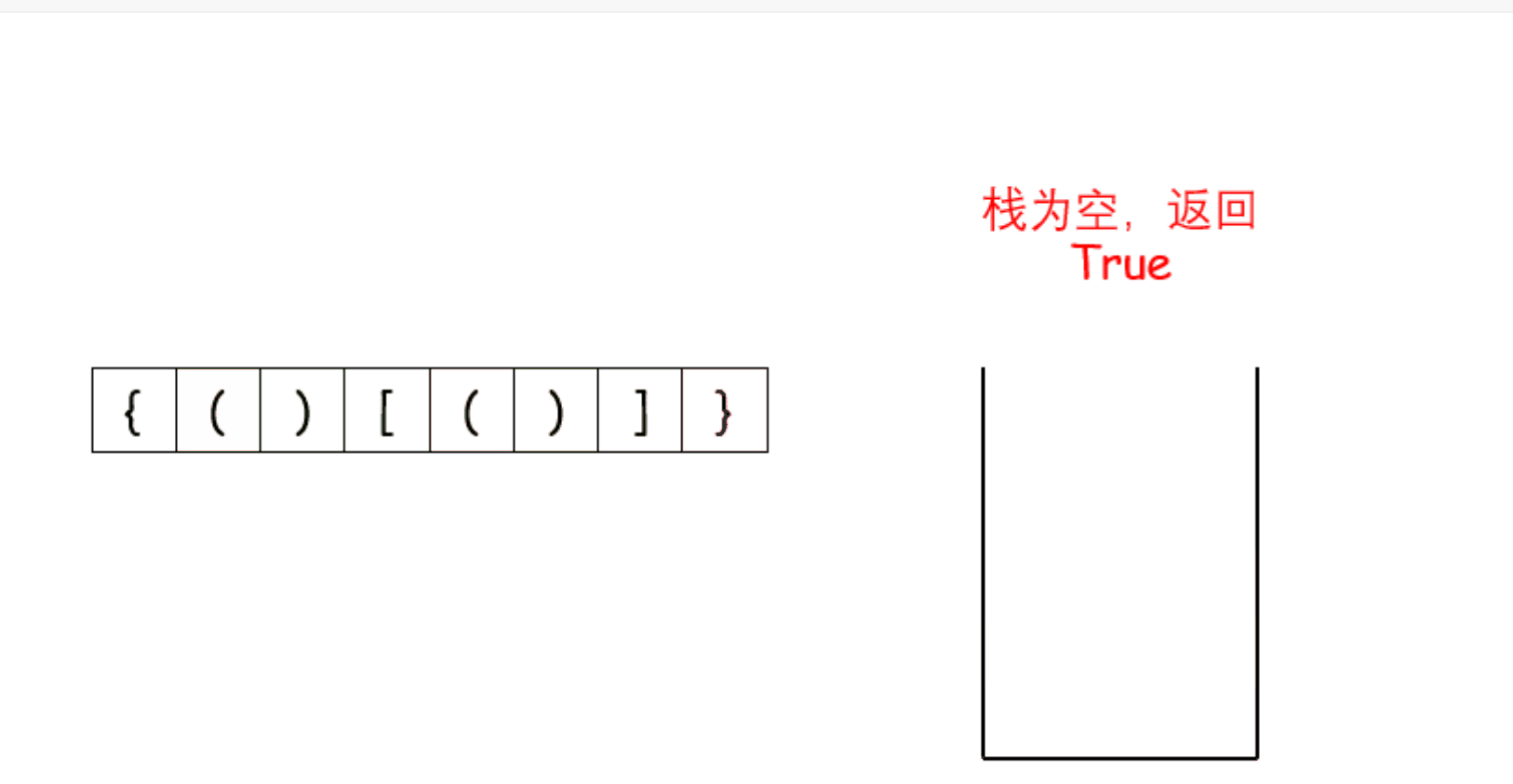
1.遇到左括号" ( ", " [ ", " { "，入栈
2.遇到右括号" ) ", " ] ", " } "，出栈，跟左括号要匹配，不匹配就报错。

参考代码

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
//创建栈结构
typedef char STDataType;
typedef struct stack
{
    STDataType* a;//存储数据
    int top;//栈顶位置
    int capacity;//容量
}ST;
void stackInit(ST* ps);//初始化
void stackDestroy(ST* ps);//销毁
void stackPush(ST* ps, STDataType x);//入栈
void stackPop(ST* ps);//出栈
STDataType stackTop(ST* ps);//取栈顶数据
int stackSize(ST* ps);//栈的有效元素个数
bool stackEmpty(ST* ps);//判断是否为空

//初始化 
void stackInit(ST* ps)
{
    assert(ps);
    ps->a = NULL;
    ps->top = 0;//指向初始值的下一个
    ps->capacity = 0;
}

//销毁
void stackDestroy(ST* ps)
{
    assert(ps);
    free(ps->a);
    ps->a = NULL;
    ps->capacity = ps->top = 0;
}

//入栈
void stackPush(ST* ps, STDataType x)
{
    assert(ps);
    if (ps->top == ps->capacity)
    {
        int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
        STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType)*newCapacity);
        if (tmp == NULL)
        {
            printf("realloc fail\n");
            exit(-1);
        }
        ps->a = tmp;
        ps->capacity = newCapacity;
    }
    ps->a[ps->top] = x;
    ps->top++;
}

//出栈
void stackPop(ST* ps)
{
    assert(ps);
    assert(ps->top > 0);
    ps->top--;
}

//判断是否为空
bool stackEmpty(ST* ps)
{
    assert(ps);
    return ps->top == 0;
}

//取栈顶数据
STDataType stackTop(ST* ps)
{
    assert(ps);
    assert(ps->top > 0);
    return ps->a[ps->top - 1];
}

//栈的有效元素个数
int stackSize(ST* ps)
{
    assert(ps);
    return ps->top;
}

//创建好了栈开始实现
bool isValid(char * s){
    ST st;//先创建一个栈
    stackInit(&st);//初始化栈
    while(*s)
    {
        if(*s=='('||*s=='['||*s=='{')
        {
            stackPush(&st,*s);//如果是左括号就入栈
            ++s;
        }
        else
        {
            if(stackEmpty(&st))
            {
                return false;//说明前面根本没有坐括号，导致栈为空，直接返回false
            }
            char top=stackTop(&st);//获取栈顶元素
            stackPop(&st);//出栈顶元素，接下来进行匹配
            if((*s==')'&&top!='(')||(*s==']'&&top!='[')||(*s=='}'&&top!='{'))
            {
                stackDestroy(&st);//销毁是为了防止内存泄漏
                return false;//如果不匹配，直接返回false
            }
            else
            {
                ++s;//此时匹配，接着继续比较，直到遍历结束
            }
        }
    }
    //栈为空，说明所有左括号都匹配
    bool ret=stackEmpty(&st);
    stackDestroy(&st);//防止内存泄漏
    return ret;
}

2.用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。
实现 MyStack 类：
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。
注意：
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

链接：https://leetcode.cn/problems/implement-stack-using-queues/

思路分析

首先要了解栈和队列的结构：
1.栈：后进先出
2.队列：先进先出
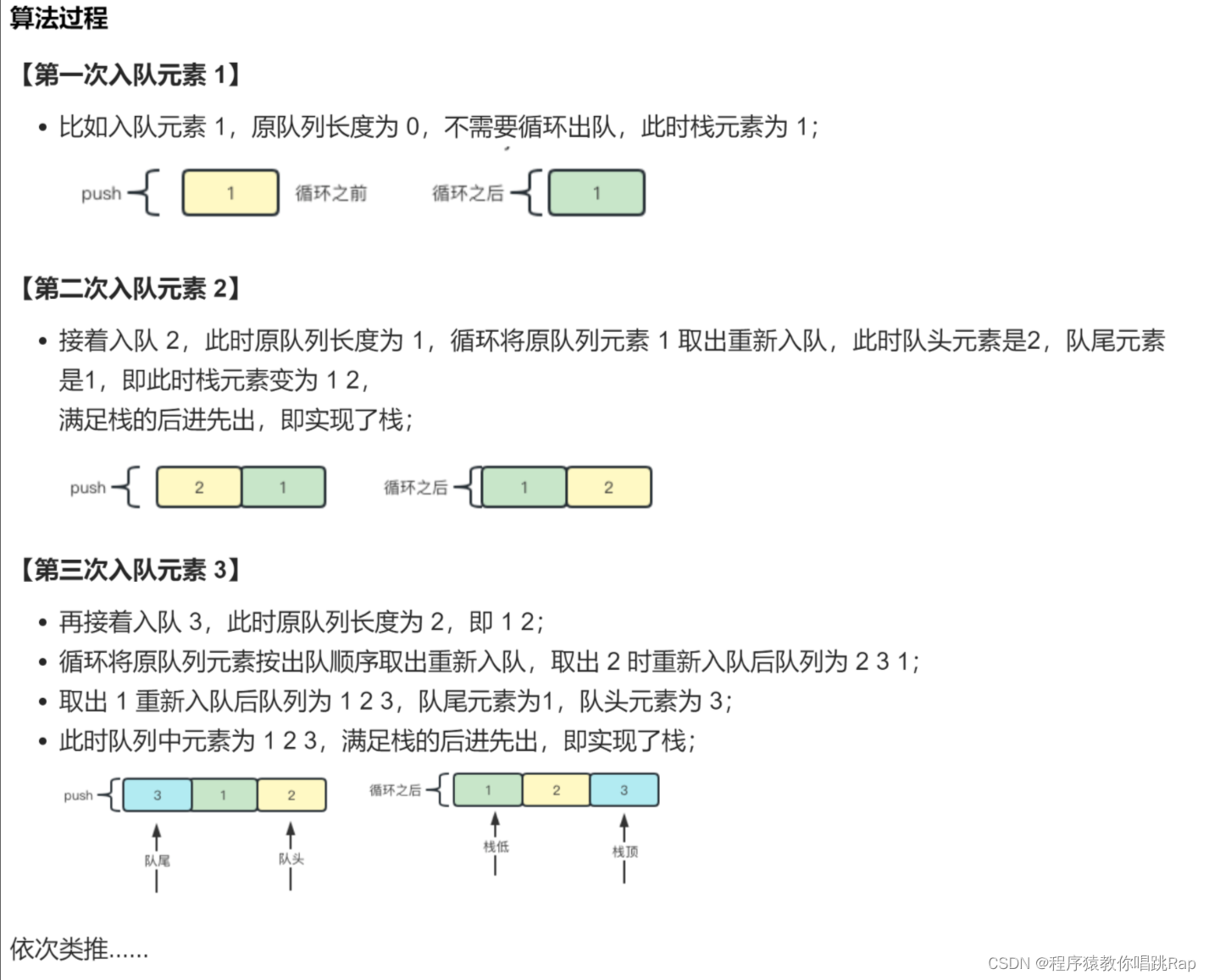
要是用队列实现栈就必须做到以下两步：
1.入栈：push数据到不为空的数据
2.出栈：把不为空队列的前n-1个导入到空队列中，最后将剩下的那个pop删掉。
核心：让一个队列先存储数据，另外一个队列空着，要出栈时，空队列用来导入数据（间接实现栈）

参考代码

//创建队列结构
typedef int QDataType;
//创建队列结点
typedef struct QueueNode
{
    struct QueueNode* next;//记录下一个结点
    QDataType data;//存储数据
}QNode;
//保存队头和队尾
typedef struct Queue
{
    QNode* head;//头指针
    QNode* tail;//尾指针
}Queue;
void QueueInit(Queue* pq);//初始化
void QueueDestroy(Queue* pq);//销毁
void QueuePush(Queue* pq, QDataType x);//入队列
void QueuePop(Queue* pq);//出队列
QDataType QueueFront(Queue* pq);//获取队头元素
QDataType QueueBack(Queue* pq);//获取队尾元素
int QueueSize(Queue* pq);//元素个数
bool QueueEmpty(Queue* pq);//判空

//初始化
void QueueInit(Queue* pq)
{
    assert(pq);
    pq->head = NULL;
    pq->tail = NULL;
}

//销毁
void QueueDestroy(Queue* pq)
{
    assert(pq);
    QNode* cur = pq->head;
    while (cur != NULL)
    {
        QNode* next = cur->next;
        free(cur);
        cur = next;
    }
    pq->head = pq->tail = NULL;
}

//判空
bool QueueEmpty(Queue* pq)
{
    assert(pq);
    return pq->head == NULL;
}

//入队列
void QueuePush(Queue* pq, QDataType x)
{
    assert(pq);
    //创建一个新结点保存数据
    QNode* newnode = (QNode*)malloc(sizeof(QNode));
    //暴力检测newnode,因为malloc的都要检测
    assert(newnode);
    newnode->next = NULL;
    newnode->data = x;
    //如果一开始没有数据，为空的情况
    if (pq->tail == NULL)
    {
        assert(pq->head == NULL);
        pq->head = pq->tail = newnode;
    }
    else
    {
        pq->tail->next = newnode;
        pq->tail = newnode;
    }
}

//出队列
void QueuePop(Queue* pq)
{
    assert(pq);
    assert(pq->head && pq->tail);//tail和head均不能为空
    //特殊：当删到head=tail位置时，tail会变成野指针
    if (pq->head->next == NULL)
    {
        free(pq->head);
        pq->head = pq->tail = NULL;
    }
    //一般情况
    else
    {
        //保存head的下一个结点
        QNode* next = pq->head->next;
        free(pq->head);
        pq->head = next;
    }
}

//获取队头元素
QDataType QueueFront(Queue* pq)
{
    assert(pq);
    assert(pq->head);//头部不能为空
    return pq->head->data;
}

//获取队尾元素
QDataType QueueBack(Queue* pq)
{
    assert(pq);
    assert(pq->tail);//尾部不能为空
    return pq->tail->data;
}

//获取有效元素个数
int QueueSize(Queue* pq)
{
    assert(pq);
    int n = 0;
    QNode* cur = pq->head;
    while (cur)
    {
        ++n;
        cur = cur->next;
    }
    return n;
}
// *******************************************************************/


typedef struct {
    Queue q1;//队列1
    Queue q2;//队列2
} MyStack;


MyStack* myStackCreate() {
    MyStack* pst=(MyStack*)malloc(sizeof(MyStack));//申请一个MyStack类型的栈
    assert(pst);
    QueueInit(&pst->q1);//初始化队列1
    QueueInit(&pst->q2);//初始化队列2
    return pst;
}

void myStackPush(MyStack* obj, int x) {
    assert(obj);
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);//如果q1不为空，就往q1插入数据
    }
    else
    {
        QueuePush(&obj->q2,x);//这里直接push
    }
}

int myStackPop(MyStack* obj) {
    assert(obj);
    Queue* emptyQ=&obj->q1;//默认q1为空
    Queue* nonEmtpyQ=&obj->q2;//默认q2不为空
    if(!QueueEmpty(&obj->q1))
    {
        emptyQ=&obj->q2;//若假设错误，则q2为空
        nonEmtpyQ=&obj->q1;//此时q1就为空       
    }
    while(QueueSize(nonEmtpyQ)>1)
    {
        QueuePush(emptyQ,QueueFront(nonEmtpyQ));//把非空的导入空的队列，直到剩下最后一个
        QueuePop(nonEmtpyQ);//此时把非空的队头数据删掉，便于后面导入数据
    }
    int top=QueueFront(nonEmtpyQ);//记录此时的栈顶数据
    QueuePop(nonEmtpyQ);//删除栈顶数据，置空队列
    return top;
}

int myStackTop(MyStack* obj) {
    assert(obj);
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);//如果q1不为空，返回
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
    assert(obj);
    //两个队列均为空，则为空
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    assert(obj);
    QueueDestroy(&obj->q1);//释放q1
    QueueDestroy(&obj->q2);//释放q2
    free(obj);
}

3.用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
实现 MyQueue 类：
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false
说明：
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

链接：https://leetcode.cn/problems/implement-queue-using-stacks/

思路分析

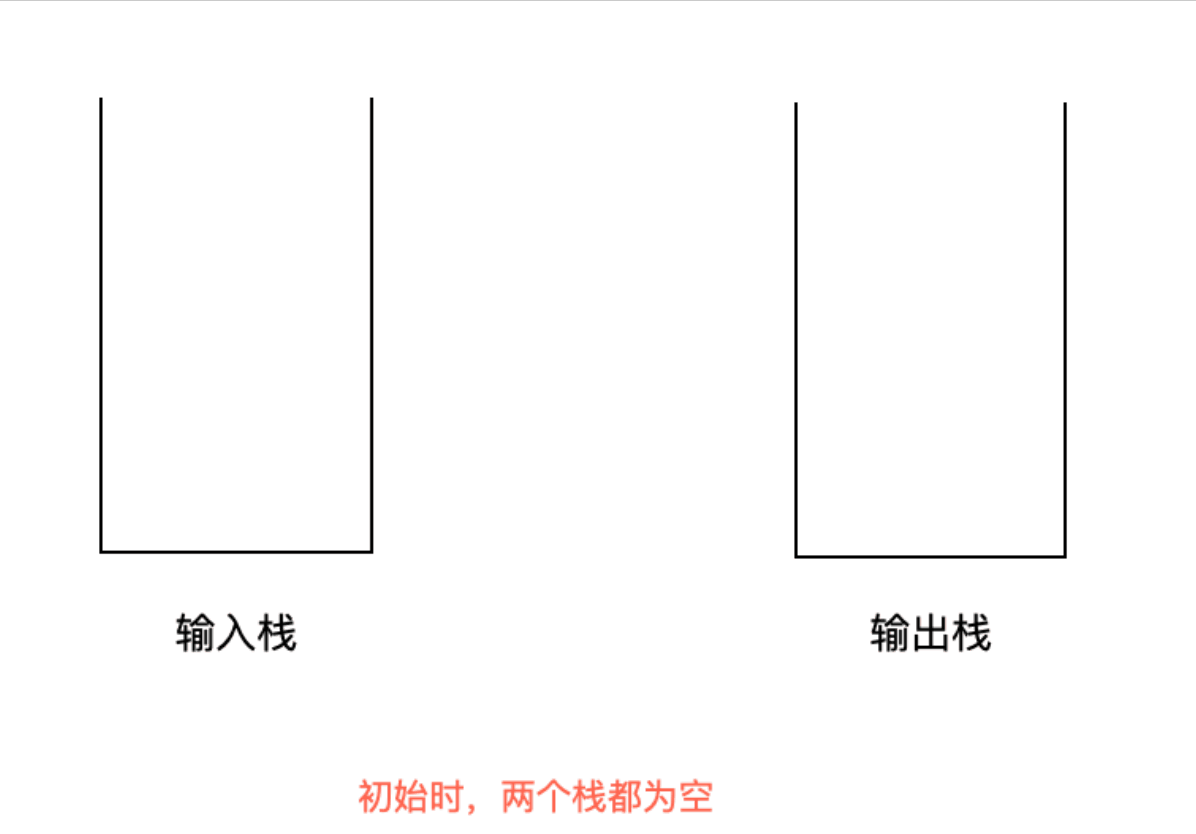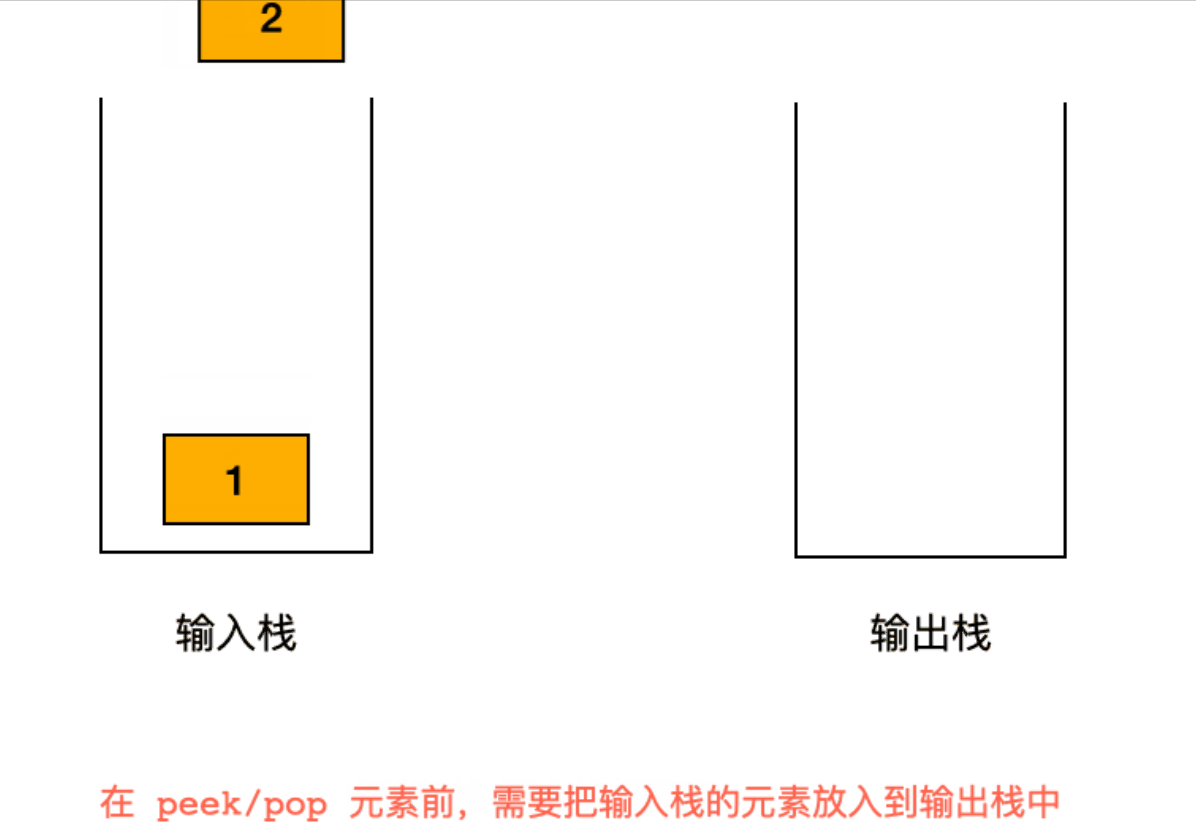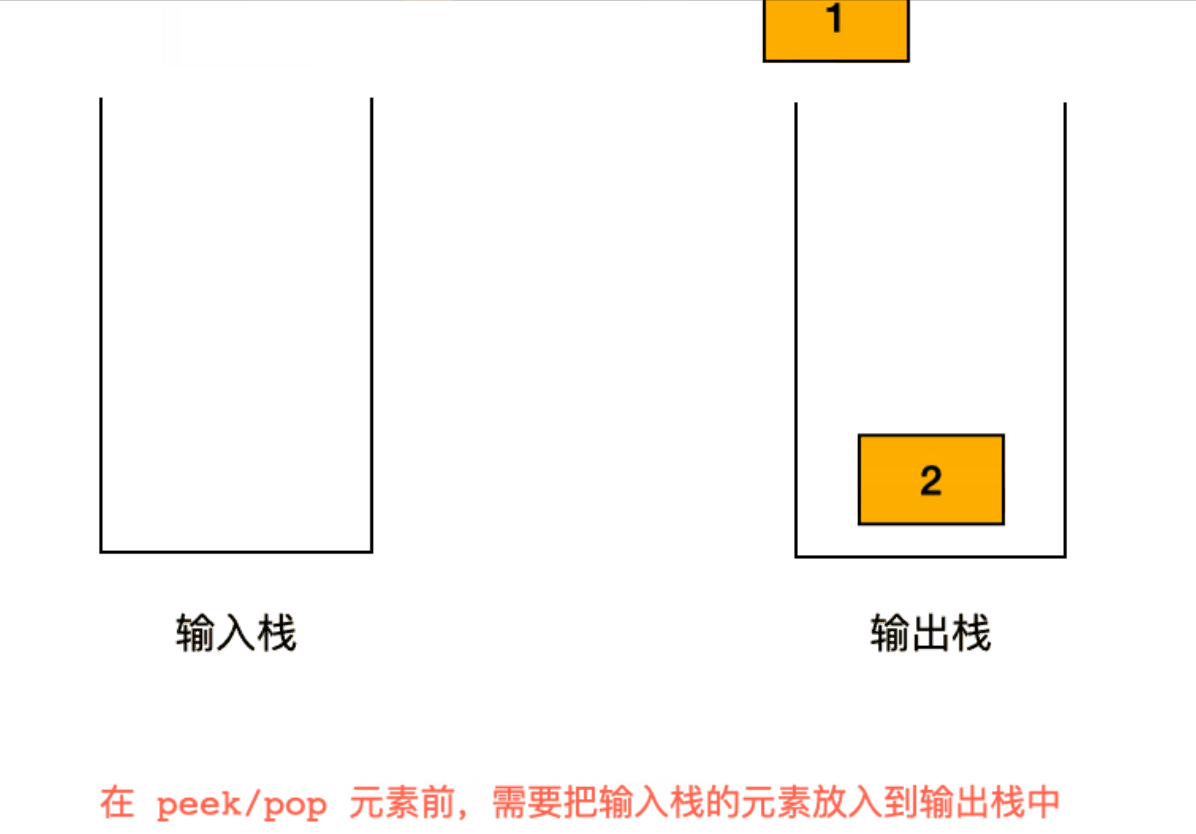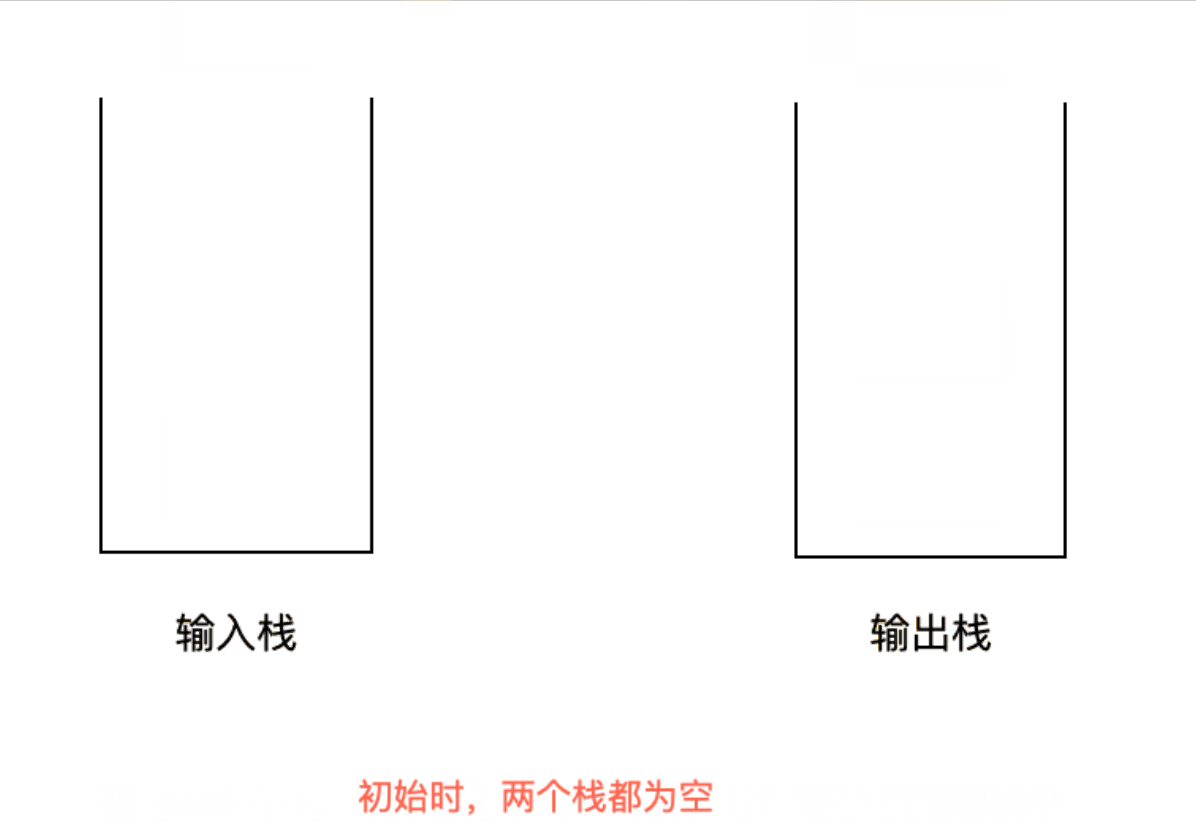
题目让我们用两个栈来实现一个队列，就是要让两个栈实现一个先进先出的数据结构。
思路是：「输入栈」会把输入顺序颠倒；如果把「输入栈」的元素逐个弹出放到「输出栈」，再从「输出栈」弹出元素的时候，则可以负负得正，实现了先进先出。
具体做法：
可以把一个栈当做「输入栈」，把另一个栈当做「输出栈」。
当 push() 新元素的时候，放到「输入栈」的栈顶，记此顺序为「输入序」。
当 pop() 元素的时候，是从「输出栈」弹出元素。如果「输出栈」为空，则把「输入栈」的元素逐个 pop() 并且 push() 到「输出栈」中，这一步会把「输入栈」的栈底元素放到了「输出栈」的栈顶。此时负负得正，从「输出栈」的 pop() 元素的顺序与「输入序」相同。

参考代码

//创建栈的结构
typedef int STDataType;
typedef struct stack
{
    STDataType* a;
    int top;
    int capacity;
}ST;
void stackInit(ST* ps);//初始化
void stackDestroy(ST* ps);//销毁
void stackPush(ST* ps, STDataType x);//入栈
void stackPop(ST* ps);//出栈
STDataType stackTop(ST* ps);//取栈顶数据
int stackSize(ST* ps);//栈的大小
bool stackEmpty(ST* ps);//判断是否为空

void stackInit(ST* ps)
{
    assert(ps);
    ps->a = NULL;
    ps->top = 0;//指向初始值的下一个
    ps->capacity = 0;
}

void stackDestroy(ST* ps)
{
    assert(ps);
    free(ps->a);
    ps->a = NULL;
    ps->capacity = ps->top = 0;
}

void stackPush(ST* ps, STDataType x)
{
    assert(ps);
    if (ps->top == ps->capacity)
    {
        int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
        STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType)*newCapacity);
        if (tmp == NULL)
        {
            printf("realloc fail\n");
            exit(-1);
        }
        ps->a = tmp;
        ps->capacity = newCapacity;
    }
    ps->a[ps->top] = x;
    ps->top++;
}

void stackPop(ST* ps)
{
    assert(ps);
    assert(ps->top > 0);
    ps->top--;
}

bool stackEmpty(ST* ps)
{
    assert(ps);
    return ps->top == 0;
}

STDataType stackTop(ST* ps)
{
    assert(ps);
    assert(ps->top > 0);
    return ps->a[ps->top - 1];
}

int stackSize(ST* ps)
{
    assert(ps);
    return ps->top;
}

/******************************************************/


typedef struct {
    ST pushST;//插入数据的栈
    ST popST;//删除数据的栈
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));//申请队列类型
    assert(obj);
    stackInit(&obj->pushST);//初始化pushST
    stackInit(&obj->popST);//初始化popST
    return obj;
}

void myQueuePush(MyQueue* obj, int x) {
    assert(obj);
    stackPush(&obj->pushST,x);//无论有没有数据，都要插入
}

int myQueuePop(MyQueue* obj) {
    assert(obj);
    if(stackEmpty(&obj->popST))//如果popST数据为空，要从pushST里导入数据才能删除
    {
        while(!stackEmpty(&obj->pushST))//pushST数据不为空，就一直向popST里面导入数据
        {
            stackPush(&obj->popST,stackTop(&obj->pushST));//把pushST栈顶数据导入到popST里
            stackPop(&obj->pushST);//删除popST栈顶元素，实现队列先进先出
            
        }
    }
    int front=stackTop(&obj->popST);//记录popST栈顶元素
    stackPop(&obj->popST);//删除popST栈顶元素，实现队列先进先出
    return front;//返回栈顶数据
}

int myQueuePeek(MyQueue* obj) {
    assert(obj);
    //如果popST数据为空，要从pushST里导入数据才能取到队头数据
    if(stackEmpty(&obj->popST))
    {
        while(!stackEmpty(&obj->pushST))//pushST数据不为空，就一直向popST里导入数据
        {
            stackPush(&obj->popST,stackTop(&obj->pushST));//把pushST栈顶数据导入到popST里
            stackPop(&obj->pushST);//导完后把pushST栈顶元素删掉，便于后面继续导
        }
    }
    return stackTop(&obj->popST);//直接返回栈顶元素
}

bool myQueueEmpty(MyQueue* obj) {
    return stackEmpty(&obj->pushST)&&stackEmpty(&obj->popST);
}

void myQueueFree(MyQueue* obj) {
    assert(obj);
    stackDestroy(&obj->pushST);
    stackDestroy(&obj->popST);
    free(obj);
}

4.设计循环队列

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。
你的实现应该支持如下操作：
MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

链接：https://leetcode.cn/problems/design-circular-queue/

思路分析

参考代码

typedef struct {
    int* a; //用数组模拟环形队列
    int front;//队头
    int tail; //队尾
    int k; //表示存的数据长度为k
} MyCircularQueue;
 
bool myCircularQueueIsFull(MyCircularQueue* obj); //前置声明
bool myCircularQueueIsEmpty(MyCircularQueue* obj);//前置声明
 
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));//创建环形链表结构
    assert(obj);
    obj->a = (int*)malloc(sizeof(int) * (k + 1));//多开一个空间，便于后续区分空或满
    obj->front = obj->tail = 0;
    obj->k = k; //队列存储有效数据长度为k
    return obj;
}
 
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (myCircularQueueIsFull(obj))
    {
        return false; //队列已满，不能插入数据
    }
    obj->a[obj->tail] = value; //赋值
    if (obj->tail == obj->k)
    {
        obj->tail = 0; //当tail走到尾端
    }
    else
    {
        obj->tail++;
    }
    return true;
}
 
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return false; //队列为空，不能删除
    }
    if (obj->front == obj->k)
    {
        obj->front = 0; //当front走到尾端
    }
    else
    {
        obj->front++;
    }
    return true;
}
//取头
int myCircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1; //队列为空，取不了
    }
    return obj->a[obj->front]; //返回队头
}
//取尾
int myCircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1; //队列为空，取不了
    }
    if (obj->tail == 0)
    {
        return obj->a[obj->k]; //tail为0，队尾在长度的最后一个位置
    }
    else
    {
        return obj->a[obj->tail - 1];
    }
}
 
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->tail; //front==tail时为空
}
 
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    if (obj->tail == obj->k && obj->front == 0)
    {
        return true; //当tail尾端，front在头端时也是满
    }
    else
    {
        return obj->tail + 1 == obj->front; //一般情况，当tail的下一个位置为front时为满
    }
}
 
void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/170379.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【阅读笔记】c++ Primer Plus——第八章

【阅读笔记】c++ Primer Plus——第八章

函数探幽 c内联函数 为了提高程序运行速度而做的改进编译的最终产物是可执行程序——由一组机器语言指令组成。运行程序时&#xff0c;操作系统将这些指令载入到计算机内存中&#xff0c;因此每条指令都有特定的内存地址。然后计算机开始逐步执行指令。执行到函数调用的时候&…
阅读更多...
一道编程劝退题，检测你是否适合干编程

一道编程劝退题，检测你是否适合干编程

前言大家都知道要想成为一名优秀的开发工程师&#xff0c;需要数学基础好&#xff0c;即你要有很强的逻辑思维能力&#xff0c;这里有一道美国斯坦福大学出的一道逻辑思维的测试测试&#xff0c;检测你的逻辑思维能力&#xff0c;大家可以看看自己逻辑能力怎么样。题目有一个抽…
阅读更多...
＜队列＞的概念结构实现【C语言版】

＜队列＞的概念结构实现【C语言版】

1.队列的概念及结构 队列对于临时数据的处理也十分有趣&#xff0c;它跟栈一样都是有约束条件的数组&#xff08;或者链表&#xff09;。区别在于我们想要按什么顺序去处理数据&#xff0c;而这个顺序当然是要取决于具体的应用场景。 你可以将队列想象成是电影院排队。排在最…
阅读更多...
Android Studio 工程导入 AOSP编译的 android.jar

Android Studio 工程导入 AOSP编译的 android.jar

使用场景 　　1.需要使用 framework 中的 SystemApi 文件或者 hide 的 API 接口 　　2.定制 Framework 层业务&#xff0c;即有 客制化 的 API 接口 补充知识点 　　1.framework 源码即 AS 工程目录中 External Libraries 下的 < Android API xx Platform > 下的原生 SDK…
阅读更多...
Docker-全面详解（学习总结---从入门到深化）

Docker-全面详解（学习总结---从入门到深化）

一、什么是Docker Docker 是一个开源的应用容器引擎&#xff0c;基于 Go 语言 并遵从 Apache2.0 协议开源。 什么是"集装箱技术" 我们都知道码头里的集装箱是运载货物用的&#xff0c;它是一种按规格标准 化的钢制箱子。集装箱的特色&#xff0c;在于其格式划一&…
阅读更多...
峰值21WQps、亿级DAU，小游戏《羊了个羊》是怎么架构的？

峰值21WQps、亿级DAU，小游戏《羊了个羊》是怎么架构的？

小游戏《羊了个羊》 短短的7天内&#xff0c;DAU突破了1亿、吞吐量峰值21WQps。 《羊了个羊》运营后台数据显示&#xff0c;在短短的7天内&#xff0c;这款小游戏的DAU就突破了1亿。 要知道&#xff0c;除了王者荣耀、原神等屈指可数的现象级手游之外&#xff0c;1亿DAU是这个…
阅读更多...
LeetCode刷题模版：131 - 140

LeetCode刷题模版：131 - 140

目录 简介131. 分割回文串132. 分割回文串 II133. 克隆图134. 加油站135. 分发糖果136. 只出现一次的数字137. 只出现一次的数字 II138. 复制带随机指针的链表139. 单词拆分140. 单词拆分 II【未理解】结语简介 Hello！ 非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您…
阅读更多...
【GitHub仓库上传和克隆】

【GitHub仓库上传和克隆】

GitHub仓库上传和克隆1. 安装1.1 WindowR:cmd1.2 选择写代码的文件夹右键Git Bash Here1.3 分支管理2. 本地仓库推送给网络仓库2.1 忽略推送文件2.2 本地初始推送3. 克隆3.1 克隆下载3.2 克隆代码修改上传3.2.1 初次推送3.2. 2 后续推送其他1. 安装 1.1 WindowR:cmd //是否安…
阅读更多...
Redis从入门到精通（一：Redis入门）

Redis从入门到精通（一：Redis入门）

Redis 简介 问题现象 海量用户 高并发 罪魁祸首——关系型数据库性能瓶颈&#xff1a;磁盘IO性能低下扩展瓶颈&#xff1a;数据关系复杂&#xff0c;扩展性差&#xff0c;不便于大规模集群解决思路降低磁盘IO次数&#xff0c;越低越好 —— 内存存储去除数据间关系&#xff0…
阅读更多...
ucore lab1,lab2,lab3,lab4链表详解 获取结构体成员偏移

ucore lab1,lab2,lab3,lab4链表详解 获取结构体成员偏移

ucore版链表介绍 ucore是清华大学操作系统实验课要完成的操作系统&#xff0c;里面有个链表数据结构我觉得很有意思&#xff0c;记录下来。 ucore将链表与数据对象分离&#xff0c;使得任意数据对象&#xff0c;只要加上一个链表组件就能组织成一个链表。 要使得一个本来不具…
阅读更多...
双目相机国产、非国产统计参数对比分析

双目相机国产、非国产统计参数对比分析

双目相机国产、非国产统计参数对比分析 ZED ZED是STEREOLABS出品的双目摄像头&#xff0c;广泛应用在科研机构的无人车、协作机械臂上&#xff0c;如图2-1所示。其3D分辨率在Ultra模式下可达到RGB时的分辨率&#xff0c;具体见图2-2&#xff0c;物理尺寸为1753033mm&#xff…
阅读更多...
记录一次gateway HandlerStrategies.withDefaults().messageReaders() 导致的内存炸裂的问题

记录一次gateway HandlerStrategies.withDefaults().messageReaders() 导致的内存炸裂的问题

背景 年前出现了一次内存炸裂的生产事故。导致其他请求无法请求通过。 [boundedElastic-55] [Loggers.java:314]:Scheduler worker in group main failed with an uncaught exception [TID:] 2023-01-18 10:40:33.189 [INFO] [boundedElastic-55] [AccessTokenGatewayFilterF…
阅读更多...
Arduino基础学习——meArm（太极创客第二部分）

Arduino基础学习——meArm（太极创客第二部分）

面包板电源模块为机器臂单独供电&#xff0c;机器臂本身有四个小电机驱动作用&#xff0c;如果单独靠arduino来为这四个小电机供电&#xff0c;机器臂可能不会稳定工作&#xff0c;将会抖动。 机械臂的四个动作主要靠四个电机来控制&#xff0c;这四个电机主要连接在我们的ard…
阅读更多...
云端IDE系列教程4：TitanIDE + Typora = 鱼和熊掌

云端IDE系列教程4：TitanIDE + Typora = 鱼和熊掌

概述 目前&#xff0c;大部分技术人员使用 Markdown 编写技术文档已经成了日常工作的一部分&#xff0c;现在市场上也有各种各样的文字编辑工具&#xff1a;石墨文档、有道云笔记、语雀、金山文档、腾讯文档、Google文档&#xff0c;WPS、Office、Typora等。但在云原生时代&am…
阅读更多...
vue3学习笔记(总)——ts+组合式API(setup语法糖)

vue3学习笔记(总)——ts+组合式API(setup语法糖)

文章目录1. ref全家桶1.1 ref()1.2 isRef()以及isProxy()1.3 shallowRef()1.4 triggerRef()1.5 customRef()1.6 unref()2. reactive全家桶2.1 reactive()2.2 readonly()2.3 shallowReactive() 和 shallowReadonly()3. to系列全家桶3.1 toRef()3.2 toRefs()3.3 toRaw()4. comput…
阅读更多...
【年度总结】回看2022，展望2023，做更好的自己

【年度总结】回看2022，展望2023，做更好的自己

作者主页&#xff1a;Designer 小郑 作者简介&#xff1a;Java全栈软件工程师一枚&#xff0c;来自浙江宁波&#xff0c;负责开发管理公司OA项目&#xff0c;专注软件前后端开发&#xff08;Vue、SpringBoot和微信小程序&#xff09;、系统定制、远程技术指导。CSDN学院、蓝桥云…
阅读更多...
Mac 下ZooKeeper安装和使

Mac 下ZooKeeper安装和使

Mac 下ZooKeeper安装和使用 Apache ZooKeeper分布式协调系统是构建分布式应用程序的高性能服务。 1.下载ZooKeeper 环境要求&#xff1a;ZooKeeper服务器是用Java创建的&#xff0c;它运行在JVM之上。需要安装JDK 7或更高版本。 https://zookeeper.apache.org/releases.html …
阅读更多...
1.3 PCIe——硬件实现架构

1.3 PCIe——硬件实现架构

PCIe的设计可以分为controller和PHY&#xff0c;整体设计较为复杂&#xff0c;一般可向IP厂商定制设计&#xff0c;controller和PHY模块的接口是PIPE接口 一、一般实现架构 1.1 PCIE controller 控制器逻辑包含了IP的host设计&#xff0c;以及PCIe协议中所规定的事务层、数…
阅读更多...
AirServer电脑投屏软件免费版使用及切换中文教程

AirServer电脑投屏软件免费版使用及切换中文教程

AirServer是由App Dynamic打造的一款投屏软件。AirServer是适用于Mac和Windows的先进的屏幕镜像接收器。可以将手机设备&#xff0c;如iPhone、iPad、安卓上的屏幕投送到电脑屏幕上。特别我们日常开会要给客户演示手机上的操作时&#xff0c;投屏就显得非常专业。当然&#xff…
阅读更多...
关于java位移运算的一点讨论

关于java位移运算的一点讨论

框架乱飞的年代&#xff0c;时常还得往框架源码里看&#xff0c;对内在原理没点理解&#xff0c;人家就会认为你不太行。平时开发你可能没咋用过位移运算&#xff0c;但往源码里一看&#xff0c;就时常能看到它。我也是看着看着&#xff0c;突然仔细一琢磨&#xff0c;又不由得…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023