本博客需要对位置编码有一定了解，但不熟悉代码实现的老哥看。

正弦位置编码（sinusoidal）

在介绍RoPE之前，先回顾一下正弦位置编码。

数学表达

$$PE(pos,2i)=sin(\frac{pos}{10000^{2i/d_{model}}})$$
$$PE(pos,2i+1)=cos(\frac{pos}{10000^{2i/d_{model}}})$$
上面两个公式是正弦位置编码的数学表达式，其中

• $pos$表示位置，比如长度为68的序列，$pos\in [0,67)$
• $d_{model}$表示位置编码的维度（模型的宽度、模型的特征维度、模型隐藏层的维度），比如设置位置编码的维度是100。
• $i$表示位置编码在$d_{model}$维度上两两分组的编号，$i\in [0,d_{model}//2-1]$，一定要强化这个概念，$i$表示的是$d_{model}$维度上两两分组的编号。
• 可以命名${\theta }_i=\frac{1}{10000^{2i/d_{model}}}=\frac{1}{10000^{i/(d_{model}/2)}}$，所以上面两个公式可以看做是位置$pos$和分组变量$i$的函数。

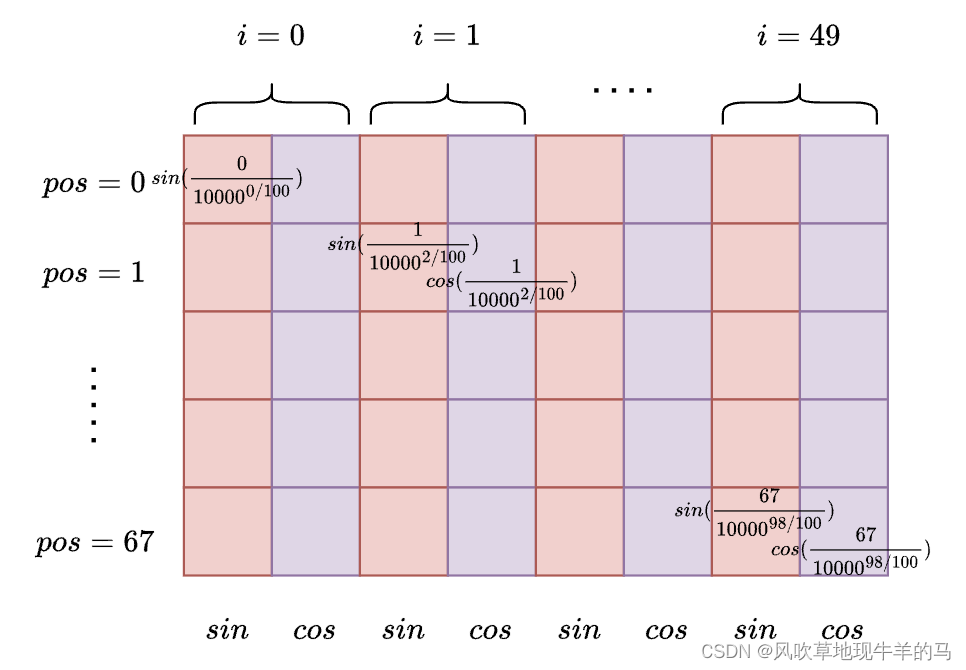
可以将上述两个公式看做是二维平面，比如，将$i$看做横坐标，将$pos$看做纵坐标。并且需要注意，上述矩阵，每一个位置都是有值的。

代码实现

import torch
import torch.nn as nn

def get_SinPositionEncoding(max_sequence_length, d_model, base=10000):
    # [max_sequence_length, d_model]
    pe = torch.zeros(max_sequence_length, d_model, dtype=torch.float)

    # [0, 1, 2, ... ,d_model//2-1]   shape = [d_model//2]
    ids_x = torch.arange(d_model // 2, dtype=torch.float)  # 获得相当于x维度的ids，取值是 [0, d_model//2-1]
    exp_value = ids_x / (d_model / 2)  # 获得base的指数幂次

    alpha = 1 / (base ** exp_value)
    # a^x = e^{x*ln(a)}
    # alpha = torch.exp(torch.arange(0, self.d_model, 2) * -(math.log(self.base) / self.d_model))

    # [0, 1, 2, ..., max_sequence_length-1]   shape = [max_sequence_length]
    pos_y = torch.arange(max_sequence_length, dtype=torch.float)

    inputs = pos_y[:, None] @ alpha[None, :]  # @表示矩阵乘法，*表示对应元素乘
    embedding_sin = torch.sin(inputs)
    embedding_cos = torch.cos(inputs)

    pe[:, 0::2] = embedding_sin  # 偶数位置设置为sin
    pe[:, 1::2] = embedding_cos  # 奇数位置设置为cos
    return pe

RoPE位置编码

数学表达

在介绍RoPE的数学表达之前，需要了解，RoPE是应用在计算attention scores之前的一步进行的。RoPE通过在q和k向量上应用RoPE，使得应用RoPE之后的q和k有位置信息。

• 未应用RoPE的query和key向量记为：$q,k$
• 应用RoPE之后的query和key向量记为：$q_{rope},k_{rope}$，有$q_{rope}=RoPE(q),k_{rope}=RoPE(k)$
• 计算attention score:
  $$attentionscore=q_{rope}{k}_{rope}^T$$
  这里计算的attention score里面就融合了相对位置信息，之后的计算流程和传统的self attention的计算流程无差别。

接下来看下，前面提到的RoPE函数如何实现？在正弦位置编码那一节提到，正弦位置编码其实是位置$pos$和分组变量$i$的函数，那么RoPE也是如此。

假设第$m$个token（位置是$m$）的query和key向量分别是$q和k$，对于$d$维的$q$向量来说，$q_{rope}$是通过下面的公式获得的：

• 在上式中，左侧矩阵记为$R_{\theta }^q$，其维度是$d\ast d$维的矩阵，右侧列向量表示query向量。
• 红色框，表示一组分组，编号记为$i$，$i\in [0,d//2-1]$
• ${\theta }_i=\frac{1}{10000^{2i/d_{model}}}=\frac{1}{10000^{i/(d_{model}/2)}}$ ，该定义与正弦位置编码一节的定义相同。

本博客没有涉及到复数运算等数学内容，从结果到原因，若需要由原因到结果，网络上有很多讲解清楚的博客。

由于矩阵的稀疏性，会造成计算上的浪费，所以在计算时采用逐位相乘再相加的方式进行：
$$\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\\ ..\\ q_{d-2}\\ q_{d-1}\end{array}\right]\ast \left[\begin{array}{c}cosm{\theta }_0\\ cosm{\theta }_0\\ cosm{\theta }_1\\ cosm{\theta }_1\\ ..\\ cosm{\theta }_{d/2-1}\\ cosm{\theta }_{d/2-1}\end{array}\right]+\left[\begin{array}{c}-q_1\\ q_0\\ -q_3\\ q_2\\ ..\\ -q_{d-1}\\ q_{d-2}\end{array}\right]\ast \left[\begin{array}{c}sinm{\theta }_0\\ sinm{\theta }_0\\ sinm{\theta }_1\\ sinm{\theta }_1\\ ..\\ sinm{\theta }_{d/2-1}\\ sinm{\theta }_{d/2-1}\end{array}\right](1)$$

• 在公式(1)中，记$cos$那一列是$cos(m,\theta )$，$sin$那一列是$sin(m,\theta )$，第三列query那一列记为$q_{inv}$，
  所以，最终，$RoPE$的实现非常简单，
  $$q\ast cos(m,\theta )+q_{inv}\ast sin(m,\theta )(2)$$

那么如何获得对于的$cos(m,\theta )$与$sin(m,\theta )$？

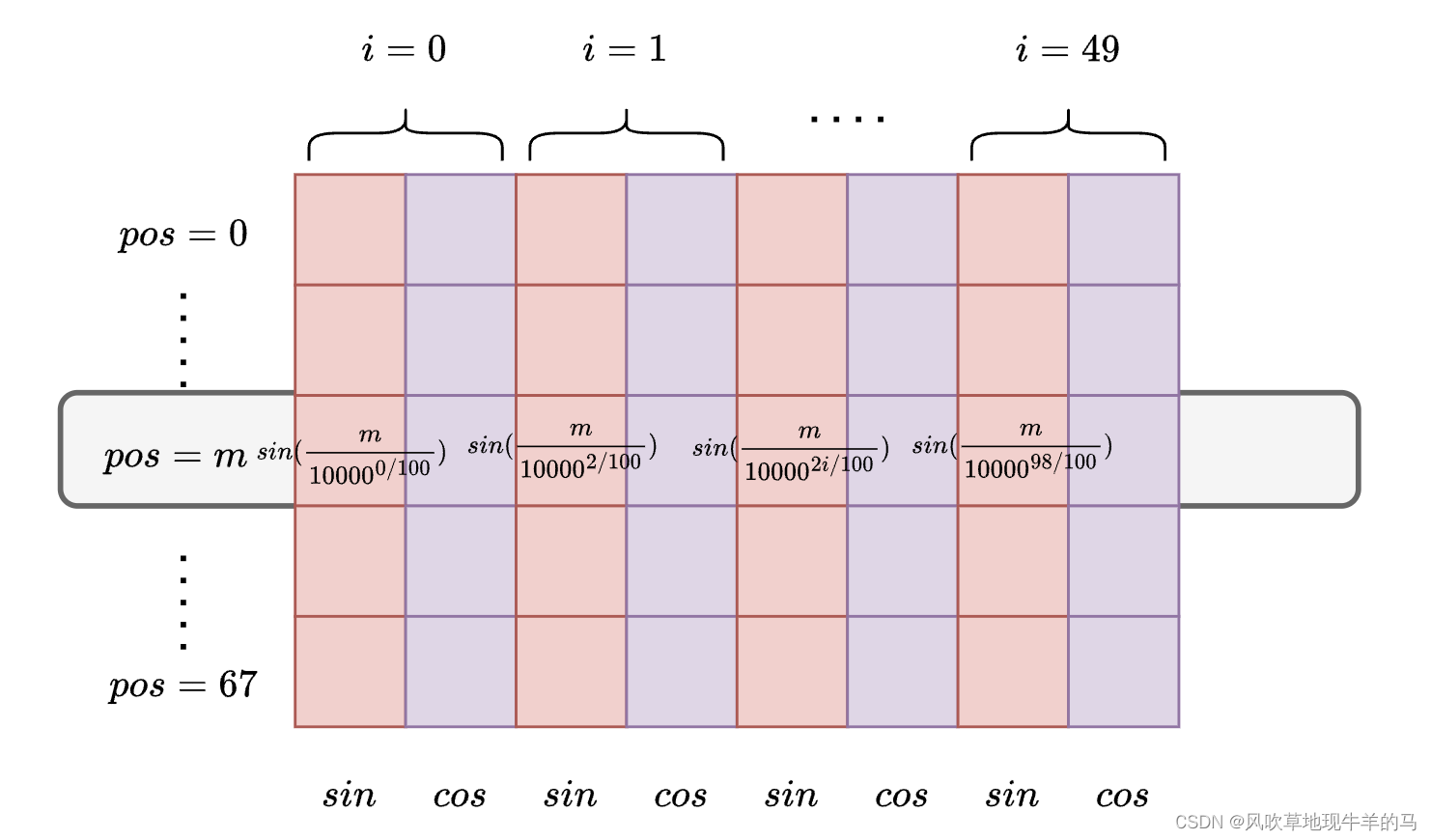
回顾正弦位置编码那一节的二维平面图，即可发现，$sin(m,\theta )$即是上图中的第$m$行中的偶数列，而$cos(m,\theta )$即是上图中的第$m$行的奇数列，所以，我们可以借助正弦位置编码那一节中的$get\_SinPositionEncoding$函数，提前获得这样的一个矩阵，然后再按需取对应的行列，组成$sin(m,\theta )$和$cos(m,\theta )$。

注意，

• 这里的上图中的$sin(m,\theta )$与公式(2)中的略有区别，公式(2)中的$sin(m,\theta )$是$d$维的，而这里的从矩阵取出的$sin(m,\theta )$是$d//2$维的。
• 回想一下，要将一个二维向量旋转，可以将其用乘以$cos(\theta )和sin(\theta )$的式子表示，这里的$cos(\theta )和sin(\theta )$记为旋转矩阵，$\theta$表示相对与基向量的旋转角度。见二维向量旋转。
  所以，对于RoPE来说，位置$m$的第$i$个分组，其旋转角度就是$m{\theta }_i$。

因此，最终attention score的计算公式也可以表达为下面的式子：
$$\begin{gathered} attentionscore=RoPE(q,m)\ast RoPE(k,n{)}^T \\ =Re[\sum _{i=0}^{d/2-1}{q}_{[2i:2i+1]}{k}_{[2i:2i+1]}^{\ast }{e}^{\mathbf{i}(m-n){\theta }_i}](3) \end{gathered}$$

在上式中，$Re$表示实部，$\mathbf{i}$表示虚数单位。公式（3）在下面还要介绍，公式（3）具有的一些周期性，对于LLM的上下文扩展具有重要的作用。

非LLaMa代码实现

公式

import torch
import torch.nn as nn


def get_SinPositionEncoding(max_sequence_length, d_model, base=10000):
    # [max_sequence_length, d_model]
    pe = torch.zeros(max_sequence_length, d_model, dtype=torch.float)

    # [0, 1, 2, ... ,d_model//2-1]   shape = [d_model//2]
    ids_x = torch.arange(d_model // 2, dtype=torch.float)  # 获得相当于x维度的ids，取值是 [0, d_model//2-1]
    exp_value = ids_x / (d_model / 2)  # 获得base的指数幂次

    alpha = 1 / (base ** exp_value)
    # 下面的这行公式同理，但是可以避免数值溢出，数学原理是：a^x = e^{x*ln(a)}
    # alpha = torch.exp(torch.arange(0, self.d_model, 2) * -(math.log(self.base) / self.d_model))

    # [0, 1, 2, ..., max_sequence_length-1]   shape = [max_sequence_length]
    pos_y = torch.arange(max_sequence_length, dtype=torch.float)

    inputs = pos_y[:, None] @ alpha[None, :]  # @表示矩阵乘法，*表示对应元素乘
    embedding_sin = torch.sin(inputs)
    embedding_cos = torch.cos(inputs)

    pe[:, 0::2] = embedding_sin  # 偶数位置设置为sin
    pe[:, 1::2] = embedding_cos  # 奇数位置设置为cos
    return pe



def RoPE(q, k):
    # q,k: (bs, head, max_len, output_dim)
    batch_size = q.shape[0]
    nums_head = q.shape[1]
    max_len = q.shape[2]
    d_model = q.shape[-1]

    # (max_len, d_model)
    pos_emb = get_SinPositionEncoding(max_len, d_model)
    # (1, 1, max_len, d_model)
    pos_emb = pos_emb.unsqueeze(0).unsqueeze(0)

    # cos_pos,sin_pos: (bs, nums_head, max_len, d_model)
    # 看rope公式可知，相邻cos，sin之间是相同的，所以复制一遍。如(1,2,3)变成(1,1,2,2,3,3)
    cos_pos = pos_emb[..., 1::2].repeat_interleave(2, dim=-1)  # 将奇数列信息抽取出来也就是cos 拿出来并复制
    sin_pos = pos_emb[..., 0::2].repeat_interleave(2, dim=-1)  # 将偶数列信息抽取出来也就是sin 拿出来并复制

    # q,k: (bs, head, max_len, d_model)
    q_inv = torch.stack([-q[..., 1::2], q[..., ::2]], dim=-1)
    q_inv = q_inv.reshape(q.shape)  # reshape后就是正负交替了

    # 更新q, *对应位置相乘
    q = q * cos_pos + q_inv * sin_pos

    k_inv = torch.stack([-k[..., 1::2], k[..., ::2]], dim=-1)
    k_inv = k_inv.reshape(k.shape)
    # 更新k, *对应位置相乘
    k = k * cos_pos + k_inv * sin_pos

    return q, k

q = torch.randn(2, 6, 13, 4)
k = torch.randn(2, 6, 13, 4)
q,k = RoPE(q, k)

LLaMA3代码实现（transformers库中的实现）

LLaMA3对于RoPE的实现，与上面的实现有所不同，但是两种方式得到的$q_{rope}与k_{rope}$的向量内积结果是一样的。

$$\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ ..\\ q_{d/2-2}\\ q_{d/2-1}\\ q_{d/2}\\ q_{d/2+1}\\ ..\\ q_{d-2}\\ q_{d-1}\end{array}\right]\ast \left[\begin{array}{c}cosm{\theta }_0\\ cosm{\theta }_1\\ cosm{\theta }_2\\ ..\\ cosm{\theta }_{d/2-2}\\ cosm{\theta }_{d/2-1}\\ cosm{\theta }_0\\ cosm{\theta }_1\\ ..\\ cosm{\theta }_{d/2-2}\\ cosm{\theta }_{d/2-1}\end{array}\right]+\left[\begin{array}{c}-q_{d/2}\\ -q_{d/2+1}\\ -q_{d/2+2}\\ ..\\ -q_{d-2}\\ -q_{d-1}\\ q_0\\ q_1\\ ..\\ q_{d/2-2}\\ q_{d/2-1}\end{array}\right]\ast \left[\begin{array}{c}sinm{\theta }_0\\ sinm{\theta }_1\\ sinm{\theta }_2\\ ..\\ sinm{\theta }_{d/2-2}\\ sinm{\theta }_{d/2-1}\\ sinm{\theta }_0\\ sinm{\theta }_1\\ ..\\ sinm{\theta }_{d/2-2}\\ sinm{\theta }_{d/2-1}\end{array}\right](4)$$
公式（1）与公式（4）有下面几点不同：

• 公式（1）中，cos和sin列是两两重复，公式（4）中，cos和sin列是拼接
• 公式（1）中，$q_{inv}$列是奇偶、负正交错，公式（4）中，是$q$后半部分为负与前半部分拼接在一起。

import torch
import torch.nn as nn

class LlamaRotaryEmbedding(nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None, scaling_factor=1.0):
        super().__init__()
        self.scaling_factor = scaling_factor
        self.dim = dim
        self.max_position_embeddings = max_position_embeddings
        self.base = base
        inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2, dtype=torch.int64).float().to(device) / self.dim))
        self.register_buffer("inv_freq", inv_freq, persistent=False)
        # For BC we register cos and sin cached
        self.max_seq_len_cached = max_position_embeddings

    @torch.no_grad()
    def forward(self, x, position_ids):
        # x: [bs, num_attention_heads, seq_len, head_size]
        # position_ids: [bs, seq_len]

        # [bs, dim//2, 1]
        inv_freq_expanded = self.inv_freq[None, :, None].float().expand(position_ids.shape[0], -1, 1)
        # [bs, 1, seq_len]
        position_ids_expanded = position_ids[:, None, :].float()
        # Force float32 since bfloat16 loses precision on long contexts
        # See https://github.com/huggingface/transformers/pull/29285
        device_type = x.device.type
        device_type = device_type if isinstance(device_type, str) and device_type != "mps" else "cpu"
        with torch.autocast(device_type=device_type, enabled=False):
            # [bs, seq_len, dim//2]
            freqs = (inv_freq_expanded.float() @ position_ids_expanded.float()).transpose(1, 2)
            # [bs, seq_len, dim]
            emb = torch.cat((freqs, freqs), dim=-1)
            cos = emb.cos()
            sin = emb.sin()
        return cos.to(dtype=x.dtype), sin.to(dtype=x.dtype)

def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)


def apply_rotary_pos_emb(q, k, cos, sin, position_ids=None, unsqueeze_dim=1):
    """Applies Rotary Position Embedding to the query and key tensors.

    Args:
        q (`torch.Tensor`): The query tensor.
        k (`torch.Tensor`): The key tensor.
        cos (`torch.Tensor`): The cosine part of the rotary embedding.
        sin (`torch.Tensor`): The sine part of the rotary embedding.
        position_ids (`torch.Tensor`, *optional*):
            Deprecated and unused.
        unsqueeze_dim (`int`, *optional*, defaults to 1):
            The 'unsqueeze_dim' argument specifies the dimension along which to unsqueeze cos[position_ids] and
            sin[position_ids] so that they can be properly broadcasted to the dimensions of q and k. For example, note
            that cos[position_ids] and sin[position_ids] have the shape [batch_size, seq_len, head_dim]. Then, if q and
            k have the shape [batch_size, heads, seq_len, head_dim], then setting unsqueeze_dim=1 makes
            cos[position_ids] and sin[position_ids] broadcastable to the shapes of q and k. Similarly, if q and k have
            the shape [batch_size, seq_len, heads, head_dim], then set unsqueeze_dim=2.
    Returns:
        `tuple(torch.Tensor)` comprising of the query and key tensors rotated using the Rotary Position Embedding.
    """
    cos = cos.unsqueeze(unsqueeze_dim)
    sin = sin.unsqueeze(unsqueeze_dim)
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed

RoPE的性质

RoPE的特性

这里需要再次回顾一下公式（3）
$$\begin{gathered} attentionscore=RoPE(q,m)\ast RoPE(k,n{)}^T \\ =Re[\sum _{i=0}^{d/2-1}{q}_{[2i:2i+1]}{k}_{[2i:2i+1]}^{\ast }{e}^{\mathbf{i}(m-n){\theta }_i}](3) \end{gathered}$$
在上式中，我们需要关注的是$e^{\mathbf{i}(m-n){\theta }_i}$，${\theta }_i=\frac{1}{bas{e}^{2i/d_{model}}}$，默认情况下，$base=10000$。
令
$$f(base,i,m-n)=e^{\mathbf{i}(m-n){\theta }_i}(5)$$
对于$f$函数来说，其可以用欧拉公式($e^{\mathbf{i}\varphi }=cos(\varphi )+\mathbf{i}sin(\varphi )$)进行变换，对于第$i$组分量来说（也就是当$i$和$base$固定时），$f$函数其实就是单位圆上的一个点，这个点会随着$m-n$在圆上转圈，如下图所示。${\theta }_i$决定了转圈的速度快慢（也就是周期）。

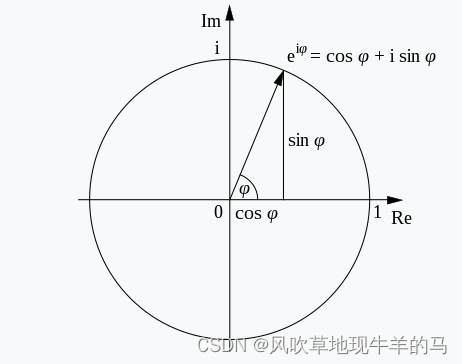
周期和频率有下面的特性:

• 当$i$固定时
  • $base\uparrow$时，${\theta }_i\downarrow$，转圈越慢、周期越长、频率越低。
  • $base\downarrow$时，${\theta }_i\uparrow$，转圈越快、周期越短、频率越高。
• 当$base$固定时
  • $i\uparrow$时，${\theta }_i\downarrow$（趋于0），转圈越慢、周期越长、频率越低。
  • $i\downarrow$时，${\theta }_i\uparrow$（趋于1），转圈越快、周期越短、频率越高。

当base固定时，我们也可以看下面的图，下面的图表示了不同的分量的变化。

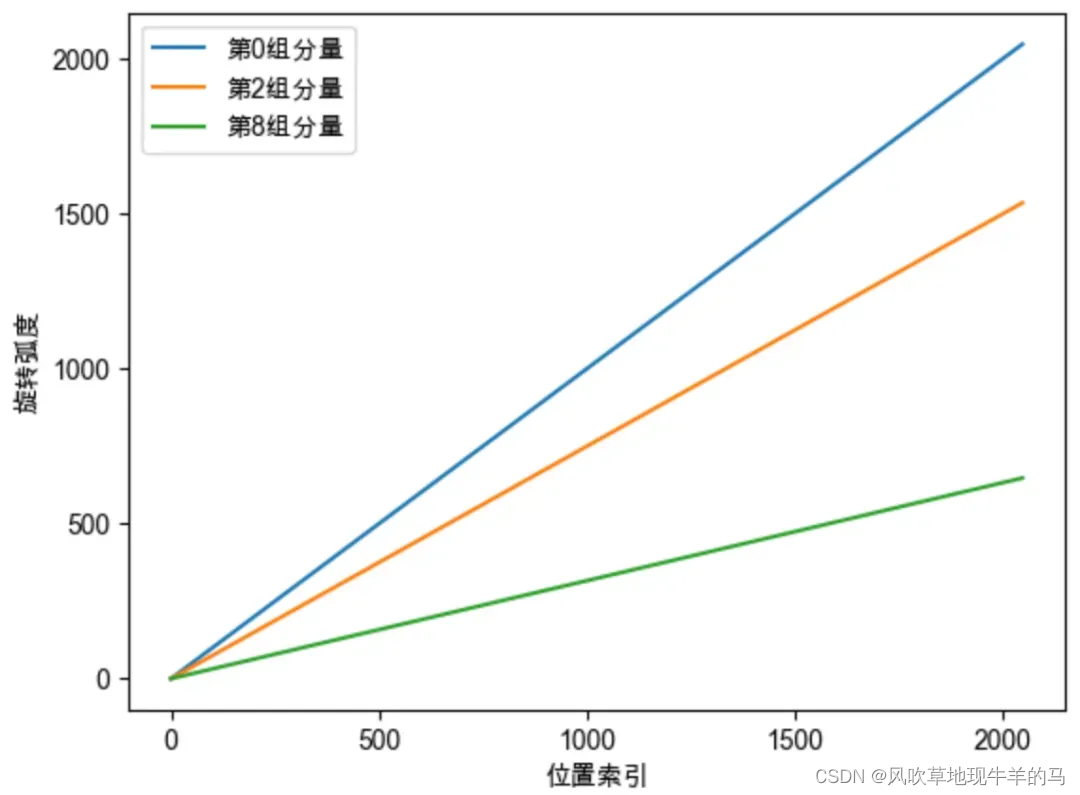
• 横坐标表示位置，纵坐标表示旋转弧度。不同的颜色，表示同一位置的不同分组的旋转弧度。
• 在rope中，位于同一位置时，越靠前的分量，旋转周期越短（高频），越靠后的分量，旋转周期越长（低频）。

位置编码外推与内插的含义

位置编码的外推与内插总结一句话：高频外推、低频内插。

那么分析了上述$f$函数的特性有什么作用呢？假设训练长度为$L_{train}$，那么$m-n\in [0,L_{train}-1]$，对于靠前的分量（$比如第0组分量$），旋转周期快、频率高，在$m-n$从$0$到$L_{t}rain-1$期间，已经转了很多圈，也就是说圈上的每一个点几乎都被训练过，因此这些${\theta }_i$几乎不存在OOD问题，可以直接进行外推；相反，对于靠后的分量（$比如第20组分量$），旋转周期慢、频率低，在$m-n$从$0$到$L_{t}rain-1$期间，可能只旋转了很小的角度，被训练过的点顶多是圆上的一段弧线，如果测试的更长的$L_{test}$，没有落在被训练过的弧度的范围内，就会出现无法预估的表现，因此需要通过内插的方法缩放到原本训练过的弧度范围内。下面的图解释了上面文本的含义。

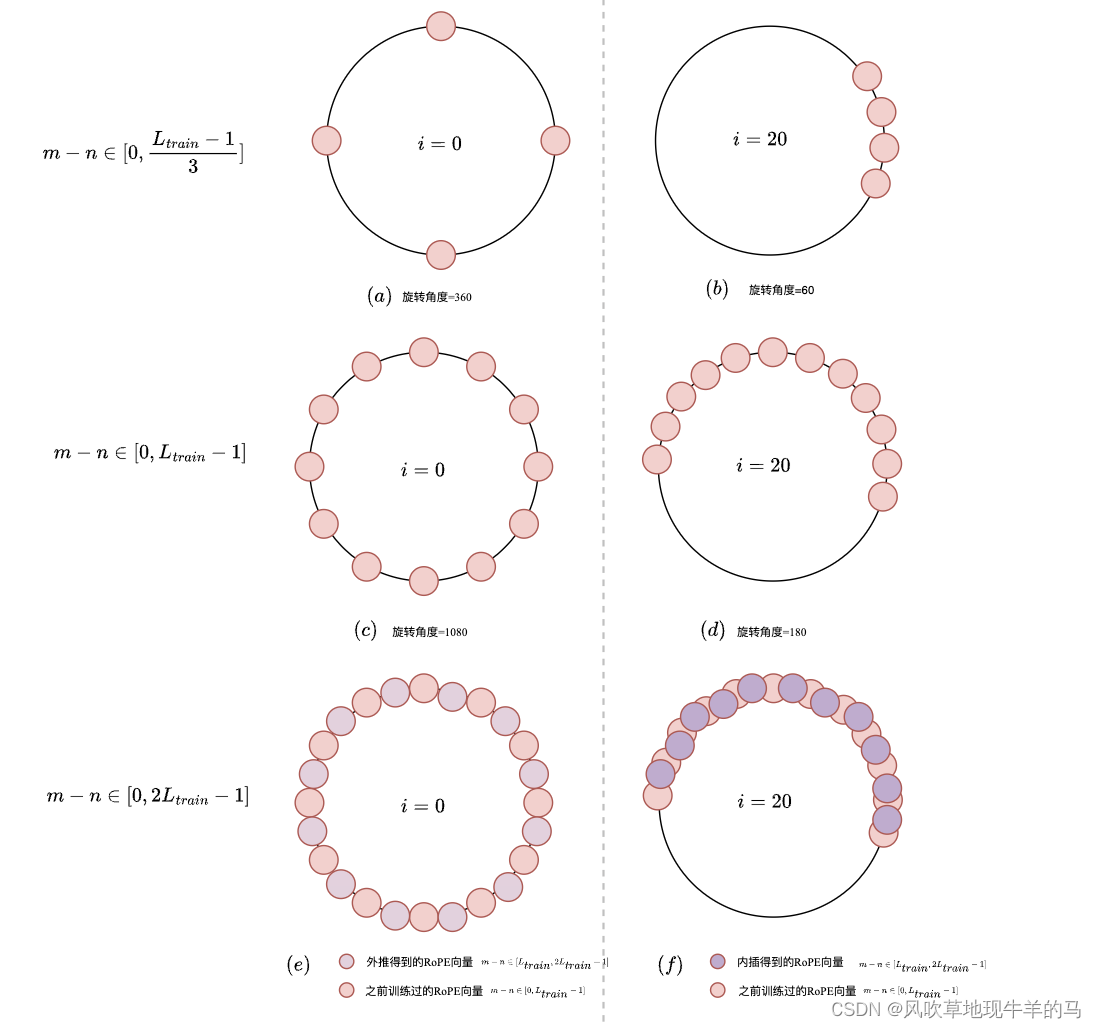
参考文献：
https://spaces.ac.cn/archives/9948
https://blog.csdn.net/v_JULY_v/article/details/134085503
https://blog.csdn.net/v_JULY_v/article/details/135072211