看完这篇文章你将会知道：
什么是并查集？
并查集的原理。
并查集的JAVA实现。
并查集这部分内容还是很简单的，相信只要认真学，你正在上小学二年级的表弟都能学得会。(´▽`ʃ♡ƪ)
目录
一、啥是并查集？
二、并查集的原理
三、并查集的JAVA实现
一、啥是并查集？
并查集是就是一个数据结构。🫡
好吧，说了等于没说。
重来，重来：
一个数据结构的出现，就对应了一个对数据操作的需求。
那么并查集要解决的需求是什么呢？
并查集主要对集合进行操作。
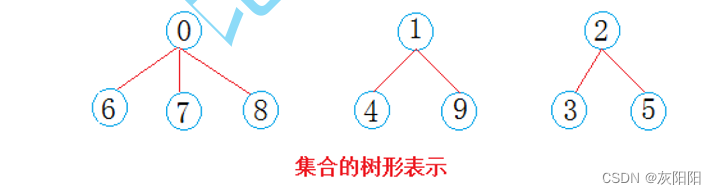
如图，假设这三个集合非常的大（树的深度与节点数很很很很很大）：
需求1：目前有一个X这个节点，我要知道，X这个节点到底是属于哪个集合的？
需求2：现在，我想把A为根节点的集合与C为根节点的集合进行合并得到一个新的集合。
需求3：目前有两个节点，分别是H和I，我想直到这两个节点是否属于同一个集合？
以上三个需求，并查集都能够实现，这也是并查集的主要功能。
二、并查集的原理
并查集的操作，刚才也看了，好神奇，但是他的原理很简单，底层就是一个1维整形数组。
那么怎样的设计能把这些集合区分开来呢？
设计规则如下：
1、数组某一个元素的下标，对应着一个集合中一个元素的编号。
2、数组某一个元素的值，要么是负整数，要么是大于等于0的整数。
3、如果数组某一个元素的值时负整数，这个元素的下标就是某一个集合的根节点编号。
这个元素的元素值（负整数）的绝对值，就是这个集合的元素个数。
4、如果数组某一个元素的值时大于等于0的整数，其元素值，是这个元素父节点的下标，
其下标就是这个元素本身在自己集合的元素编号。
空讲不好理解，下面，小编还是用一个李子来给大家介绍：
把下面这三个集合放入并查集：
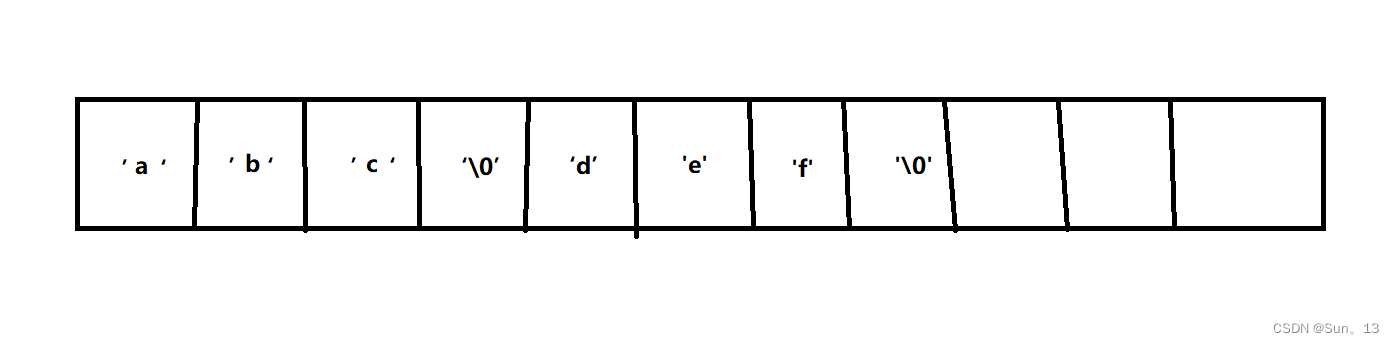
第一步，初始化数组arr（并查集）：
长度就是所有集合元素之和，每一个元素赋值-1：
现在这个数组就可以理解为有10个集合（含负数的元素个数），
每个集合的大小都是1（负数绝对值代表集合的个数）
第二步，把集合存放到并查集（具体实现文章后面讲，先看结果）：
第一次看到，这个感觉很抽象，你看，这怎么判断谁是谁的集合？
其实很简单，下面是并查集的核心理解了哦：
如果要查看下面这个5元素，是那个集合的：
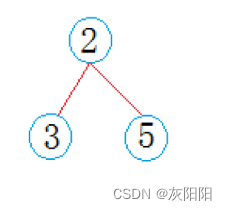那就在数组arr中找到5这个下标，5下标对应的值是2，那就跟着蓝色箭头，走到2小标对应位置。
发现arr[2]<0，那么下标2就是5这个元素所属集合的根节点编号，而arr[2]的绝对值就是集合的大小。
神奇吧。
其他的查询和上面讲的一模一样，自己可以动手试试。
三、并查集的JAVA实现
实现并查集主要就是实现一下三个目标：
1、给定一个元素，获取此元素所属集合的根节点
2、合并两个元素所属的两个集合
3、判断两个元素，是否属于同一个集合
代码：
public class UnionFindSet {
public int[] elem;//底层用数组维护
public UnionFindSet(int n) {//构造方法，设置数组长度，默认每一个元素值-1（都是一个一个的集合，只有自己一个元素）
this.elem = new int[n];
Arrays.fill(elem,-1);
}
/**
* 查找数据x 的根节点（属于那个集合）
* @param x
* @return 下标
*/
public int findRoot(int x) {
if(x < 0) {
throw new IndexOutOfBoundsException("下标不合法，是负数");
}
while (elem[x] >= 0 ) {//当值是负数时，找到集合的根结点
x = elem[x];//1 0
}
return x;
}
/**
* 查询x1 和 x2 是不是同一个集合
* @param x1
* @param x2
* @return
*/
public boolean isSameUnionFindSet(int x1,int x2) {
/**
* 获取根节点下标
* */
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2) {
return true;
}
return false;
}
/**
* 这是合并操作
* @param x1
* @param x2
*/
public void union(int x1,int x2) {//把x2合并到x1所属的集合
/**
* 获取根节点的下标
* */
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2) {//同一个元素，不需要合并
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}
public int getCount() {//获取到底有几个集合
int count = 0;
for (int x : elem) {
if(x < 0) {
count++;
}
}
return count;
}
}
