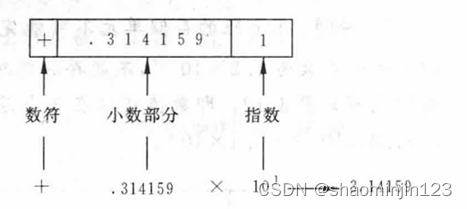
浮点数的存储形式

浮点数按照在内存中所占字节数和数值范围，可以分为浮点型，双精度浮点型和长双浮点型数。

 

 代码：

printf("lgn:%e \n", pow(exp(1), 100));
       
printf("lgn:%f ", pow(exp(1), 100));

输出结果：

exp(1)是e的一次方，pow是以e为底数，100为指数的双精度浮点型。

小数形式在C计算机中有两种形式显示

%f 小数点形式输出

%e 小数+指数形式输出

 

浮点数的运算

代码：

float pi = 3.14159261111234331;
    float x = 3.141592711113343;
    if(x > pi) printf("pi is min\n");
    if(x == pi) printf("pi is equal");
    else printf("pi is not equal!");

 输出结果：

 

浮点数的运算在计算机中其实比较复杂，拿浮点数的加法运算来讲。

第一步：对阶

加数和被加数需要先把指数调整为一致，一般通过左移或者右移来实现对阶。

第二步：尾数相加

对阶完成以后，再进行位数的有效位相加。按位与实现加法运算。

第三步：规格化

规格化是指浮点数的符号位进行取1还是取0操作，有左规和右规。具体的可以看一下组成原理，这里只是介绍一下。

fabs函数

在很多实际问题中，求值一般是近似解。如用牛顿迭代法求解方程的解，确定根的大小智能近似的满足方程。需要fabs来处理浮点数的运算。

if((fabs(x-pi) < 0.0000001)) return;

用这种方法来比较x与pi是否相等，精确范围为小数点的位数。x与pi的差的绝对值如果在0.00000001内，则认为相等，否则不相等。