二叉树的遍历(前序遍历，中序遍历，后序，层序遍历)和一些简单操作(由浅入深绝对能看懂)

欢迎大佬们的关顾能给个赞就更好啦QWQ

二叉树的逻辑结构与物理结构

一.二叉树的遍历

（1）二叉树的前序遍历

（2）二叉树的中序遍历

（3）二叉树的后序遍历

（4）二叉树的层序遍历

二.二叉树的基本操作

(1)计算二叉树的节点个数

(2)计算叶子节点的个数

(3)计算树的高度

(4)查找X值并返回节点地址

(5)返回第K层的节点个数

(6)利用前序遍历来创建树

(7)利用后序遍历来摧毁二叉树

三.层序遍历的应用判断是否为完全二叉树

其他二叉树的其他做题需要的概念与总结

四.二叉树的简单练习题

二叉树的逻辑结构与物理结构

今天来学习二叉树，当不是完全时二叉树一般用链式结构来进行表示,因为如果用数组来存储当这个树不是完全二叉树的时候将会造成大量的内存浪费。

二叉树的结构体类型如下

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

很容易想象一个二叉树的样子

由于我们的二叉树的创建将会运用到二叉树的遍历知识，所以我们优先学习二叉树的遍历，

一.二叉树的遍历

（1）二叉树的前序遍历

因为二叉树的创建也会运用到遍历和递归的思想如果你是新手建议先手搓一个二叉树出来如下图所示

	//树的创建
	BTNode* node1= CreatNode('1');
	BTNode* node2= CreatNode('2');
	BTNode* node3= CreatNode('3');
	BTNode* node4= CreatNode('4');
	BTNode* node5= CreatNode('5');
	BTNode* node6= CreatNode('6');
	BTNode* node7 = CreatNode('7');

	node1->_left = node2;
	node1->_right = node4;
	node2->_left = node3;
	node4->_left = node5;
	node4->_right = node6;
	node6->_left = node7;

前序遍历的意思就是先访问根节点再递归做子树，再递归右子树,光听肯定是很难理解的，接下来让我们看图理解,其实每一课树都要看作一个递归的过程,如果还是无法理解可以自己尝试着画一画递归展开图

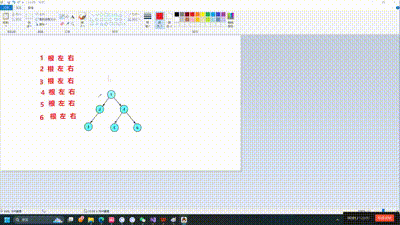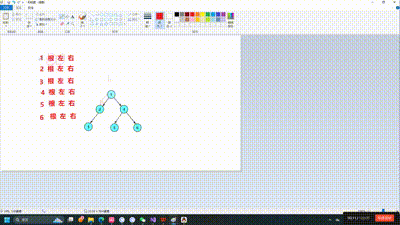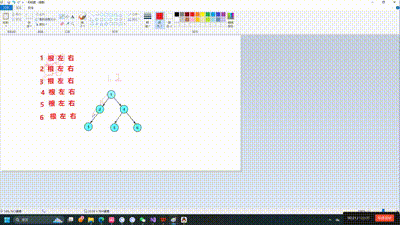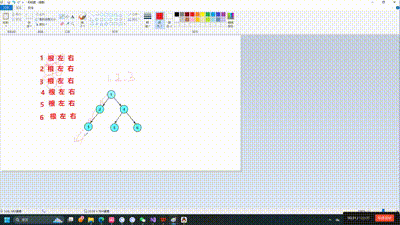
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	printf("%c ", root->_data);
	PrevOrder(root->_left);
	PrevOrder(root->_right);
}

相信通过这个动图你有了更好的理解

（2）二叉树的中序遍历

中序遍历如上一样，就是先递归左子树再访问根节点，再递归右子树

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	InOrder(root->_left);
	printf("%c ", root->_data);
	InOrder(root->_right);
}

（3）二叉树的后序遍历

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("# ");
		return;
	}
	PostOrder(root->_left);
	PostOrder(root->_right);
	printf("%c ", root->_data);
}

（4）二叉树的层序遍历

二叉树的层序遍历与递归无关但是需要有队列的知识,可以先看后面的

这里我们可以拿一支笔来一起看一下其实二叉树的层序遍历是相当于一个入队出队的过程,

出队时入队它的左右节点（不如空），直到队列为空遍历结束，你可以自己尝试画一下图，是很好理解的

void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if(root)
	QueuePush(&q,root);
	while (!QueueIsEmpty(&q))
	{
		BTNode* front= QueueGetFront(&q);
		QueuePop(&q);
		printf("%c ", front->_data);
		if (front->_left)
		QueuePush(&q, front->_left);
		if (front->_right)
		QueuePush(&q, front->_right);
	}
	QueueDestory(&q);
}

二.二叉树的基本操作

(1)计算二叉树的节点个数

当我第一次想要去实现这个函数的时候我也是想要去运用任意一个二叉树的遍历方法来进行计数，但是你会发现相当的麻烦，由于每次递归会建立栈帧，在递归中的计数全是局部变量，根本无法做到计数，除非我们在声明局部变量的时候加上static静态变量，或者使用全局变量，但是这样有会非常的不方便，由于静态变量与全局变量作用于全局这意味着每次调用这个函数前都要重新赋值为0，要不然上次的计数结果下次还会继承，使用下面就运用的递归的思路来进行解决。

int BinaryTreeSize(BTNode* root)
{
	if(root==NULL)
	return 0;
	return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

可以看见我们只需要遍历这个数，只要进入了下一个节点就会加一最后递归结束后就是二叉树的节点个数

(2)计算叶子节点的个数

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)//不是叶子节点的返回
		return 0;
	else if(root->_left==NULL&&root->_right==NULL)
	return 1;
	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

其实到了这里我们发现其实当我们想要运用递归来解决问题的时候可以先去思考函数的出口即返回的条件，所以这里可以思考什么是叶子节点，是度为0的节点，没有左右子树，当一个节点没有左右子树的时候返回一，同样遍历树的节点

(3)计算树的高度

int TreeHeigh(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftheight = TreeHeigh(root->_left);
	int rightheight = TreeHeigh(root->_right);
	//高的那边进行加一
	return leftheight > rightheight ?
		leftheight + 1: rightheight + 1;
}

一颗树的高度一般怎么来计算呢，肯定是计算高的那一边了，高的那一边进行加一，这里我们需要先进行存储左右树的高度的值，要不然将会重复调用多次，重复调用就像是大家都不记事情一样重复次数将会相当恐怖

(4)查找X值并返回节点地址

BTNode* TreeFind(BTNode* root, BTDataType x)
{
	//返回条件
	if (root == NULL)
		return NULL;
	if (root->_data == x)
		return root;
	//分解为子问题
	BTNode* temp= TreeFind(root->_left, x);
	if(temp)//由上面的返回条件可以知道，只有当这个值存在的时候才是找到，其余情况都是没有找到返回空既不存在
		return temp;
	 temp = TreeFind(root->_right, x);
	 if (temp)
		return temp;
	return NULL;
	
}

这个位置其实相当容易写错很容易就写错，比如没有return 或者一个return在前

又上面的返回条件可以知道当这个条件存在的时候就是找到了这个节点其余的返回都是空，

(5)返回第K层的节点个数

int TreeKHeighSize(BTNode* root, int k)
{
	//返回条件
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	//分解成子问题
	return TreeKHeighSize(root->_left,k-1)+ TreeKHeighSize(root->_right,k-1);
}

第K层的个数是相当于谁？其实这里可以当求第3层的节点个数时，对于第二次的根来说是求第2层

以此类推求解

(6)利用前序遍历来创建树

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)//前序遍历创建树
{
	if (a[(*pi)]=='#')
	{
		(*pi)++;
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->_data = a[(*pi)++];
	root->_left = BinaryTreeCreate(a, n, pi);
	root->_right = BinaryTreeCreate(a, n, pi);
	return root;
}

前序遍历的特点就是先访问节点，运用这个特点进行树的创建

这里我是么没有写完全的其中的n指的是二叉树的节点总个数,这里有一个易错点就是为什么要传第一个i的地址呢，其实这里就回到了很早以前学的，如何在形参里面修改实参，由于每次的调用都是会建立栈帧每次的i都是形参想要在每个函数里面的i都被实时修改那就要传递地址了就

(7)利用后序遍历来摧毁二叉树

void BinaryTreeDestory(BTNode* root)
{
	if (root==NULL)
	{
		return;
	}
	BinaryTreeDestory(root->_left);
	BinaryTreeDestory(root->_right);
	free(root);
	root = NULL;
}

三.层序遍历的应用判断是否为完全二叉树

如何判断一个树是否为而二叉树呢其实也是很简单的，当出队了一个空，就可以开始进行判断后面的节点也必须是空只要有一个不为空就说明不是完全二叉树

所以我们要对上面的层序遍历进行一下修改，空的也要进队，遇到第一个空节点开始进行判断

bool BinaryTreeComplete(BTNode* root)//1.层序遍历走,空也进队列2.遇到第一个空节点时，开始判断，后面有非空就不是完全二叉树
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	while (!QueueIsEmpty(&q))
	{
		BTNode* front = QueueGetFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			while (!QueueIsEmpty(&q))
			{
				front = QueueGetFront(&q);
				QueuePop(&q);
				if (front != NULL)//问题一内存泄漏提前返回没有进行内存释放
				{
					QueueDestory(&q);
					return false;
				}
			}
			QueueDestory(&q);
			return true;
		}
		QueuePush(&q, front->_left);
		QueuePush(&q, front->_right);
	}
	QueueDestory(&q);
	return true;
}