【数据结构|C语言版】树、二叉树和堆

前言
1. 树
- 1.1 树的概念
- 1.2 树的表示
- 1.3 树在实际中的运用
- 1.4 树的实现
2. 二叉树
- 2.1 二叉树的概念和结构
- 2.2 二叉树的性质
- 2.3 二叉树的存储结构
- 2.4 二叉树的代码实现
3. 堆
4. 二叉树顺序结构的实现
5. 二叉树链式结构的实现
结语

在这里插入图片描述

#include<GUIQU.h>
int main {
上期回顾: 【数据结构|C语言版】栈和队列
个人主页：C_GUIQU
归属专栏：【数据结构（C语言版）学习】
return 一键三连;
}

前言

各位小伙伴大家好！上次小编给大家讲解了数据结构中的栈和队列，接下来我们讲解一下树、二叉树和堆！

1. 树

1.1 树的概念

树（Tree）是一种抽象数据类型（ADT），用于模拟具有层次关系的数据集合。在树形结构中，数据以节点（Node）的形式存储，并且每个节点都可以有零个或多个子节点。以下是树相关的基本概念：

节点（Node）：树的基本单元，包含数据元素和指向其子节点的链接。
根节点（Root）：树的最顶端节点，没有父节点。
子节点（Child）：从某个节点延伸出的节点称为该节点的子节点。
父节点（Parent）：如果一个节点拥有子节点，那么这个节点称为其子节点的父节点。
叶节点（Leaf）：没有子节点的节点称为叶节点或终端节点。
兄弟节点（Sibling）：共享同一父节点的节点互称为兄弟节点。
节点的层（Level）：节点的层级从根节点开始定义，根节点为第一层，其子节点为第二层，以此类推。
树的深度（Depth）或高度（Height）：树中节点的最大层级数称为树的深度或高度。树的深度通常从1开始计数，而树的高度通常从0开始计数。
子树（Subtree）：树的任意节点及其后代节点构成的树称为该节点的子树。
路径（Path）：从一个节点到另一个节点的序列，其中包含了经过的节点和边的序列。
边（Edge）：连接两个节点的线段，表示节点之间的关系。
度（Degree）：一个节点拥有的子节点数称为该节点的度。
树的遍历（Traversal）：按照一定的顺序访问树中的所有节点。常见的遍历方法有：前序遍历（Preorder）、中序遍历（Inorder）和后序遍历（Postorder）。
查找（Search）：在树中查找一个特定的节点。
插入（Insertion）：向树中添加一个新的节点。
删除（Deletion）：从树中移除一个节点。
树的应用非常广泛，例如在数据库、文件系统、组织结构、决策树、游戏AI等领域。树的不同类型包括二叉树、二叉搜索树（BST）、平衡树（如AVL树、红黑树）、堆（Heap）、B树、Trie（前缀树）等，每种类型都有其特定的用途和特性。

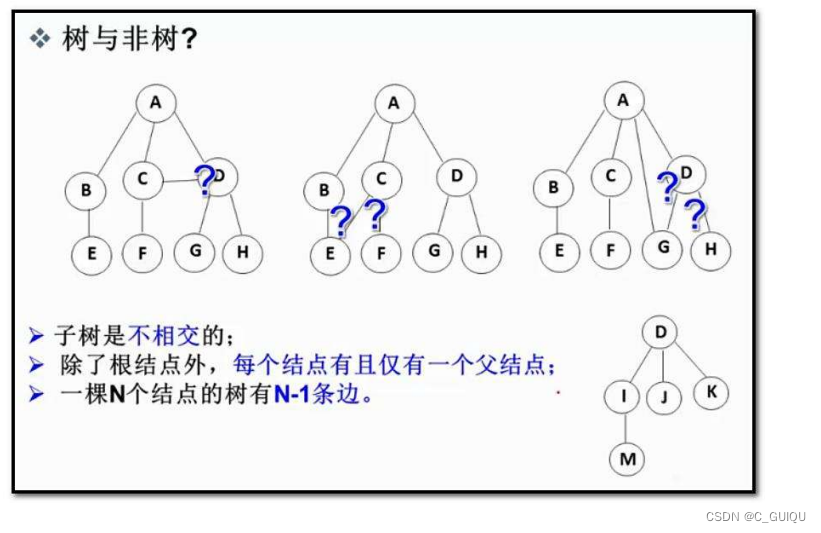
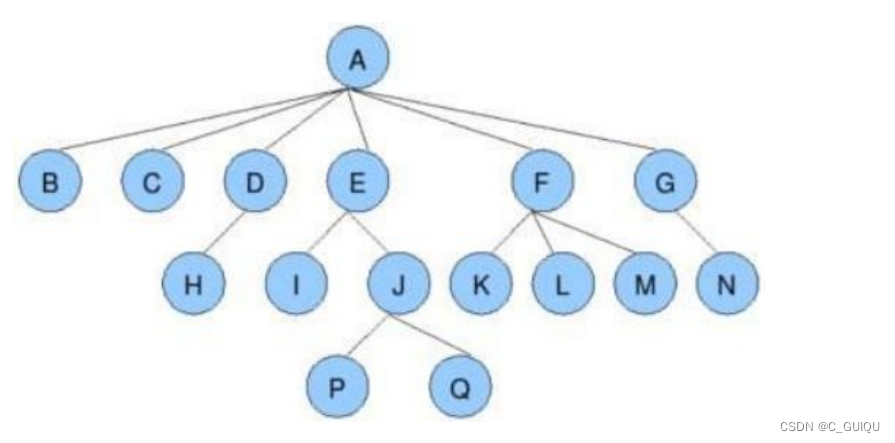
在这里插入图片描述

1.2 树的表示

树的数据结构可以用多种方式表示。以下是一些常见的树表示方法：

链接表示法：
- 节点和指针：每个节点通常由一个数据元素和多个指向其子节点的指针组成。对于二叉树，通常有两个指针，一个指向左子节点，另一个指向右子节点。
- 结构体定义：在C语言中，可以使用结构体来定义树的节点。例如，一个二叉树的节点可以定义为：
```
struct TreeNode {
    int data;
    struct TreeNode *left;
    struct TreeNode *right;
};
```
数组表示法：
- 顺序存储：对于完全二叉树或满二叉树，可以使用数组来表示。在这种表示法中，数组的第一个元素（通常索引为1）用于根节点，而节点的左子节点位于2*i的位置，右子节点位于2*i + 1的位置，其中i是节点在数组中的索引。
- 紧凑表示：这种表示方法节省空间，但不适用于非完全二叉树，因为可能会浪费数组中的空间。
嵌套集合表示法：
- 左孩子右兄弟表示法：在这种表示法中，每个节点除了指向其第一个子节点的指针外，还包含一个指向其下一个兄弟节点的指针。这种表示法适用于多叉树。
- 结构体定义：在C语言中，可以使用以下结构体来定义节点：
```
struct TreeNode {
    int data;
    struct TreeNode *firstChild;
    struct TreeNode *nextSibling;
};
```
字符串表示法：
- 括号表示法：在这种表示法中，树被表示为一个括号嵌套的字符串，其中每个节点的子树被一对括号括起来。例如，二叉树的括号表示法可以是(A(B,C))，其中A是根节点，B和C是子节点。
图形表示法：
- 可视化工具：使用图形界面工具来绘制树的形状，使得树的结构更加直观。这在教学和文档中非常常见。
  不同的表示方法有各自的优缺点，适用于不同的应用场景。在实际应用中，选择哪种表示方法取决于树的类型、操作的类型以及效率要求。例如，链接表示法在插入和删除操作上更加灵活，而数组表示法在访问特定索引的节点时更加高效。

1.3 树在实际中的运用

树在实际应用中非常广泛，它们以各种形式出现在计算机科学和日常生活的许多领域。以下是一些树的实际应用示例：

文件系统：在计算机的文件系统中，文件和目录被组织成树状结构。每个目录可以包含文件和其他目录（子目录），形成层级结构。
组织结构：公司、政府机构和其他组织的结构通常以树的形式表示，其中顶层是首席执行官或总统，下面是各个部门或机构的负责人。
决策树：在机器学习中，决策树是一种用于分类和回归的模型，它通过一系列判断来决策。
数据库索引：数据库管理系统使用B树、B+树、红黑树等数据结构来优化搜索操作，这些数据结构都是树的变体。
优先队列：堆（Heap）是一种特殊的树（通常是二叉树），用于实现优先队列，它可以快速地插入元素和删除最小（或最大）元素。
路由算法：在网络中，路由算法使用树来决定数据包从源点到目的地的最佳路径。
语法分析：在编译器的构建过程中，抽象语法树（AST）用于表示源代码的语法结构。
搜索算法：二叉搜索树（BST）用于优化搜索操作，它可以快速地插入、删除和查找数据。
游戏AI：在视频游戏中，行为树和决策树用于控制非玩家角色（NPC）的行为和决策过程。
XML/HTML解析：XML和HTML文档可以被视为树状结构，其中每个标签都是一个节点，文档对象模型（DOM）树用于在浏览器中解析和渲染网页。
家族树：在遗传学和社会研究中，家族树用于表示家族成员之间的关系和遗传信息。
自动完成：在搜索引擎和文本编辑器中，Trie（前缀树）用于实现自动完成功能，快速地提供与用户输入匹配的单词或短语。
数据压缩：Huffman树用于数据压缩算法中，它通过为常见字符分配较短的编码，为不常见字符分配较长的编码，来减少数据的存储空间。
这些只是树在实际情况中应用的一小部分例子。由于树提供了一种自然的层次结构，它们在需要组织和搜索复杂数据的应用中非常有用。

1.4 树的实现

#include <stdio.h>
#include <stdlib.h>

// 定义树节点的结构体
struct TreeNode {
    int data;
    struct TreeNode *left;
    struct TreeNode *right;
};

// 创建新节点的函数
struct TreeNode* createNode(int data) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    if (newNode == NULL) {
        printf("内存分配失败\n");
        exit(EXIT_FAILURE);
    }
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 插入节点的函数
struct TreeNode* insertNode(struct TreeNode* root, int data) {
    if (root == NULL) {
        return createNode(data);
    }
    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    }
    return root;
}

// 查找节点的函数
struct TreeNode* findNode(struct TreeNode* root, int data) {
    if (root == NULL || root->data == data) {
        return root;
    }
    if (data < root->data) {
        return findNode(root->left, data);
    } else {
        return findNode(root->right, data);
    }
}

// 删除节点的辅助函数，找到最小值节点
struct TreeNode* findMinNode(struct TreeNode* node) {
    struct TreeNode* current = node;
    while (current && current->left != NULL) {
        current = current->left;
    }
    return current;
}

// 删除节点的函数
struct TreeNode* deleteNode(struct TreeNode* root, int data) {
    if (root == NULL) {
        return root;
    }
    if (data < root->data) {
        root->left = deleteNode(root->left, data);
    } else if (data > root->data) {
        root->right = deleteNode(root->right, data);
    } else {
        // 节点找到，进行删除
        if (root->left == NULL) {
            struct TreeNode* temp = root->right;
            free(root);
            return temp;
        } else if (root->right == NULL) {
            struct TreeNode* temp = root->left;
            free(root);
            return temp;
        }
        // 节点有两个子节点
        struct TreeNode* temp = findMinNode(root->right);
        root->data = temp->data;
        root->right = deleteNode(root->right, temp->data);
    }
    return root;
}

// 前序遍历的函数
void preorderTraversal(struct TreeNode* node) {
    if (node == NULL) {
        return;
    }
    printf("%d ", node->data);
    preorderTraversal(node->left);
    preorderTraversal(node->right);
}

// 中序遍历的函数
void inorderTraversal(struct TreeNode* node) {
    if (node == NULL) {
        return;
    }
    inorderTraversal(node->left);
    printf("%d ", node->data);
    inorderTraversal(node->right);
}

// 后序遍历的函数
void postorderTraversal(struct TreeNode* node) {
    if (node == NULL) {
        return;
    }
    postorderTraversal(node->left);
    postorderTraversal(node->right);
    printf("%d ", node->data);
}

// 清理树的函数
void deleteTree(struct TreeNode* root) {
    if (root == NULL) {
        return;
    }
    deleteTree(root->left);
    deleteTree(root->right);
    free(root);
}

int main() {
    struct TreeNode* root = NULL;
    root = insertNode(root, 50);
    insertNode(root, 30);
    insertNode(root, 20);
    insertNode(root, 40);
    insertNode(root, 70);
    insertNode(root, 60);
    insertNode(root, 80);

    printf("前序遍历: ");
    preorderTraversal(root);
    printf("\n");

    printf("中序遍历: ");
    inorderTraversal(root);
    printf("\n");

    printf("后序遍历: ");
    postorderTraversal(root);
    printf("\n");

    struct TreeNode* node = findNode(root, 60);
    if (node != NULL) {
        printf("找到节点: %d\n", node->data);
    } else {
        printf("节点未找到\n");
    }

    root = deleteNode(root, 20);
    printf("删除节点 20 后的中序遍历: ");
    inorder

2. 二叉树

2.1 二叉树的概念和结构

二叉树是一种特殊的树形数据结构，每个节点最多有两个子节点，通常称为左子节点和右子节点。

以下是二叉树的一些基本概念和结构：

节点（Node）：树的基本单元，每个节点包含数据元素和指向其子节点的指针。
根节点（Root）：二叉树的最顶端节点，没有父节点。
子节点（Child）：从某个节点延伸出的节点称为该节点的子节点，在二叉树中，分为左子节点和右子节点。
父节点（Parent）：如果一个节点拥有子节点，那么这个节点称为其子节点的父节点。
叶节点（Leaf）：没有子节点的节点称为叶节点或终端节点。
兄弟节点（Sibling）：共享同一父节点的节点互称为兄弟节点。
节点的层（Level）：节点的层级从根节点开始定义，根节点为第一层，其子节点为第二层，以此类推。
深度（Depth）：节点的深度是指从根节点到该节点的唯一路径上的边的数量。
高度（Height）：节点的高度是指从该节点到最远叶节点的路径上的边的数量。整个二叉树的高度是指根节点的高度。
路径（Path）：从一个节点到另一个节点的序列，其中包含了经过的节点和边的序列。
子树（Subtree）：每个节点的左子节点和右子节点及其后代节点构成了该节点的左子树和右子树。
满二叉树（Full Binary Tree）：每个节点都有0个或2个子节点的二叉树。
完美二叉树（Perfect Binary Tree）：除了叶节点外，每个节点都有两个子节点，并且所有叶节点都在同一层的二叉树。
完全二叉树（Complete Binary Tree）：除了最后一层外，每一层都是满的，并且最后一层的节点都靠左排列。
平衡二叉树（Balanced Binary Tree）：任一节点的左右子树的高度差不超过1的二叉树。
二叉搜索树（Binary Search Tree, BST）：左子树的所有节点都小于根节点，右子树的所有节点都大于根节点的二叉树。
AVL树：任何节点的两个子树的高度最大差别为1的平衡二叉搜索树。
红黑树：一种自平衡的二叉搜索树，其中每个节点包含一个颜色作为附加信息。
二叉树的结构可以通过链接方式表示，每个节点包含数据元素和两个指向其子节点的指针。例如，在C语言中，可以使用以下结构体来定义二叉树的节点：

struct TreeNode {
    int data;              // 节点存储的数据
    struct TreeNode *left;  // 指向左子节点的指针
    struct TreeNode *right; // 指向右子节点的指针
};

通过这种方式，可以构建和操作各种类型的二叉树，如二叉搜索树、平衡树等。二叉树在计算机科学中非常重要，因为它们提供了一种高效的方式来组织和访问数据。例如，二叉搜索树可以快速地插入、删除和查找数据，而平衡二叉树如AVL树和红黑树则保证了这些操作的最坏情况时间复杂度为O(log n)。
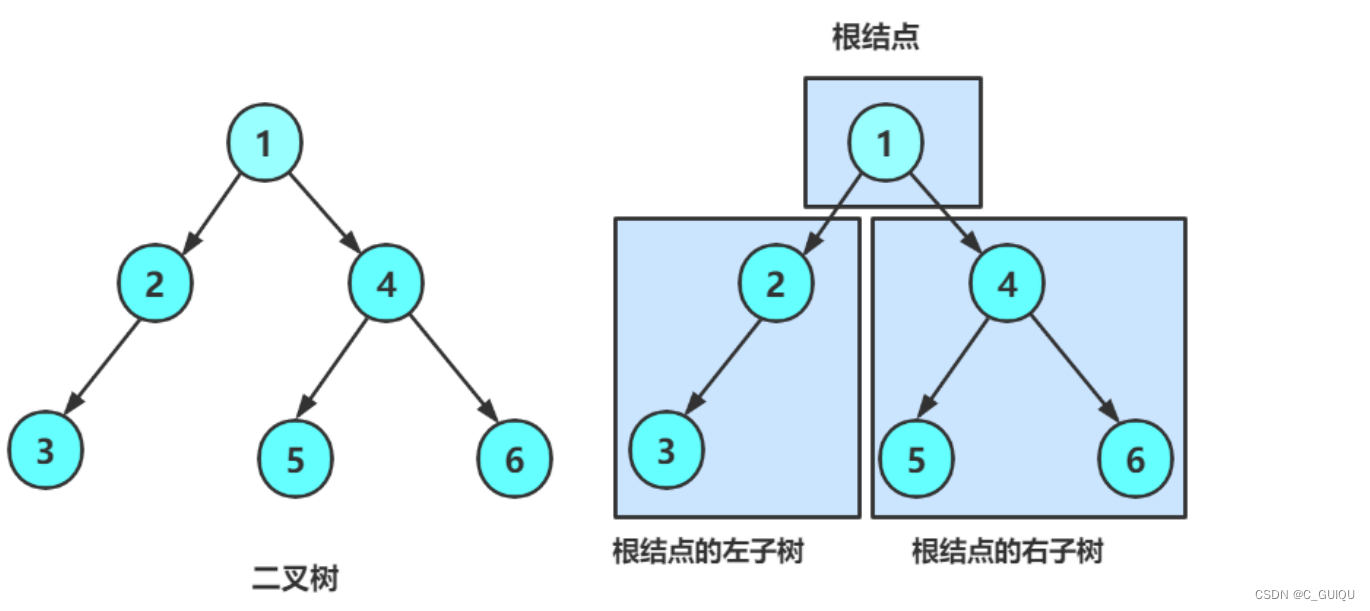
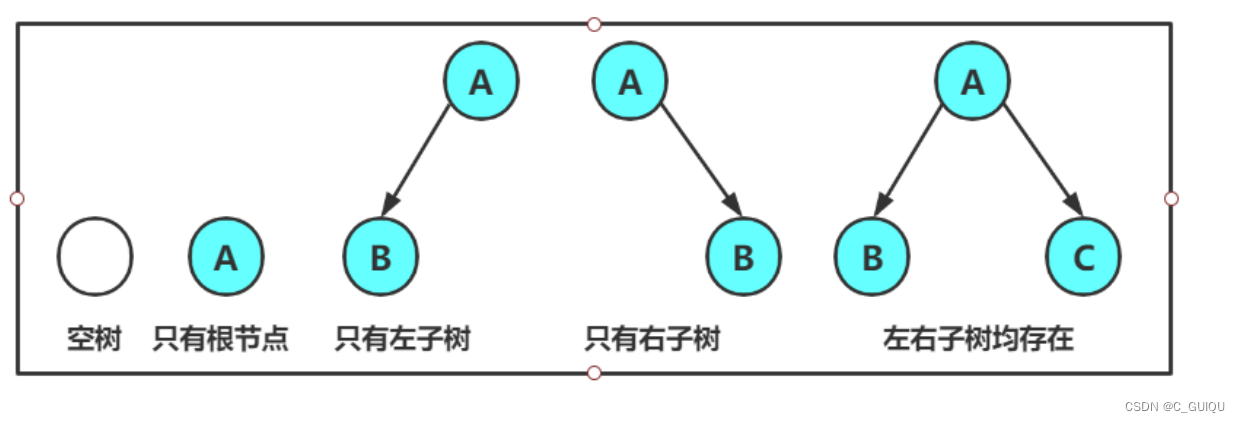
在这里插入图片描述

在这里插入图片描述

2.2 二叉树的性质

非空性质：每个二叉树至少有一个节点。
节点性质：二叉树的每个节点包含以下三个部分：
- 数据域（Data）：存储节点数据的域。
- 左指针（Left）：指向左子树的指针，如果节点没有左子树，则该指针为NULL。
- 右指针（Right）：指向右子树的指针，如果节点没有右子树，则该指针为NULL。
根节点性质：二叉树的根节点没有父节点，它的左指针和右指针都为NULL。
子节点性质：对于二叉树中的任意一个节点，其左子树和右子树也是二叉树，且左子树的根节点是该节点的左子节点，右子树的根节点是该节点的右子节点。
层次性质：二叉树中的节点可以按照层次进行编号，根节点为第1层，其子节点为第2层，依此类推。
节点度数：二叉树中每个节点的度数最多为2，即每个节点最多有两个子节点。
路径性质：从根节点到树中任意节点的路径都是唯一的。
树的高度：二叉树的高度是从根节点到最远叶节点的最长路径上的边的数量。
节点的最大深度：在二叉树中，每个节点的最大深度是该节点到其最远叶节点的路径上的边的数量。
叶节点的性质：叶节点是没有子节点的节点，也称为终端节点。
非叶节点的性质：非叶节点至少有一个子节点。
完全二叉树性质：除了最后一层外，其他所有层都是满的，最后一层的节点都靠左排列。
满二叉树性质：每个节点都有两个子节点的二叉树。
完美二叉树性质：除了叶节点外，每个节点都有两个子节点，并且所有叶节点都在同一层的二叉树。
平衡二叉树性质：二叉树中任意节点的两个子树的高度差不超过1的二叉树。
二叉搜索树性质：二叉搜索树（BST）是一种特殊的二叉树，满足左子树的所有节点值小于根节点的值，右子树的所有节点值大于根节点的值。

这些性质使得二叉树在数据结构中非常有用，因为它们提供了一种高效的方式来组织和访问数据。

2.3 二叉树的存储结构

二叉树的存储结构通常指的是如何将二叉树的数据以某种形式存储在计算机的内存中。
常见的二叉树存储结构有顺序存储结构和链式存储结构。

顺序存储结构：
- 数组：使用一维数组来存储二叉树的所有节点。在这种表示中，通常假设树是完全二叉树或接近完全二叉树，这样可以有效利用数组的连续空间。
- 紧凑表示：对于非完全二叉树，可以使用紧凑表示法，其中非叶子节点的指针指向数组中的下一个节点，而叶子节点的指针指向NULL。
链式存储结构：
- 链表：使用链表来存储二叉树的节点。每个节点包含数据域和两个指针域，分别指向其左子节点和右子节点。
- 堆栈：可以使用堆栈来模拟二叉树的后序遍历。
- 队列：可以使用队列来模拟二叉树的前序遍历和中序遍历。

顺序存储结构的优势在于随机访问节点的效率较高，但是插入和删除操作可能需要移动大量节点，导致效率较低。链式存储结构则相反，插入和删除操作的效率较高，但是随机访问节点的效率较低。
在实际应用中，选择哪种存储结构取决于具体的应用场景和对性能的要求。例如，对于需要频繁插入和删除操作的应用，链式存储结构可能更加合适；而对于需要频繁随机访问节点的应用，顺序存储结构可能更加合适。

2.4 二叉树的代码实现

以下是一个简单的C语言程序，实现了二叉树的创建、插入、查找、删除和遍历操作：

#include <stdio.h>
#include <stdlib.h>

// 定义二叉树节点的结构体
struct TreeNode {
    int data;
    struct TreeNode *left;
    struct TreeNode *right;
};

// 创建新节点的函数
struct TreeNode* createNode(int data) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    if (newNode == NULL) {
        printf("内存分配失败\n");
        exit(EXIT_FAILURE);
    }
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 插入节点的函数
struct TreeNode* insertNode(struct TreeNode* root, int data) {
    if (root == NULL) {
        return createNode(data);
    }
    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    }
    return root;
}

// 查找节点的函数
struct TreeNode* findNode(struct TreeNode* root, int data) {
    if (root == NULL || root->data == data) {
        return root;
    }
    if (data < root->data) {
        return findNode(root->left, data);
    } else {
        return findNode(root->right, data);
    }
}

// 删除节点的函数
struct TreeNode* deleteNode(struct TreeNode* root, int data) {
    if (root == NULL) {
        return root;
    }
    if (data < root->data) {
        root->left = deleteNode(root->left, data);
    } else if (data > root->data) {
        root->right = deleteNode(root->right, data);
    } else {
        // 节点找到，进行删除
        if (root->left == NULL) {
            struct TreeNode* temp = root->right;
            free(root);
            return temp;
        } else if (root->right == NULL) {
            struct TreeNode* temp = root->left;
            free(root);
            return temp;
        }
        // 节点有两个子节点
        struct TreeNode* temp = findMinNode(root->right);
        root->data = temp->data;
        root->right = deleteNode(root->right, temp->data);
    }
    return root;
}

// 找到最小值节点的辅助函数
struct TreeNode* findMinNode(struct TreeNode* node) {
    struct TreeNode* current = node;
    while (current && current->left != NULL) {
        current = current->left;
    }
    return current;
}

// 前序遍历的函数
void preorderTraversal(struct TreeNode* node) {
    if (node == NULL) {
        return;
    }
    printf("%d ", node->data);
    preorderTraversal(node->left);
    preorderTraversal(node->right);
}

// 中序遍历的函数
void inorderTraversal(struct TreeNode* node) {
    if (node == NULL) {
        return;
    }
    inorderTraversal(node->left);
    printf("%d ", node->data);
    inorderTraversal(node->right);
}

// 后序遍历的函数
void postorderTraversal(struct TreeNode* node) {
    if (node == NULL) {
        return;
    }
    postorderTraversal(node->left);
    postorderTraversal(node->right);
    printf("%d ", node->data);
}

// 清理树的函数
void deleteTree(struct TreeNode* root) {
    if (root == NULL) {
        return;
    }
    deleteTree(root->left);
    deleteTree(root->right);
    free(root);
}

int main() {
    struct TreeNode* root = NULL;
}

3. 堆

堆（Heap）是一种特别的完全二叉树，它满足两个特性：

堆是一个完全二叉树，即树中的所有层都是满的，除了最后一层，最后一层的节点从左到右排列。
对于最大堆（Max Heap）来说，每个父节点的值都大于或等于其子节点的值；对于最小堆（Min Heap）来说，每个父节点的值都小于或等于其子节点的值。

堆通常用于实现优先队列（Priority Queue），因为可以在对数时间复杂度内找到最大或最小元素，并且可以在对数时间复杂度内删除或插入元素。

堆通常使用数组来实现。对于数组中的任意位置 i 的元素，其：

左子节点的位置是 2i（如果存在）
右子节点的位置是 2i + 1（如果存在）
父节点的位置是 i / 2（向下取整）

堆的主要操作包括：

初始化（Init）：创建一个空堆。
插入（Insert）：向堆中插入一个新元素。插入时，新元素首先被放到堆的末尾，然后与其父节点比较，如果违反了堆的性质，则进行交换，直到满足堆的性质为止。
删除（Delete）：删除堆顶元素（最大或最小元素）。删除时，将堆的最后一个元素移动到堆顶，然后与子节点比较，如果违反了堆的性质，则进行交换，直到满足堆的性质为止。
提取最大值或最小值（Extract Max/Min）：返回并删除堆顶元素。这是优先队列中常用的操作。
堆排序（Heapify）：将一个无序的数组转换为堆。这是一个建立堆的过程。

下面是一个使用 C 语言实现的最大堆的简单示例：

#include <stdio.h>
#include <stdlib.h>
void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}
void heapify(int arr[], int n, int i) {
    int largest = i; // Initialize largest as root
    int left = 2 * i + 1; // left = 2*i + 1
    int right = 2 * i + 2; // right = 2*i + 2
    // If left child is larger than root
    if (left < n && arr[left] > arr[largest])
        largest = left;
    // If right child is larger than largest so far
    if (right < n && arr[right] > arr[largest])
        largest = right;
    // If largest is not root
    if (largest != i) {
        swap(&arr[i], &arr[largest]);
        // Recursively heapify the affected sub-tree
        heapify(arr, n, largest);
    }
}
// Main function to do heap sort
void heapSort(int arr[], int n) {
    // Build heap (rearrange array)
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
    // One by one extract an element from heap
    for (int i = n - 1; i >= 0; i--) {
        // Move current root to end
        swap(&arr[0], &arr[i]);
        // call max heapify on the reduced heap
        heapify(arr, i, 0);
    }
}
// A utility function to print array of size n
void printArray(int arr[], int n) {
    for (int i = 0; i < n; ++i)
        printf("%d ", arr[i]);
    printf("\n");
}
// Driver program
int main() {
    int arr[] = {12, 11, 13, 5, 6, 7};
    int n = sizeof(arr) / sizeof(arr[0]);
    heapSort(arr, n);
    printf("Sorted array is \n");
    printArray(arr, n);
}

在这个示例中，heapify 函数用于维护堆的性质，heapSort 函数用于对数组进行堆排序。堆排序是一种不稳定的比较排序算法，其时间复杂度为 O(n log n)。

4. 二叉树顺序结构的实现

在 C 语言中实现二叉树的顺序结构，我们通常使用数组来表示树。下面是一个简单的 C 语言实现，它创建了一个二叉树，并提供了插入、查找和显示节点的功能。

#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100  // 定义数组的最大容量
// 定义二叉树结构
typedef struct {
    int data[MAX_SIZE];  // 存储节点的数组
    int size;            // 树的大小
} BinaryTree;
// 初始化二叉树
void initBinaryTree(BinaryTree *tree) {
    tree->size = 0;  // 初始时树的大小为0
}
// 判断二叉树是否为空
int isEmpty(BinaryTree *tree) {
    return tree->size == 0;
}
// 在二叉树中插入节点
void insert(BinaryTree *tree, int value, int position) {
    if (position < 1 || position > MAX_SIZE) {
        printf("位置无效\n");
        return;
    }
    if (tree->size >= MAX_SIZE) {
        printf("树已满\n");
        return;
    }
    tree->size++;  // 增加树的大小
    tree->data[position] = value;  // 在指定位置插入值
}
// 获取左子节点
int leftChild(BinaryTree *tree, int position) {
    int leftPosition = 2 * position;
    if (leftPosition <= tree->size) {
        return tree->data[leftPosition];
    } else {
        return -1;  // 表示没有左子节点
    }
}
// 获取右子节点
int rightChild(BinaryTree *tree, int position) {
    int rightPosition = 2 * position + 1;
    if (rightPosition <= tree->size) {
        return tree->data[rightPosition];
    } else {
        return -1;  // 表示没有右子节点
    }
}
// 获取父节点
int parent(BinaryTree *tree, int position) {
    if (position > 1) {
        return tree->data[position / 2];
    } else {
        return -1;  // 表示没有父节点
    }
}
// 显示二叉树
void display(BinaryTree *tree) {
    for (int i = 1; i <= tree->size; i++) {
        printf("节点位置 %d: 值 %d, 左子节点 %d, 右子节点 %d\n", i, tree->data[i], leftChild(tree, i), rightChild(tree, i));
    }
}
int main() {
    BinaryTree tree;
    initBinaryTree(&tree);
    insert(&tree, 1, 1);
    insert(&tree, 2, 2);
    insert(&tree, 3, 3);
    insert(&tree, 4, 4);
    insert(&tree, 5, 5);
    display(&tree);
    return 0;
}

在这个实现中，我们定义了一个 BinaryTree 结构，其中包含一个整数数组 data 来存储树的节点，以及一个整数 size 来表示树的大小。我们提供了初始化、插入、查找和显示树的方法。这个实现假设树是一个完全二叉树，因此它适用于完全二叉树或近似完全二叉树的情况。如果树不是完全二叉树，那么数组表示法可能会导致空间浪费。

5. 二叉树链式结构的实现

二叉树的链式结构实现通常使用节点（Node）和指针（在 C 语言中是指针，在其他语言中可能是引用或其他形式的间接访问）。每个节点包含一个数据字段和两个指针字段，分别指向其左子节点和右子节点。如果某个节点没有子节点，则相应的指针字段为 NULL。

以下是一个使用 C 语言实现的二叉树链式结构的基本操作：

#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点的结构
typedef struct TreeNode {
    int data;               // 节点存储的数据
    struct TreeNode *left;  // 指向左子节点的指针
    struct TreeNode *right; // 指向右子节点的指针
} TreeNode;
// 创建新节点
TreeNode* createNode(int value) {
    TreeNode *newNode = (TreeNode*)malloc(sizeof(TreeNode));
    if (!newNode) {
        return NULL;
    }
    newNode->data = value;
    newNode->left = newNode->right = NULL;
    return newNode;
}
// 向二叉树中插入节点
void insertNode(TreeNode **root, int value) {
    if (*root == NULL) {
        *root = createNode(value);
    } else {
        TreeNode *current = *root;
        TreeNode *parent = NULL;
        while (current != NULL) {
            parent = current;
            if (value < current->data) {
                current = current->left;
            } else {
                current = current->right;
            }
        }
        if (value < parent->data) {
            parent->left = createNode(value);
        } else {
            parent->right = createNode(value);
        }
    }
}
// 中序遍历二叉树
void inorderTraversal(TreeNode *root) {
    if (root != NULL) {
        inorderTraversal(root->left);
        printf("%d ", root->data);
        inorderTraversal(root->right);
    }
}
// 主函数
int main() {
    TreeNode *root = NULL;
    
    // 插入节点
    insertNode(&root, 50);
    insertNode(&root, 30);
    insertNode(&root, 20);
    insertNode(&root, 40);
    insertNode(&root, 70);
    insertNode(&root, 60);
    insertNode(&root, 80);
    // 中序遍历二叉树
    printf("中序遍历二叉树: ");
    inorderTraversal(root);
    printf("\n");
    
    return 0;
}

在这个实现中，我们定义了一个 TreeNode 结构，它包含一个整数值 data 和两个指向 TreeNode 的指针 left 和 right。createNode 函数用于创建一个新的节点，insertNode 函数用于向树中插入一个新的节点，inorderTraversal 函数用于中序遍历树并打印节点的值。
这个基本的实现没有包含删除节点的功能，也没有进行任何形式的平衡或优化。在实际应用中，我们可能需要根据具体需求添加更多的功能，比如平衡二叉树（如 AVL 树或红黑树）、查找节点、删除节点等。