1.什么是优先级队列

队列是一种先进先出(FIFO)的数据结构，但有些情况下，操作的数据可能带有优先级，一般出队
列时，可能需要优先级高的元素先出队列，该中场景下，使用队列显然不合适，比如：在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。
在这种情况下，数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
 

2. 优先级队列模拟实现

堆实际就是在完全二叉树的基础上进行了一些调整。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

小根堆：                                                                            大根堆：

                  
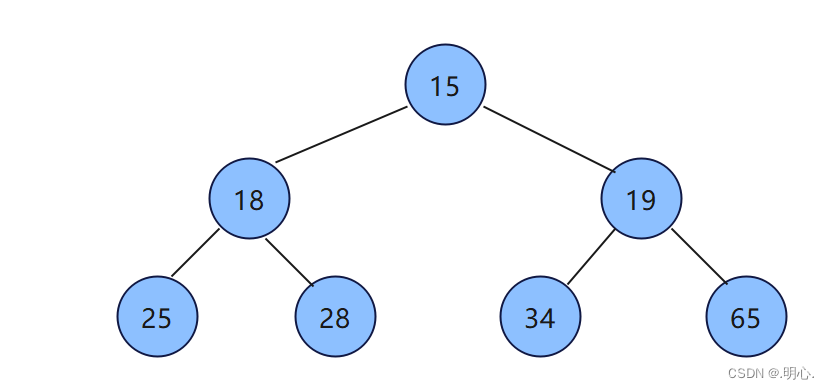
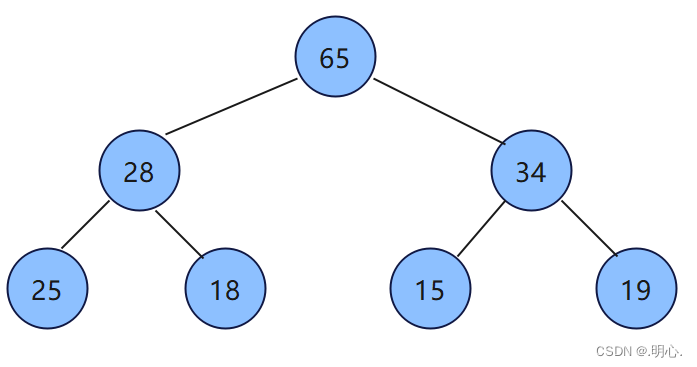
堆的性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

 

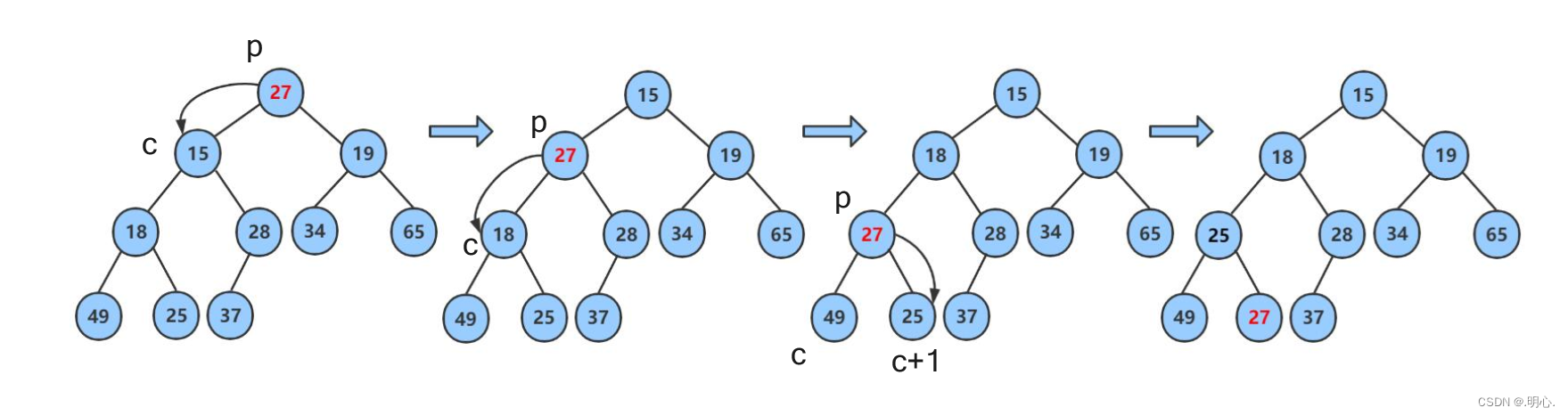
 1）堆的向下调整

 以集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据为例

1. 让parent标记需要调整的节点，child标记parent的左孩子(注意：parent如果有孩子一定先是有左孩子)

2. 如果parent的左孩子存在，即:child < end， 进行以下操作，直到parent的左孩子不存在

     ● parent右孩子是否存在，存在找到左右孩子中最小的孩子，让child进行标

     ● 将parent与较小的孩子child比较，如果：

              ◆parent小于较小的孩子child，调整结束；

              ◆否则：交换parent与较小的孩子child，交换完成之后，parent中大的元素向下移动，可能导致子树不满足堆的性质，因此需要继续向下调整，即parent = child；child = parent*2+1; 然后继续2

 

   /**
     *
     * @param parent 是每棵子树的根节点的下标
     * @param end  是每棵子树调整结束的结束条件
     * 向下调整的时间复杂度：O(logn)
     */
    private void shiftDown(int parent,int end) {
        int child=2*parent+1;
        while(child<end){
            if(child+1<usedSize && elem[child]<elem[child+1]){
                child++;
            }

            if(elem[child]>elem[parent]){
                swap(child,parent);
                parent=child;
                child=2*parent+1;
            }else {
                break;
            }
        }

    }

    private void swap(int i,int j) {
        int tmp = elem[i];
        elem[i] = elem[j];
        elem[j] = tmp;
    }

 

2）建堆 

  public void createBigHeap(int[] array) {
        for(int parent=(usedSize-1-1)/2;parent>=0;parent--){
            shiftDown(parent,usedSize);
        }
  }

 

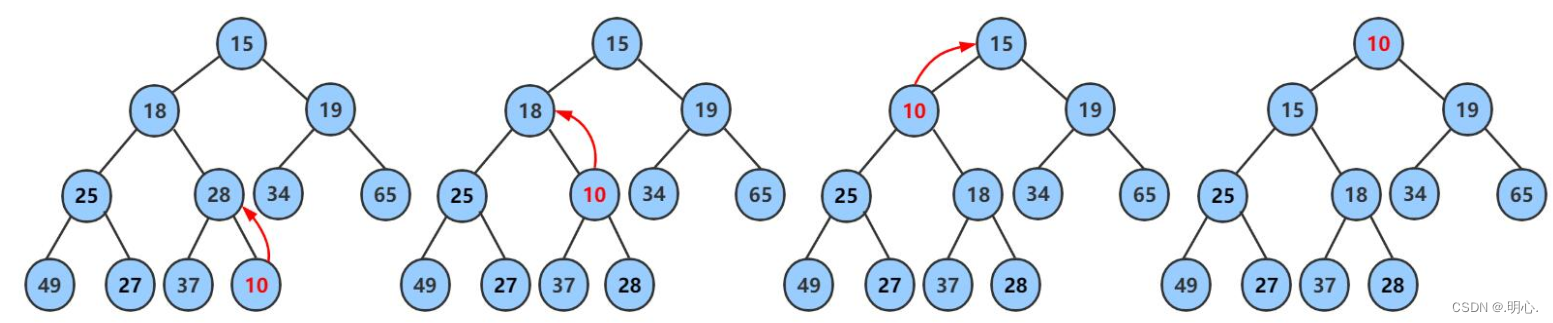
3）堆的插入

1. 先将元素放入到底层空间中(注意：空间不够时需要扩容)
2.  将最后新插入的节点向上调整，直到满足堆的性质

 

 /**
     * 堆的删除：每次删除的都是优先级高的元素
     * 仍然要保持是大根堆
     */
    public int poll() {
        if(isEmpty()){
            return -1;
        }
        int tmp=elem[0];
        swap(0,usedSize-1);
        usedSize--;
        shiftDown(0,usedSize);
        return tmp;
    }

    public boolean isEmpty() {
        return usedSize==0;
    }

 

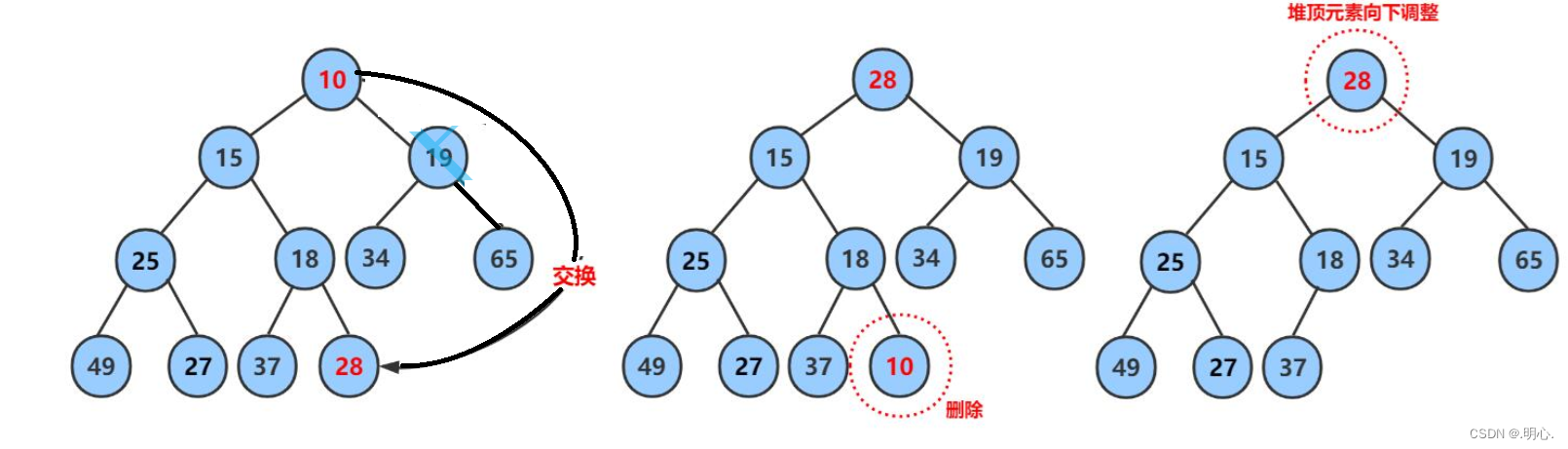
4）堆的删除

1.  将堆顶元素对堆中最后一个元素交换
2.  将堆中有效数据个数减少一个
3.  对堆顶元素进行向下调整

 

    /**
     * 堆的插入：仍然要保持是大根堆
     * @param val
     */
    public void offer(int val) {
        if(isFull()){
            this.elem= Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize]=val;
        usedSize++;

        shiftUp(usedSize-1);
    }

    private void shiftUp(int child) {
        int parent=(child-1)/2;
        while(child<0){
            if(elem[child]>elem[parent]){
                swap(child,parent);
                child=parent;
                parent=(child-1)/2;
            }else {
                break;
            }
        }
    }

 

 全部代码： 

import java.util.Arrays;

public class PriorityQueue {
    public int[] elem;
    public int usedSize;//数组已使用的空间

    public PriorityQueue() {
        this.elem=new int[10];
    }
    
    //初始化elem数组
    public void initElem(int[] array){
        for(int i=0;i<elem.length;i++){
            elem[i]=array[i];
            usedSize++;
        }
    }

    /**
     * 建堆的时间复杂度：O(N)
     *
     * @param array
     */
    public void createBigHeap(int[] array) {
        for(int parent=(usedSize-1-1)/2;parent>=0;parent--){
            shiftDown(parent,usedSize);
        }
    }

    /**
     *
     * @param parent 是每棵子树的根节点的下标
     * @param end  是每棵子树调整结束的结束条件
     * 向下调整的时间复杂度：O(logn)
     */
    private void shiftDown(int parent,int end) {
        int child=2*parent+1;
        while(child<end){
            if(child+1<usedSize && elem[child]<elem[child+1]){
                child++;
            }

            if(elem[child]>elem[parent]){
                swap(child,parent);
                parent=child;
                child=2*parent+1;
            }else {
                break;
            }
        }

    }
    private void swap(int i,int j) {
        int tmp = elem[i];
        elem[i] = elem[j];
        elem[j] = tmp;
    }


    /**
     * 堆的插入：插入完后仍然要保持是大根堆
     * @param val
     */
    public void offer(int val) {
        if(isFull()){
            this.elem= Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize]=val;
        usedSize++;

        shiftUp(usedSize-1);
    }

    private void shiftUp(int child) {
        int parent=(child-1)/2;
        while(child<0){
            if(elem[child]>elem[parent]){
                swap(child,parent);
                child=parent;
                parent=(child-1)/2;
            }else {
                break;
            }
        }
    }

    public boolean isFull() {
        return usedSize==elem.length;
    }

    /**
     * 堆的删除：每次删除的都是优先级高的元素
     * 仍然要保持是大根堆
     */
    public int poll() {
        if(isEmpty()){
            return -1;
        }
        int tmp=elem[0];
        swap(0,usedSize-1);
        usedSize--;
        shiftDown(0,usedSize);
        return tmp;
    }

    public boolean isEmpty() {
        return usedSize==0;
    }

    /**
     * 获取堆顶元素
     * @return
     */
    public int peek (){
        return elem[0];
    }
}