当大家看了鄙人的上一篇博客栈后,稍微猜一下应该知道鄙人下一篇想写的博客就是堆了吧。毕竟堆栈在C语言中常常是一起出现的。那么堆是什么,是如何实现的嘞。接下来我就带大家去尝试实现一下堆。
堆的含义
首先我们要写出一个堆,那么我们就需要要了解堆是什么。那么堆是什么嘞。堆是一种特殊的数据结构,它是一棵完全二叉树,同时满足堆属性,即父节点的值总是大于或小于其子节点的值。如果父节点的值总是大于子节点的值,那么我们称之为大根堆;反之,如果父节点的值总是小于子节点的值,那么我们称之为小根堆。在堆中,根节点的值最大(大根堆)或最小(小根堆),因此它也被称为堆顶。这个大家可以简单的理解,大根:谁大谁当爹。小根:谁小谁当爹。不知道大家是否有联想到我们一起学习的大小端问题。就是我们的内存存放。当然这里是没有关联的只是名字很像,大家应该会想到这些。
堆的定义
那么当我们了解了堆是什么之后,那么我们就来实现了。首先想堆栈既然这两个字都可以组成一个词了,那么我们实现堆可不可以用实现栈的方法来实现。所以我们首先要来定义一个结构体,来存放我们要放的东西和下标。为什么有下标嘞其实大家就理解为下一个数据的坐标嘛。毕竟堆是抽象的,不想我们数组那样用下标可以直接找,那么我们结构体只有这些嘛,我们数组建立是不是要需要确定它的起始容量,就算我们最开始不确定去起始容量,也需要确定它的数组内容。那么我们是不是需要在结构体里面确定好它的起始容量?在后续使用中,如果需要的话,我们再翻二倍开始扩容。这个应该在前面的博客中有提及过。那么我们接下来就写写结构的创建:

这其实很简单,就像我们栈一样,只需要创建结构体,然后写这些内容就可以了。
堆初始化
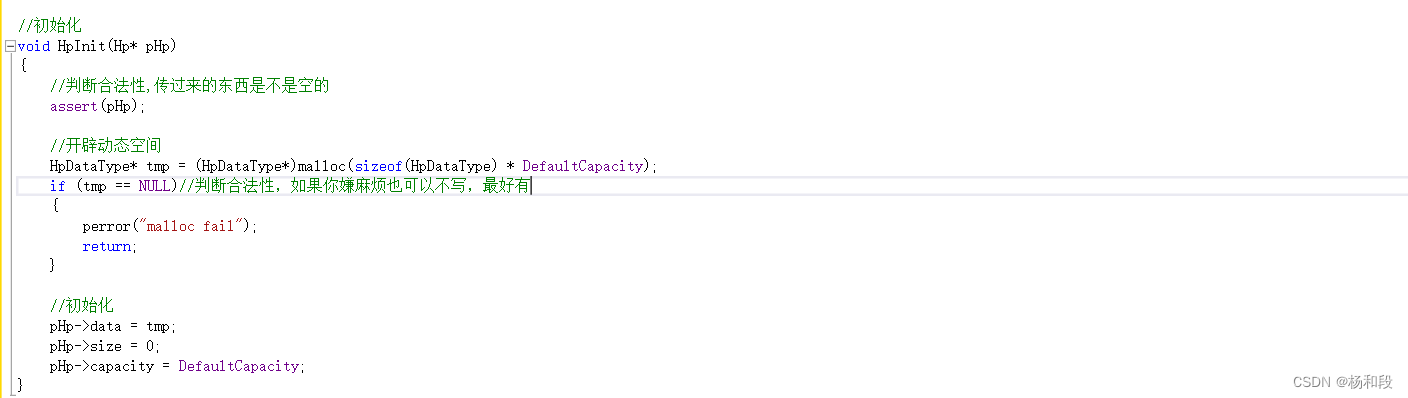
既然我已经将堆定义了,但是我们没有确定里面内容呀。那么接下来我们就将写堆的初始化。我们开始知道,不就是创建结构体嘛,所以我们需要用malloc。然后将里面的内容一一初始化,这样就结束了。
堆销毁
那么接下来我们经写了,对了,初始化了,竟然还有创建那么肯定有销毁,然后堆销毁的话其实是比较简单的,我们只需要这样申请的malloc free掉,然后将下标这些清为零就可以了。
对于栈的销毁,堆的销毁是比较简单的。只是大多数人都会在free后忘了将其置为NULL,这个是比较常见且简单的错误,希望大家都不要犯这个错误。
堆的插入
好,那我们写了将堆里面的内容初始化后,我们需要往里面插入我们想要的数据。那么我们往里面插入数据的话,一直插,一直插肯定需要判断是否版满了吧。然后接着就是判断满了之后我们需要扩容。当这些处理好之后,我们就需要将里面的数据处理。大家都知道我们在最开始上面写的就是一个完全二叉树,然后里面就是大根和小根的排列。然后我们这里就实现大根。 
这里我们并没有将向上调整写出来,因为如果写出来的话就会显示这个代码比较多,且不是很方便。
堆的向上调整
那么我们知道向上调整就需要找到该节点的父节点。那么寻找父节点的坐标是多少呢?我想我应该与大家讲过,当我们需要寻找一个节点的负极点,那么就是它的节点的下标减一除二。那么寻找他的直接点就相同是乘二加一。这个是经过验算的,大家可以是想着拿一个数组要不要来尝试,然后将它画成二叉树的样子。这样大家对于以后寻找节点的父子点都很简单了。那么当我们找到了父节点之后,我们就需要循环比较,因为我们需要将子节点向上调整。大家可以想着如果我们最后插入的数是最大的,那它是不是应该跑到第一个节点那里?所以我们需要循环来判断向上调整。我们一直判断,直到他到了最开始节点后停止。当然我们也不是只判断一路,我们还需要判断其他的合理性,如果我们只一路向上调整的话,我们需要判断他的的另外一个直接点是否符合我们大端的要求?大家可以简单的理解为我们插入一个数是在最后的,然后一直向上调整,判断是否是大于父节点,然后向上一直迭代交换。直到成为祖先节点。
堆的判空
接下来我们实现的是判断堆是否为空堆。其实这个是比较简单的,大家想一下。因为我们最开始写了堆的下标。如果都为空的话,那么下标一定为零。那么我们只需要判断对的下标是否为零,这样就结束了。
对于堆判空我们是比较简单的,与我们上一篇栈判空差不多。
堆删除
好了,那我们写了堆的判空之后,我们接下来要写堆的删除。我们都知道删除堆的数据的话,肯定就是删除堆顶的数据。那为什么是删除堆顶的数据而不是堆底的数据呢?大家想想,如果我们删除堆叠的数据的话,我们如同在一个排行榜中把数据最下面的人删除掉了。我们上次最顶的那一个数据的话,那我们我们就上一个排行榜一样,我们点排行榜一定会从上而下的看。并且这样写会更有一些价值。我们后面如果想要找到中国富豪榜前十的话,这样就很有用。对于删除的话,我们就只需要向头节点和结点交换之后将下标减一,那么我们就删除了尾节点了。我们还是老样子将比较多的代码单独拿出来写,这样看起来也会好些。

堆的向下调整
好了,那我们下来写对的上下调节。向上调节我们很简单,只需要用这个节点与父亲节点比较就可以了。但是向下调整了,我们就需要多判断一下,因为他可能会有两个孩子左右节点都有可能存在,然后需要多判断一下。那么我们判断是不是只需要判断大的那个就可以了?因为我们将左右孩子判断一下谁大?然后我们再用父亲节点与他的那个还直接判断,如果比他还大的话,那么就是没问题吧?毕竟因为我们都是写的是大端。注意:向下调整的条件是左右子树必须是堆。
堆顶数据
我们小区对定数据的话其实就很简单,就如同我们判断对是否为空一样。我们只需要先判断传过来的数据是否正确,然后向下标为零的数据传出去,那么我们就获取了堆顶数据了。
堆的数据个数
但我们写着写着忘了我们堆里面有多少个数据的时候。那我们怎么实现的?是不是也很简单,我们只需要将我们的下标返回去就可以了,因为我们是从上标零开始的。我们直接return size就可以了。
总结
堆的实现与我们的栈的实现其实差不多的,只需要稍微思考一下排列的方法,这样就可以了。对于堆稍微需要注意的就是堆的大端和小端的排序。好奇亚的几乎可以借鉴一下栈的实现方法。那么以上呢就是鄙人想与大家分享的关于堆的一些基本实现代码还有许多不足的地方,希望大家可以在评论区留言。
//初始化
void HpInit(Hp* pHp)
{
//判断合法性,传过来的东西是不是空的
assert(pHp);
//开辟动态空间
HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * DefaultCapacity);
if (tmp == NULL)//判断合法性,如果你嫌麻烦也可以不写,最好有
{
perror("malloc fail");
return;
}
//初始化
pHp->data = tmp;
pHp->size = 0;
pHp->capacity = DefaultCapacity;
}
//堆的销毁
void HpDestroy(Hp* pHp)
{
//判断合法性
assert(pHp);
//释放内存和清理
free(pHp->data);
pHp->data = NULL;
pHp->size = pHp->capacity = 0;
}
void Swap(HpDataType* p1, HpDataType* p2)
{
HpDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//向上调整建堆
void AdjustUp(HpDataType* data, int child)
{
//判断指针有效性
assert(data);
int parent = (child - 1) / 2;
while (child > 0)
{
//向上调整呢
if (data[child] > data[parent])
{
Swap(&data[child], &data[parent]);
}
else
{
break;
}
//迭代
child = parent;
parent = (child - 1) / 2;
}
}
//插入数据
void HpPush(Hp* pHp, HpDataType x)
{
//判断指针有效性
assert(pHp);
//判断容量是否满了
if (pHp->size == pHp->capacity)
{
HpDataType* tmp = (HpDataType*)realloc(pHp->data, sizeof(HpDataType) * pHp->capacity * 2);//每次扩容*2
if (tmp == NULL)//判断空间合法性
{
perror("malloc fail");
return;
}
//扩容后
pHp->data = tmp;
pHp->capacity *= 2;
}
//数据入堆
pHp->data[pHp->size] = x;
pHp->size++;
//向上调整建堆
AdjustUp(pHp->data, pHp->size - 1);
}
void AdjustDown(HpDataType* data, int size, int parent)
{
//断言检查
assert(data);
int child = parent * 2 + 1;
while (child < size)
{
//求出左右孩子较大的那个下标
if (child + 1 < size && data[child + 1] > data[child])
{
child++;
}
//父亲比孩子小就交换位置
if (data[child] > data[parent])
{
//交换
Swap(&data[child], &data[parent]);
//迭代
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HpPop(Hp* pHp)
{
//断言检查
assert(pHp);
//删除数据
Swap(&pHp->data[0], &pHp->data[pHp->size - 1]);
pHp->size--;
//向下调整建堆
AdjustDown(pHp->data, pHp->size - 1, 0);
}
//判断是否为空
bool HpEmpty(Hp* pHp)
{
assert(pHp);
return pHp->size == 0;
}
// 取堆顶的数据
HpDataType HpTop(Hp* pHp)
{
assert(pHp);
return pHp->data[0];
}
// 堆的数据个数
int HpSize(Hp* pHp)
{
assert(pHp);
return pHp->size;
}