🎩 欢迎来到技术探索的奇幻世界👨💻
📜 个人主页:@一伦明悦-CSDN博客
✍🏻 作者简介: C++软件开发、Python机器学习爱好者
🗣️ 互动与支持:💬评论 👍🏻点赞 📂收藏 👀关注+
如果文章有所帮助,欢迎留下您宝贵的评论,点赞加收藏支持我,点击关注,一起进步!
目录
前言
正文
01-基于凝聚聚类算法的二维数字嵌入上的各种凝聚聚类
02-基于K-means聚类算法对鸢尾花数据集进行聚类
03-基于光谱聚类算法在图像分割中的应用实例
04-基于硬币图像的结构化区域分层聚类演示
前言
在机器学习中,聚类算法是一类重要的无监督学习方法,用于将数据集中的样本分成具有相似特征的组或簇。本篇博客将深入探讨四种常用的聚类算法:k-均值聚类、分层聚类算法、凝聚聚类和谱聚类。通过详细的代码示例和可视化分析,我们将理解每种算法的原理、优缺点以及适用场景。通过本文的阅读,读者将能够更好地选择并理解如何应用适合自己数据集的聚类算法,从而更有效地进行数据分析和挖掘。
正文
01-基于凝聚聚类算法的二维数字嵌入上的各种凝聚聚类
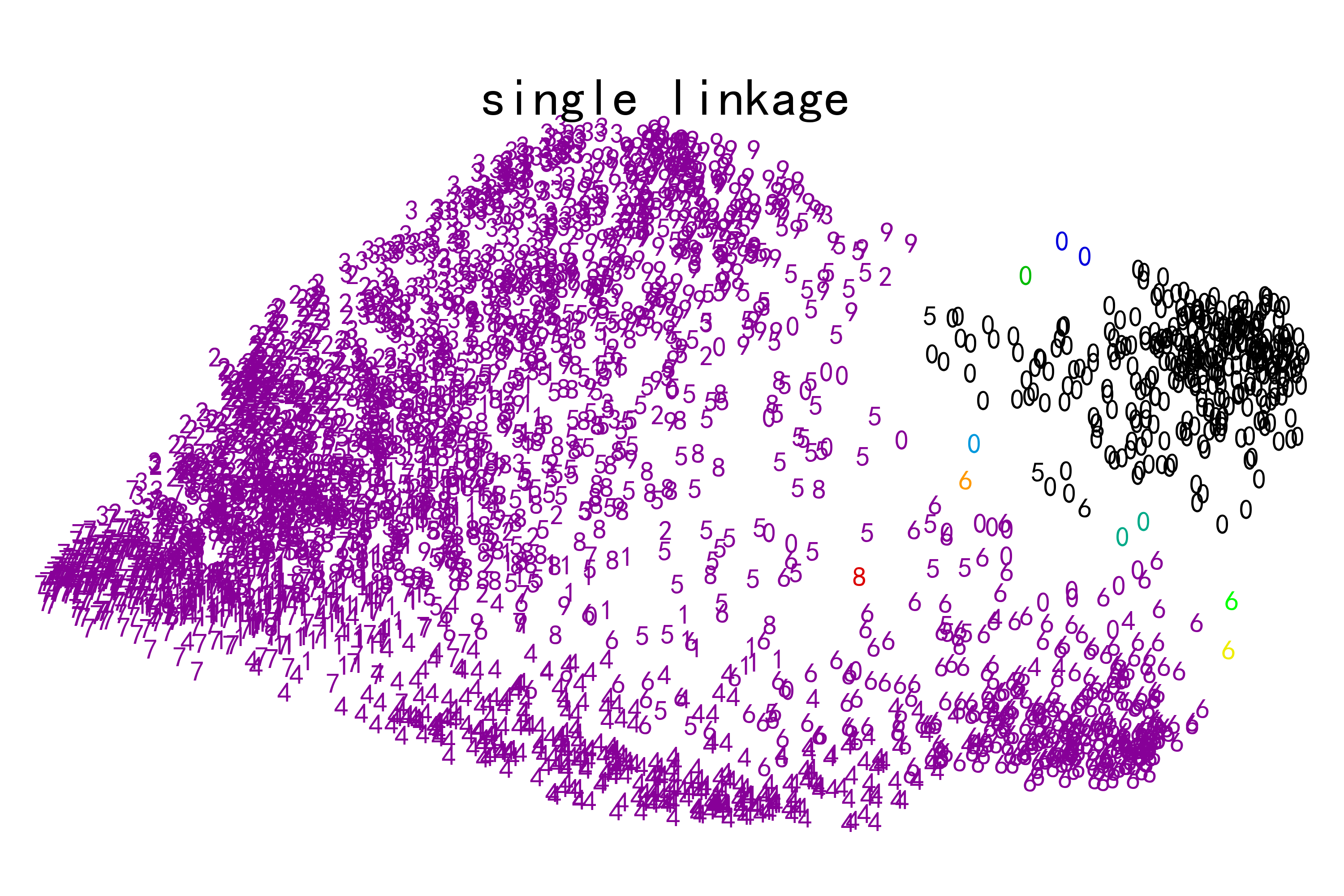
这个例子向我们展示的是聚集性聚类的“rich getting richer”的行为,这种行为往往会造成不均匀的聚类大小。这种行为对于平均链接策略来说是非常明显的,它最终产生了几个单点簇,而在单个链接中,我们得到了一个单一的中心簇,所有其他的簇都是从边缘的噪声点中提取出来的。
下面是具体代码:这段代码展示了如何使用层次聚类(Hierarchical Clustering)方法对手写数字数据集(digits dataset)进行聚类,并将不同链接方式(linkage methods)的聚类结果可视化。
导入必要的库:time:用于计算代码运行时间。numpy:用于数值计算。scipy.ndimage:用于图像处理。matplotlib.pyplot:用于绘图。sklearn.manifold:用于降维。sklearn.datasets:用于加载数据集。sklearn.cluster.AgglomerativeClustering:用于进行层次聚类。
加载数据集:使用datasets.load_digits()加载手写数字数据集,返回特征矩阵X和标签y。
定义nudge_images函数:该函数用于微调图像,以增加数据集的多样性。对每张图像进行微小的平移操作。
定义plot_clustering函数:用于绘制聚类结果的散点图。将降维后的数据X_red映射到二维空间,并根据聚类标签labels给不同类别的点上色。
降维:使用manifold.SpectralEmbedding对数据进行降维,减少特征维度到2维,以便可视化。
循环遍历不同的链接方式:对于每一种链接方式(ward、average、complete、single):将图像保存为.png文件。 调用plot_clustering函数绘制聚类结果的散点图。记录聚类运行时间。使用AgglomerativeClustering进行层次聚类,指定聚类数量为10。
from time import time
import numpy as np
from scipy import ndimage
from matplotlib import pyplot as plt
from sklearn import manifold, datasets
from sklearn.cluster import AgglomerativeClustering
X, y = datasets.load_digits(return_X_y=True)
n_samples, n_features = X.shape
np.random.seed(0)
def nudge_images(X, y):
shift = lambda x: ndimage.shift(x.reshape((8, 8)),
.3 * np.random.normal(size=2),
mode='constant').ravel()
X = np.concatenate([X, np.apply_along_axis(shift, 1, X)])
Y = np.concatenate([y, y], axis=0)
return X, Y
X, y = nudge_images(X, y)
def plot_clustering(X_red, labels, title=None):
x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
X_red = (X_red - x_min) / (x_max - x_min)
plt.figure(figsize=(6, 4))
for i in range(X_red.shape[0]):
plt.text(X_red[i, 0], X_red[i, 1], str(y[i]),
color=plt.cm.nipy_spectral(labels[i] / 10.),
fontdict={'weight': 'bold', 'size': 9})
plt.xticks([])
plt.yticks([])
if title is not None:
plt.title(title, size=17)
plt.axis('off')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
print("Computing embedding")
X_red = manifold.SpectralEmbedding(n_components=2).fit_transform(X)
print("Done.")
for linkage in ('ward', 'average', 'complete', 'single'):
clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
t0 = time()
clustering.fit(X_red)
print("%s :\t%.2fs" % (linkage, time() - t0))
plot_clustering(X_red, clustering.labels_, "%s linkage" % linkage)
plt.savefig("../%s.png" % linkage, dpi=500)
plt.show()实例运行结果如下图所示:
每张图像展示了手写数字数据集的聚类结果,颜色代表不同的聚类簇。
横坐标和纵坐标代表降维后的特征空间,点的位置表示样本在这个特征空间的投影。
每个点的标签是对应样本的真实数字标签,以帮助理解聚类效果。



02-基于K-means聚类算法对鸢尾花数据集进行聚类
图中首先显示了使用一个K-means算法产生三个聚类会是什么样的结果。然后显示错误初始化对分类过程的影响。通过将n_init设置为1(默认值为10),可以减少算法使用不同的质心种子运行的次数。下一幅图显示了使用八个聚类所能提供的信息,并最终得出了基本事实。
这段代码的作用是使用K均值聚类算法对鸢尾花数据集进行聚类,并通过可视化展示聚类结果。它可以帮助理解K均值聚类算法如何将数据点分成不同的聚类,并与实际数据集进行比较,从而评估聚类的效果。
导入库:numpy:用于数值操作。matplotlib.pyplot:用于绘图。mpl_toolkits.mplot3d 中的 Axes3D:用于3D投影。sklearn.cluster 中的 KMeans:用于K均值聚类。sklearn 中的 datasets:用于加载鸢尾花数据集。
设置随机种子:确保随机操作的可重现性。
加载鸢尾花数据集:加载鸢尾花数据集。
定义估计器:定义了三个K均值聚类估计器,具有不同的参数:k_means_iris_8:8个聚类的K均值聚类。k_means_iris_3:3个聚类的K均值聚类。k_means_iris_bad_init:3个聚类的K均值聚类,使用了糟糕的初始化策略。
设置图形编号和标题:初始化变量 fignum 和 titles 以跟踪图形和它们的标题。
绘制聚类并保存图像:对于每个估计器,创建一个3D散点图。每个数据点根据其聚类分配进行着色。将绘图保存为图像。递增图形编号。
绘制地面真相:创建另一个3D散点图以可视化地面真相。每个类别都有标签(Setosa,Versicolour,Virginica)。将绘图保存为图像。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # Required for 3D projection
from sklearn.cluster import KMeans
from sklearn import datasets
np.random.seed(5)
iris = datasets.load_iris()
X = iris.data
y = iris.target
estimators = [('k_means_iris_8', KMeans(n_clusters=8)),
('k_means_iris_3', KMeans(n_clusters=3)),
('k_means_iris_bad_init', KMeans(n_clusters=3, n_init=1,
init='random'))]
fignum = 1
titles = ['8 clusters', '3 clusters', '3 clusters, bad initialization']
# Save each figure individually
for name, est in estimators:
fig = plt.figure(fignum, figsize=(4, 3))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
est.fit(X)
labels = est.labels_
ax.scatter(X[:, 3], X[:, 0], X[:, 2],
c=labels.astype(np.float), edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title(titles[fignum - 1])
ax.dist = 12
plt.savefig("..figure_{}.png".format(fignum), dpi=500) # Save each figure
fignum += 1
# Plot the ground truth
fig = plt.figure(fignum, figsize=(4, 3))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
for name, label in [('Setosa', 0),
('Versicolour', 1),
('Virginica', 2)]:
ax.text3D(X[y == label, 3].mean(),
X[y == label, 0].mean(),
X[y == label, 2].mean() + 2, name,
horizontalalignment='center',
bbox=dict(alpha=.2, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y, edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
ax.set_title('Ground Truth')
ax.dist = 12
plt.savefig("..ground_truth.png", dpi=500) # Save the ground truth figure
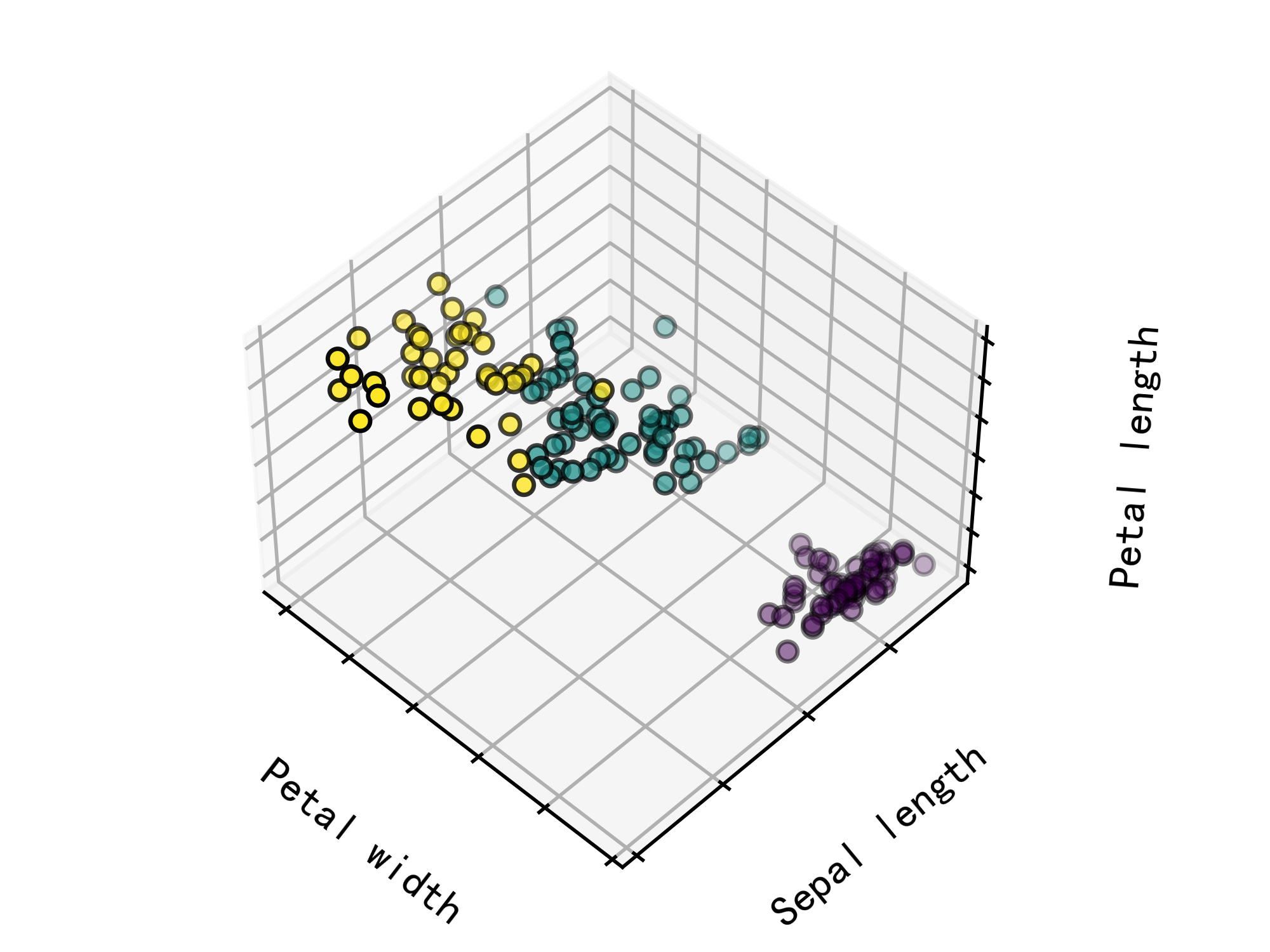
plt.show()实例运行结果如下图所示:这些可视化帮助理解K均值聚类算法如何将鸢尾花数据集分成不同的聚类,并将其与实际地面真相进行比较。
8个聚类:展示了使用K均值聚类算法将数据点划分为8个聚类。
3个聚类(良好初始化):用K均值聚类算法将数据点分组为3个聚类。
3个聚类(糟糕初始化):使用糟糕的初始化策略,将数据点聚类为3个聚类。
地面真相:表示鸢尾花数据集的实际分布,其中每个类别(Setosa,Versicolour,Virginica)以不同的颜色显示。



03-基于光谱聚类算法在图像分割中的应用实例
下面我们使用对象的掩码将图形限制在对象的轮廓上。在本例中,我们感兴趣的是将对象从一个对象和另一个对象中分离出来,而不是从背景中分离出来。这段代码演示了如何使用谱聚类(spectral clustering)算法对人工生成的图像进行分割。具体步骤如下:
生成图像:首先生成一个100x100的二维数组,表示一个图像。在图像中心生成了4个圆形区域,模拟了不同的物体或区域。
创建掩模:将生成的图像转换为布尔型掩模,以限制谱聚类算法只在感兴趣的前景区域内进行分割,而不关心背景。
添加噪声:为了使问题更贴近实际,给图像添加了一些随机噪声。
构建图:将图像转换为图形结构,其中每个像素作为图的一个节点,相邻像素之间的连接表示图的边。连接的权重由像素之间的梯度值决定。
谱聚类:对构建的图应用谱聚类算法,将图像分成指定数量的聚类。这里分别尝试了将图像分成4个和2个聚类。
可视化:使用matplotlib库将原始图像和分割后的图像进行可视化,其中分割后的图像中不同的颜色代表不同的聚类。
这段代码展示了谱聚类算法在图像分割中的应用,通过谱聚类,可以有效地将图像分割成不同的区域或对象。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_extraction import image
from sklearn.cluster import spectral_clustering
l = 100
x, y = np.indices((l, l))
center1 = (28, 24)
center2 = (40, 50)
center3 = (67, 58)
center4 = (24, 70)
radius1, radius2, radius3, radius4 = 16, 14, 15, 14
circle1 = (x - center1[0]) ** 2 + (y - center1[1]) ** 2 < radius1 ** 2
circle2 = (x - center2[0]) ** 2 + (y - center2[1]) ** 2 < radius2 ** 2
circle3 = (x - center3[0]) ** 2 + (y - center3[1]) ** 2 < radius3 ** 2
circle4 = (x - center4[0]) ** 2 + (y - center4[1]) ** 2 < radius4 ** 2
# #############################################################################
# 4 circles
img = circle1 + circle2 + circle3 + circle4
mask = img.astype(bool)
img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)
graph = image.img_to_graph(img, mask=mask)
graph.data = np.exp(-graph.data / graph.data.std())
labels = spectral_clustering(graph, n_clusters=4, eigen_solver='arpack')
label_im = np.full(mask.shape, -1.)
label_im[mask] = labels
plt.matshow(img)
plt.matshow(label_im)
plt.savefig("/segmentation_4.png", dpi=500) # Save the first segmentation figure
plt.show()
# #############################################################################
# 2 circles
img = circle1 + circle2
mask = img.astype(bool)
img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)
graph = image.img_to_graph(img, mask=mask)
graph.data = np.exp(-graph.data / graph.data.std())
labels = spectral_clustering(graph, n_clusters=2, eigen_solver='arpack')
label_im = np.full(mask.shape, -1.)
label_im[mask] = labels
plt.matshow(img)
plt.matshow(label_im)
plt.savefig("/segmentation_2.png", dpi=500) # Save the second segmentation figure
plt.show()实例运行结果如下图所示:这段代码生成了一个人工图像,其中包含了四个圆形区域,每个圆形区域具有不同的中心点和半径。以下是对生成的图像的解释:
四个圆形区域:第一个圆:中心点为 (28, 24),半径为 16。第二个圆:中心点为 (40, 50),半径为 14。第三个圆:中心点为 (67, 58),半径为 15。第四个圆:中心点为 (24, 70),半径为 14。
图像表示:图像大小为 100x100 像素。每个像素通过其与圆心的距离来确定是否属于圆形区域。每个像素被分配一个值,表示其是否属于一个或多个圆形区域。
噪声添加:对图像进行了一定程度的噪声添加,使得图像不是完美的几何形状。
掩模:图像转换为掩模,以限制聚类算法只在感兴趣的前景区域进行分割。
这个生成的图像用于模拟具有不同形状和大小的物体或区域,并作为谱聚类算法的输入,以展示算法对不同区域进行分割的效果。


04-基于硬币图像的结构化区域分层聚类演示
下面给出代码基于区域层次聚类的二维图像分割计算。聚类在空间上受到约束,以使每个分割区域成为一体。
数据生成和预处理:原始硬币图像被缩小到原始大小的20%,以加快处理速度。应用高斯滤波器对图像进行平滑处理,减少缩小时的锯齿状伪影。
数据转换:将处理后的图像转换为一维数组(X),以便进行后续聚类操作。
定义数据结构:利用grid_to_graph函数定义数据的结构,即像素与其邻域像素的连接关系。
执行聚类:利用凝聚式聚类算法(Agglomerative Clustering),将像素分成27个区域(n_clusters = 27)。采用ward链接方式进行聚类,并利用定义的数据结构(connectivity)约束聚类过程。
绘制结果:在一个新的图像上显示处理后的硬币图像,并用不同的颜色轮廓标识出不同区域的聚类结果。
代码首先将原始硬币图像进行预处理,然后将其转换为一维数组以进行聚类。
接着定义了数据结构以确保聚类在像素之间的连通性。
聚类过程采用凝聚式聚类,通过ward链接方式和数据结构进行约束。
最后,代码绘制了处理后的图像,并用不同颜色的轮廓显示出聚类的区域。
import time as time
import numpy as np
from distutils.version import LooseVersion
from scipy.ndimage.filters import gaussian_filter
import matplotlib.pyplot as plt
import skimage
from skimage.data import coins
from skimage.transform import rescale
from sklearn.feature_extraction.image import grid_to_graph
from sklearn.cluster import AgglomerativeClustering
# these were introduced in skimage-0.14
if LooseVersion(skimage.__version__) >= '0.14':
rescale_params = {'anti_aliasing': False, 'multichannel': False}
else:
rescale_params = {}
# #############################################################################
# Generate data
orig_coins = coins()
# Resize it to 20% of the original size to speed up the processing
# Applying a Gaussian filter for smoothing prior to down-scaling
# reduces aliasing artifacts.
smoothened_coins = gaussian_filter(orig_coins, sigma=2)
rescaled_coins = rescale(smoothened_coins, 0.2, mode="reflect",
**rescale_params)
X = np.reshape(rescaled_coins, (-1, 1))
# #############################################################################
# Define the structure A of the data. Pixels connected to their neighbors.
connectivity = grid_to_graph(*rescaled_coins.shape)
# #############################################################################
# Compute clustering
print("Compute structured hierarchical clustering...")
st = time.time()
n_clusters = 27 # number of regions
ward = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward',
connectivity=connectivity)
ward.fit(X)
label = np.reshape(ward.labels_, rescaled_coins.shape)
print("Elapsed time: ", time.time() - st)
print("Number of pixels: ", label.size)
print("Number of clusters: ", np.unique(label).size)
# #############################################################################
# Plot the results on an image
plt.figure(figsize=(5, 5))
plt.imshow(rescaled_coins, cmap=plt.cm.gray)
for l in range(n_clusters):
plt.contour(label == l,
colors=[plt.cm.nipy_spectral(l / float(n_clusters)), ])
plt.xticks(())
plt.yticks(())
plt.savefig("/2.png", dpi=500)
plt.show()实例运行结果如下图所示:这段代码对硬币图像进行了聚类分割,将图像分成了27个不同的区域。每个区域代表图像中相似的像素集合,这些像素在视觉上具有相似的特征。聚类过程利用了硬币图像的像素之间的连通性,确保了相邻像素在同一区域中。最后,通过在图像上绘制不同颜色的轮廓来可视化这些区域,使得每个区域的边界清晰可见。