「网络流浅谈」最大流的应用

news2024/11/24 17:38:36

更好的阅读体验

二分图匹配

考虑如何将二分图匹配问题，转化为流网络。设置 1 1 1 个汇点和源点，从源点向二分图一侧的每一个点连边，从另一侧向汇点连边，边权均为 1 1 1，二分图中的边也全部加入，权值设为 1 1 1。这样，二分图的最大匹配等于流网络的最大流。

P2756 飞行员配对方案问题

题意：给定 1 1 1 个二分图，求最大匹配。

匈牙利算法是可以求二分图最大匹配的，不过太慢了。不妨，使用上述的方式建立出流网络，并使用 Dinic 求解出该网络的最大流即可。

举个例子：左图为样例的二分图，而右图为建立的流网络。

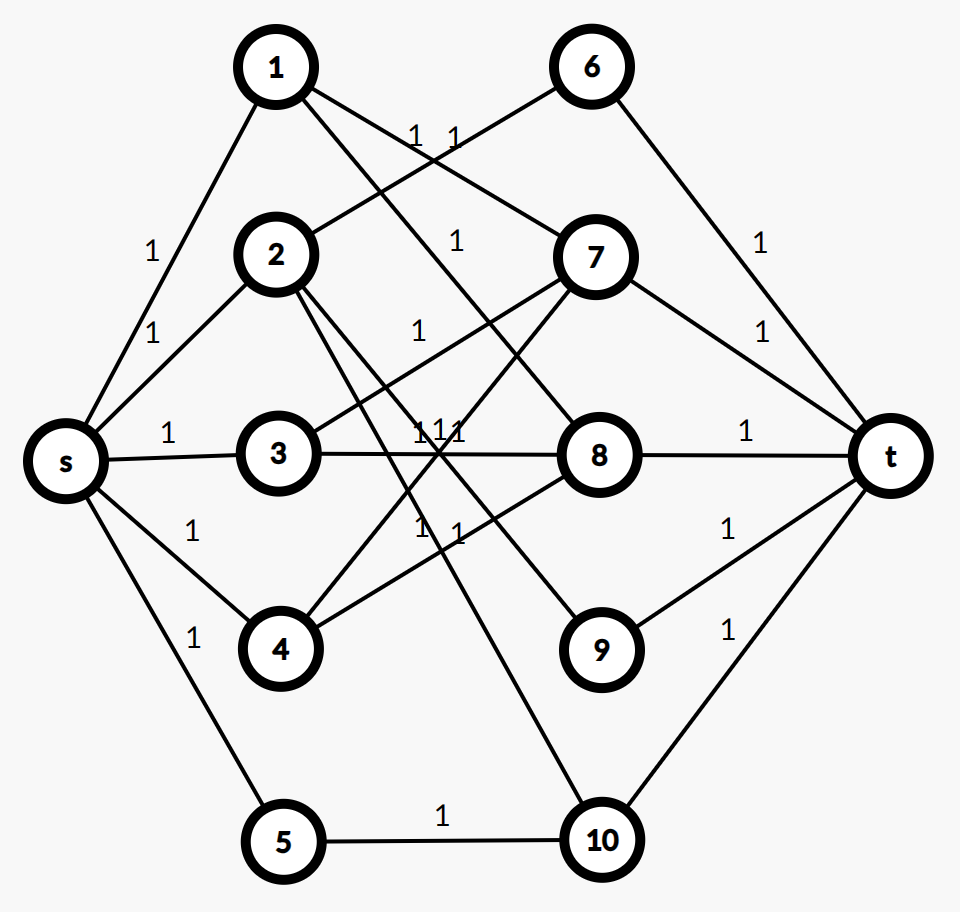
浅析流网络最大流与二分图最大匹配的相等性：

对于网络流的题目，只需要考虑对于任意的一个最大匹配，都能对应到一个可行流；而对于任意一个可行流都能对应到一个最大匹配。

对于任意的一个最大匹配，都能对应到一个可行流：若选择边 E 1 , E 2 , … , E k E_1,E_2, \dots ,E_k E1​,E2​,…,Ek​，则可行流中的这些边均为 1 1 1，且令这些边左端的顶点分别为 V 1 , V 2 , … , V t V_1,V_2,\dots,V_t V1​,V2​,…,Vt​，右端的为 V 1 ′ , V 2 ′ , … , V t ′ V'_1,V'_2,\dots, V'_t V1′​,V2′​,…,Vt′​，则可行流的 s → V i s\rightarrow V_i s→Vi​ 这些边均为 1 1 1； V i ′ → t V'_i\rightarrow t Vi′​→t 这些边也均为 1 1 1。由于匹配不存在 2 2 2 条边有公共顶点，所以一定满足容量限制与流量守恒。

对于任意的一个可行流，都能对应到一个最大匹配：可行流中流量为 1 1 1 的没有 s s s 和 t t t 的边即为最大匹配，由于流量守恒，最多有 1 1 1 条边流向一个点，所以满足对于任意 2 2 2 条边，都不存在公共点。

故，只需要用 Dinic 跑一遍最大流即可，输出方案就是找出所有反向边流量为 1 1 1（或正向边流量为 0 0 0）的边即可。

注意：二分图下的 Dinic 算法极为特殊，时间复杂度为 O ( n 2 n ) O(n^2\sqrt n) O(n2n ​)

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 1e2 + 10, M = 1e5 + 10;

int n, m, s, t;
int h[N], e[M], ne[M], f[M], idx;
int d[N], cur[N];

void add(int a, int b, int c) {
	e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx ++;
	e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx ++;
}
bool bfs() {
	memset(d, -1, sizeof d);
	queue<int> q;
	q.emplace(s), cur[s] = h[s], d[s] = 0;
	while (q.size()) {
		auto u = q.front();
		q.pop();

		for (int i = h[u]; ~i; i = ne[i]) {
			int j = e[i];
			if (d[j] == -1 && f[i]) {
				d[j] = d[u] + 1, cur[j] = h[j];
				if (j == t) return 1;
				q.emplace(j);
			}
		}
	}
	return 0;
}
int find(int u, int lim) {
	if (u == t) return lim;

	int flow = 0;
	for (int i = cur[u]; ~i && flow < lim; i = ne[i]) {
		int j = e[i];
		if (d[j] == d[u] + 1 && f[i]) {
			int tmp = find(j, min(lim - flow, f[i]));
			if (!tmp) d[j] = -1;
			f[i] -= tmp, f[i ^ 1] += tmp, flow += tmp;
		}
	}
	return flow;
}
int dinic() {
	int res = 0, flow;
	while (bfs()) while (flow = find(s, 1e18)) res += flow;
	return res;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	memset(h, -1, sizeof h);

	cin >> m >> n;

	s = 0, t = n + 1;
	int u, v;
	while (cin >> u >> v && u != -1) {
		add(u, v, 1);
	}
	for (int i = 1; i <= m; i ++)
		add(s, i, 1);
	for (int i = m + 1; i <= n; i ++)
		add(i, t, 1);

	cout << dinic() << endl;
	for (int i = 0; i < idx; i += 2)
		if (e[i] != t && e[i ^ 1] != s && !f[i])
			cout << e[i ^ 1] << " " << e[i] << endl;

	return 0;
}
习题

P3254 圆桌问题，与原建图方式有略微差异。

参考代码 
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 5e2 + 10, M = 1e5 + 10;

int m, n, s, t;
int a[N], b[N];
int h[N], e[M], f[M], ne[M], idx;
int d[N], cur[N];

void add(int a, int b, int c) {
	e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx ++;
	e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx ++;
}
bool bfs() {
	memset(d, -1, sizeof d);
	queue<int> q;
	q.emplace(s), d[s] = 0, cur[s] = h[s];
	while (q.size()) {
		int u = q.front();
		q.pop();

		for (int i = h[u]; ~i; i = ne[i]) {
			int j = e[i];
			if (d[j] == -1 && f[i]) {
				d[j] = d[u] + 1;
				cur[j] = h[j];
				if (j == t) return 1;
				q.emplace(j);
			}
		}
	}
	return 0;
}
int find(int u, int lim) {
	if (u == t) return lim;

	int flow = 0;
	for (int i = cur[u]; ~i && flow < lim; i = ne[i]) {
		cur[u] = i;
		int j = e[i];
		if (d[j] == d[u] + 1 && f[i]) {
			int tmp = find(j, min(lim - flow, f[i]));
			if (!tmp) d[j] = -1;
			f[i] -= tmp, f[i ^ 1] += tmp, flow += tmp;
		}
	}

	return flow;
}
int dinic() {
	int res = 0, flow;
	while (bfs()) while (flow = find(s, 1e18)) res += flow;
	return res;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	memset(h, -1, sizeof h);
	cin >> m >> n;

	s = 0, t = n + m + 1;
	int tot = 0;
	for (int i = 1; i <= m; i ++)
		cin >> a[i], add(s, i, a[i]), tot += a[i];
	for (int i = 1; i <= n; i ++)
		cin >> b[i], add(i + m, t, b[i]);
	for (int i = 1; i <= m; i ++)
		for (int j = m + 1; j <= n + m; j ++)
			add(i, j, 1);

	if (dinic() == tot) {
		cout << 1 << endl;
		std::vector<vector<int>> way(m + 1);
		for (int i = 0; i < idx; i += 2)
			if (e[i] != t && e[i ^ 1] != s && !f[i])
				way[e[i ^ 1]].emplace_back(e[i] - m);
		for (int i = 1; i <= m; i ++) {
			for (auto v : way[i])
				cout << v << " ";
			cout << endl;
		}
	} else {
		cout << 0 << endl;
	}

	return 0;
}

多源汇最大流

本质上只不过是源点不是 1 1 1 个，汇点也不是 1 1 1 个了，那么其实只需要再设一个超级源点连向所有源点，边权为 + ∞ +\infty +∞，表示向这些源点可以流任意多流量，也就是说从这些源点可以流出任意多流量；同样的，从每一个汇点向超级汇点连一条 + ∞ +\infty +∞ 的边，表示这些汇点可以流向超级汇点任意多流量，也就是说这些汇点都可以接纳任意多的流量。

这样的新流网络的最大流就是源网络的最大流，所以只需要对于新网络跑一遍 Dinic 即可。

习题

AcWing 2234. 多源汇最大流，模版题

参考代码 
#include <iostream>
#include <cstring>
#include <queue>
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 5e5 + 10;

int N, M, Sc, Tc, S, T;
int h[SIZE], e[SIZE], ne[SIZE], f[SIZE], idx;
int D[SIZE], Current[SIZE];

void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx ++;
    e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx ++;
}

bool BFS() {
    memset(D, -1, sizeof D);
    queue<int> Q;

    Q.push(S), D[S] = 0, Current[S] = h[S];
    while (Q.size()) {
        int u = Q.front();
        Q.pop();

        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (D[j] == -1 && f[i]) {
                D[j] = D[u] + 1;
                Current[j] = h[j];
                if (j == T) return true;
                Q.push(j);
            }
        }
    }

    return false;
}

int Find(int u, int limit) {
    if (u == T) return limit;

    int flow = 0;
    for (int i = Current[u]; ~i && flow < limit; i = ne[i]) {
        Current[u] = i;
        int j = e[i];
        if (D[j] == D[u] + 1 && f[i]) {
            int T = Find(j, min(f[i], limit - flow));
            if (!T) D[j] = -1;
            f[i] -= T, f[i ^ 1] += T, flow += T;
        }
    }

    return flow;
}

int Dinic() {
    int Result = 0, flow;
    while (BFS()) while (flow = Find(S, 1e18)) Result += flow;
    return Result;
}

signed main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    memset(h, -1, sizeof h);

    cin >> N >> M >> Sc >> Tc;

    S = 0, T = N + 1;
    while (Sc --) {
        int u;
        cin >> u;
        add(S, u, 1e18);
    }

    while (Tc --) {
        int u;
        cin >> u;
        add(u, T, 1e18);
    }

    while (M --) {
        int a, b, c;

        cin >> a >> b >> c;

        add(a, b, c);
    }

    cout << Dinic() << endl;

    return 0;
}

关键边

POJ3204 Ikki’s Story I - Road Reconstruction

题意：给定 1 1 1 个流网络，求有多少条边，满足增加该边边权后能使最大流增加。

考虑一条边满足什么条件使得增加容量后会使得最大流增加，回顾求最大流的过程：每一次在残留网络中找增广路径，并加到最大流中。

那么，如果容量增加后，最大流增加，那么必然是增加流量后产生 1 1 1 条增广路径。所以，对于每一条边 ( u , v ) (u,v) (u,v)，只需要判断是否存在 1 1 1 条增广路径 s → u s\rightarrow u s→u 以及 1 1 1 增广路径 v → t v\rightarrow t v→t。判断的方法就是在最大流的残留网络中 DFS，记录每次走 > 0 >0 >0 的边能到达那些点即可。

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 5e2 + 10, M = 2e4 + 10;

int n, m, s, t;
int h[N], e[M], ne[M], f[M], idx;
int d[N], cur[N], vis[2][N];

void add(int a, int b, int c) {
	e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx ++;
	e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx ++;
}
bool bfs() {
	memset(d, -1, sizeof d);
	queue<int> q;
	q.emplace(s), d[s] = 0, cur[s] = h[s];

	while (q.size()) {
		int u = q.front();
		q.pop();

		for (int i = h[u]; ~i; i = ne[i]) {
			int j = e[i];
			if (d[j] == -1 && f[i]) {
				d[j] = d[u] + 1, cur[j] = h[j];
				if (j == t) return 1;
				q.emplace(j);
			}
		}
	}
	return 0;
}
int find(int u, int lim) {
	if (u == t) return lim;

	int flow = 0;
	for (int i = cur[u]; ~i && flow < lim; i = ne[i]) {
		cur[u] = i;
		int j = e[i];
		if (d[j] == d[u] + 1 && f[i]) {
			int tmp = find(j, min(lim - flow, f[i]));
			if (!tmp) d[j] = -1;
			f[i] -= tmp, f[i ^ 1] += tmp, flow += tmp;
		}
	}

	return flow;
}
int dinic() {
	int res = 0, flow;
	while (bfs()) while (flow = find(s, 1e18)) res += flow;
	return res;
}
void dfs(int u, int k) {
	vis[k][u] = 1;
	for (int i = h[u]; ~i; i = ne[i]) {
		int j = e[i];
		if (!vis[k][j] && f[i ^ k])
			dfs(j, k);
	}
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	memset(h, -1, sizeof h);
	cin >> n >> m;

	s = 0, t = n - 1;
	while (m --) {
		int u, v, w;
		cin >> u >> v >> w;
		add(u, v, w);
	}
	dinic();
	dfs(s, 0), dfs(t, 1);

	int res = 0;
	for (int i = 0; i < idx; i += 2)
		if (vis[0][e[i ^ 1]] && vis[1][e[i]])
			res ++;

	cout << res << endl;

	return 0;
}

拆点

POJ3281 Dining

题意：有 n n n 头奶牛， F F F 个食物和 D D D 个饮料，每头奶牛可以吃某些食物和饮料，但都只能吃食物和饮料各一个。求最多能满足多少头奶牛。（三分图匹配）

考虑继续使用类似二分图的建网络流的方式，举个例子：

不过，这样真的能够求出最终的答案吗？答案是否定的。

考虑局部的这样一个位置，最大流得到话会流出 2 2 2 的，也就是这个奶牛会贡献 2 2 2，而应该是 1 1 1。

所以，就要拆点了！

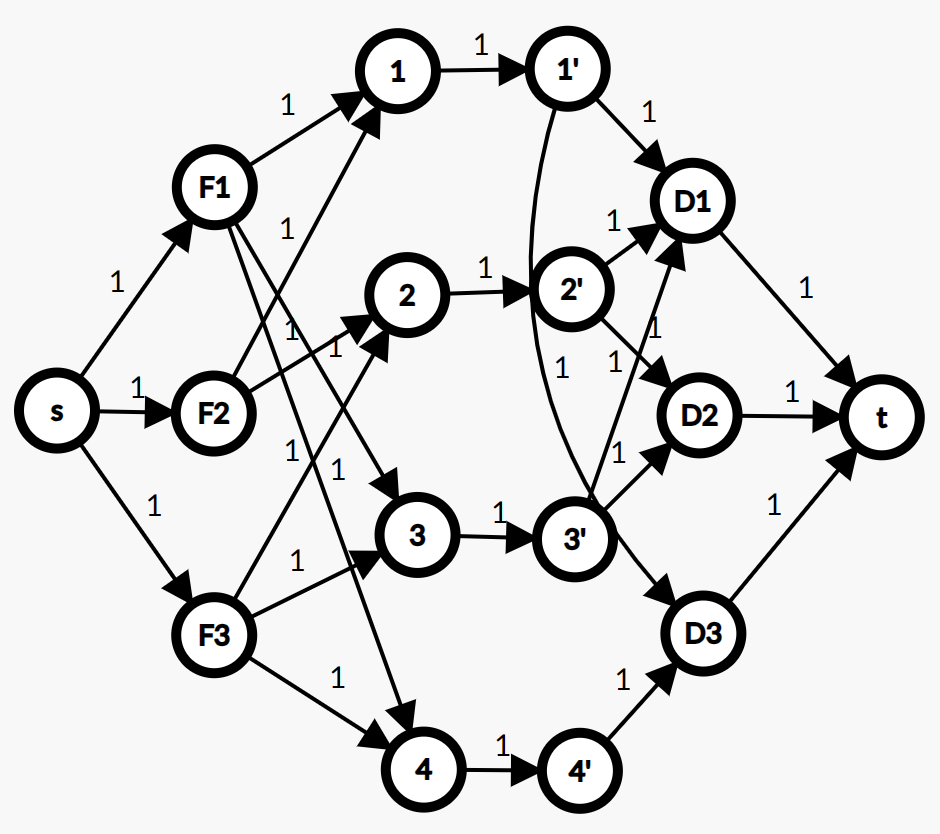通过，流量守恒，就可以使得通过每一个点的流量最多为 $1$，也就满足了题意。 
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 4e2 + 10, M = 1e5 + 10;

int n, m, k, s, t;
int h[N], e[M], ne[M], f[M], idx;
int d[N], cur[N];

void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx ++;
    e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx ++;
}
bool bfs() {
    memset(d, -1, sizeof d);
    queue<int> q;
    q.emplace(s), d[s] = 0, cur[s] = h[s];
    while (q.size()) {
        int u = q.front();
        q.pop();

        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (d[j] == -1 && f[i]) {
                d[j] = d[u] + 1, cur[j] = h[j];
                if (j == t) return 1;
                q.emplace(j);
            }
        }
    }
    return 0;
}
int find(int u, int lim) {
    if (u == t) return lim;

    int flow = 0;
    for (int i = cur[u]; ~i && flow < lim; i = ne[i]) {
        cur[u] = i;
        int j = e[i];
        if (d[j] == d[u] + 1 && f[i]) {
            int tmp = find(j, min(lim - flow, f[i]));
            if (!tmp) d[j] = -1;
            f[i] -= tmp, f[i ^ 1] += tmp, flow += tmp;
        }
    }
    return flow;
}
int dinic() {
    int res = 0, flow;
    while (bfs()) while (flow = find(s, 1e18)) res += flow;
    return res;
}

signed main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    memset(h, -1, sizeof h);
    cin >> n >> m >> k;

    s = 0, t = n * 2 + m + k + 1;
    for (int i = 1; i <= n; i ++) {
        int cf, cd, x;
        cin >> cf >> cd;
        for (int j = 1; j <= cf; j ++)
            cin >> x, add(x, i + m, 1);
        for (int j = 1; j <= cd; j ++)
            cin >> x, add(i + m + n, x + m + n + n, 1);
    }
    for (int i = 1; i <= m; i ++)
        add(s, i, 1);
    for (int i = m + n * 2 + 1; i < t; i ++)
        add(i, t, 1);
    for (int i = m + 1; i <= m + n; i ++)
        add(i, i + n, 1);

    cout << dinic() << endl;

    return 0;
}
习题

P2766 最长不下降子序列问题

参考代码 
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 1e3 + 10, M = 4e5 + 10;

int n, s, t;
int a[N], dp[N];
int h[N], e[M], ne[M], f[M], idx;
int d[N], cur[N];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx ++;
    e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx ++;
}
bool bfs() {
    memset(d, -1, sizeof d);
    queue<int> q;
    q.emplace(s), d[s] = 0, cur[s] = h[s];
    while (q.size()) {
        int u = q.front();
        q.pop();

        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (d[j] == -1 && f[i]) {
                d[j] = d[u] + 1, cur[j] = h[j];
                if (j == t) return 1;
                q.emplace(j);
            }
        }
    }
    return 0;
}
int find(int u, int lim) {
    if (u == t) return lim;

    int flow = 0;
    for (int i = cur[u]; ~i && flow < lim; i = ne[i]) {
        cur[u] = i;
        int j = e[i];
        if (d[j] == d[u] + 1 && f[i]) {
            int tmp = find(j, min(lim - flow, f[i]));
            if (!tmp) d[j] = -1;
            f[i] -= tmp, f[i ^ 1] += tmp, flow += tmp;
        }
    }
    return flow;
}
int dinic() {
    int res = 0, flow;
    while (bfs()) while (flow = find(s, 1e18)) res += flow;
    return res;
}

signed main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    memset(h, -1, sizeof h);
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];
    s = 0, t = 2 * n + 1;

    for (int i = 1; i <= n; i ++) {
        dp[i] = 1, add(i, i + n, 1);
        std::vector<int> opt;
        for (int j = 1; j < i; j ++)
            if (a[j] <= a[i] && dp[j] + 1 > dp[i])
                opt.clear(), opt.emplace_back(j), dp[i] = dp[j] + 1;
            else if (a[j] <= a[i] && dp[j] + 1 == dp[i])
                opt.emplace_back(j);
        for (auto v : opt)
            add(n + v, i, 1);
    }
    int res = 0;
    for (int i = 1; i <= n; i ++)
        res = max(res, dp[i]);
    cout << res << endl;

    for (int i = 1; i <= n; i ++) {
        if (dp[i] == res)
            add(i + n, t, 1);
        if (dp[i] == 1)
            add(s, i, 1);
    }
    res = dinic();
    cout << res << endl;

    for (int i = 0; i < idx; i += 2) {
        if (e[i ^ 1] == 1 && e[i] == 1 + n || e[i ^ 1] == 1 + n && e[i] == t || e[i ^ 1] == s && e[i] == 1)
            f[i] = 1e18;
        else if (e[i ^ 1] == n && e[i] == n + n || e[i ^ 1] == n + n && e[i] == t || e[i ^ 1] == s && e[i] == n)
            f[i] = 1e18;
    }
    res += dinic();
    cout << min(res, n) << endl;

    return 0;
}

POJ3498 March of the Penguins

参考代码 
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 2e2 + 10, M = 2e4 + 10;

int n, s, t;
double ld;
int h[N], e[M], ne[M], f[M], idx;
int d[N], cur[N];
struct Node {
    int x, y;
    int tot, cnt;
    double operator- (const Node &tmp)const {
        int a = x - tmp.x, b = y - tmp.y;
        return sqrt(a * a * 1.0 + b * b * 1.0);
    }
}pg[N];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], f[idx] = c, h[a] = idx ++;
    e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx ++;
}
bool bfs() {
    memset(d, -1, sizeof d);
    queue<int> q;
    q.emplace(s), d[s] = 0, cur[s] = h[s];
    while (q.size()) {
        int u = q.front();
        q.pop();

        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (d[j] == -1 && f[i]) {
                d[j] = d[u] + 1, cur[j] = h[j];
                if (j == t) return 1;
                q.emplace(j);
            }
        }
    }
    return 0;
}
int find(int u, int lim) {
    if (u == t) return lim;

    int flow = 0;
    for (int i = cur[u]; ~i && flow < lim; i = ne[i]) {
        cur[u] = i;
        int j = e[i];
        if (d[j] == d[u] + 1 && f[i]) {
            int tmp = find(j, min(lim - flow, f[i]));
            if (!tmp) d[j] = -1;
            f[i] -= tmp, f[i ^ 1] += tmp, flow += tmp;
        }
    }
    return flow;
}
int dinic() {
    int res = 0, flow;
    while (bfs()) while (flow = find(s, 1e18)) res += flow;
    return res;
}

void solve() {
    cin >> n >> ld;

    int sum = 0;
    for (int i = 1; i <= n; i ++)
        cin >> pg[i].x >> pg[i].y >> pg[i].tot >> pg[i].cnt, sum += pg[i].tot;

    s = 0;
    std::vector<int> res;
    for (t = 1; t <= n; t ++) {
        memset(h, -1, sizeof h);
        idx = 0;
        for (int i = 1; i <= n; i ++) {
            add(s, i, pg[i].tot), add(i, i + n, pg[i].cnt);
            for (int j = 1; j <= n; j ++)
                if (i != j && pg[j] - pg[i] <= ld)
                    add(i + n, j, 1e18);
        }
        if (dinic() == sum)
            res.emplace_back(t);
    }

    if (res.empty())
        cout << -1 << endl;
    else {
        for (auto v : res)
            cout << v - 1 << " ";
        cout << endl;
    }
}

signed main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    int dt;

    cin >> dt;

    while (dt --)
        solve();

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1689854.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Linux取经路】基于信号量和环形队列的生产消费者模型

【Linux取经路】基于信号量和环形队列的生产消费者模型

文章目录 一、POSIX 信号量二、POSIX 信号量的接口2.1 sem_init——初始化信号量2.2 sem_destroy——销毁信号量2.3 sem_wait——等待信号量2.4 sem_post——发布信号量 三、基于环形队列的生产消费者模型3.1 单生产单消费模型3.2 多生产多消费模型3.3 基于任务的多生产多消费模…
阅读更多...
构建健壮的机器学习大数据平台：任务实现与数据治理的关键

构建健壮的机器学习大数据平台：任务实现与数据治理的关键

随着数据驱动决策成为现代企业的核心&#xff0c;构建安全、可靠且可扩展的大数据平台变得至关重要。这样的平台不仅需要支持复杂的机器学习任务&#xff0c;还需要在数据质量、合规性和分发方面提供严格的控制。本文旨在探讨构建大型企业机器学习大数据平台时需要考虑的关键要…
阅读更多...
项目如何有效做资源管理？易趋项目管理软件让资源管理可视化

项目如何有效做资源管理？易趋项目管理软件让资源管理可视化

在项目管理的过程中&#xff0c;有效的资源管理能够确保资源得到合理的分配和使用&#xff0c;避免资源的浪费和冗余&#xff0c;进而提高整体工作效率、确保项目的成功&#xff1b;同时降低组织的运营成本。 但在项目推进过程中&#xff0c;项目经理总会面临各种资源管理的难…
阅读更多...
基于Tensorflow卷积神经网络人脸识别公寓人员进出管理系统

基于Tensorflow卷积神经网络人脸识别公寓人员进出管理系统

欢迎大家点赞、收藏、关注、评论啦 &#xff0c;由于篇幅有限&#xff0c;只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景与意义 随着科技的快速发展和智能化水平的提高&#xff0c;公寓管理面临着越来越多的挑战。传统的公寓…
阅读更多...
HTML静态网页成品作业(HTML+CSS)——我的家乡云南保山介绍网页(3个页面)

HTML静态网页成品作业(HTML+CSS)——我的家乡云南保山介绍网页(3个页面)

&#x1f389;不定期分享源码&#xff0c;关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 &#x1f3f7;️本套采用HTMLCSS&#xff0c;未使用Javacsript代码&#xff0c;共有3个页面。 二、作品演示 三、代…
阅读更多...
轻松同步：将照片从三星手机传输到iPad的简便方法

轻松同步：将照片从三星手机传输到iPad的简便方法

概括 想要在新 iPad 上查看三星照片吗&#xff1f;但是&#xff0c;如果您不知道如何将照片从三星手机传输到 iPad&#xff0c;则无法在 iPad 上查看图片。为此&#xff0c;本文分享了 7 个有用的方法&#xff0c;以便您可以使用它们在不同操作系统之间轻松发送照片。现在&…
阅读更多...
leetcode-盛水最多的容器-109

leetcode-盛水最多的容器-109

题目要求 思路 1.正常用双循环外循环i从0开始&#xff0c;内循环从height.size()-1开始去计算每一个值是可以的&#xff0c;但是因为数据量太大&#xff0c;会超时。 2.考虑到超时&#xff0c;需要优化一些&#xff0c;比如第一个选下标1&#xff0c;第二个选下标3和第一个选下…
阅读更多...
【笔记】从零开始做一个精灵龙女-素模阶段

【笔记】从零开始做一个精灵龙女-素模阶段

事前准备 1.在ps标记好位置先&#xff0c;斜方肌&#xff0c;腰线&#xff0c;耻骨&#xff0c;膝盖&#xff0c;脚 2.导入素模&#xff0c;对好位置 软选择 1.原画上半身很短&#xff0c;所以这里把上半身做的也短一些 选择上半身的点-软选择-衰减调整-箭头调整 如果要调整…
阅读更多...
mysql数据库innodb体系结构（一、内存结构 与二、物理存储结构）

mysql数据库innodb体系结构（一、内存结构 与二、物理存储结构）

文章目录 InnoDB存储引擎结构图innoDB体系结构一、内存结构1.Buffer Pool2.Change Pool3.Log Buffer 二、物理存储结构1.系统表空间2.独立表空间3.Redo日志1、redo 日志 4.Undo日志1、undo 日志 回滚段中的UNDO日志分为两种&#xff1a;UNDO 日志存储结构 InnoDB存储引擎结构图…
阅读更多...
Flat Ads获广东电视台报道！CEO林啸：助力更多企业实现业务全球化增长

Flat Ads获广东电视台报道！CEO林啸：助力更多企业实现业务全球化增长

近日,在广州举行的第四届全球产品与增长展会(PAGC2024)上,Flat Ads凭借其卓越的一站式全球化营销和创新的变现方案大放异彩,不仅吸引了众多业界目光,同时也在展会上斩获了备受瞩目的“金帆奖”,展现了其在全球化营销推广领域的卓越实力和专业服务。 在大会现场,Flat Ads的CEO林…
阅读更多...
差分约束题解

差分约束题解

目录 注意点&#xff1a; 思路&#xff1a; SPFA和Dij的不同点&#xff1a; Dij: SPFA: AC代码&#xff1a; 扩展&#xff1a; 题目链接&#xff1a;【模板】差分约束 - 洛谷 注意点&#xff1a; 注意这一题不能用Dij&#xff0c;只能用SPFA 因为这样子才可以得出这个不…
阅读更多...
【简单介绍下近邻算法】

【简单介绍下近邻算法】

&#x1f308;个人主页: 程序员不想敲代码啊 &#x1f3c6;CSDN优质创作者&#xff0c;CSDN实力新星&#xff0c;CSDN博客专家 &#x1f44d;点赞⭐评论⭐收藏 &#x1f91d;希望本文对您有所裨益&#xff0c;如有不足之处&#xff0c;欢迎在评论区提出指正&#xff0c;让我们共…
阅读更多...
全域运营是割韭菜吗？常见套路有哪些？

全域运营是割韭菜吗？常见套路有哪些？

随着全域运营赛道的全面开启&#xff0c;全域运营服务商和全域运营系统的数量迅速增加&#xff0c;持续激发赛道活力的同时&#xff0c;也让一些试图用全域运营割韭菜的人有了可趁之机。 值得庆幸的是&#xff0c;由于当前全域运营赛道刚兴起不久&#xff0c;因此&#xff0c;割…
阅读更多...
Raylib 绘制自定义字体的一种套路

Raylib 绘制自定义字体的一种套路

Raylib 绘制自定义字体是真的难搞。我的需求是程序可以加载多种自定义字体&#xff0c;英文中文的都有。 我调试了很久成功了&#xff01; 很有用的参考&#xff0c;建议先看一遍&#xff1a; 瞿华&#xff1a;raylib绘制中文内容 个人笔记&#xff5c;Raylib 的字体使用 - …
阅读更多...
Nginx - 健康检查终极指南：探索Upstream Check模块

Nginx - 健康检查终极指南：探索Upstream Check模块

文章目录 概述upstream_check_module模块安装和配置指南模块安装步骤基本配置示例详细配置说明检查类型和参数常见问题及解决方案 SSL检查和DNS解析功能SSL检查配置示例和说明配置示例 DNS解析配置示例和说明配置示例 结合实际应用场景的高级配置示例综合SSL检查与DNS解析 总结…
阅读更多...
代码随想录算法训练营第三天| 203.移除链表元素、 707.设计链表、 206.反转链表

代码随想录算法训练营第三天| 203.移除链表元素、 707.设计链表、 206.反转链表

203.移除链表元素 题目链接&#xff1a; 203.移除链表元素 文档讲解&#xff1a;代码随想录 状态&#xff1a;没做出来&#xff0c;做题的时候定义了一个cur指针跳过了目标val遍历了一遍链表&#xff0c;实际上并没有删除该删的节点。 错误代码&#xff1a; public ListNode re…
阅读更多...
一键恢复安卓手机数据：3个快速简便的解决方案！

一键恢复安卓手机数据：3个快速简便的解决方案！

安卓手机作为我们不可或缺的数字伙伴&#xff0c;承载着大量珍贵的个人和工作数据。然而&#xff0c;随着我们在手机上进行各种操作&#xff0c;不可避免地会遇到一些令人头痛的问题&#xff0c;比如意外删除文件、系统故障或其他不可预见的情况&#xff0c;导致重要数据的丢失…
阅读更多...
springboot基于Web前端技术的java养老院管理系统_utbl7

springboot基于Web前端技术的java养老院管理系统_utbl7

3.普通用户模块包括&#xff1a;普通会员的注册、养老院客房查询、养老院留言查询、预约老人基本信息登记、选择房间、用户缴费的功能。 4.数据信息能够及时进行动态更新&#xff0c;增删&#xff0c;用户搜素方便&#xff0c;使用户可以直接浏览相关信息&#xff0c;要考虑便于…
阅读更多...
埋点——about前端

埋点——about前端

所谓“埋点”&#xff0c;是数据采集领域(尤其是用户行为数据采集领域)的术语&#xff0c;指的是针对特定用户行为或事件进行捕获、处理和发送的相关技术及其实施过程。比如用户某个icon点击次数、观看某个视频的时长等等,埋点的技术实质&#xff0c;是先监听软件应用运行过程中…
阅读更多...
C#数据类型变量、常量

C#数据类型变量、常量

一个变量只不过是一个供程序操作的存储区的名字。 在 C# 中&#xff0c;变量是用于存储和表示数据的标识符&#xff0c;在声明变量时&#xff0c;您需要指定变量的类型&#xff0c;并且可以选择性地为其分配一个初始值。 在 C# 中&#xff0c;每个变量都有一个特定的类型&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023