前言
本笔记介绍了如何使用 Python、pandas 和 SciPy 对天气数据进行基本分析。 它不包含对气象科学的贡献,但说明了如何生成简单的图和基本模型来拟合一些真实的物理观测。
一、相关库引入
import numpy
import scipy.stats
import pandas
import matplotlib.pyplot as plt
plt.style.use("bmh")让我们使用 pandas 库从 wunderground.com 网站下载并导入一些关于 2013 年图卢兹机场(官方代号为“LFBO”)天气状况的数据。 (为方便起见,因为访问历史数据需要创建一个帐户,所以我们下载了 2013 年的数据,稍微清理了一下,然后上传到 risk-engineering.org 网站。)然后我们看前几行 数据,使用 pandas 数据框的 head 方法。
(1)数据读取
data = pandas.read_csv("https://risk-engineering.org/static/data/TLS-weather-data-2013.csv")
data.head()(2)数据查看

数据框的列字段提供对列名称的访问。

二、数据一致性检查
对您的数据进行一些检查是一种很好的做法,以确保您了解列的编码方式并检查内容是否合理。 在 Python 中编写此类检查的一种简单方法是使用 assert 函数编写一些断言。 如果断言失败,Python 将打印错误。
我们可以检查我们拥有数据的天数是否是一年中合理的天数。 我们可以检查每天记录的最高温度是否大于当天的平均值和最低温度,记录的风速也是如此。 我们还可以检查所有风速是否为正。
assert(0 < len(data) <= 365)
for index, day in data.iterrows():
assert(day["Max TemperatureC"] >= day["Mean TemperatureC"] >= day["Min TemperatureC"])
assert(day["Max Wind SpeedKm/h"] >= day["Mean Wind SpeedKm/h"] >= 0)
assert(360 >= day["WindDirDegrees"] >= 0)(1)2013年测得的最低温度查看
def FahrenheitToCelsius(F):
return (F - 32) * 5 / 9.0
# as a basic test, check that our Fahrenheit and Celsius scales intersect at -40
FahrenheitToCelsius(-40)data["Min TemperatureC"].min()
(2)年中的日平均气温是如何变化查看
plt.plot(data["Mean TemperatureC"])
plt.ylabel("Mean daily temperature (°C)");
三、检查随机变量之间的相关性
1 检查各种测量值之间的相关性,例如温度、压力、风速和能见度。
(1)最大温度
plt.scatter(data["Max TemperatureC"], data["Mean Sea Level PressurehPa"])
scipy.stats.pearsonr(data["Max TemperatureC"], data["Mean Sea Level PressurehPa"])
(2)平均温度
plt.scatter(data["Mean TemperatureC"], data["Mean Sea Level PressurehPa"]);
scipy.stats.pearsonr(data["Mean TemperatureC"], data["Mean Sea Level PressurehPa"])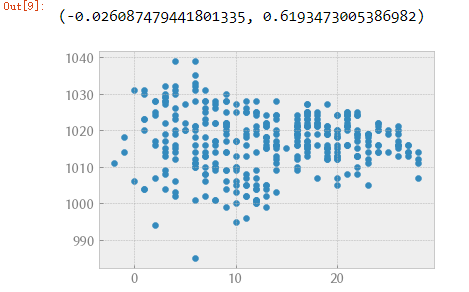
(3)平均能见度
plt.scatter(data["Mean VisibilityKm"], data["Mean Sea Level PressurehPa"])
scipy.stats.pearsonr(data["Mean VisibilityKm"], data["Mean Sea Level PressurehPa"])
2. 检测湿度与温度相关性
露点是空气中水的饱和温度(水蒸气凝结的温度)。 它与温度和湿度水平相关。
data.plot(x="Mean TemperatureC", y="Dew PointC", kind="scatter")
scipy.stats.pearsonr(data["Mean TemperatureC"], data["Dew PointC"])
如果使用概率模型生成用于某些风险计算的天气样本,那么样本尊重输入变量之间的相关性很重要。 否则,可能会在不可能的输入天气变量组合上运行风险模型,而结果将是不切实际的。
三、将概率分布拟合到数据
SciPy 具有允许“拟合”数据的概率分布的功能。 它将计算数据最匹配的分布参数(最低级别的错误)。 首先尝试使用正态分布生成的一些数据。
(1)模拟数据测试
# here we generate some fake "observations"
obs = scipy.stats.norm(loc=10, scale=2).rvs(1000)
scipy.stats.norm.fit(obs)
它告诉我们,根据我们的数据,正态分布的最佳参数是平均值 9.92 和标准差 2.04(实际上,每次运行此笔记本时这些数字都会改变)。 事实上,这非常接近原始参数。 我们可以将我们的“拟合”法线与数据直方图叠加,以直观地检查拟合。
mu, sigma = scipy.stats.norm.fit(obs)
fitted = scipy.stats.norm(mu, sigma)
plt.hist(obs, bins=30, density=True, alpha=0.5);
x = numpy.linspace(obs.min(), obs.max(), 100)
plt.plot(x, fitted.pdf(x), lw=3);
上图可以看出拟合的很好。
(2)气象数据拟合
让我们对图卢兹机场的风速数据进行相同的操作。 一些文献研究表明风速不是正态分布的; 一般服从对数正态分布或威布尔分布。 让我们从尝试拟合对数正态分布(SciPy 中的 scipy.stats.lognorm)开始。
wind = data["Mean Wind SpeedKm/h"]
shape, loc, scale = scipy.stats.lognorm.fit(wind, floc=0)
fitted = scipy.stats.lognorm(shape, loc, scale)
plt.hist(wind, density=True, alpha=0.5)
support = numpy.linspace(wind.min(), wind.max(), 100)
plt.plot(support, fitted.pdf(support), "r-", lw=3)
plt.title("TLS wind speed in 2013", weight="bold")
plt.xlabel("Mean wind speed (km/h)");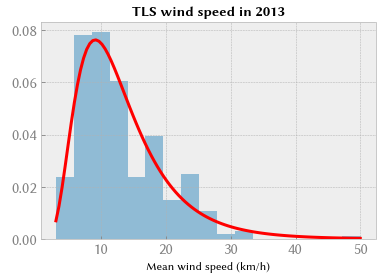
我们使用概率图来直观地检查拟合分布与数据的拟合程度。 这显示了根据理论分布的分位数绘制的样本分位数。 检查它如何适合概率图的边缘(在分布的尾部)尤为重要。 我们首先检查正态分布,发现它不太适合低风速。
wind = data["Mean Wind SpeedKm/h"]
mu, sigma = scipy.stats.norm.fit(wind)
fitted = scipy.stats.norm(mu, sigma)
scipy.stats.probplot(wind, dist=fitted, plot=plt.figure().add_subplot(111))
plt.title("Normal probability plot of TLS wind speed", weight="bold")
# also run a Kolmogorov-Smirnov test to measure goodness of fit
scipy.stats.kstest(wind, "norm")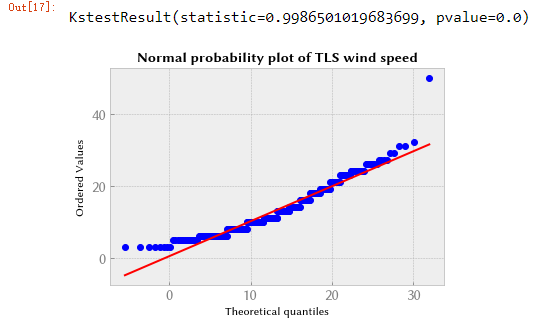
拟合度还不错,除了分布的尾部(低风速和高风速)。 然后我们检查对数正态分布,发现它更适合低风速,而不太适合高风速。
fitted = scipy.stats.lognorm(shape, loc, scale)
scipy.stats.probplot(wind, dist=fitted, plot=plt.figure().add_subplot(111))
plt.title("Lognormal probability plot of TLS wind speed", weight="bold")
scipy.stats.kstest(wind, "lognorm", (shape,loc,scale))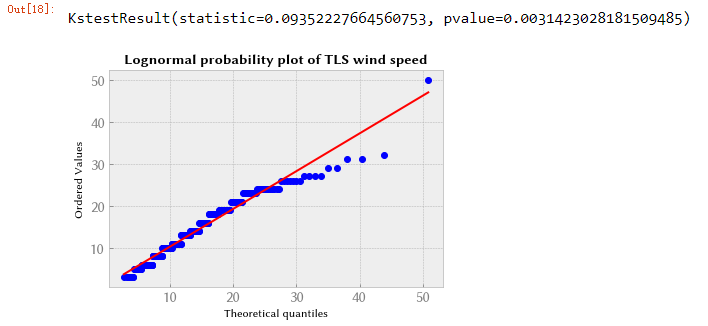
最后,我们检查 Weibull 分布。
p0, p1, p2 = scipy.stats.weibull_min.fit(wind, floc=0)
fitted = scipy.stats.weibull_min(p0, p1, p2)
plt.hist(wind, density=True, alpha=0.5)
plt.plot(support, fitted.pdf(support), "r-", lw=2)
plt.title("Wind speed in TLS in 2013, with Weibull fit", weight="bold")
plt.xlabel("Mean wind speed (km/h)");
scipy.stats.probplot(wind, dist=fitted, plot=plt.figure().add_subplot(111))
plt.title("Weibull probability plot for TLS wind speed", weight="bold")
scipy.stats.kstest(wind, "weibull_min", args=(p0, p1, p2))
四、结论
与对数正态分布相比,Kolmogorov-Smirnov 距离统计对于 Weibull 分布的效果略差。 分位数-分位数图表明,除了一个极值点(可能是异常值)外,它在最高观测风速下更符合观测结果。 如果我们将我们的模型用于优化目的,围绕最常见的风速,我们将选择 Weibull 分布。 如果我们使用模型是为了安全,最高风速是最危险的,我们会改用对数正态图,因为它可以更好地预测观察到的最高风速。