一、异或运算：

1.1 Demo

0和N进行异或运算都等于N

任何一个数和自己异或运算都等于0

且异或运算满足交换率 a^b = b^a

eg： a = 甲 ， b = 已 那么则有 a = a^b

​ b = a^b

​ a = a^b

故有： 进行第一个式子之后 则有 a = 甲 ^ 已； b = 已

  												a = 甲 ^已； b = 甲 ^ 已 ^ 已  = 甲 ^ 0;  则b = 甲 因为任意两个相同的数 进行与运算都等于0

​ 此时在进行第二个式子的运算则有：

​ a = 甲 ^ 已 ^ 甲； a = 已；

​ 再进过第三个式子 则有 a = 已； 因为此时 a = 已 ^ 甲 ^ 甲； a = 已；

注意 以上操作的前提是 a和b 在内存中是两个独立的区域

package com.xc.dataStruct.异或运算;

/**
 * @project untitled
 * @description
 * @author capture or new
 * @date 2024/5/24 15:13:58
 * @version 1.0
 */
public class Demo {
    /**
     *  0和N进行异或运算都等于N
     *  任何一个数和自己异或运算都等于0
     *  且异或运算满足交换率 a^b = b^a
     *  eg： a = 甲 ， b = 已  那么则有 a = a^b
     *                              b = a^b
     *                              a = a^b
     *                          故有： 进行第一个式子之后 则有 a = 甲 ^ 已； b = 已
     *                                                   a = 甲 ^已； b = 甲 ^ 已 ^ 已  = 甲 ^ 0;  则b = 甲 因为任意两个相同的数 进行与运算都等于0
     *                                                   此时在进行第二个式子的运算则有：
     *                                                      a = 甲 ^ 已 ^ 甲； a = 已；
     *                                                   再进过第三个式子 则有 a = 已； 因为此时 a = 已 ^ 甲 ^ 甲； a = 已；
     *
     *        注意 以上操作的前提是 a和b 在内存中是两个独立的区域
     **/
    public static void main(String[] args) {
//        接下来演示两个数的交换测试
        int a = 10;
        int b = 40;
        getSwap(a, b);
    }

    private static void getSwap(int a, int b) {
       a = a^b;
       b = a^b;
       a = a^b;
        System.out.println(a);
        System.out.println(b);
    }
}

1.2 面试题

package com.xc.dataStruct.异或运算;

/**
 * @project untitled
 * @description
 * @author capture or new
 * @date 2024/5/24 15:33:26
 * @version 1.0
 */
public class 面试题 {
    /**
     * O（n）时间和 O（1）空间
     * 在一个数组中 一种数出现了奇数次 其他数出现了偶数次 求这个数
     * 第二问： 两种数出现了奇数次，其他数都出现了偶数次。求这两个数
     **/
    public static void main(String[] args) {
        one();
        two();
    }

    // 第一问  前面说到位运算满足结合律 我们这里 虽然是有很多数，但是奇数个只有一种。我们可以看做将有偶数个个数的数进行先放到一堆进行异或运算后再最后对那个只有奇数个数的数进行异或运算，到最后肯定就只剩下了0^那个数  eg： 3^3^3 = 0^3 = 3
    public static void one(){
        int arr[] = {2,3,2,1,5,1,5};
        int eor = 0;
        for (int i = 0; i < arr.length; i++) {
            eor ^= arr[i];
        }
        System.out.println(eor);
    }
    // 第二问
    /**
     * 第一步：首先我们使用eor 从到到尾进行异或运算，因为有两种奇数个个数的数，所以异或到最后肯定只剩下了eor = a^b,且肯定不等于零，a不等于b
     * 第二步：对于位运算来说 一个整数有32位，我们进行上面的第一轮异或运算后只剩下了a^b,之后我们要获取到这两个数，两个数不相等在位运算中，则定然有这两个中存在某一位不等，一个整数的那个位为0另一个整数的那个数为1.
     * 第三步：这样我们可以根据位再次将数数组分为两组，一组是那个位为0 的数，一组则是那个位为1的数。之后我们再次创建一个eor` 进行再次与运算这样我们就获取到了a或者是b。
     * 第四步：这样 eor = a^b, eor` = a。 这样我们又回到了原始状态了的异或运算了。两个数异或运算这样就得到了b。 实现了对两种数的计算了。
     **/
    public static void two(){
        int arr[] = {2,3,2,1,5,1,5,9};
        // 先使用eor 进行从头到尾进行一次异或运算
        int eor = 0;
        for (int i = 0; i < arr.length; i++) {
            eor ^= arr[i];
        }

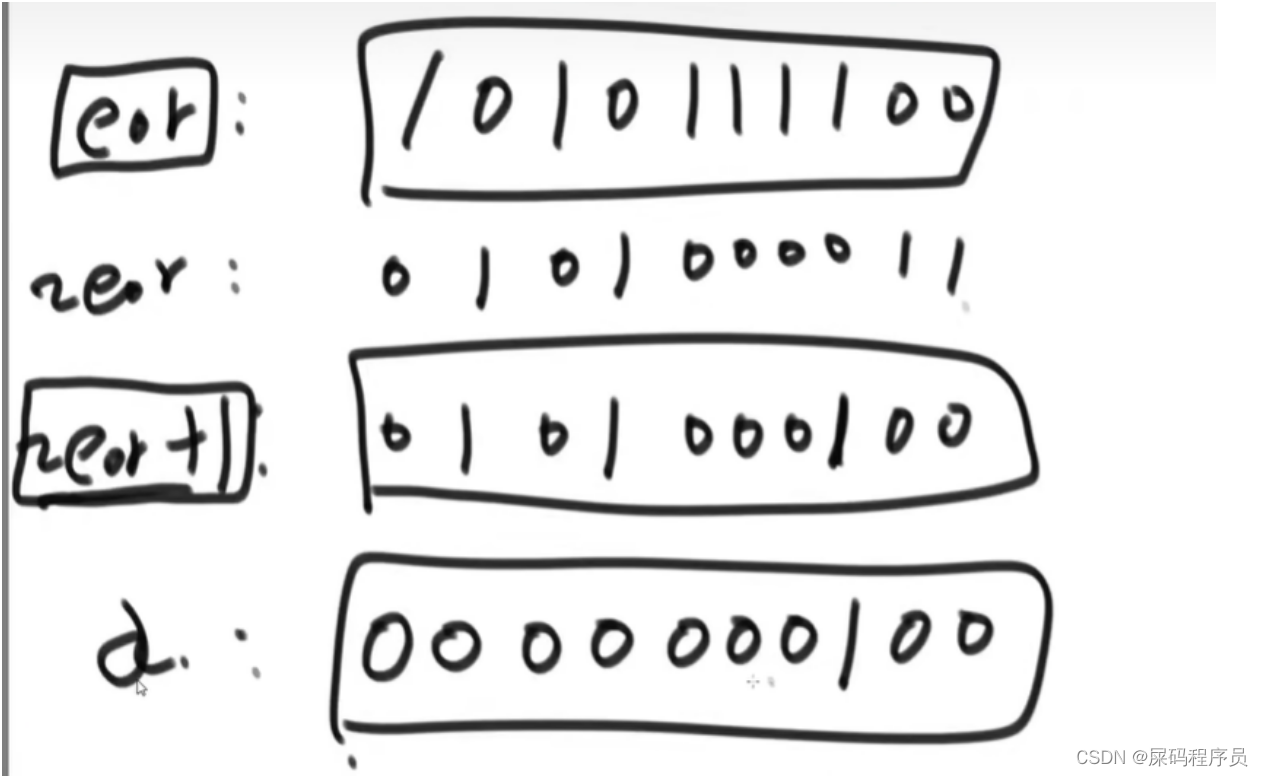
        // 取出一个不为零的数的最右侧的1  。也就是两组数中不同的哪一位，这里假设为最右侧的哪一位。
        int rightOne = eor & (~eor + 1);

        int onlyOne = 0; //eor`
        for (int i = 0; i < arr.length; i++) {
            if ((arr[i] & rightOne) == 0){ // 进行与运算，这里我们就是要计算出a 或者是b，只有相同的哪一位才是我们想要的哦。
                onlyOne ^= arr[i];
            }
        }

        System.out.println(onlyOne + " " +(onlyOne ^ eor));
    }
}

（位运算）提取出一个不等于零的数的最右侧的1