Java方法的递归
- 前言
- 一、递归的概念
- 示例
- 代码示例
- 二、递归执行过程分析
- 代码示例
- 执行过程图
- 三、递归练习
- 代码示例
- 按顺序打印一个数字的每一位(例如 1234 打印出 1 2 3 4)
- 递归求 1 + 2 + 3 + ... + 10
- 写一个递归方法,输入一个非负整数,返回组成它的数字之和. 例如,输入 1729, 则应该返回1+7+2+9,它的和是19
- 求斐波那契数列的第 N 项
- 斐波那契数列介绍
前言
Java方法的递归是指一个Java方法直接或间接地调用自身,以完成重复或嵌套的计算任务。递归常用于处理具有自相似性的问题,通过分解问题为更小、更简单的子问题来解决整个问题。递归方法需要明确定义递归终止条件,以防止无限循环。
一、递归的概念
一个方法在执行过程中调用自身, 就称为 “递归”.
递归相当于数学上的 “数学归纳法”, 有一个起始条件, 然后有一个递推公式.
递归是一种在方法内调用自身的编程技术。在使用递归时,方法会重复调用自身,每次调用时传递不同的参数,直到满足某个终止条件为止。
递归可以用于解决一些问题,特别是那些具有递归结构的问题。在这些问题中,解决方案可以通过将问题分解为更小的子问题来实现。每次递归调用都会处理一个子问题,直到达到基本情况,然后将子问题的解决方案组合起来得到原始问题的解决方案。
递归要求在每次调用时,传递给递归方法的参数应该与原始问题的参数有关,但规模更小。这样可以确保递归在每次调用时朝着基本情况前进,并最终达到终止条件。
递归的基本思想是将一个大问题分解为一个或多个相同类型的小问题,然后解决每个小问题,并将它们的解决方案组合起来得到原始问题的解决方案。递归方法必须有一个基本情况,以便在基本情况下终止递归调用。
在Java中,递归可以用于解决各种问题,例如计算阶乘、斐波那契数列、遍历树等。但需要注意的是,递归可能会导致栈溢出的错误,因为每次递归调用都会将方法的调用信息存储在栈中。因此,递归需要谨慎使用,并确保有适当的终止条件。
示例
求 N!
起始条件: N = 1 的时候, N! 为 1. 这个起始条件相当于递归的结束条件.
递归公式: 求 N! , 直接不好求, 可以把问题转换成 N! => N * (N-1)!
代码示例
递归求 N 的阶乘
class Main{
public static void main(String[] args) {
int n = 5;
int ret = factor(n);
System.out.println("ret = " + ret);
}
public static int factor(int n) {
if (n == 1) {
return 1;
}
return n * factor(n - 1); // factor 调用函数自身
}
}
二、递归执行过程分析
递归的程序的执行过程不太容易理解, 要想理解清楚递归, 必须先理解清楚 “方法的执行过程”, 尤其是 “方法执行结束之后, 回到调用位置继续往下执行”.
代码示例
递归求 N 的阶乘, 加上日志版本
class Main{
public static void main(String[] args) {
int n = 5;
int ret = factor(n);
System.out.println("ret = " + ret);
}
public static int factor(int n) {
System.out.println("函数开始, n = " + n);
if (n == 1) {
System.out.println("函数结束, n = 1 ret = 1");
return 1;
}
int ret = n * factor(n - 1);
System.out.println("函数结束, n = " + n + " ret = " + ret);
return ret;
}
}

执行过程图
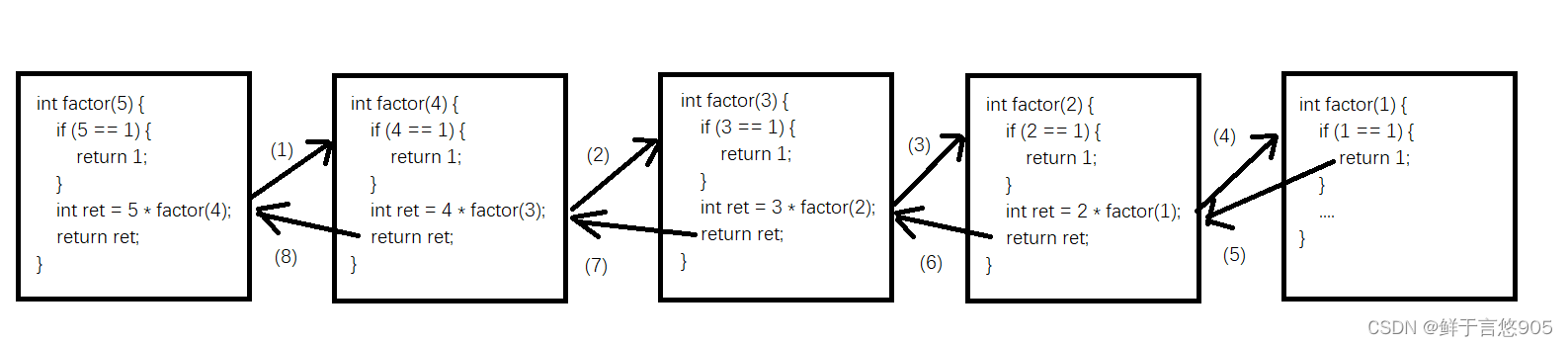
程序按照序号中标识的 (1) -> (8) 的顺序执行.
关于 “调用栈”
方法调用的时候, 会有一个 “栈” 这样的内存空间描述当前的调用关系. 称为调用栈.
每一次的方法调用就称为一个 “栈帧”, 每个栈帧中包含了这次调用的参数是哪些, 返回到哪里继续执行等信息.
三、递归练习
代码示例
按顺序打印一个数字的每一位(例如 1234 打印出 1 2 3 4)
public static void print(int num) {
if (num > 9) {
print(num / 10);
}
System.out.println(num % 10);
}
递归求 1 + 2 + 3 + … + 10
public static int sum(int num) {
if (num == 1) {
return 1;
}
return num + sum(num - 1);
}
写一个递归方法,输入一个非负整数,返回组成它的数字之和. 例如,输入 1729, 则应该返回1+7+2+9,它的和是19
public static int sum(int num) {
if (num < 10) {
return num;
}
return num % 10 + sum(num / 10);
}
求斐波那契数列的第 N 项
斐波那契数列介绍
斐波那契数列是一个数学上的数列,其形式为 1, 1, 2, 3, 5, 8, 13, 21, 34, …。数列中的每个数字都是前面两个数字之和。也就是说,第三个数字是前两个数字之和,第四个数字是前两个数字之和,以此类推。
斐波那契数列最早由13世纪的意大利数学家斐波那契(Fibonacci)发现和研究,他在其著作《算盘书》中介绍了这个数列,并将其应用于兔子繁殖的模型中。
斐波那契数列在数学中有着重要的应用和性质。它在自然界中也有许多出现的现象,例如植物的叶子排列、螺旋壳的形状等都可以用斐波那契数列来描述。
斐波那契数列也有一些有趣的特性,例如当数列中的数字趋近无穷时,相邻两个数字的比值会趋近于黄金分割比例0.618。这个黄金分割比例在艺术和设计中也有广泛的应用。
斐波那契数列除了以上的介绍,还有其他的许多性质和应用,它在数学中被广泛研究和讨论。
public static int fib(int n) {
if (n == 1 || n == 2) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}
当我们求 fib(40) 的时候发现, 程序执行速度极慢. 原因是进行了大量的重复运算.
class Main {
public static int count = 0; // 这个是类的成员变量. 后面会详细介绍到.
public static void main(String[] args) {
System.out.println(fib(40));
System.out.println(count);
}
public static int fib(int n) {
if (n == 1 || n == 2) {
return 1;
}
if (n == 3) {
count++;
}
return fib(n - 1) + fib(n - 2);
}
}

可以使用循环的方式来求斐波那契数列问题, 避免出现冗余运算.
class Main {
public static int count = 0; // 这个是类的成员变量. 后面会详细介绍到.
public static void main(String[] args) {
System.out.println(fib(40));
System.out.println(count);
}
public static int fib(int n) {
int last2 = 1;
int last1 = 1;
int cur = 0;
for (int i = 3; i <= n; i++) {
cur = last1 + last2;
last2 = last1;
last1 = cur;
}
return cur;
}
}