2024-5-23,星期四,22:20,天气:晴,心情:晴。今天没有什么重要的事情发生,心情一如既往的平静,距离返校假期还有两天~~~。
今天观看了石群老师电路基础课程的第23/24个视频,开始了一阶、二阶电路的学习,主要学习内容为:动态电路、动态电路方程的推导(RC、RL、RLC、高阶电路)、电路的初始条件及例题;C语言方面开启了第六章的学习,并继续完善总结C语言学习笔记。
1. 动态电路
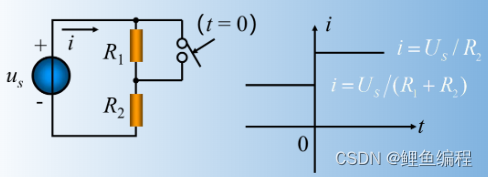
含有动态元件电容和电感的电路称动态电路。当动态电路状态发生改变时(换路)需要经历一个变化过程才能达到新的稳定状态。这个变化过程称为电路的过渡过程。从下面一电阻电路可以看出,在非动态电路中,这一过渡期为零。
但从下面含电容的电路中可以看出,动态电路存在一明显过渡期(电感电路类似)。
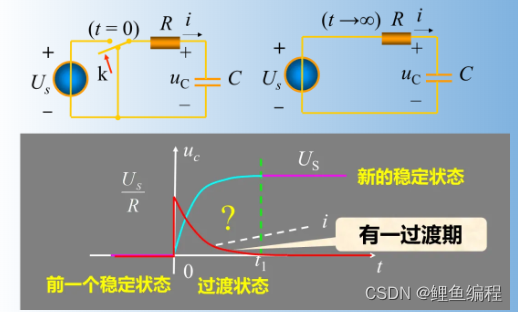
工程实际中在切断电容或电感电路时会出现过电压和过电流现象。
换路:
电路结构、状态发生变化,包括支路的连接和断开,电路参数的变化。
过渡过程产生的原因:
电路内部含有储能元件L、C,电路在换路时能量发生变化,而能量的储存和释放都需要一定的时间来完成。

2. 动态电路的方程
RC电路方程推导:
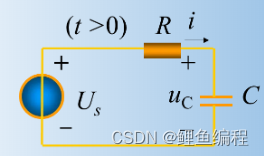

RL电路方程推导:
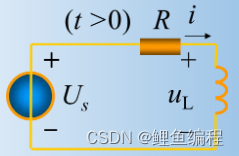

综上,含有一个动态元件电容或电感的线性电路,其电路方程为一阶线性常微分方程,称一阶电路。

RLC电路方程推导:
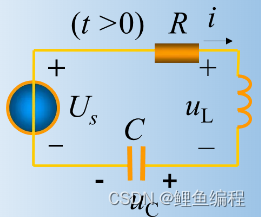
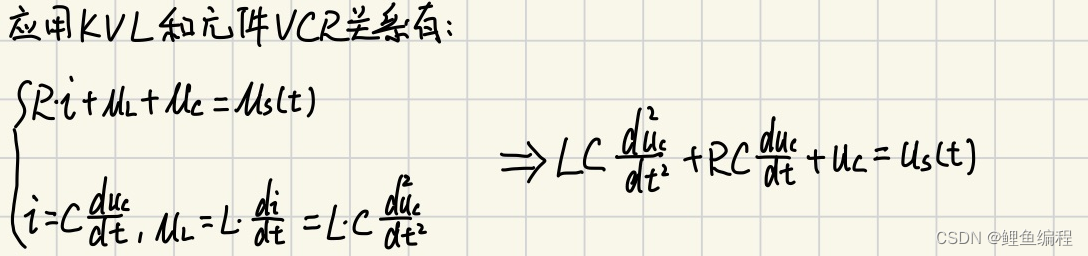
含有二个动态元件的线性电路,其电路方程为二阶线性常微分方程,称二阶电路。
综合上述分析可以看出:描述动态电路的电路方程为微分方程;动态电路方程的阶数通常等于电路中动态元件的个数。
(a)一阶电路:一阶电路中只有一个动态元件,描述电路的方程是一阶线性微分方程。
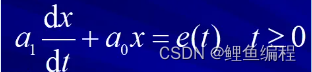
(b)二阶电路:二阶电路中有二个动态元件,描述电路的方程是二阶线性微分方程。
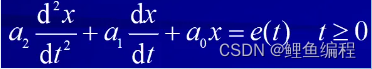
(c)高阶电路:电路中有多个动态元件,描述电路的方程是高阶微分方程。
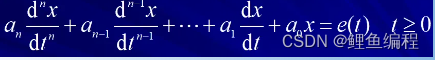
电路的稳态分析与动态分析:
(a)稳态分析包括:恒定或周期性激励;换路发生很长时间后状态;微分方程的特解。
(b)动态分析包括:任意激励;换路发生后的整个过程;微分方程的通解。
3. 电路的初始条件
电容的初始条件推导:
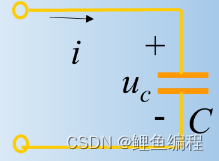
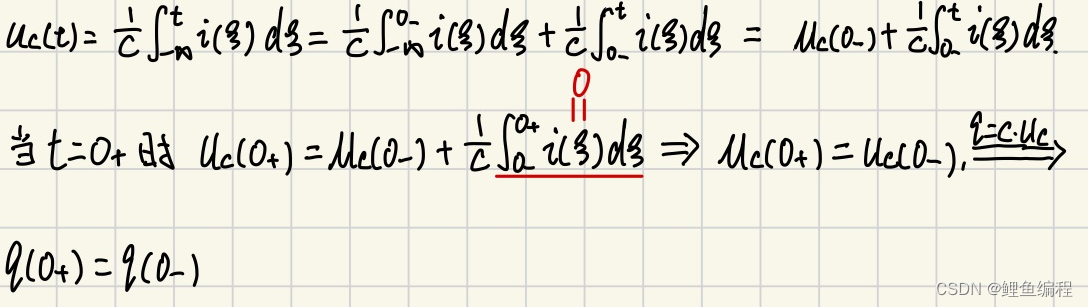
综上可知,换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变。
电感的初始条件推导:
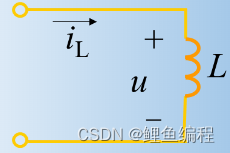
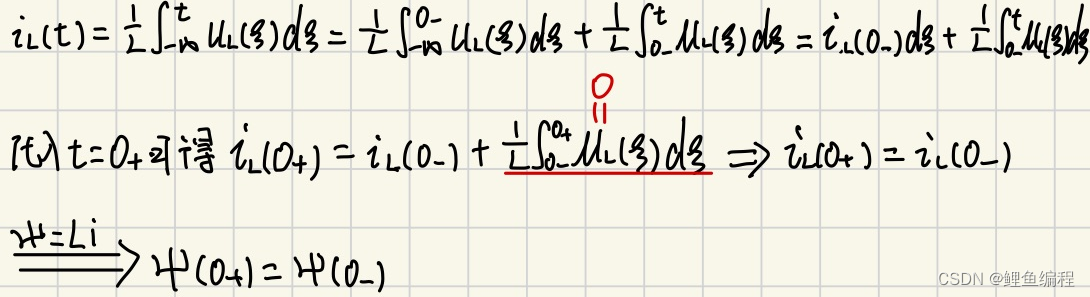
综上可知,换路瞬间,若电感电压保持为有限值, 则电感电流(磁链)换路前后保持不变。
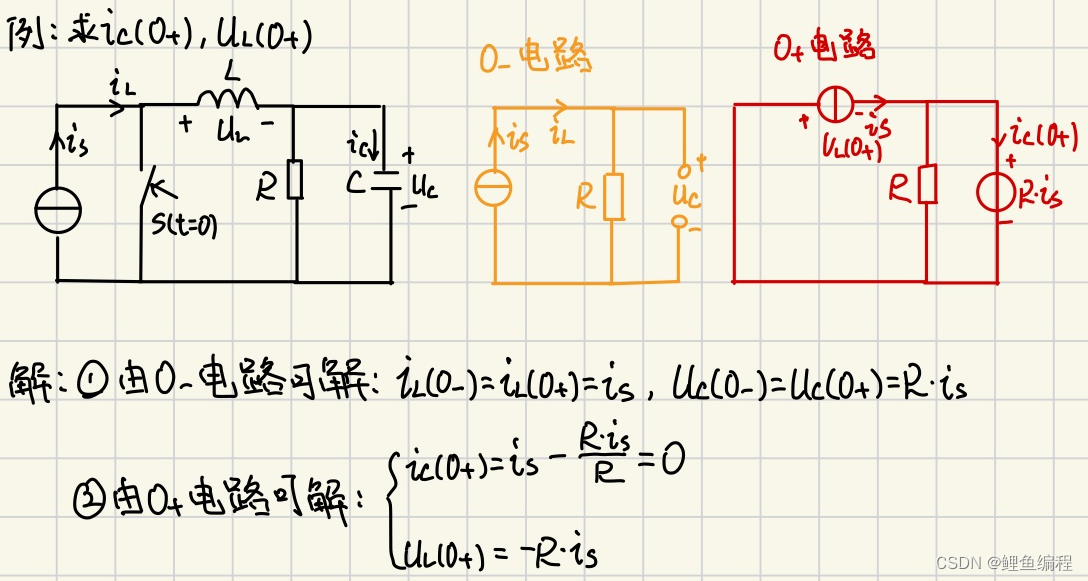
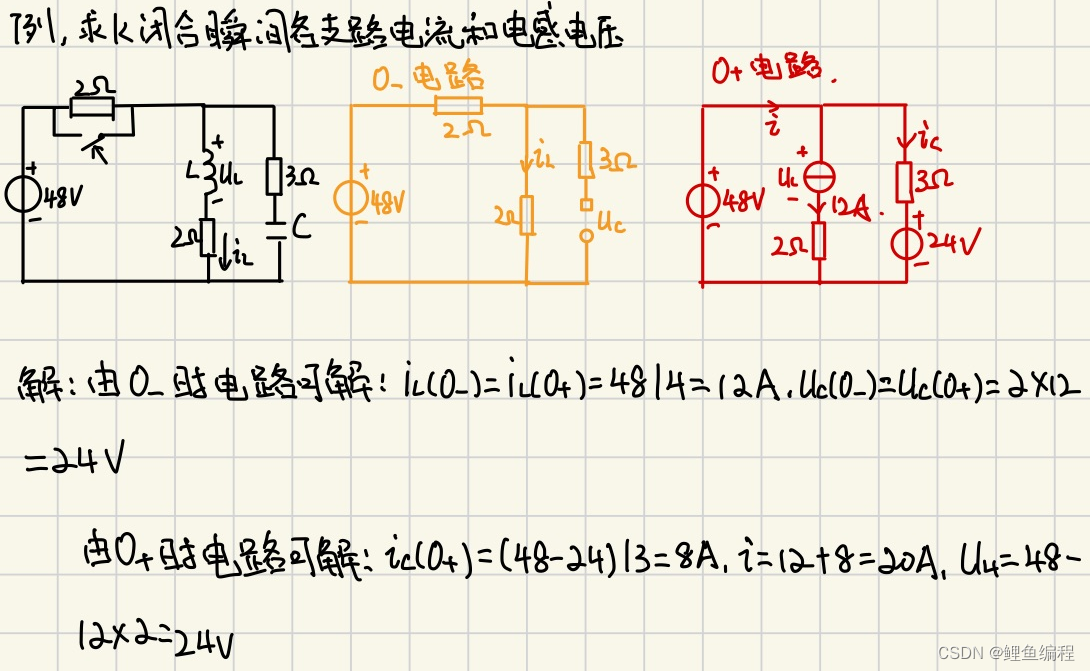
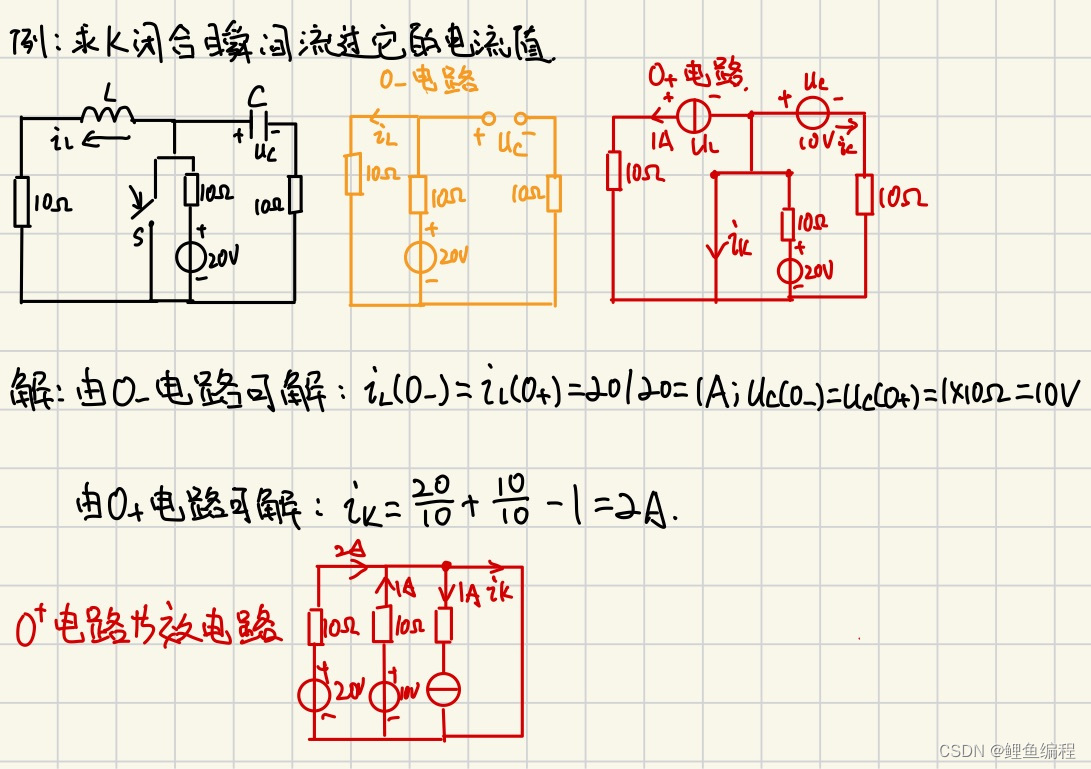
电路初始值的确认:
(1)由换路前电路(稳定状态)求uC(0-)和iL(0-)
(2)由换路定律得uC(0+) 和 iL(0+)
(3)画0+等效电路:电容用电压源替代(无电压相当于导线);电感用电流源替代(无电流相当于开路),方向与原假定方向相同
(4)由0+电路求所需各变量的0+值。
今日总学习时长约4h30min,明日学习内容为:电路基础的第25、26个视频内容;C语言第六章(第七章)内容。