- 什么是进制?
是数学中的一个概念,就是数据“逢几进位”。
例如:生活中用的计数方法 ---- 十进制。十进制就是数字逢十就要进一位。
例如:一个星期有7天,就是逢七进一;一个月有30天就是逢30进一;一年有365天就是逢365进一;一分有60秒,就是逢60进一。诸如此类的还有很多!!!
说的专业一点,进制就是进位制,是人们规定的一种进位方法。对于任何一种进制 ---- X 进制,就表示某一位置上的数运算时是逢X进一位。二进制就是逢二进一,八进制就是逢八进一,十进制就是逢十进一,十六进制就是逢十六进一。
- Java 针对整数常量提供了4种表现形式
二进制
八进制
十进制
十六进制
- 为什么会有二进制、八进制、十六进制?
有二进制的原因是因为计算机最底层的电子元器件只有两种状态 ---- 高电平和低电平(有电和没电)。任何数据在计算机中都是以二进制的形式存在的,二进制早期由电信号开关演变而来。一个整数在内存中一样也是二进制的,但是使用一大串的1或者0组成的数值进行使用很麻烦!
有八进制、十六进制的原因是因为二进制表示同样的数值太长不方便阅读和记忆,二八进制和十六进制较短,方便阅读和记忆。
- 计算机中存储单位的换算
什么是 bit(比特)?
二进制:001 每一位都是一个 bit , 二进制只能是 0/1 两个数字组成,是计算机中一个最小的信号单元, 可能是高电平或者是低电平。
什么是 byte (字节)?
1个 bit 只能表示两种信号或者两种状态,表示的范围很小!因为我们的英文字母就有26个,两种状态很明显不够表示。所以国际化标准组织就规定把8个 bit 归为一组作为一个数据的最小的单元!
8bit = 1byte;
1kb = 1024byte; (kb是千字节 ---- 2 的 10 次方)
1mb = 1024kb;
1gb = 1024mb;
1tb = 1024gb;
计算机中最小的信号单位是bit, 而最小的信息单位是 byte
1个bit只有两种状态,也就是只有两个数 ---- 0 和 1
因为一个 bit 能表现出的状态(信息)太少,英文字母列表就有26哥,还有标点符号,所以国际化标准组织就规定 8 个 bit 为一组,用来表示一个信息单元!
我们知道一位二进制数就可以表示两个状态,两个2进制数可以表示4种状态,3个二进制数可以表示8种状态。其中的规律就是几位二进制数可以表示的状态数量是 2 的 “位数” 次幂。
例如:
1位二进制数可以表示的状态的个数就是 2 种:
0 / 1
2位二进制数可以表示的状态的个数就是 2 的 2 次幂,等于 4 种;
00 / 01 / 10 / 11
3位二进制数可以表示的状态的个数就是 2 的 3 次幂,等于 8 种;
000 / 001 / 010 / 011 / 100 / 101 / 110 / 111
8位二进制数可以表示的状态的个数就是 2 的 8 次幂,等于256 种
- 不同进制的组成
二进制
由 0,1 组成。以 0b 开头
八进制
由 0,1, … , 7 组成。以 0 开头
十进制
由 0,1, … , 9 组成。整数默认是十进制的
十六进制
由 0,1, … , 9,a,b,c,d,e,f (大小写均可)。以 0x 开头
实战程序:
练习题:演示100在各种不同进制中所表示的数据是多少?
package com.tyler.demo;
/**
* @author: TylerZhong
* @description:
*/
public class Demo02 {
public static void main(String[] args) {
/**
* 练习题:演示100在各种不同进制中所表示的数据是多少?
*/
int a = 100; // 十进制
System.out.println(a); // 十进制
System.out.println("-----------------------");
int b = 0b100; // 二进制, b 可以是大写也可以是小写
System.out.println(b); // 十进制
System.out.println("-----------------------");
int c = 0100; // 八进制
System.out.println(c); // 十进制
System.out.println("-----------------------");
int d = 0x100; // 十六进制, x 可以是大写,也可以是小写
System.out.println(d); // 十进制
System.out.println("-----------------------");
}
}
- 不同进制数据之间的计算
十进制数据之间的计算
10 + 10 = 20
二进制数据之间的计算
0b1101 + 0b1101010 = 0b1110111
/**
* 1 1 0 1
* 1 1 0 1 0 1 0
* --------------------
* 1 1 1 0 1 1 1
*/
八进制数据之间的计算
0127 + 0765 = 01114
/**
* 1 2 7
* 7 6 5
* ----------
* 1 1 1 4
*/
十六进制数据之间的计算
0x1ab + 0x99a = 0xb45
a = 10
b = 11
c = 12
d = 13
e = 14
f = 15
/**
* 1 a b
* 9 9 a
* ----------
* b 4 5
*/
- 进制转换
》》其它进制到十进制
把系数 * 基数的权次幂相加即可。
》》系数:就是每一位上的数据。
》》基数:X进制,基数就是X.
》》权:在右边,从0开始编号,对应位上的编号即为该位的权。
实战程序:
package com.tyler.demo;
/**
* @author: TylerZhong
* @description:
*/
public class Demo03 {
public static void main(String[] args) {
/**
* 进制转换
* 任意进制到十进制之间的转换
* 二进制、八进制、十六进制的数据如何转换成十进制
*
* 前提:
* 系数:每一个位上的数字(157,个位的系数是7;十位上的系数是5;百位上的系数是1)
* 基数:几进制基数就是几(十进制基数就是10)
* 权:一个数据从右往左数,从0开始,对每一位数据进行编号,那么这个编号就是这个位置上的数字的权
*
* 规律:
* 任意进制到十进制的转换都等于“这个数据的各个位上的系数乘以基数的权次幂相加的和”
*
* 十进制:157 = 7*10^0 + 5*10^1 + 1*10^2 = 7 + 50 + 100 = 157
*
* 二进制:0b110
* 转成
* 十进制: 0*2^0 + 1*2^1 + 1*2^2 = 0 + 2 + 4 = 6
*
* 八进制:0110
* 转成
* 十进制:0*8^0 + 1*8^1 + 1*8^2 = 0 + 8 + 64 = 72
*
* 十六进制:0XABC
* 转成
* 十进制: 12*16^0 + 11*16^1 + 10*16^2 = 12 + 176 + 2560 = 2748
*/
int n = 0b110;
System.out.println(n);
int b = 0110;
System.out.println(b);
int c = 0XABC;
System.out.println(c);
}
}
》》十进制到其他进制
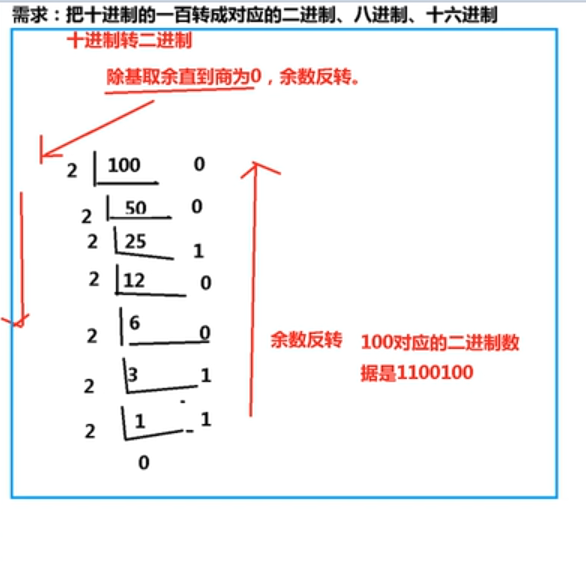
除基数取余数,直到商位0, 余数反转
/**
* 进制转换
* 十进制到任意进制之间的转换
* 十进制转成二进制、八进制、十六进制
*
* 规则:除基数取余数,直到商位0, 余数反转
*
* 需求: 把十进制的100分别转成二进制、八进制、十六进制
*/


- 十进制和二进制的快速转换
8421码
8421码是中国大陆的叫法,8421码是BCD码中最常用的一种。
在这种编码方式中每一位二进制代码的1都是代表一个固定数值,把每一位的1代表的十进制数加起来,得到的结果就是它所代表的十进制数码。
什么是BCD码?
BCD码(Binary-Coded decimal?)亦称二进码十进数或二-十进制代码。用4位二进制数来表示1位十进制数中的0~9这10个数码。是一种二进制的数字编码形式,用二进制编码的十进制代码。
BCD码展示:
/**
* 二进制: 1 1 1 1 1 1 1 1
* 十进制: 128 64 32 16 8 4 2 1
*/
二进制和八进制,十六进制如何转换
以 十进制 作为桥梁
二进制到 八进制 3 位组合
二进制到 十六进制 4 位组合
- 有符号数据表示法
什么是有符号数?
所谓有符号数就是数据有正负之分就是有符号数,数据无正负之分就是无符号数。
例如:+7、-7 就是有符号数。
有符号数的组成
因为在计算机内,有符号数有3种表示法:原码、反码和补码。而且所有数据的运算都是采用补码进行的。
符号位+数值位(例如:int i = +7;)(00000000000000000000000000000111)
+7、和 -7 在计算机中是如何存储的!
什么是原码
就是二进制定点表示法,即最高位为符号,“0”表示正,“1”表示负,其余位表示数值的大小。
什么是反码
正数的反码与其原码相同,负数的反码是对其原码逐位取反,但符号除外。
什么是补码
补码就是在反码的基础上+1就是补码
代码实战:
package com.tyler.demo;
/**
* @author: TylerZhong
* @description:
*/
public class Demo01 {
public static void main(String[] args) {
/**
* +7、和 -7 在计算机中是如何存储的!
* 有符号数由两部分组成:
* 1、符号位(二进制的最左边的一位表示的是符号位,0 表示的是正数,1表示的负数)
* 2、数值位
*
* int 类型的表数范围:2的32次方个数
* -2的31次方 到 +2的31次发方 - 1
*/
// int i = +7;
int i = 0b00000000000000000000000000000111;
System.out.println(i);
// int j = -7;
// -7的二进制位
// 0b10000000000000000000000000000111;
int j = 0b10000000000000000000000000000111; //-2147483641 不是-7,那为什么呢?
// 计算机中存储有符号数的时候是按照补码的形式存进去的。
// 此数据 0b10000000000000000000000000000111 不是二进制的补码,而是二进制的原码
// 什么是原码、什么是反码、什么是补码?
// 计算机中所有的有符号数据都是按照补码的形式存储的
// 正数的原码、反码、补码都一样
// 负数的原码、反码、补码是不一样的
// 什么是原码? 就是符号位+数值位(数据的绝对值)
// 什么是反码? 反码就是符号位不变,其它位全部1变0,0变1
// 什么是补码? 补码就是在反码的基础上+1就是补码
/**
* +7:
* 原码:0b00000000000000000000000000000111
* 反码:0b00000000000000000000000000000111
* 补码:0b00000000000000000000000000000111
*
* -7:
* 原码:0b10000000000000000000000000000111
* 反码:0b11111111111111111111111111111000
* 补码:0b11111111111111111111111111111001
*/
j = 0b11111111111111111111111111111001; // -7的补码
// 计算机在现实给我们看的时候,会把补码转换成原码
// 怎么转?
// 补码 - 1 得到反码, 反码再取反得到就是原码(符号位不变)
// 补码:0b11111111111111111111111111111001
// 反码:0b11111111111111111111111111111000
// 原码:0b10000000000000000000000000000111 // -7的原码
System.out.println(j);
}
}
- ** 位运算(位指的是二进制位或者是bit位)**
计算机中所有的计算到计算机底层中都会编程位运算(就是二进制位的运算)。位运算可以提高程序的效率!而且以后如果我们研究JDK或者某个框架的原码,会发现很多地方都用到了位运算!
- 位运算符的种类
&: 按位与
| : 按位或
^ :按位异或
~ :按位取反
<< : 左移
>> : 右移
>>> : 无符号右移
位运算符连接的操作数是什么?数值类型(二进制)
位运算表达式的结果是什么?数值类型
实战程序:
package com.tyler.demo;
/**
* @author: TylerZhong
* @description:
*/
public class Demo04 {
public static void main(String[] args) {
/**
* 位运算符种类:
* & : 按位与 规则:两个同为 1 的时候才为 1
* | : 按位或 规则:两个中只要有一个为 1,那么结果就为 1
* ^ : 按位异或 规则:两个不一样的时候才为 1,如果一样,就为 0
* ~ : 按位取反(逻辑非的意思是一样的) 规则:1 变 0,0 变 1
*/
/**
* 按位与 &
* 3 & 4 结果是多少?
* 在进行位运算的时候要把数据转换成二进制位!并且全部都是二进制的补码形式!
* 3 的二进制: 0b00000000000000000000000000000011
* 4 的二进制: 0b00000000000000000000000000000100
* 3和4按位与: 0b00000000000000000000000000000000
*/
int i = 3 & 4;
System.out.println(i);
/**
* 按位与 |
* 3 & 4 结果是多少?
* 在进行位运算的时候要把数据转换成二进制位!并且全部都是二进制的补码形式!
* 3 的二进制: 0b00000000000000000000000000000011
* 4 的二进制: 0b00000000000000000000000000000100
* 3和4按位或: 0b00000000000000000000000000000111
*/
i = 3 | 4;
System.out.println(i);
/**
* 按位异或 ^
* 3 ^ 4 结果是多少?
* 在进行位运算的时候要把数据转换成二进制位!并且全部都是二进制的补码形式!
* 3 的二进制: 0b00000000000000000000000000000011
* 4 的二进制: 0b00000000000000000000000000000100
* 3和4按位或: 0b00000000000000000000000000000111
*/
i = 3 ^ 4;
System.out.println(i);
/**
* 按位取反 ~
* ~3 结果是多少?
* 3 的二进制: 0b00000000000000000000000000000011
* 取反结果: 0b11111111111111111111111111111100 // 此数据在计算机中得到的结果是 补码,并且该数是一个 负数
*
* 已知补码求反码?补码 - 1 之后取反(取反的过程中符号位不变)
* 补码:原码取反 + 1 (取反的过程中符号位不变)
*
* 补码: 0b11111111111111111111111111111100
* 减 1: - 1
* ----------------------------------------------------------
* 0b11111111111111111111111111111011
* 取反(原码): 0b10000000000000000000000000000100 // 取反的时候符号位不变
*/
i = ~3;
System.out.println(i);
}
}
package com.tyler.demo;
/**
* @author: TylerZhong
* @description:
*/
public class Demo05 {
public static void main(String[] args) {
/**
* 按位异或的常见应用: 一般应用在加密上
* 一个数据对相同的数据异或两次其值不变
* 数据 a
* 数据 b
* a 两次异或 b ,结果还是 a
* a ^ b ^ b == a
*/
int a = 3;
int b = 4;
System.out.println(a^b^b);
}
}
package com.tyler.demo;
/**
* @author: TylerZhong
* @description:
*/
public class Demo06 {
public static void main(String[] args) {
/**
* 按位异或的常见应用:实现两个变量值的交换
*/
// 实现两个变量值的方式一:通过一个中间变量
int i = 10;
int j = 20;
int c;
c = i;
i = j;
j = c;
System.out.println("i:" + i);
System.out.println("j:" + j);
// 实现两个变量值交换的方式二:通过位运算实现
/**
* int a = 10;
* int b = 20;
*
* a = a ^ b;
* b = a ^ b; -- b = a ^ b ^ b;
* a = a ^ b; -- a = a ^ a ^ b;
*/
int a = 10;
int b = 20;
a = a ^ b;
b = a ^ b;
a = a ^ b;
System.out.println("a:"+a);
System.out.println("b:"+b);
}
}
package com.tyler.demo;
/**
* @author: TylerZhong
* @description:
*/
public class Demo07 {
public static void main(String[] args) {
/**
* << : 左移 : 让操作数乘以 2 的 n 次幂, n 就是移动的位数
* >> : 右移 : 让操作数乘以 2 的 n 次幂, n 就是移动的位数
* >>> : 无符号右移
*
* 格式:
* 操作数 << 往左移动的位数
* 操作数 >> 往右移动的位数
* 操作数 >>> 往右移动的位数
*/
// 左移 <<
int i;
i = 3 << 2; // 操作数 3 * 2^2 = 12
/**
* 3 << 2
* 3 的二进制位:
* 00000000000000000000000000001100
* 往左边移动两位,右边就空出两位!左边移动的两位就被挤掉了,右边空出的两位用0补全
*/
System.out.println(i);
// 右移 >>
i = 32 >> 2; // 操作数 32 / 2^2 = 8
/**
* 32 >> 2
* 32 的二进制位:
* 00000000000000000000000000001000
* 往右边移动两位,左边就空出两位!右边的两位就被挤掉了,左边空出的位置,用符号位的值填充(符号位是1就用1填充,是0就用0填充)
*/
System.out.println(i);
// 右移 >>
i = -32 >> 2;
/**
* -32 >> 2
* -32 的二进制位:
* 原码:10000000000000000000000000100000
* 反码:11111111111111111111111111011111
* 补码:11111111111111111111111111100000
*
* -32 往右移动两位:
* 11111111111111111111111111111000 --- 补码
* 根据补码求源码:
* 11111111111111111111111111111000
* 减 1: - 1
* -----------------------------------------------
* 反码: 11111111111111111111111111110111
* 原码: 10000000000000000000000000001000
*
* 往右边移动两位,左边就空出两位!右边的两位就被挤掉了,左边空出的位置,用符号位的值填充(符号位是1就用1填充,是0就用0填充)
*/
System.out.println(i);
/**
* 无符号右移 >>> 作用也是操作数乘以 2 的 n 次幂
* 无符号右移和右移的区别是:右移操作之后,左边会有空位置出来,空位置用该操作数的符号位置的数不全;无符号右移,左边空出来的位置统统用0补全
* 结论:整数的无符号右移和右移操作的结果是一样的
*/
i = 32 >>> 2; // 操作数 32 / 2^2 = 8
// 00000000000000000000000000001000
System.out.println(i);
i = -32 >>> 2;
/**
* 原码: 10000000000000000000000000100000
* 反码: 11111111111111111111111111011111
* 补码: 11111111111111111111111111100000
* 无符号右移2位:
* 00111111111111111111111111111000
* 负数右移之后,编程了一个正数!
*/
System.out.println(i);
}
}
注意:
进行位运算的时候所有的操作数全部都是二进制,并且是补码!!!
当显示给我们看的时候全部都是原码!!!
此章内容来自B站 “Java讲师孙探” UP主的课程,课程链接 零基础学Java_02进制转换和位运算专题