后端分类

1. 基于滤波器的后端。常见的扩展卡尔曼EKF，无迹卡尔曼UKF，粒子滤波PF，或者是fastlio2中使用的误差状态卡尔曼ESIKF（本质上迭代过程等效于高斯牛顿法，优化当前帧的状态）。还有许多其他滤波器，本质上是基于一阶马尔可夫性假设，就是认为当前的状态$x_k$只与$x_{k-1}$有关，与历史之前的状态无关，来简化卡尔曼滤波过程中预测更新的运算。
2. 基于非线性优化的后端。这种方法就可以考虑第k帧之前所有历史帧的状态，类似一个全局的思维，通过构建全局状态的优化问题，来优化所有帧的状态（包括位姿和特征点），特别能够依靠回环检测来提高状态的全局一致性。
3. 滑动窗口滤波和优化。
   （1）滑动窗口滤波其实应该就是基于滤波器的后端的一个变种，认为一阶马尔可夫性假设太极端了，所以想选择一定数量的关键帧，共同考虑多个帧去解算出当前帧的状态。
   （2）滑动窗口优化应该也是基于非线性优化的后端的一个变种，认为随着SLAM过程，关键帧增多，优化耗时会增加，所以想选择一些离当前时刻接近的关键帧而不是全部关键帧来一起优化

基于滤波器的后端

这里首先将状态的符号简化，状态包含相机位姿（$x_k$）和特征点（$y_m$）。
x k =  def  { x k , y 1 , … , y m } \boldsymbol{x}_k \stackrel{\text { def }}{=}\left\{\boldsymbol{x}_k, \boldsymbol{y}_1, \ldots, \boldsymbol{y}_m\right\} xk​= def {xk​,y1​,…,ym​}
那么经典的运动和观测方程就可以简化：（注意状态上的符号，$\hat{\mathbf{x}}$代表状态的后验，$\check{\mathbf{x}}$代表状态的预测，这个定义是为了跟slam14讲ppt里一致）
$$\{\begin{array}{l}{\mathbf{x}}_k=f\left({\hat{\mathbf{x}}}_{k-1},{\mathbf{u}}_k\right)+{\mathbf{w}}_k\\ {\mathbf{z}}_k=h\left({\mathbf{x}}_k\right)+{\mathbf{v}}_k\end{array}k=1,\dots ,N$$
我们已知的是k-1时刻状态的后验${\hat{x}}_{k-1}$和输入$u_k$，想求的是当前k时刻状态${\hat{x}}_k$的后验分布
$$P\left({\hat{\mathbf{x}}}_k\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k}\right)$$
根据贝叶斯法则，书上给出的式子是这样的：
$$P\left({\hat{\mathbf{x}}}_k\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k}\right)\propto P\left({\mathbf{z}}_k\mid {\check{\mathbf{x}}}_k\right)P\left({\check{\mathbf{x}}}_k\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k-1}\right)$$

但是在我看来，假设了一阶马尔可夫性，直接都可以简化成最基本的贝叶斯滤波的形式。
$$P\left({\hat{\mathbf{x}}}_k\mid {\hat{\mathbf{x}}}_{k-1},{\mathbf{u}}_k,{\mathbf{z}}_k\right)\propto P\left({\mathbf{z}}_k\mid {\check{\mathbf{x}}}_k\right)P\left({\check{\mathbf{x}}}_k\mid {\hat{\mathbf{x}}}_{k-1},{\mathbf{u}}_k\right)$$
很明显上面式子中左边的是当前k时刻状态${\hat{x}}_k$的后验分布，右边的第一项是似然分布，第二项是预测即先验分布。因为后验分布、似然分布和先验分布都属于高斯分布，所以就可以通过经典的卡尔曼滤波公式来求当前k时刻状态${\hat{x}}_k$的后验分布。

线性系统和卡尔曼滤波

如果考虑线性系统，那就是经典的卡尔曼滤波系统。运动方程和观测方程可以由下面的式子表示：
$$\{\begin{array}{l}{\mathbf{x}}_k={\mathbf{A}}_k{\mathbf{x}}_{k-1}+{\mathbf{u}}_k+{\mathbf{w}}_k\\ {\mathbf{z}}_k={\mathbf{C}}_k{\mathbf{x}}_k+{\mathbf{v}}_k\end{array}k=1,\dots ,N$$
其中过程噪声${\mathbf{w}}_k\sim N(0,\mathbf{R})$ 和观测噪声${\mathbf{v}}_k\sim N(0,\mathbf{Q})$ 都服从高斯分布。然后就是根据卡尔曼滤波的5个步骤，求出后验估计${\hat{x}}_k$。
$${\check{\mathbf{x}}}_k={\mathbf{A}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{u}}_k\text{\hspace{1em}(1)}$$

$${\check{\mathbf{P}}}_k={\mathbf{A}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{A}}_k^{\mathrm{T}}+\mathbf{R}\text{\hspace{1em}(2)}$$

$$\mathbf{K}={\check{\mathbf{P}}}_k{\mathbf{C}}_k^{\mathrm{T}}{\left({\mathbf{C}}_k{\check{\mathbf{P}}}_k{\mathbf{C}}_k^{\mathrm{T}}+{\mathbf{Q}}_k\right)}^{-1}\text{\hspace{1em}(3)}$$

$${\hat{\mathbf{x}}}_k={\check{\mathbf{x}}}_k+\mathbf{K}\left({\mathbf{z}}_k-{\mathbf{C}}_k{\check{\mathbf{x}}}_k\right)\text{\hspace{1em}(4)}$$

$${\hat{\mathbf{P}}}_k=\left(\mathbf{I}-\mathbf{K}{\mathbf{C}}_k\right){\check{\mathbf{P}}}_k\text{\hspace{1em}(5)}$$

于是这就得到了后验${\hat{x}}_k$的均值和协方差，用于k+1时刻的预测。

非线性系统和扩展卡尔曼滤波

本质上是在卡尔曼滤波基础上对运动方程和观测方程进行线性化（一阶泰勒展开），在此基础上也是经过5个公式推出$x_k$的后验分布。这里就不展开了，公式都是大同小异。

BA优化

主要就是通过Bundle Adjustment（BA），来构建最小二乘问题，通过非线性优化的方法优化相机位姿和特征点的位置。
下面这个图就很好描述了相机的观测方程：

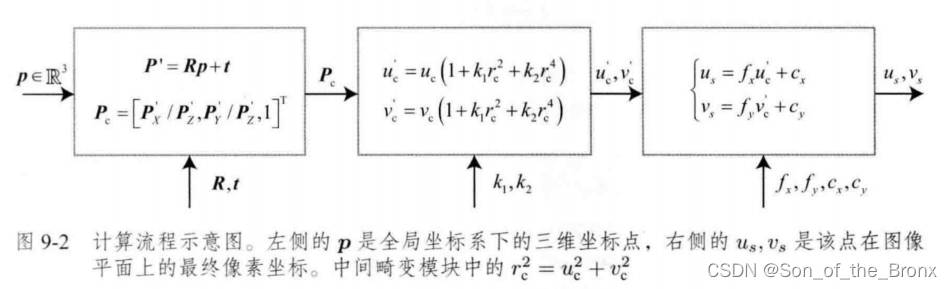
然后就是根据其他时刻的相机与特征点，构建出全局的重投影误差
$$\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\Vert {\mathbf{e}}_{ij}\Vert }^2=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\Vert {\mathbf{z}}_{ij}-h\left({\mathbf{T}}_i,{\mathbf{p}}_j\right)\Vert }^2$$
其中i是相机位姿的序号，j就是相机位姿i看到的特征点。
为了优化这个目标函数，需要求目标函数对相机位姿和特征点的雅可比，然后通过高斯牛顿来优化相机位姿和特征点：
$$\frac{1}{2}\Vert f(\mathbf{x}+\Delta \mathbf{x}){\Vert }^2\approx \frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n{\Vert {\mathbf{e}}_{ij}+{\mathbf{F}}_{ij}\Delta {\mathbf{\xi }}_i+{\mathbf{E}}_{ij}\Delta {\mathbf{p}}_j\Vert }^2$$
其中状态x定义成所有待优化的变量：
$$\mathbf{x}={\left[{\mathbf{T}}_1,\dots ,{\mathbf{T}}_m,{\mathbf{p}}_1,\dots ,{\mathbf{p}}_n\right]}^{\mathrm{T}}$$
${\mathbf{F}}_{ij}$和${\mathbf{E}}_{ij}$分别是误差对相机位姿和特征点的偏导。
最后的优化问题也可以简化成：
$$\frac{1}{2}\Vert f(\mathbf{x}+\Delta \mathbf{x}){\Vert }^2=\frac{1}{2}{\Vert \mathbf{e}+\mathbf{F}\Delta {\mathbf{x}}_c+\mathbf{E}\Delta {\mathbf{x}}_p\Vert }^2$$
最后根据高斯牛顿法，都是需要求解一个增量方程
$$\mathbf{H}\Delta \mathbf{x}=\mathbf{g}$$
对于高斯牛顿法，H矩阵就是
$$\mathbf{H}={\mathbf{J}}^{\mathrm{T}}\mathbf{J}=\left[\begin{array}{ll}{\mathbf{F}}^{\mathrm{T}}\mathbf{F}& {\mathbf{F}}^{\mathrm{T}}\mathbf{E}\\ {\mathbf{E}}^{\mathrm{T}}\mathbf{F}& {\mathbf{E}}^{\mathrm{T}}\mathbf{E}\end{array}\right]$$

实际上这个H矩阵由于特征点的个数往往很多，所以H矩阵规模很大，直接求逆会很耗时，但是H矩阵是有一定的结构，利用这个结构可以加速优化过程。

H矩阵的稀疏性和边缘化

首先这里书本举一个例子说明：

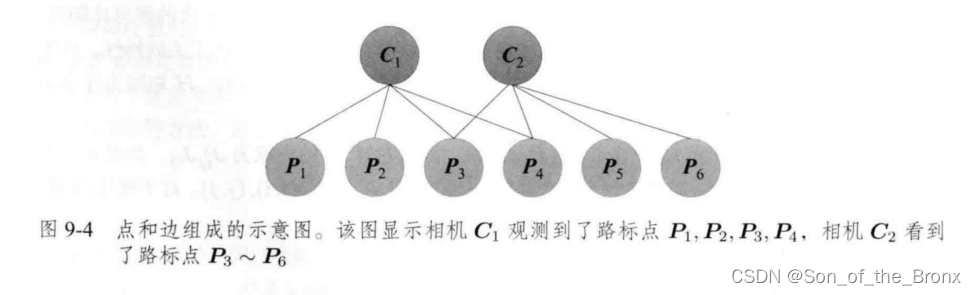
其中图中有$C_1$和$C_2$两个相机位姿和六个特征点，连线代表有观测关系。
这时全局重投影的目标函数为
$$\frac{1}{2}\left({\Vert {\mathbf{e}}_{11}\Vert }^2+{\Vert {\mathbf{e}}_{12}\Vert }^2+{\Vert {\mathbf{e}}_{13}\Vert }^2+{\Vert {\mathbf{e}}_{14}\Vert }^2+{\Vert {\mathbf{e}}_{23}\Vert }^2+{\Vert {\mathbf{e}}_{24}\Vert }^2+{\Vert {\mathbf{e}}_{25}\Vert }^2+{\Vert {\mathbf{e}}_{26}\Vert }^2\right)$$
首先以$e_{11}$对状态x求偏导，可以得到下面的雅可比

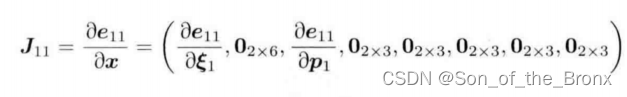
同理其他误差的雅可比都会有这种形式：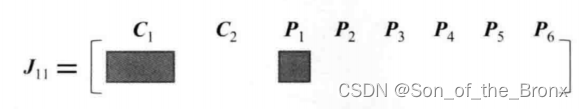
整体的雅可比J和H矩阵就会如同下图所示

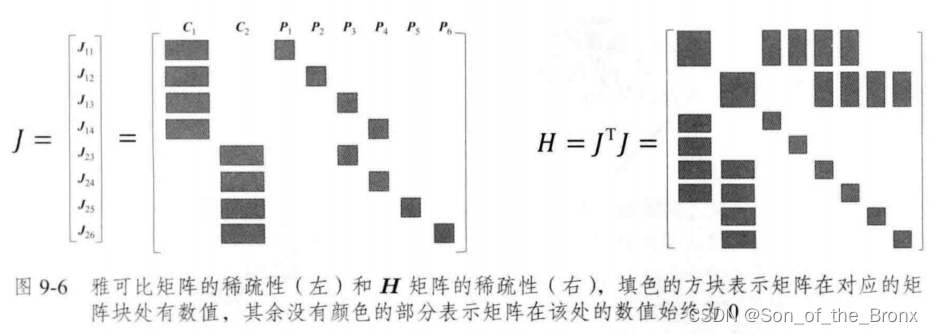
然后对H矩阵进行下图的划分：

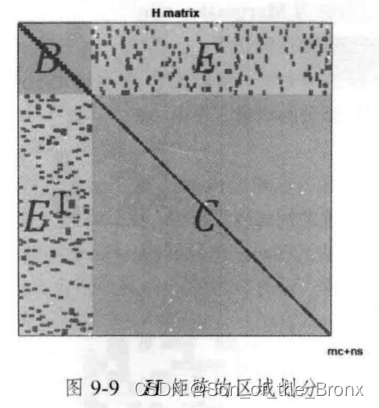
增量方程也可以按照划分，变成下面的形式
$$\left[\begin{array}{ll}\mathbf{B}& \mathbf{E}\\ {\mathbf{E}}^{\mathrm{T}}& \mathbf{C}\end{array}\right]\left[\begin{array}{l}\Delta {\mathbf{x}}_{\mathrm{c}}\\ \Delta {\mathbf{x}}_p\end{array}\right]=\left[\begin{array}{l}\mathbf{v}\\ \mathbf{w}\end{array}\right]$$

对这个线性方程组的求解可以通过边缘化（可通过schur消元进行边缘化，也就是书中的方法。当然也有其他方法进行边缘化，本质都是加快增量方程的求解速度）。边缘化的过程如下：
$$\left[\begin{array}{cc}\mathbf{I}& -\mathbf{E}{\mathbf{C}}^{-1}\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}\mathbf{B}& \mathbf{E}\\ {\mathbf{E}}^{\mathrm{T}}& \mathbf{C}\end{array}\right]\left[\begin{array}{c}\Delta {\mathbf{x}}_{\mathrm{c}}\\ \Delta {\mathbf{x}}_p\end{array}\right]=\left[\begin{array}{cc}\mathbf{I}& -\mathbf{E}{\mathbf{C}}^{-1}\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{c}\mathbf{v}\\ \mathbf{w}\end{array}\right]$$
最终整理得到：
$$\left[\begin{array}{cc}\mathbf{B}-\mathbf{E}{\mathbf{C}}^{-1}{\mathbf{E}}^{\mathrm{T}}& 0\\ {\mathbf{E}}^{\mathrm{T}}& \mathbf{C}\end{array}\right]\left[\begin{array}{l}\Delta {\mathbf{x}}_{\mathrm{c}}\\ \Delta {\mathbf{x}}_p\end{array}\right]=\left[\begin{array}{c}\mathbf{v}-\mathbf{E}{\mathbf{C}}^{-1}\mathbf{w}\\ \mathbf{w}\end{array}\right]$$
因为右上角为0，就可以先把$\Delta {\mathbf{x}}_{\mathrm{c}}$计算出来，因为c是对角块矩阵，所以它的求逆相对简单。将求出$\Delta {\mathbf{x}}_{\mathrm{c}}$后再带入原方程就可以解出$\Delta {\mathbf{x}}_{\mathrm{p}}$。

H矩阵求解的总结

这个边缘化的概念是从概率论的角度来看的。实际上这个求解步骤就是固定$\Delta {\mathbf{x}}_{\mathrm{p}}$，然后求解$\Delta {\mathbf{x}}_{\mathrm{c}}$，最后再算出$\Delta {\mathbf{x}}_{\mathrm{p}}$。从概率公式上：
$$P\left({\mathbf{x}}_{\mathrm{c}},{\mathbf{x}}_p\right)=P\left({\mathbf{x}}_{\mathrm{c}}\mid {\mathbf{x}}_p\right)P\left({\mathbf{x}}_p\right)$$
最终是求得了${\mathbf{x}}_{\mathrm{c}}$的条件概率分布，和${\mathbf{x}}_{\mathrm{p}}$的边缘分布，所以称边缘化。在消元的时候实际上是将特征点的部分信息融入了求解${\mathbf{x}}_{\mathrm{c}}$的过程，所以${\mathbf{x}}_{\mathrm{c}}$是条件概率分布。

需要注意的是，这个边缘化在滑动窗口的方法中也有所应用。

位姿图优化

位姿图优化在视觉SLAM中可以看成是BA优化的简化版。因为BA优化需要将特征点考虑进去，优化的变量包括相机位姿和特征点的位置，大部分是放在特征点优化上了，所以位姿图的意义在于构建一个只有轨迹的图优化问题，特征点看成是一帧相机位姿中确定的点，不再去优化特征点的位置，省去了大量特征点优化的计算。

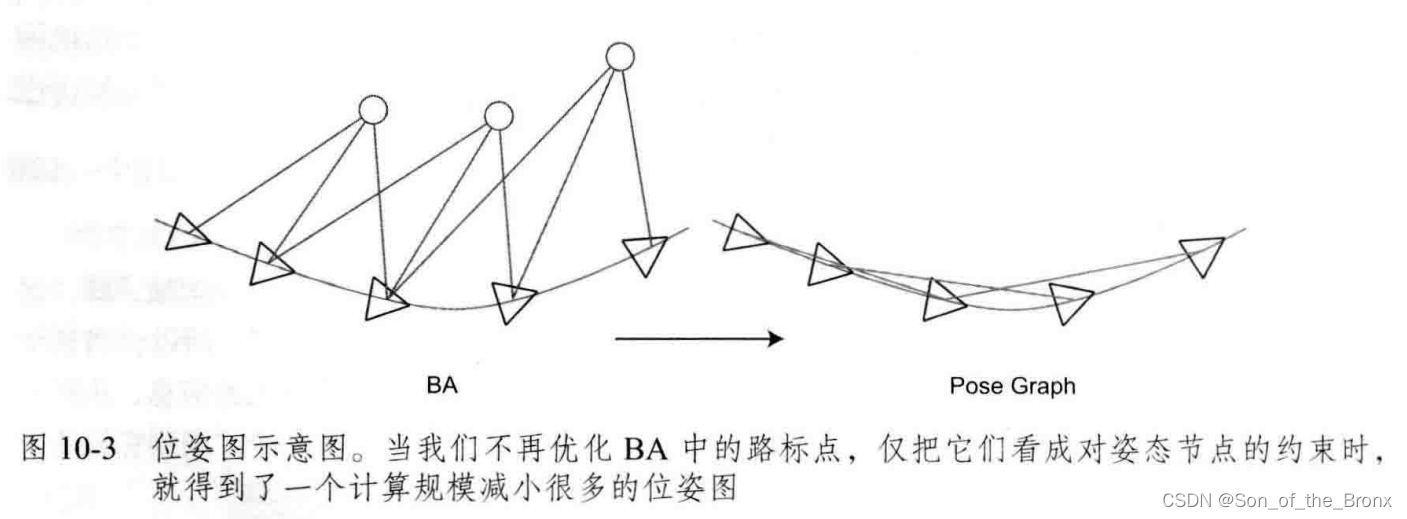
公式推导

假设通过IMU积分或者视觉slam估计了$T_i$和$T_j$之间的一个运动$\Delta {\mathbf{T}}_{ij}$，然后取他们李群之间的差值对应的李代数为误差：
$${\mathbf{e}}_{ij}=\Delta {\mathbf{\xi }}_{ij}=\ln {\left({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}{\mathbf{T}}_j\right)}^{\vee }$$

紧接着就是经典的对$T_i$和$T_j$加左扰动对扰动求导
$${\hat{\mathbf{e}}}_{ij}=\ln {\left({\mathbf{T}}_{ij}^{-1}{\mathbf{T}}_i^{-1}\exp \left({\left(-\mathbf{\delta }{\mathbf{\xi }}_i\right)}^{\wedge }\right)\exp \left(\delta {\mathbf{\xi }}_j^{\wedge }\right){\mathbf{T}}_j\right)}^{\vee }$$
因为上式扰动项被夹在中间，所以可以通过下面的伴随性质：
$$\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{T}=\mathbf{T}\exp \left({\left(\mathrm{Ad}\left({\mathbf{T}}^{-1}\right)\mathbf{\xi }\right)}^{\wedge }\right)$$
将扰动挪到最右边，最终得到下面的式子：

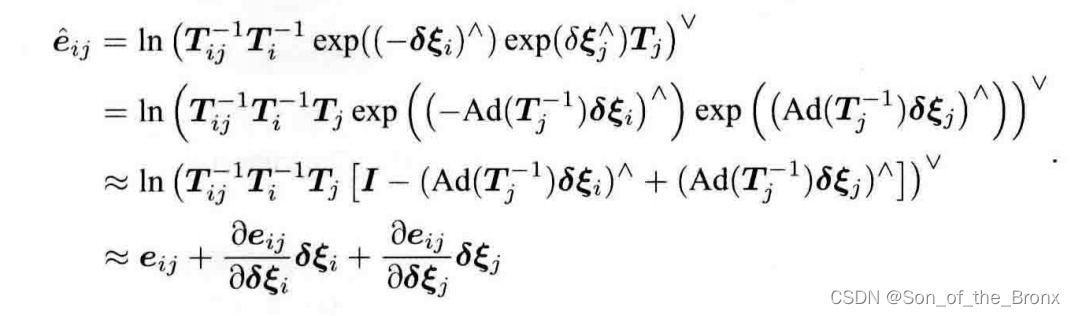
其实对于这个式子我不是很能理解从第三个式子到第四个式子的转变，变换矩阵相加等于李代数的相加？？疑惑

对于上面的一堆公式，我想的是直接从第二个式子展开，忽略了se(3)的BCH近似，结果雅可比跟书上那个是类似的，只不过书上多了一个可以忽略的$J_r$：

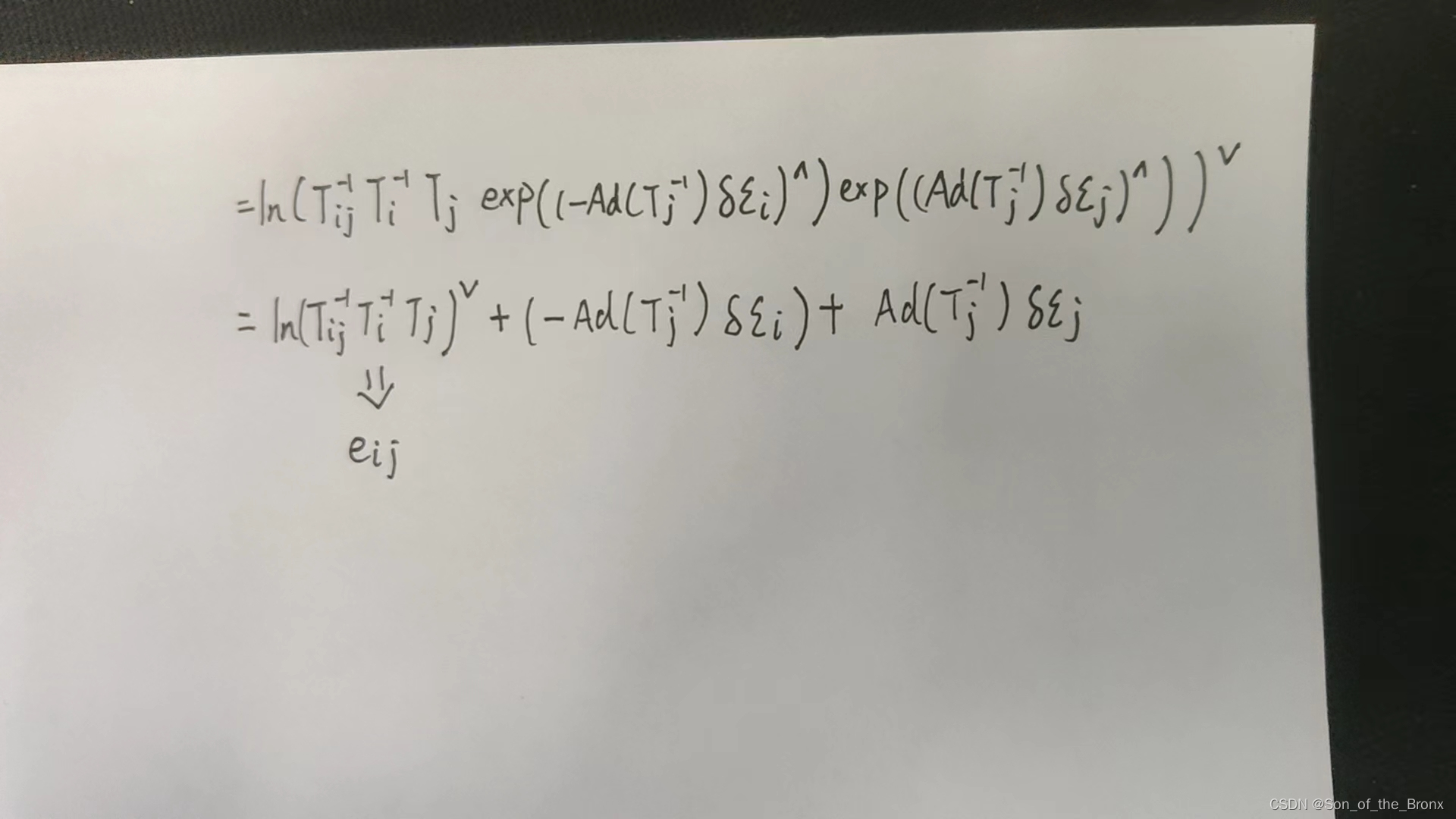
后续的过程就是根据雅可比去求增量方程，求解增量方程优化相机位姿，高斯牛顿的剧情又来了。

基于滑动窗口的后端

这里只考虑滑动窗口BA优化，因为书上对滑动窗口这部分介绍的东西比较少。

个人见解

为什么会想用滑动窗口的方式？就是因为在slam的过程中，图像来了就算一帧，一帧需要优化一个相机位姿和几百个特征点。时间一长，特征点数量就飞速增长，虽然可以采用关键帧的策略，但是关键帧的数量也是会随着slam的过程逐渐增多。所以就产生控制BA规模的想法，最简单的方法就是仅仅保存离当前帧时间最近的N个关键帧，依靠这些关键帧做BA优化。在新增关键帧和关键点的时候是比较好操作的，但是在删除一个旧的关键帧时，就需要边缘化的操作。

旧关键帧的边缘化

具体其实可以参考一篇博客，写的非常清晰：边缘化中矩阵运算的一点细节

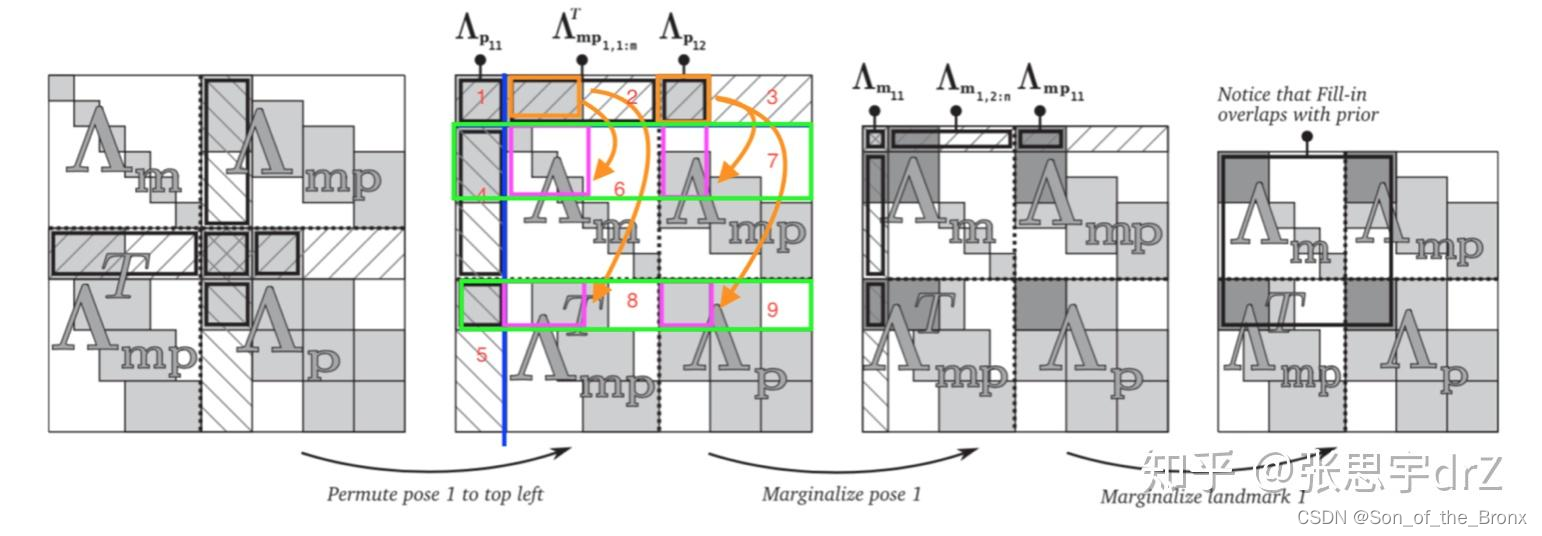
边缘化的过程可以简要的由上面的图片来表示。这个就是整个滑动窗口的BA优化中H矩阵，$A_m$代表的是特征点的部分，$A_p$代表相机位姿的部分。先边缘化相机位姿，这时候有关这个相机位姿的信息就会在schur消元的过程中 Fill-in $A_m$中，然后就是边缘化这个相机位姿的特征点，也是通过schur消元中 Fill-in $A_m$中，但是Fill-in的范围是一致的，不会有新的空白区域被 Fill-in ，最终就可以得到边缘化后的H矩阵。

其实看到最后的H矩阵，$A_m$没法保证自身是对角块矩阵，所以在后续优化求解的时候，就无法通过之前稀疏方式去迭代求解了。这个问题应该也会有一些SLAM框架去解决，采取其他边缘化策略保证$A_m$对角块矩阵的特性。