论文阅读笔记:Equivariant Multi-Modality Image Fusion
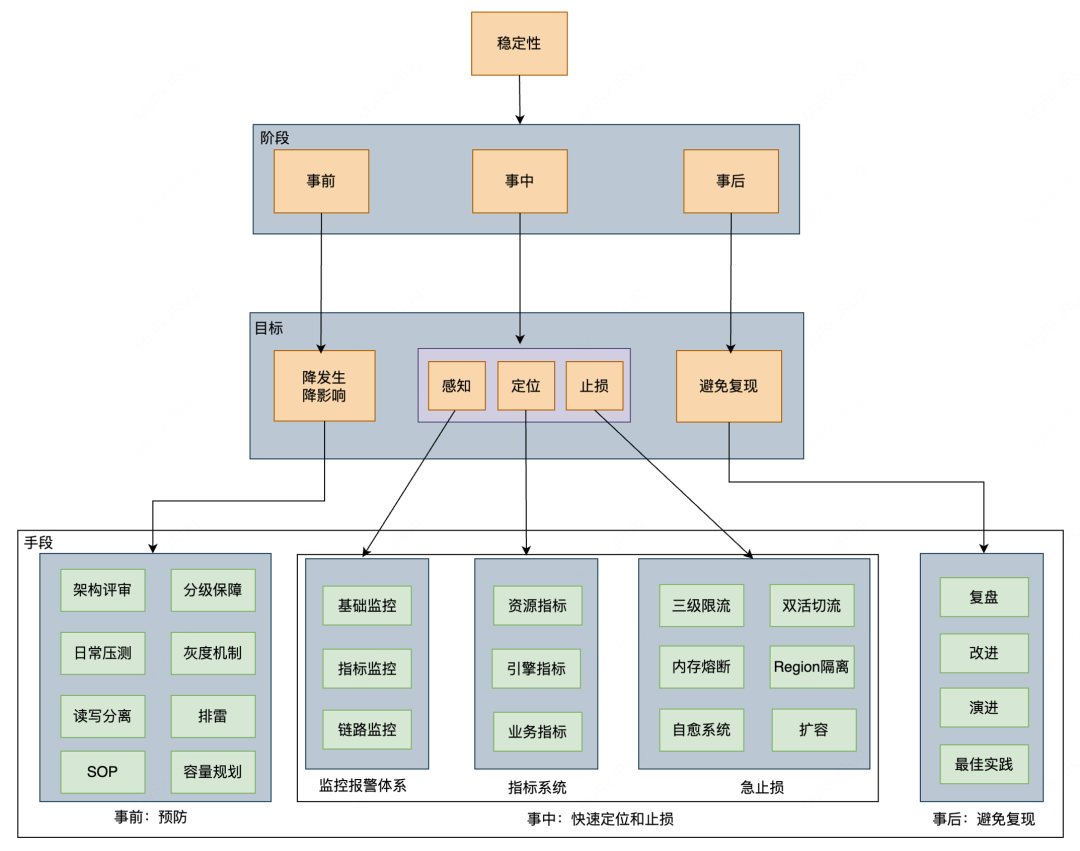
- 1 背景
- 2 创新点
- 3 方法
- 4 模块
- 4.1 模型假设
- 4.2 U-Fuser
- 4.3 伪感知模块
- 4.4 等变图像融合
- 5 实验
- 6 疑问
代码:https://github.com/Zhaozixiang1228/MMIF-EMMA
论文:https://arxiv.org/pdf/2305.11443
1 背景
由于GT融合数据的稀缺性,对融合模型的有效训练具有挑战性。为了解决这个问题,作者提出了端到端自监督学习的等变多模态图像融合( EMMA )范式。本方法是基于自然成像对某些变换的响应是等变的这一先验知识。以此引入了一种新的训练范式,它包含一个融合模块、一个伪感知模块和一个等变融合模块。这些模块使得网络训练在满足先验的同时,还遵循物理感知到成像过程的原理。
多模态图像融合问题可以看成是一个非线性的盲逆问题。可以看成如下的负对数似然最小化问题:

其中
i
1
i_1
i1,
i
2
i_2
i2和
f
f
f分别表示两张输入图像和输出的融合图像。式(1a)为负对数似然,式(1b)基于贝叶斯定理,式(1c)的第一项是数据保真项,表示
i
1
i_1
i1和
i
2
i_2
i2是由
f
f
f感知的,第二项是先验项,表示
f
f
f需要满足一定的融合图像先验。
无数先进的基于深度学习的方法都在努力对这个问题进行更好的建模。然而在这一任务中仍有一些紧迫的问题没有得到解决。对于式(1c)中的第一项,单个传感器仅限于捕获模式特异性特征,不存在能够同时感知所有模态信息的单个超级传感器,就是说没有一个确定的真值去监督模型学习。
另一方面,人工构造的损失函数通常通过最小化L1和L2距离来推动融合图像与源图像相似。然而直接计算来确定融合图像的方法忽略了融合图像和源图像之间潜在的域差异,没有考虑到 f f f和 i 1 i_1 i1, i 2 i_2 i2不在同一个特征流形上。
首先,由于对齐分布和手工构造的损失函数是具有挑战性的任务,所以作者从传感和成像过程入手,目的是学习感知,即从融合图像回到各种模态的图像的逆映射。这种方法比掌握融合过程本身更直观简单。通过这样做,可以衡量输入源图像和(伪)感知结果之间的损失,而(伪)感知结果是通过将融合图像应用于不同的感知函数获得的。该策略克服了没有GT图像进行融合的问题。
自然的成像响应对于诸如位移、旋转和反射等变换是等变的。换句话说,变换后的融合图像,在感知和重新融合后,应该产生与感知前相同的结果。利用自然成像系统的等变性先验,为融合网络内部的学习过程提供了更强的约束和指导。
综上,针对图像融合常用的学习范式,作者做出以下改进:

其中
F
F
F 融合模型,
A
A
A 表示感知模型。
i
1
^
=
A
1
(
f
)
\hat{i_1}=A_1(f)
i1^=A1(f) ,
i
2
^
=
A
2
(
f
)
\hat{i_2}=A_2(f)
i2^=A2(f) 表示
i
1
i_1
i1 和
i
2
i_2
i2 经过相应的感知模型
A
1
A_1
A1
A
2
A_2
A2 的感知结果。
A
1
A_1
A1
A
2
A_2
A2 共同构成了感知模型
A
A
A .
2 创新点
-
提出了一种名为EMMA的新型自监督学习范式,旨在解决图像融合中真值缺失的问题。
-
通过伪感知模块和感知损失分量有效地模拟感知成像过程,改进了传统融合损失中对融合图像和源输入之间域差异的不恰当处理。
-
EMMA中提出的U - Fuser融合模块熟练地建模跨多个尺度的长、短程依赖关系来整合源信息。
-
方法在红外-可见光图像融合和医学图像融合中表现出优异的性能,这也被证明有利于下游的多模态目标检测和语义分割任务。
3 方法
作者将图像融合和感知的过程定义如下:

F
(
⋅
,
⋅
)
F(·,·)
F(⋅,⋅) 表示融合模型,
A
i
A_i
Ai 和
A
v
A_v
Av 表示红外光和可见光图像的感知模型。EMMA工作流如下:

将图像对{ i i i, v v v }作为U - Fuser F F F 的初始输入,得到融合图像 f f f 。接着对 f f f 进行一系列包含平移、旋转、反射等变换 T g T_g Tg,产生 f t f_t ft,然后将 f t f _t ft 输入到参数冻结的{ A i A_i Ai, A v A_v Av }中,生成伪感知图像{ i t i_t it, v t v_t vt },最后输入到 F F F 中,得到重融合图像 f t ^ \hat{f_t} ft^。
与其他方法需要设计良好的损失函数来最小化 f f f 和{ i i i, v v v }之间的距离不同,EMMA的损失侧重于使感知模块从 f f f生成的伪图像{ A i ( f ) , A v ( f ) A_i(f),A_v(f) Ai(f),Av(f) }尽可能接近原始{ i i i, v v v },同时使 f t f_t ft 接近 f t ^ \hat{f_t} ft^。这样,从自然成像的角度出发,找到了最优的融合图像 f f f。
4 模块
4.1 模型假设
为了提供全面的感知和融合模型,作者先提出了一些必要假设:
a) 测量一致性。假设融合函数
F
(
⋅
,
⋅
)
F(·,·)
F(⋅,⋅) 在测量域内保持一致性,即:

然而由于传感过程的不确定性,所以无法通过 A i A_i Ai, A v A_v Av 的逆来求解 F ( i , v ) F(i,v) F(i,v) 。
b) 不变集合一致性。首先给出等变成像中的两个定义:
定义1:不变集合。对于由酉矩阵 T g ∈ R n × n T_g∈R^{n×n} Tg∈Rn×n 组成的变换 G = { g 1 , . . . , g ∣ G ∣ } G=\{g_1, ..., g_{|G|}\} G={g1,...,g∣G∣}, X X X 是和变换g相关的不变集合,如果 ∀ x ∈ X , ∀ g ∈ G , T g x ∈ X ∀x∈X,∀g∈G,T_gx∈X ∀x∈X,∀g∈G,Tgx∈X, 那么 T g X T_gX TgX 和 X X X 相同(就是集合X中的每个元素经过G中的变换还属于集合X,那么X就是不变集合)。
定义2:等变函数。如果函数 I I I 满足 ∀ x ∈ X , ∀ g ∈ G ∀x∈X,∀g∈G ∀x∈X,∀g∈G, I ( T g x ) = T g I ( x ) I(T_gx)=T_gI(x) I(Tgx)=TgI(x),则 I I I 是一个和变换G相关的等变函数。
关于定义1,比如X表示一组自然图像,显然经过平移,旋转后,X还是一组自然图像,因此 X X X 是变换 G G G 的不变集合。融合图像 f f f 作为 X X X 的子集,由融合图像组成的集合也是 G G G 的不变集。此外,在定义1和定义2中,“不变性”指的是数据集的性质,而“等变性”指的是成像系统的性质,即成像系统 F 0 F_0 F0 是关于 G G G 的等变函数。
因此提出以下定理:
定理1(等变图像融合定理):如果将定义2的
I
I
I 看成符合函数 KaTeX parse error: Undefined control sequence: \* at position 2: F\̲*̲A ,其中
F
F
F 是融合模型,
A
A
A 是传感模型,包括
A
i
A_i
Ai 和
A
v
A_v
Av ,则等变图像融合定理为:

证明:考虑一组满足不变性的自然图像
X
X
X,由定义2可知,成像系统 KaTeX parse error: Undefined control sequence: \* at position 2: F\̲*̲A 应等变与变换 {
T
g
T_g
Tg }, 因此 KaTeX parse error: Undefined control sequence: \* at position 7: ∀f∈X,F\̲*̲A(T_gf)=T_gF\*A…, 进一步的将
A
A
A 拆分成
A
i
A_i
Ai 和
A
v
A_v
Av 就可以得到式(5)。
4.2 U-Fuser
作者采用了类似Unet的结构融合
i
i
i 和
v
v
v ,生成融合图像
f
f
f。在每个尺度上,由于输入的跨模态特征既包含环境和背景等全局信息,也包含高亮和细节纹理对象特征等局部特征,因此作者设计了一个Transformer-CNN结构,通过利用的归纳偏差来更好的建模。对于Transformer采用实现了通道维度自注意力机制的Restormer,在不增加过多计算量的情况下队全局特征进行建模。在CNN中采用ResBlock。将Restormer-CNN块的输入特征进行嵌入,然后由Restormer(全局特征)和ResBlock(局部特征)并行处理,接着嵌入交互并输出一个CNN层,最后输入到下个尺度。

4.3 伪感知模块
从了从
A
i
(
f
)
A_i(f)
Ai(f) 和
A
v
(
f
)
A_v(f)
Av(f) 中获得伪成像结果,需要模拟从融合图像中感知红外和可见光的过程,如式(4)(“Ai (F (i, v)) = i, Av (F (i, v)) = v.” (pdf) ) 所述。这个过程无法显示给出,所以作者选择了最先进的15种方法,如CCDFuse等,使用这些方法的融合结果作为融合图像的伪真值,然后学习从融合图像到
i
i
i 和
v
v
v 的映射,分别称为
A
i
A_i
Ai 和
A
v
A_v
Av。作者选择Unet作为
A
i
A_i
Ai 和
A
v
A_v
Av 的骨干网络,如下:

4.4 等变图像融合
在得到U - Fuser F F F 和伪传感函数{ A i A_i Ai, A v A_v Av }之后,就可以搭建基于图像等变先验的自监督学习框架。如图1所示,首先将图像对{ i , v i,v i,v }输入到 F F F 中,得到融合图像 f f f 这是传统融合算法的全部操作。然后,对 f f f 施加一系列变换 T g T_g Tg,包括平移、旋转、反射等,从而得到 f t f_t ft。随后,将 f t f_t ft 输入到训练好的{ A i , A v A_i,A_v Ai,Av }中,得到伪感知图像{ i t , v t i_t,v_t it,vt },它们包含了 f t f_t ft 的信息,分别满足红外和可见光图像的成像特性。最后,将成对的{ i t , v t i_t,v_t it,vt }送入 F F F,得到重建图像 f t ^ \hat{f_t} ft^。在整个框架中,目标是将{ i , v i,v i,v }中的信息聚合成 f f f,并且根据等变图像融合定理(定理1 ), f t f t ft 和 f t ^ \hat{f_t} ft^ 应该足够接近。这些将通过设计的损失函数来保证。
在EMMA的整个训练过程中,首先使用L2损失对 A i A_i Ai, A v A_v Av 进行训练:
L I R e c = L 2 ( i , A i ( f ^ ) ) L_I^{Rec}=L_2(i, A_i(\hat{f})) LIRec=L2(i,Ai(f^))
L
V
R
e
c
=
L
2
(
v
,
A
v
(
f
^
)
)
L_V^{Rec}=L_2(v, A_v(\hat{f}))
LVRec=L2(v,Av(f^))
其中
f
^
\hat{f}
f^ 是SOTA方法的融合图像。然后冻结
A
i
A_i
Ai,
A
v
A_v
Av ,使用总损失来训练U-Fuser模块:

其中
L
(
x
,
x
^
)
=
L
1
(
x
,
x
^
)
+
L
1
(
∇
x
,
∇
x
^
)
L(x,\hat{x})=L_1(x,\hat{x})+L_1(∇x,∇\hat{x})
L(x,x^)=L1(x,x^)+L1(∇x,∇x^) 。始终第一项和第二项保证测量一致性,第三项则保证不变集合一致性假设。
5 实验
图2显示本文方法在融合过程中锐化了纹理,减少了伪影,增强了可视性。

图3中,位于光照不足的环境中,本文方法融合结果的物体具有明确的边缘和丰富的轮廓。

图4中,EMMA在提取结构亮点和细节纹理特征方面表现出更高的准确性,并有效地整合了融合图像中的特征特征。因此,它取得了显著的融合效果。

在可见光红外光融合任务IVF和医学图像融合任务MIF上的指标。(指标计算中只用单张图像计算的指标采用融合后的图像计算,需要两张图像对比计算的指标论文采用的是用融合后的图分别与融合前的图计算指标值,然后取平均为此张融合后图像的指标。)

消融实验:
实验1:移除Loss中的第三项
实验2:将Loss中前两项的改为
L
1
(
f
,
i
)
+
L
1
(
f
,
v
)
L_1(f,i) + L_1(f,v)
L1(f,i)+L1(f,v)
实验3:将Loss直接替换成
L
1
(
f
,
i
)
+
L
1
(
f
,
v
)
L_1(f,i) + L_1(f,v)
L1(f,i)+L1(f,v)
实验4:在实验3的基础上,对
i
i
i 和
v
v
v 做EMMA中相同的数据增广。
实验5:取消U-Fuser中的Global Extractor模块
实验6:取消U-Fuser中的Local Extractor模块

多模态目标检测任务:

多模态分割任务:

6 疑问
感知模型是在可见光和红外光(或者医学图像)上训练的,在其他图像上的泛化性未知。