一、归并排序简介
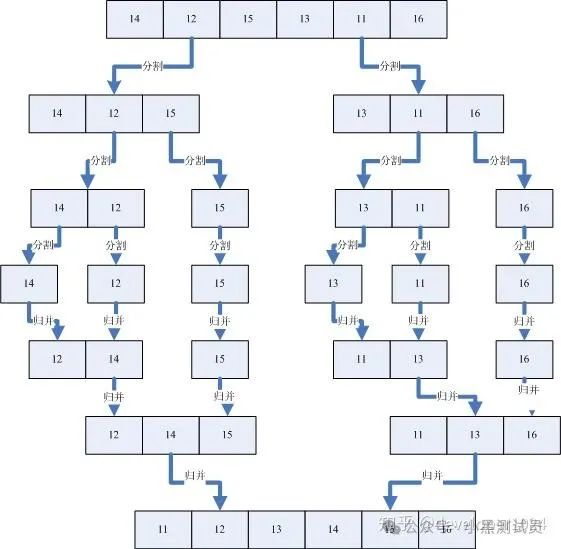
归并排序是一种基于分治策略的有效且稳定的排序算法。归并排序由约翰·冯·诺伊曼提出,是计算机科学中一个非常基础且历史悠久的算法。
归并排序利用分治法的策略,将一个大的数组拆分成几个小的子数组,这些子数组各自独立地排序,然后逐步合并成一个完全有序的大数组。归并排序的时间复杂度为O(n log n),空间复杂度为O(n),其中n是待排序元素的数量。这种算法特别适合于数据量大且对稳定性有要求的排序场景。稳定性指的是相同值的元素在排序前后保持原有的顺序不变。
归并排序的操作过程:
1、递归地将数组分成两半直到每个子数组只包含一个元素。
2、从最小单个元素数组开始合并,创建一个临时数组来存放合并后的结果,设置两个指针分别指向两个子数组的起始位置。比较这两个指针所指的元素,将较小的元素放入临时数组然后删除源数组元素。重复这个过程,直到其中一个数组为空时,将另一数组剩余元素添加到临时数组末尾。
3、回溯并合并将临时数组的内容复制回原数组,完成这一级的合并工作。
特点:归并排序采用的是分治策略,它可以高效地处理大量数据,尤其适用于对稳定性有要求的情况。
二、Python代码实现
# -*- coding: utf-8 -*-
"""
小黑测试员
======================================
File Name :merge_sort.py
Author :lanmingyong
date :2024/5/15 14:39
Description:归并排序是一种基于分治策略的有效且稳定的排序算法。
归并排序利用分治法的策略,将一个大的数组拆分成几个小的子数组,这些子数组各自独立地排序,然后逐步合并成一个完全有序的大数组。归并排序的时间复杂度为O(n log n),空间复杂度为O(n),其中n是待排序元素的数量。
=======================================
"""
def merge_sort(arr):
"""递归方式将数组进行分割,直到数组只有一个元素"""
if len(arr) == 1: # 如果组分割到只剩一个元素时,结束
return arr
mid = len(arr) // 2 # 将数组分成1/2
arr_left = merge_sort(arr[:mid]) # 继续将arr_left数组分成两半
arr_right = merge_sort(arr[mid:]) # 继续将arr_right数组分成两半
return merge(arr_left, arr_right) # 从根根节点开始给两个数组进行排序,并返回排好序的列表
def merge(arr_left, arr_right):
"从左往右遍历两个数组,比较大小,小的放到新数组的第一位,再取小数那一组数组的第二位与第一次比较大的数对比,小的放到新数组的第二位,依次类推"
result_arr = [] # 存放排序好的列表
# 当其中一个数组被取完所有值后,将另一个数量剩余元素放到排序后的数组之后结束循环并返回列表
while True:
if len(arr_left) == 0:
result_arr = result_arr + arr_right
print("每一小组排序结果"+str(result_arr)) # 调试查看每小组排序结果
return result_arr
if len(arr_right) == 0:
result_arr = result_arr + arr_left
print("每一小组排序结果"+str(result_arr)) # 调试查看每小组排序结果
return result_arr
if arr_left[0] > arr_right[0]:
result_arr.append(arr_right[0])
arr_right.pop(0)
else:
result_arr.append(arr_left[0])
arr_left.pop(0)
# 验证
arr = [9, 6, 7, 2, 8, 1, 0, 4, 3,0]
# arr = [89, 65, 21, 8, 76, 79, 0, 86, 51, 33, 34, 8, 76, 53, 93, 88, 65, 0, 92, 56, 76, 9, 0, 54, 9, 37, 94, 72, 92, 72, 88, 44, 34, 48, 14, 22, 76, 34, 45, 50, 66, 4, 77, 41, 64, 24, 65, 99, 16, 64]
print(merge_sort(arr))
# 执行输出
"""
每一小组排序结果[6, 9]
每一小组排序结果[2, 8]
每一小组排序结果[2, 7, 8]
每一小组排序结果[2, 6, 7, 8, 9]
每一小组排序结果[0, 1]
每一小组排序结果[0, 3]
每一小组排序结果[0, 3, 4]
每一小组排序结果[0, 0, 1, 3, 4]
每一小组排序结果[0, 0, 1, 2, 3, 4, 6, 7, 8, 9]
[0, 0, 1, 2, 3, 4, 6, 7, 8, 9]
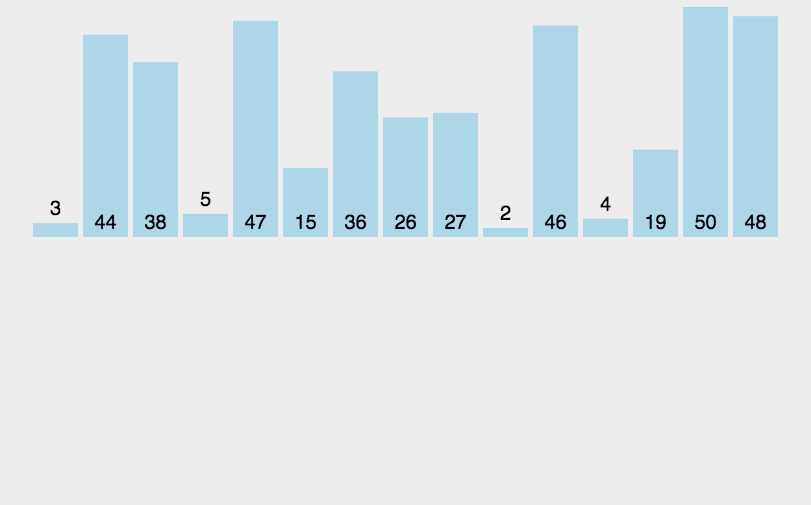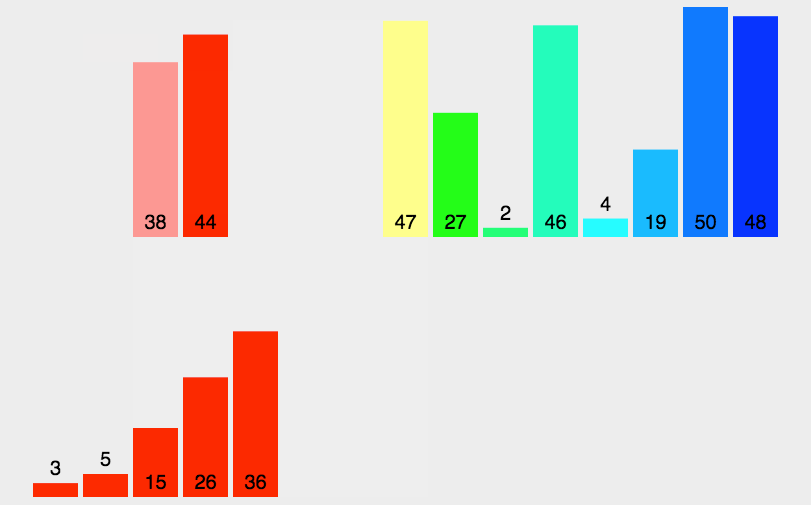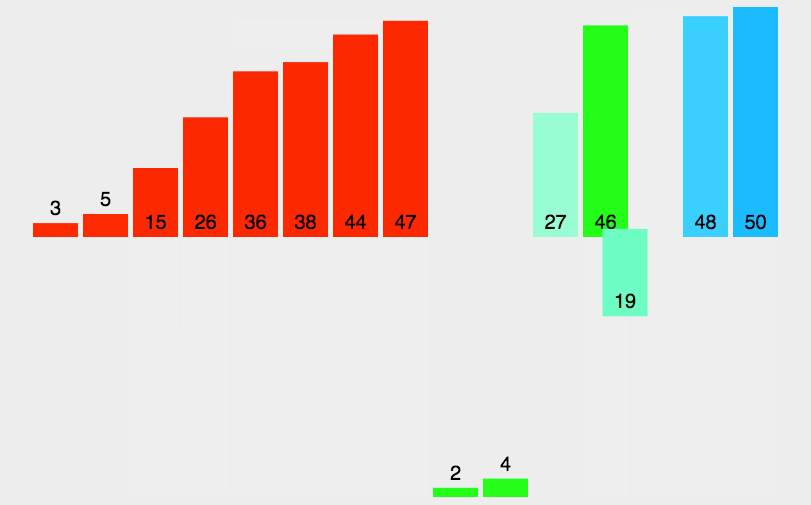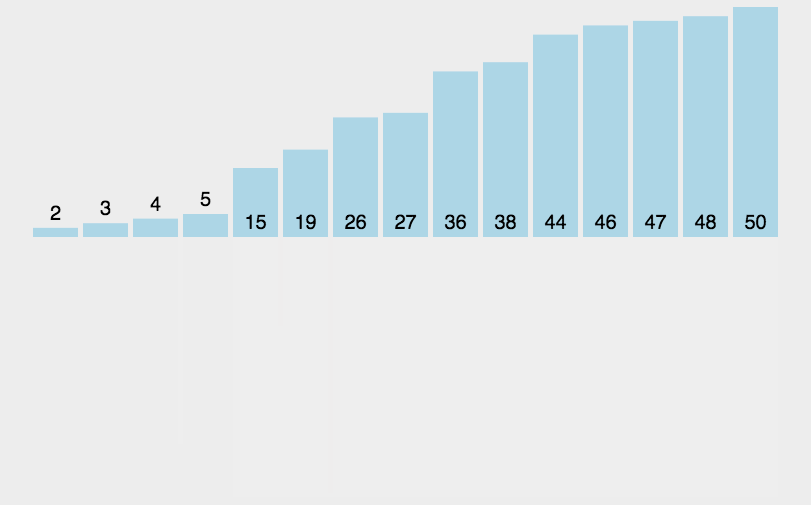
"""三、动画演示
欢迎大家关注我的订阅号,会不定期分享一些相关的文章,有问题也欢迎一起讨论交流学习!