今日任务 

● 哈希表理论基础 
● 242.有效的字母异位词 
● 349. 两个数组的交集 
● 202. 快乐数
● 1. 两数之和   

题目
    大型概括：辅助map +vector(返回值）

方案一：（错误代码没写）

nums1 贡献为 ++

nums2 贡献为   --

最后用nums1为🗡值，遍历到  <=0的，一律添加到vector

没考虑nums2的新元素加入map,也会造成--!!!；

除非只拿nums1作为🗡值去遍历。

方案二：标记法

                nums1 进入map，将数值设置为 2；

              nums2进入map，先检查这里的🗡值是否为2，是的话，改标记为1

    1.题目描述-->思路：

    2.输入 返回值：

    3.边界情况：

    4.时空复杂度：

    5.进一步优化：

利用迭代器！ 

#include <vector>
#include <map>

class Solution {
public:
    std::vector<int> intersection(std::vector<int>& nums1, std::vector<int>& nums2) {
        std::map<int, int> Mymap;
        std::vector<int> qq;
        
        // 标记 nums1 中的元素
        for (int num : nums1) {
            Mymap[num] = 2;
        }
        
        // 找出同时在 nums1 和 nums2 中的元素，并标记为 1
        for (int num : nums2) {
            if (Mymap[num] == 2) {
                Mymap[num] = 1;
            }
        }
        
        // 收集交集结果
        for (auto& pair : Mymap) {
            if (pair.second == 1) {
                qq.push_back(pair.first);
            }
        }
        
        return qq;
    }
};

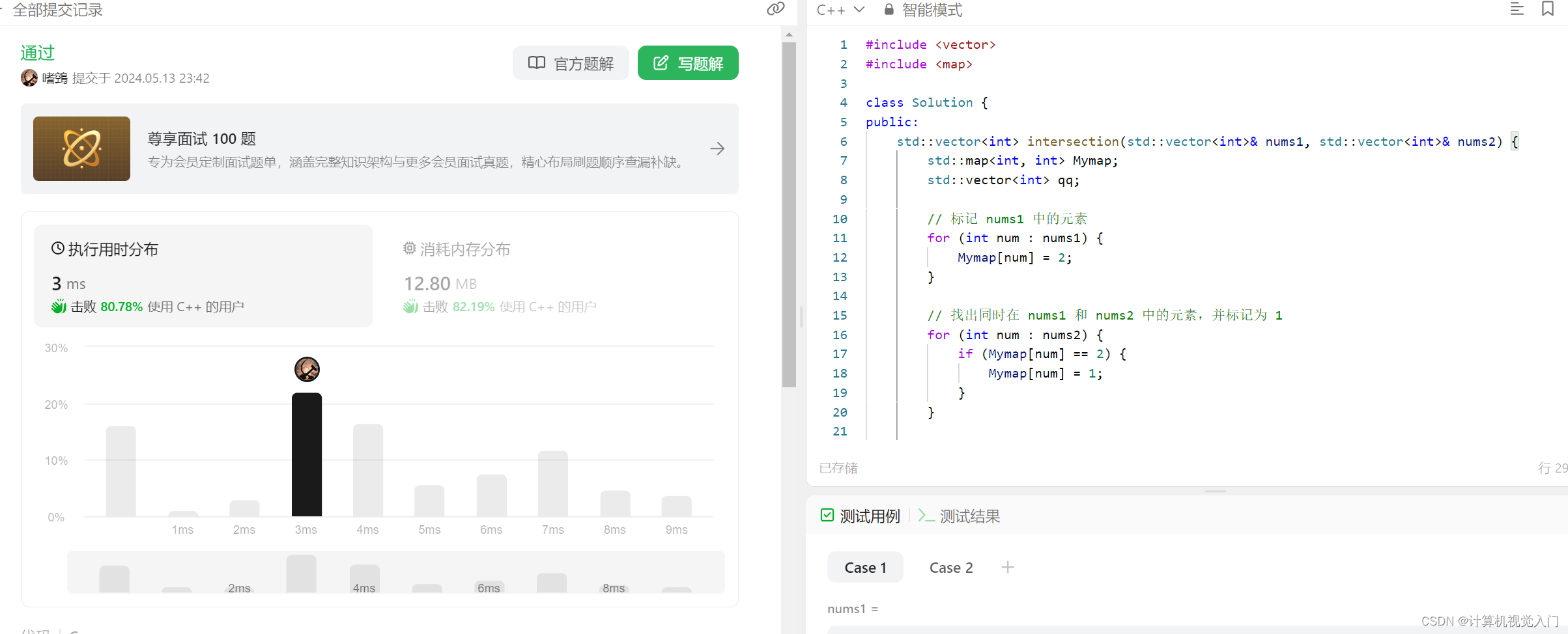
 202. 快乐数 （个人方法，待验证）

题目
    大型概括：方法

  想到了一个证明方法，即缩小问题的规模，问题描述的是2^31-1范围内的数字，其实第一步的计算中（代码中的each），算得最大的数字是 760（Norigin=2XXXXXXX，但是取1999999.。。），第二步的each最大值（由第一步的假设699得到）198。若要成为快乐数，必须要在某一步的计算中，成为1 10 100（不能为1000，因为第一步得到的最大值只有760）。     将原来的题目改成：1-1000（实际为1-760）内的数字 求全部的快乐数。 具体的证明：先求出1-760内全部的快乐数，再测试7步内能得到这样的结果么？ 其实count=7是我 几个数字验证几下出来的，5 6 7； 只要能涵盖1-1000的数字的验证即可。

    1.题目描述-->思路：

    2.输入 返回值：

    3.边界情况：

    4.时空复杂度：

    5.进一步优化：

超时代码：1.虽然考虑无限循环，但是要设置步数

                   思路：内层循环：让每个项都化成 平方累加

                                外层循环，让each = sum，sum=0 进入循环

                                退出：each ==1 

class Solution {
public:
    bool isHappy(int n) {
        int sum =0;
        int each =n;
        int count=0;
        while(each!=1){
            if(count==5)
                return false;
        while(each){
            int a = each%10;
            each = each/10;
            sum+=a*a;
            count++;
        }
        each = sum;
        sum=0;
        }
        return 1;
    }
};

优化方法：

class Solution {
public:
    bool isHappy(int n) {
        int sum;
        int each = n;
        int count = 0;
        
        while (each != 1 && count < 10) { // 修改为 count < 5
            sum = 0; // 重置 sum
            while (each) {
                int a = each % 10;
                each = each / 10;
                sum += a * a;
            }
            each = sum;
            count++;
        }
        
        return each == 1; // 如果 each == 1，返回 true
    }
};

 

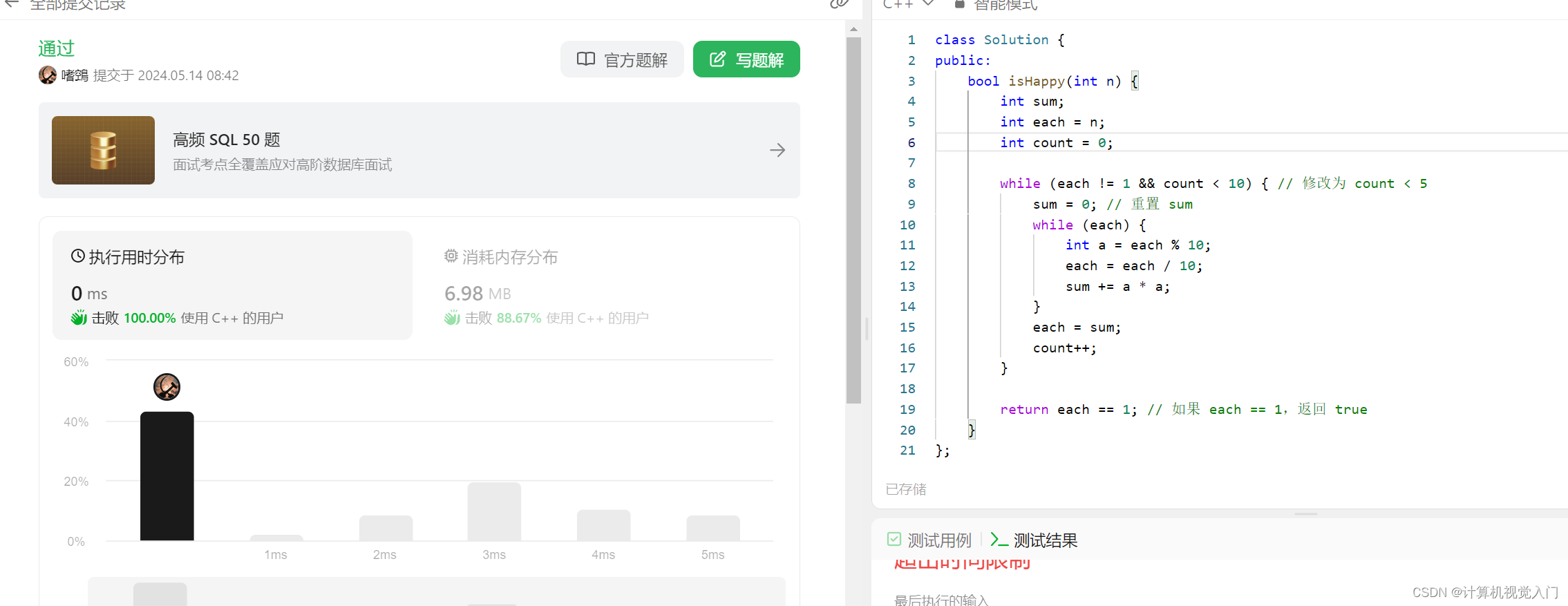
1. 两数之和   （暴力法）

题目
    大型概括：方法

    1.题目描述-->思路：

    2.输入 返回值：

    3.边界情况：

    4.时空复杂度：

    5.进一步优化：纯暴力法，双for

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int size = nums.size();
        vector<int>a;           //辅助
        for(int i=0;i<size-1;i++){
            for(int j=1+i;j<size;j++){
                if(nums[i]+nums[j]==target){
                      a.push_back(i);
                      a.push_back(j);
                      return a;
                }
                    
            }
        }
        return a;
    }
};