我们上次对std中的list进行实现,今天我们要实现stack、queue、priority_queue以及仿函数。
目录
- stack堆
- 堆的框架
- 构造函数
- push插入
- pop删除
- size()大小
- empty()判断空
- top()取栈顶的元素
- queue队列
- 队列框架
- 问题: 这里我们为什么用deque?
- 插入
- 删除
- 取头数据
- 取尾数据
- 判断空和大小
- priority_queue堆
- priority_queue的架构
- empty()判断空
- size()大小
- top()取堆顶元素
- sawp()交换
- push()插入
- pop()删除
- 仿函数
- 仿函数架构
stack堆
堆的原则就是先进后出,后进先出。如图:
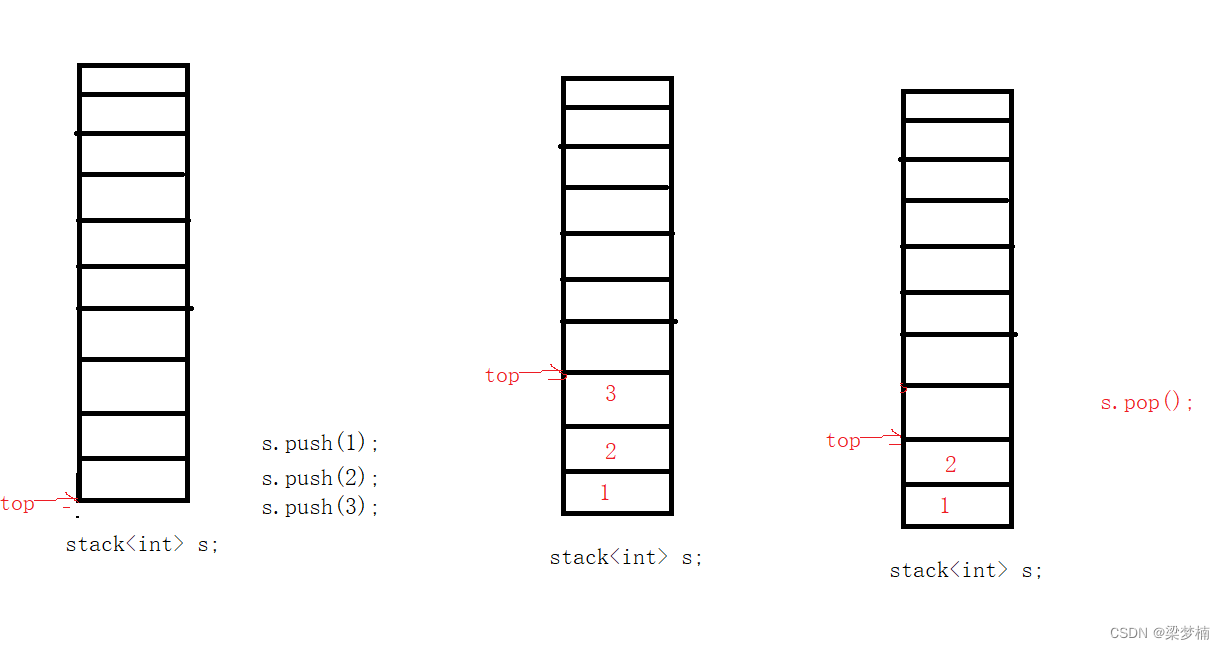
从上图我们可以看出来stack准确说就是一个vector,所以我们就可以利用vector来建。
堆的框架
既然是实现STL库,一定是相似与库中,我们先不看他用的是谁,我们刚刚也分析了用vector来实现,所以我们可以用vector来封装。

这里的Con表示Container(容器),我们只需要传一个容器类型就可以,这里用vector是因为stack的特性,也可以用deque(他是链表与顺序表的结合,这里不会多说)。
template<class T, class Con = vector<T>>
class stack
{
public:
private:
Con _c;
};
构造函数
没错,你没看错,这里我们的构造函数什么都没有写,其实你不写构造函数也可以,我们也说了构造函数对内置类型不做处理,但是对内置类型会去调用它的默认构造,这里我们用了container容器,我们传什么容器类型就是什么容器,我们就可以间接区调用它的构造函数。
stack()
{
}
push插入
push其实很简单,vector中插入数据是不是用的push_back();那么我们可以调用那个成员函数,来达到插入效果。
void push(const T& x)
{
_c.push_back(x);
}
pop删除
pop也是一样的。复用接口。因为我们是后进的先出,所以我们就尾删。
void pop()
{
_c.pop_back();
}
size()大小
size_t size()const
{
return _c.size();
}
empty()判断空
bool empty()const
{
return _c.empty();
}
top()取栈顶的元素
那么什么是栈顶呢?如果数据1的位置是0,那么数据3的位置一定是n-1,所以我们有了size就可以,用size()-1;而且vector支持下标。
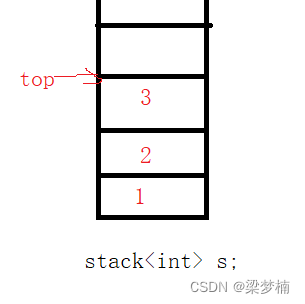
T& top()
{
return _c[size() - 1];
}
queue队列
队列的特性是先进先出,后进后出。
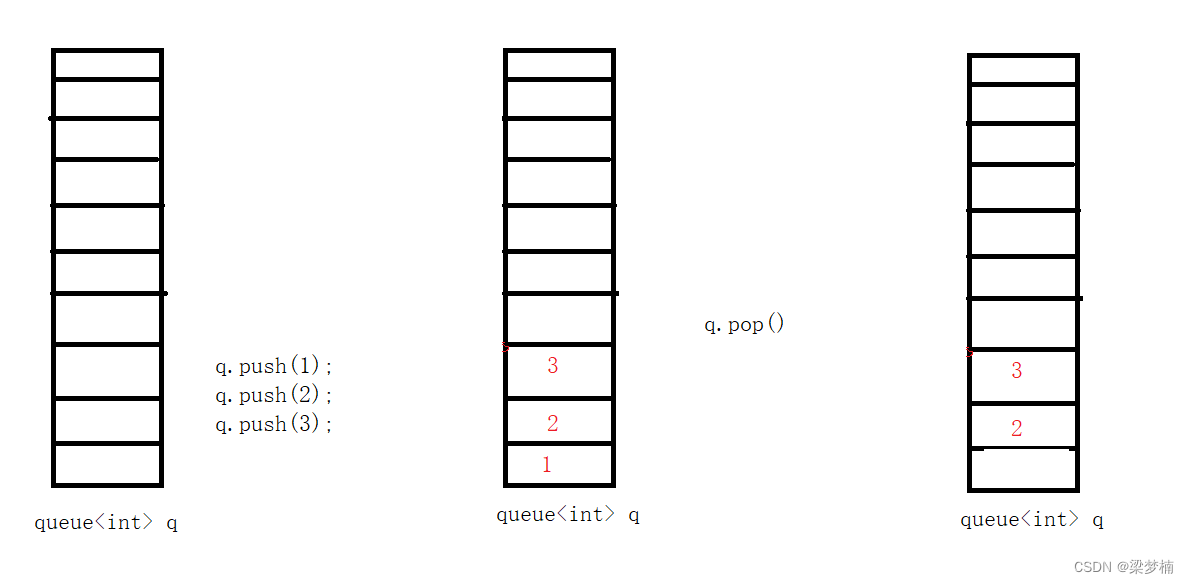
队列框架
其实队列和栈的框架是一样的。
template<class T, class Con = deque<T>>
class queue
{
public:
private:
Con _c;
};
问题: 这里我们为什么用deque?
因为头删问题,我们也知道头删vector是效率很低的,你会说为什么不用list,list不支持下标访问,但是这里用deque就能很好的避免,因为库中deque既有头删,也可以下标访问。
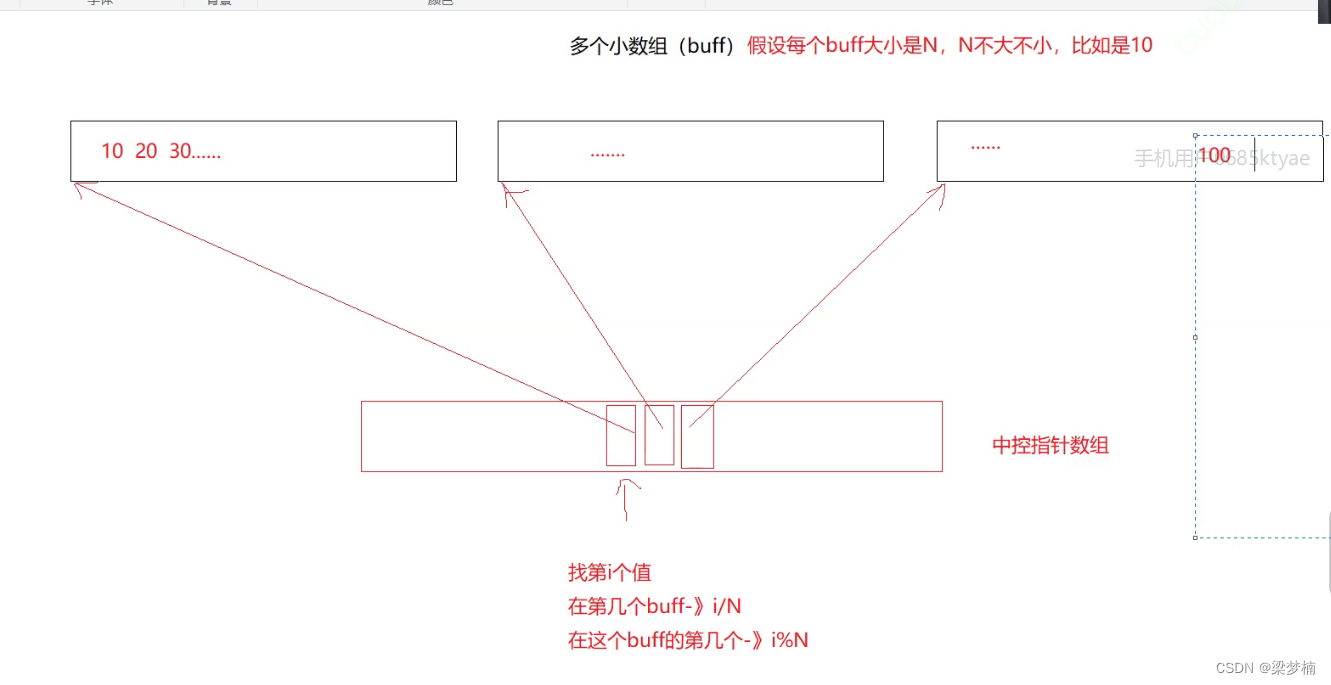
deque的结构其实就是链表和vector的结合。但是deque的缺点也很致命。
- deque的优点
①.头插尾插很快,不需要挪数据,只需要开空间插入
②支持连续访问 - deque的缺点
①.中间的插入删除效率麻烦且一般。
②.方括号的效率并不极致。
插入
void push(const T& x)
{
_c.push_back(x);
}
删除
void pop()
{
_c.pop_front();
}
取头数据
T& front()
{
return _c.front();
}
const T& front()const
{
return _c.front();
}
取尾数据
T& back()
{
return _c.back();
}
const T& back()const
{
return _c.back();
}
判断空和大小
size_t size()const
{
return _c.size();
}
bool empty()const
{
return _c.empty();
}
priority_queue堆
优先级队列和队列没有任何关系!优先级队列是堆,并且他默认是大堆!我们看库中会发现,他和queue共用一个头文件。
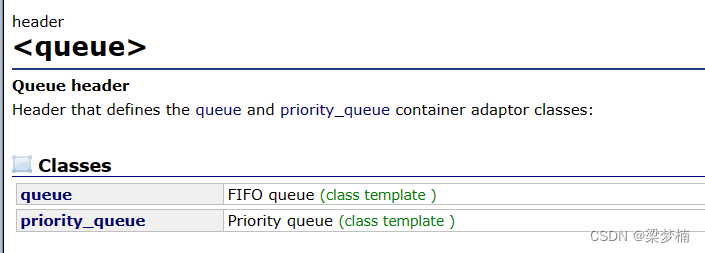
我们在看一下库中的实现。有模板参数有 T、Container、那么Compare是啥啊?我们先不管,看库的时候,遇到不懂得,我们可以先往下看看,如果不影响我们就先不看他,所以我们先排除Compare。先把架子搭出来。

priority_queue的架构
我们还是复用容器类型,堆是完全二叉树,并且之前我们用vector就可以,通过上下调整位置,达到堆。
template<class T ,class Container=vector<T>, class Compare = less<T> >
class priority_queue
{
public:
private:
Container _con;
};

empty()判断空
我们从上图可以看出来priority_queue的成员函数并不多。
bool empty() const
{
return _con.empty();
}
size()大小
size_t size() const
{
return _con.size();
}
top()取堆顶元素
堆顶元素是谁?是不是root根啊,我们用的也是vector,所以堆顶很好取。
T& top()
{
return _con[0];
}
sawp()交换
void swap(T& p1,T&p2)
{
std::swap(p1,p2);
}
push()插入
我们之前学习堆的时候插入是怎么插入的?插到尾部,然后不断向上调整。如图,默认是大堆,我们在尾巴插入一个20,向上调整。通过父子对比,孩子比父亲大,我们就向上调整。
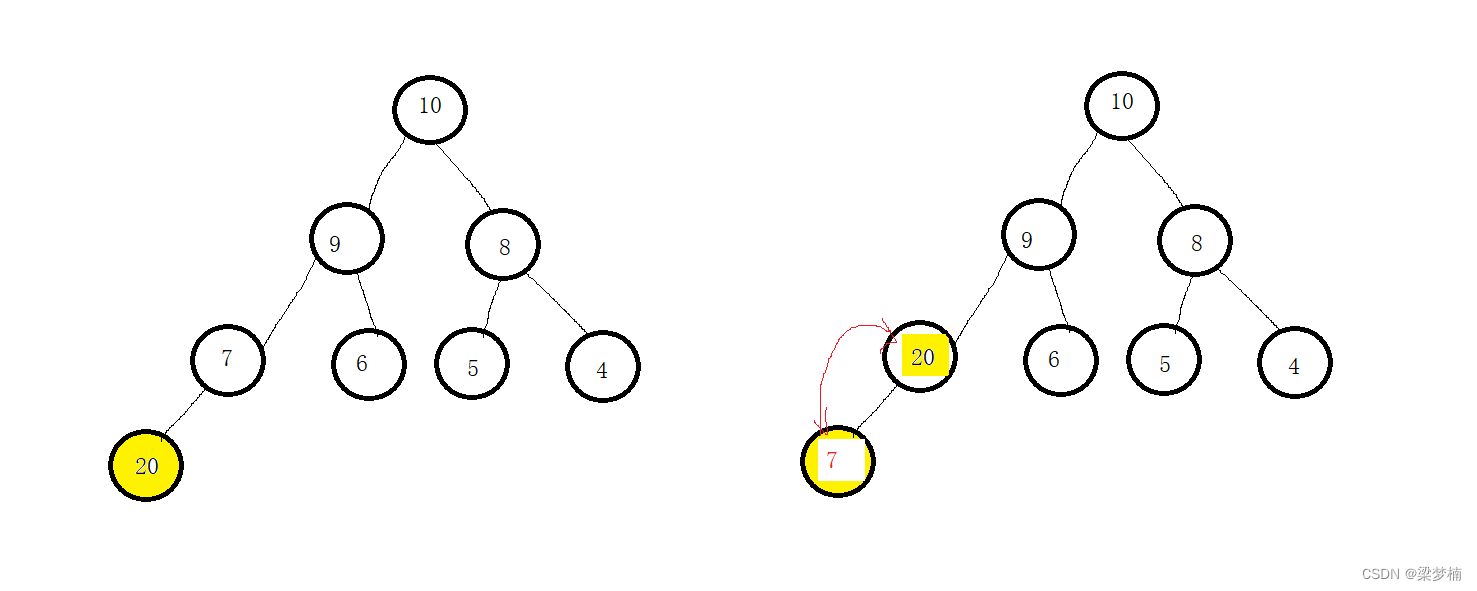
void push(const T& x)
{
//尾插然后向上调整
_con.push_back(x);
AdjustUp(size()-1);
}
void AdjustUp(int child)
{
//Compare c;
int parent = (child - 1) / 2;//找父亲
while (child > 0)
{
//不断调整,直到不满足要求了,结束
//if (_con[child] > _con[parent])
//if (c(_con[parent], _con[child]))
if (_con[parent]<_con[child])
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
pop()删除
库中说从顶部移除元素,所以我们需要删除堆顶。删除堆顶元素,我们可以首尾交换,然后尾删,向下调整。

如图:
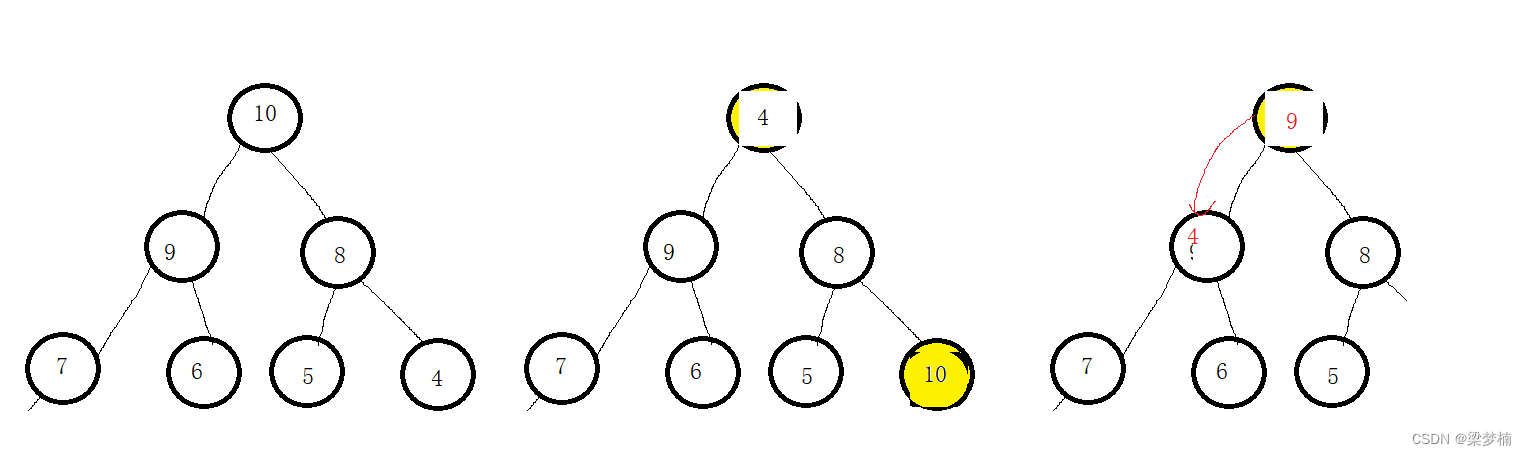
void pop()
{
//头尾交换,删除,然后向下调整
swap(_con[0], _con[size() - 1]);
_con.pop_back();
AdjustDown(0);
}
void AdjustDown(int parent)
{
//Compare c;
int child = parent * 2 + 1;
while (child < size())
{
if (child < size() - 1 && _con[child] < _con[child + 1])
//if (child < size() - 1 && c(_con[child], _con[child + 1]))
{
//这里需要判断一下,因为我们找的都是左子树,判断一下右子树是否存在
//如果存在,在判断一下那个大,哪个大就和哪个换。(默认大堆)
child++;
}
if (_con[parent] < _con[child])
//if (c(_con[parent], _con[child]))
{
swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
仿函数
上述我们只能实现默认的大堆,现在如果我希望你实现一个小堆,你怎么办?ok,你会说我修改一下大于小于号,那么如果在实战的项目中,让你实现,你会和客户说等我一下,我修改一下大于小于号?那不可能,那怎么做呢?仿函数!
其实我们也见过仿函数,在排序中,我们可以利用仿函数排升序降序。

如果你在C语言阶段用过排序qsort();里面是不是会让你们传一个函数指针类型?其实仿函数就是解决了回调函数问题(函数指针)。
仿函数架构
其实在我们上面写priority_queue的时候,你会发现默认给的less却是大堆,这个我也不知道为什么,记住就好了。其实仿函数,你可以理解为,只要重载了operator() 就算是仿函数。
你看输出的时候,是不是特别像一个函数?其实并不是的,其实只是重载了小括号。
template<class T>
class less
{
//控制大堆
public:
bool operator()( const T& x,const T&y)
{
return x < y;
}
};
template<class T>
class greater
{
//控制小堆
public:
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
template<class T ,class Container=vector<T>, class Compare = less<T> >
class priority_queue
{
public:
void push(const T& x)
{
//尾插然后向上调整
_con.push_back(x);
AdjustUp(size()-1);
}
void pop()
{
//头尾交换,删除,然后向下调整
swap(_con[0], _con[size() - 1]);
_con.pop_back();
AdjustDown(0);
}
private:
void AdjustDown(int parent)
{
Compare c;
int child = parent * 2 + 1;
while (child < size())
{
//if (child < size() - 1 && _con[child] < _con[child + 1])
if (child < size() - 1 && c(_con[child], _con[child + 1]))
{
child++;
}
//if (_con[parent] < _con[child])
if (c(_con[parent], _con[child]))
{
swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void AdjustUp(int child)
{
Compare c;//创建比较的对象
int parent = (child - 1) / 2;
while (child > 0)
{
//if (_con[child] > _con[parent])
//if (_con[parent]<_con[child])
if (c(_con[parent], _con[child]))//传哪个仿函数调哪个
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
Container _con;
};