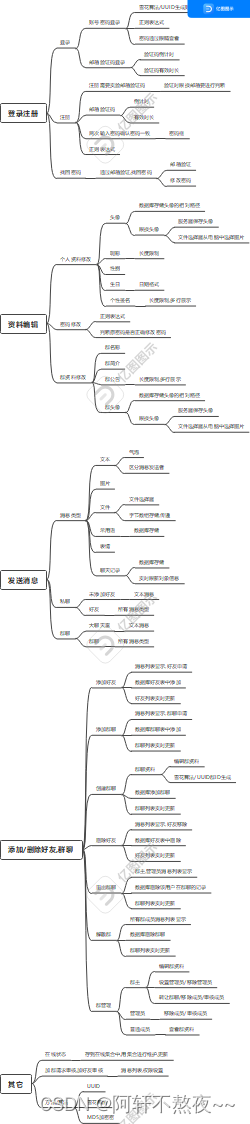
比赛记录:看群里大家嘎嘎拿牌,自己个人来solo了一下,发现简单到中等题很多,写了两小时出了7题,但是写的比较慢,对难题把握还是不准确
![]()
补题 : A题确实巧妙充分利用题目的数据范围来思考问题,D简单数数性质推理
A.Once In My Life
数理逻辑推理
题目要求我们构造奇怪的式子得满足出现123456789 + 一个指定的数,给定n要求找到一个k使得n*k符合要求,同时告诉我们 n < 1e8,k<2e10,可以注意到两者的乘积是刚好到达上限1e18级别那么我们如何去思考:我们无非就是想找到一个符合要求的数(1e18)同时是n的倍数->推出k,依照数据范围我们应该是在时间求出答案,我们看如何得到这个数,可以看到1234567890 + d是10位数 后面还可以接上8位数,也就是说这个 + 与n同级别数是可以构造出来的,那么构造完成之后加上快要变成n倍数的余数就是n的倍数了
void solve(){
LL n,d; cin>>n>>d;
LL ans = 1234567890 + d;
LL x=n;
while(x){
x/=10;
ans *= 10;
}
ans += (n-ans%n)%n;
cout << ans/n << endl;
return ;
}B.扫雷1
贪心
我们是从前往后走的,可以得到如果要选择当前这个数必然是因为后面的点都小于等于这个数,否则我直接买后面的更优,所以我们只需要预处理出来后缀最小值即可
int w[N],suf[N];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>w[i];
suf[n+1]=2e9;
for(int i=n;i>=1;i--) suf[i]=min(suf[i+1],w[i]);
int ans=0,cnt=0;
for(int i=1;i<=n;i++){
ans++;
if(ans>=w[i]){
if(w[i]<=suf[i+1]){
cnt += ans/w[i];
ans %= w[i];
}
}
}
cout << cnt << endl;
return ;
}D.距离之比
数学推理
我们可以对题目中式子进行推理之后就是两个点之间的横纵坐标构成的三角形的的三角函数之比
我们对这个式子研究单调性之后可以得出结论实在45度或者135度的时候结果是最优的所以我们分别按照 x + y 和 x - y排序之后求解相邻两个点的结果即可
PII e[N];
bool cmp1(PII a,PII b){
return a.x+a.y<b.x+b.y;
}
bool cmp2(PII a,PII b){
return a.x-a.y<b.x-b.y;
}
double get(PII a,PII b){
double dx = abs(a.x-b.x),dy = abs(a.y - b.y);
return 1.0*(dx+dy)/sqrtl((dx*dx+dy*dy));
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++){
int x,y; cin>>x>>y;
e[i]={x,y};
}
sort(e+1,e+1+n,cmp1);
double ans = 0;
for(int i=1;i<=n;i++){
int last = i==1 ? n : i-1;
double now =get(e[i],e[last]);
ans = max(ans,now);
}
sort(e+1,e+1+n,cmp2);
for(int i=1;i<=n;i++){
int last = i==1 ? n : i-1;
double now =get(e[i],e[last]);
ans = max(ans,now);
}
cout << LF(11) << ans << endl;
return ;
}F.优秀字符串
签到模拟
直接按照题目意思要操作即可
void solve(){
cin>>n;
int ans = 0;
while(n--){
string s; cin>>s;
if(s.size()!=5) continue;
s=' '+s;
set<char> S;
for(int i=1;i<=4;i++) S.insert(s[i]);
if(S.size()!=4) continue;
if(s[3]!=s[5]) continue;
ans ++ ;
}
cout << ans << endl;
return ;
}H.随机栈
模拟+概率
要求我们得到的是递增的序列,那么我们取出来的数一定是当前集合最小的数才有可能,同时取出来的数的概率为 ,用快速幂求逆元,维护集合最小值可以用优先队列,数量开个桶即可
LL qmi(LL a,LL b,LL p){
LL res = 1;
while(b){
if(b&1) res=res*a%p;
b>>=1;
a=a*a%p;
}
return res;
}
LL inv(LL x){
return qmi(x,mod-2,mod);
}
void solve(){
cin>>n;
priority_queue<int,vector<int>,greater<int>> q;
vector<int> cnt(N);
LL ans = 1;
for(int i=1;i<=2*n;i++){
int x; cin>>x;
if(x!=-1) q.push(x),cnt[x]++;
else{
int x = q.top();
ans *= (LL)cnt[x]*qmi((int)q.size(),mod-2,mod)%mod;
ans %= mod;
ans = (ans+mod)%mod;
a.push_back(x); q.pop();
cnt[x]--;
}
}
int last = -1;
bool ok = true;
for(auto&v:a){
if(v>=last) last=v;
else{
ok = false; break;
}
}
if(!ok){
cout << 0 << endl;
return ;
}
ans = (ans%mod+mod)%mod;
cout << ans << endl;
return ;
}J.排列和组合
暴力 or 小推理
做法1:我们可以发现测试数据不多,我们可以直接跑出全排列即可,可以用素数筛跑出来当前这个数是不是合数
做法2:以0,2,4,5,6,8结尾的一定是合数,由于歌巢原理这六个数至少会出现一个,调整到最后位置即可
int p[N];
bool st[N];
int cnt;
void get(){
for(int i=2;i<N;i++){
if(!st[i]) p[cnt++]=i;
for(int j=0;p[j]<N/i;j++){
st[i*p[j]]=true;
if(i%p[j]==0) break;
}
}
}
void solve(){
int n = 5;
int x; cin>>x;
for(int i=1;i<=n;i++) p[i]=x%10,x/=10;
sort(p+1,p+1+n);
do{
int now = 0;
for(int i=1;i<=n;i++) now = now*10+p[i];
if(now<10000) continue;
if(st[now]){
cout << now << endl;
return ;
}
}while(next_permutation(p+1,p+1+n));
return ;
}K.树上问题
树形dp
我们首先把1当成根来处理可以发现每一次换根节点只会影响当前这一条边,做个简单树形dp转移即可
vector<int> g[N];
int dp[N];
void dfs1(int u,int fa){
dp[u]= (2*a[u]>=a[fa]);
for(auto&v:g[u]){
if(v==fa) continue;
dfs1(v,u);
dp[u] += dp[v];
}
}
void dfs2(int u,int fa){
if(u!=1) dp[u] = dp[fa] - (2*a[u]>=a[fa]) + (2*a[fa]>=a[u]);
for(auto&v:g[u]){
if(v==fa) continue;
dfs2(v,u);
}
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++) g[i].clear(),dp[i]=0;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<n;i++){
int a,b; cin>>a>>b;
g[a].push_back(b);
g[b].push_back(a);
}
dfs1(1,0);
dfs2(1,0);
int ans = 0;
for(int i=1;i<=n;i++) ans += dp[i]==n;
cout << ans << endl;
return ;
}L.Toxel 与 PCPC II
dp处理
我们可以发现对于当前点一定就是从前面几个点转移过来的,也就是说从上一次的最优情况到当前我和前面那几个一起,我们发现由于很大,所以转移的次数不是很大简单论证一下就是n开四次方即可,我们可以处理到30,这样我们来定义dp[i][j]为当前处理到第i个数,处理第i个的时候是一次性处理j个以前debug的,时间复杂度就是30n
LL dp[N][32];
LL d[N];
void solve(){
cin>>n>>m;
for(int i=1;i<=m;i++) cin>>a[i];
for(int i=1;i<=m;i++){
d[i]=2e18;
for(int j=1;j<=i and j<=30;j++){
dp[i][j]=d[i-j]+a[i]+(LL)j*j*j*j;
d[i]=min(d[i],dp[i][j]);
}
}
cout << d[m] << endl;
return ;
}M.有效算法
二分
依照题目意思我们发现明显的具有二分性质,接下来思考如何check我们直接依照式子推导可以得到
对于每一个a,b可以得到一个区间,也就是所有的区间要有一个交点即可,也就是最大的右端点要小于最小的左端点
LL a[N],b[N];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
auto check = [&](LL k){
LL l=-2e18,r=2e18;
for(int i=1;i<=n;i++){
l=max(l,a[i]-k*b[i]);
r=min(r,a[i]+k*b[i]);
}
return l<=r;
};
LL l = 0 ,r = 1e9;
while(l<r){
LL mid = l+r>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
cout << l << endl;
return ;
}