经典神经网络(8)GAN、CGAN、DCGAN、LSGAN及其在MNIST数据集上的应用
1 GAN的简述及其在MNIST数据集上的应用
- GAN模型主导了生成式建模的
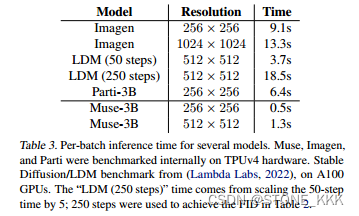
前一个时代,但由于训练过程中的不稳定性,对GAN进行扩展需要仔细调整网络结构和训练考虑,因此GANs虽然在为单个或多个对象类别建模方面表现出色,但扩展到复杂的数据集上,非常具有挑战性。 - 最近几年发布的一系列大型模型,如DALL-E系列、Imagen、Parti和Stable Diffusion,开创了图像生成的新时代,在
图像质量和模型灵活性方面达到了前所未有的水平。 - 目前占主导地位的范式
扩散模型和自回归模型,都依赖于迭代推理这把双刃剑,因为迭代方法能够以简单的目标进行稳定的训练,但在推理过程中会产生更高的计算成本。与此形成对比的是生成对抗网络(GAN),只需要一次forward pass即可生成图像,因此本质上是更高效的。 - 虽然现在超大型的模型、数据和计算资源都主要集中在扩散模型和自回归模型上。但是,也有研究人员证明GAN仍然是文本生成图像的可行选择之一,例如:2023年提出的GigaGAN(https://arxiv.org/abs/2303.05511)。
- 今天,我们来了解下生成式对抗网络GAN及其几个改进网络。
1.1 GAN的简述
- GAN 是
Generative Adversarial Network 生成式对抗网络英文的缩写,由蒙特利尔大学的Ian Goodfellow在2014年提出。 - GAN由两个部分组成:
- 一个是生成器Generator,尽量去学习真实的数据分布,随机接收一个随机噪声来生成无限接近真实数据的图像。
- 一个是鉴别器Discriminator,判断一张图像是不是“真实的”,输入是一张图像,输出是该图像为真实图像的概率,介于0-1之间,概率值越小认为生成图像不真实的可能性越大。
- 生成器的目标是通过生成接近真实的图像来欺骗判别器,而判别器的目标是尽量辨别出生成器生成的假图像和真实图像的区别。生成器希望假图像更逼真判别概率高,而判别器希望假图像再逼真也可以判别概率低,通过这样的动态博弈过程,最终达到
纳什均衡点,通过深度神经网络训练完成之后,生成器可以从一段随机数中生成逼真的图像。 - 不过,GAN存在着训练困难、生成器和判别器的loss无法指示训练进程、生成样本缺乏多样性等问题,因此出现了一系列改进模型,如:CGAN、LSGAN、DCGAN、WGAN、WGAN-GP、BEGAN、CycleGAN等。
- 论文链接:https://arxiv.org/pdf/1406.2661.pdf
1.1.1 GAN的架构

- 生成器G:尽量去学习真实的数据分布,生成无限接近真实数据的样本
- 判别器D:尽量去判别输入数据是真实数据还是来自于生成器生成的数据
- 主要过程为:
- 输入噪声(隐藏变量)z
- 通过生成部分G,得到 G ( z ) = x f a k e G(z)=x_{fake} G(z)=xfake
- 从真实数据集中取一部分真实数据 x r e a l x_{real} xreal
- 将两者混合 x = x f a k e + x r e a l x=x_{fake}+x_{real} x=xfake+xreal
- 将数据喂入判别部分D,给定标签 l a b e l f a k e = 0 , l a b e l r e a l = 1 label_{fake}=0,label_{real}=1 labelfake=0,labelreal=1(简单的二类分类器)
- 按照分类结果,回传loss
- GAN的对抗生成思想主要由其目标函数实现,通过给定一个生成器G和一个判别器D,GAN的目标函数 V ( G , D ) V(G, D) V(G,D)具体公式如下所示:

我们可以分两部分开看这个公式,即判别器最大化与生成器最小化。
在判别器角度,我们希望最大化这个目标函数
- 因为在公式的第一部分,其表示GT样本 ( x ~ p d a t a ) (x~p_{data}) (x~pdata)输入判别器后输出的置信度,当然是越接近1越好。
- 而公式的第二部分表示生成器输出的生成样本 G ( z ) G(z) G(z)再输入判别器中进行进行二分类判别,因为 l o g ( 1 − D ( G ( z ) ) ) < = 0 log(1-D(G(z)))<=0 log(1−D(G(z)))<=0,那么输出的置信度当然是越接近0越好,所以 1 − D ( G ( z ) ) 1-D(G(z)) 1−D(G(z))越接近1越好。
在生成器角度,我们希望最小化【判别器目标函数的最大值】
- 判别器目标函数的最大值代表的
是真实数据分布与生成数据分布的JS散度 - JS散度可以度量分布的相似性,两个分布越接近,JS散度越小(JS散度是在初始GAN论文中被提出,实际应用中会发现有不足的地方,后来的论文陆续提出了很多的新损失函数来进行优化)。
生成器与判别器之间存在着对抗
- 一方面,从生成器而言,希望 D ( G ( z ) ) D(G(z)) D(G(z))为1,提高自己的生成能力;
- 另一方面,从判别器而言,希望 D ( G ( z ) ) D(G(z)) D(G(z))为0,提高自己的判别能力。
- 作者经过理论证明,两者最终可以达到
纳什均衡——处于此状态下,利益达到最大,双方都不愿意改变自己的状态。
1.1.2 理论证明
作者在论文中,证明了生成器与判别器最终可以达到纳什均衡状态。证明的过程中,利用了KL散度的概念,KL散度可以参考:信息量、熵、KL散度、交叉熵概念理解。
-
首先,我们在
给定生成器的情况下,考虑最优化判别器D。和一般的基于Sigmoid的二分类模型训练一样,训练判别器D也是最小化交叉熵的过程,其损失函数为(二分类):
O b j D ( θ D , θ G ) = − 1 2 E x ~ p d a t a ( x ) [ l o g D ( x ) ] − 1 2 E z ~ p z ( z ) [ l o g ( 1 − D ( g ( z ) ) ] Obj^D(\theta_D,\theta_G)=-\frac{1}{2}E_{x~p_{data}}(x)[logD(x)]-\frac{1}{2}E_{z~p_{z}(z)}[log(1-D(g(z))] ObjD(θD,θG)=−21Ex~pdata(x)[logD(x)]−21Ez~pz(z)[log(1−D(g(z))] -
训练过程就是最小化损失函数的过程,在连续空间上我们进而写成
O b j D ( θ D , θ G ) = − 1 2 ∫ x p d a t a ( x ) l o g D ( x ) − 1 2 ∫ z p z ( z ) l o g ( 1 − D ( g ( z ) ) 我们考虑在优化 D 的时候 G 是不变的,并且假设,通过 G 生成的 g ( z ) 满足的分布为 p g ,因此上式改写为: = − 1 2 ∫ x [ p d a t a ( x ) l o g D ( x ) + p g ( x ) l o g ( 1 − D ( x ) ) ] Obj^D(\theta_D,\theta_G)=-\frac{1}{2}\int_xp_{data}(x)logD(x)-\frac{1}{2}\int_zp_{z}(z)log(1-D(g(z))\\ 我们考虑在优化D的时候G是不变的,并且假设,通过G生成的g(z)满足的分布为p_g,因此上式改写为: \\ =-\frac{1}{2}\int_x[p_{data}(x)logD(x)+p_{g}(x)log(1-D(x))] \\ ObjD(θD,θG)=−21∫xpdata(x)logD(x)−21∫zpz(z)log(1−D(g(z))我们考虑在优化D的时候G是不变的,并且假设,通过G生成的g(z)满足的分布为pg,因此上式改写为:=−21∫x[pdata(x)logD(x)+pg(x)log(1−D(x))]
- 去除常量-1/2,我们约定质量函数为 V ( G , D ) V(G,D) V(G,D)
V ( G , D ) = E x ~ p d a t a ( x ) [ l o g D ( x ) ] − E z ~ p z ( z ) [ l o g ( 1 − D ( g ( z ) ) ] = ∫ x [ p d a t a ( x ) l o g D ( x ) + p g ( x ) l o g ( 1 − D ( x ) ) ] 上式什么时候取最大呢? a l o g ( y ) + b l o g ( 1 − y ) 在 [ 0 , 1 ] 上当 y = a a + b 取最大值,因此上式取得最大值时: D G ∗ ( x ) = p d a t a p d a t a + p g ( x ) , 此即为判别器的最优解 V(G,D)=E_{x~p_{data}}(x)[logD(x)]-E_{z~p_{z}(z)}[log(1-D(g(z))]\\ =\int_x[p_{data}(x)logD(x)+p_{g}(x)log(1-D(x))] \\ 上式什么时候取最大呢?\\ alog(y)+blog(1-y)在[0,1]上当y=\frac{a}{a+b}取最大值,因此上式取得最大值时:\\ D^*_{G}(x)=\frac{p_{data}}{p_{data}+p_{g}(x)},此即为判别器的最优解 V(G,D)=Ex~pdata(x)[logD(x)]−Ez~pz(z)[log(1−D(g(z))]=∫x[pdata(x)logD(x)+pg(x)log(1−D(x))]上式什么时候取最大呢?alog(y)+blog(1−y)在[0,1]上当y=a+ba取最大值,因此上式取得最大值时:DG∗(x)=pdata+pg(x)pdata,此即为判别器的最优解
-
我们将判别器的最优解,代入到质量函数 V ( G , D ) V(G,D) V(G,D)中

-
KL散度是非负的,所以我们可以认为-log4是最小值
-
为了证明 p d a t a = p g p_{data}=p_g pdata=pg是使上式取-log4的唯一点,这里可以使用JS散度的特性
-

-
因此,当且仅当 p d a t a = p g p_{data}=p_g pdata=pg,我们得到最优生成器,即生成器的概率密度函数等于真实数据的概率密度函数,也即生成的数据和真实数据是一样的;
-
此时最优判别器 D ∗ = 1 2 D^*=\frac{1}{2} D∗=21,即判别器无法判断数据到底是来自真实样本,还是伪造的数据。
-
1.1.3 模型的训练过程
先训练判别器使判别器达到最优,再训练生成器使二者完成对抗优化,最终达到 p d a t a = p g p_{data}=p_g pdata=pg

如上图所示,生成对抗网络会训练并更新判别分布(即 D,蓝色的虚线),更新判别器后就能将数据真实分布(黑点组成的线)从生成分布(绿色实线)中判别出来。
下方的水平线代表采样域Z,其中等距线表示Z中的样本为均匀分布,上方的水平线代表真实数据X中的一部分。向上的箭头表示映射 x = G ( z ) x=G(z) x=G(z) 如何对噪声样本(均匀采样)施加一个不均匀的分布 p g p_g pg.
- 在算法内部循环中训练 D 以从数据中判别出真实样本,该循环最终会收敛到
D G ∗ ( x ) = p d a t a p d a t a + p g ( x ) D^*_{G}(x)=\frac{p_{data}}{p_{data}+p_{g}(x)} DG∗(x)=pdata+pg(x)pdata
- 随后固定判别器并训练生成器,在更新G之后,D的梯度会引导 G ( z ) G(z) G(z)流向更可能D分类为真实数据的方向。
- 经过若干次训练后,如果G和D有足够的复杂度,那么它们就会到达一个均衡点,这个时候 p d a t a = p g p_{data}=p_g pdata=pg。
1.1.4 GAN存在的问题
1、可解释性非常差
- 所学到的数据分布,没有显示的表达式。
- 它只是一个黑盒子一样的映射函数: 输入是一个随机变量,输出想要的一个数据分布。
2、训练不稳定
- 难以保持生成器与判别器的平衡
3、生成器容易产生模式崩溃(Mode collapse)
- 举个生成数字图像的例子:生成器要生成0-9之间的数字,而判别器只是要判断生成器生成的数据像不像真实数据。
- 比如”1“是非常容易生成的一个数字,那么生成器可能就会拼命的去生成更多的真实的”1“,从而判别器就难以判别。对于其他的复杂一点的数字比如”8“,”9“,生成器可能就干脆不生成了,从而避免犯错,这就是生成器的一个大问题。
1.2 GAN在MNIST数据集上的应用
参考代码:PyTorch-GAN/implementations
1.2.1 生成器D和判别器G
- 我们这里实现的生成对抗网络(GAN)十分简单,仅用了线性层搭建。
- 生成器Generator将随机生成的噪声z通过多个线性层生成图片,
注意生成器的最后一层是Tanh,所以我们生成的图片的取值范围为[-1,1],同理,我们会将真实图片归一化(normalize)到[-1,1]。 - 判别器Discriminator是一个二分类器,通过多个线性层得到一个概率值来判别图片是"真实"或者是"生成"的,所以在Discriminator的最后是一个sigmoid,来得到图片是
真实的概率。 - 在所有的网络结构中我们都使用了LeakyReLU作为激活函数,除了G与D的最后一层。在层与层之间,我们还加入了BatchNormalization。
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import os
from PIL import Image
class Generator(nn.Module):
def __init__(self, image_size=32, latent_dim=100, output_channel=1):
"""
image_size: image with and height
latent dim: the dimension of random noise z
output_channel: the channel of generated image, for example, 1 for gray image, 3 for RGB image
"""
super(Generator, self).__init__()
self.latent_dim = latent_dim
self.output_channel = output_channel
self.image_size = image_size
# Linear layer: latent_dim -> 128 -> 256 -> 512 -> 1024 -> output_channel * image_size * image_size -> Tanh
self.model = nn.Sequential(
nn.Linear(latent_dim, 128),
nn.BatchNorm1d(128),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(128, 256),
nn.BatchNorm1d(256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 512),
nn.BatchNorm1d(512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(1024, output_channel * image_size * image_size),
nn.Tanh()
)
def forward(self, z):
img = self.model(z)
img = img.view(img.size(0), self.output_channel, self.image_size, self.image_size)
return img
class Discriminator(nn.Module):
def __init__(self, image_size=32, input_channel=1):
"""
image_size: image with and height
input_channel: the channel of input image, for example, 1 for gray image, 3 for RGB image
"""
super(Discriminator, self).__init__()
self.image_size = image_size
self.input_channel = input_channel
# Linear layer: input_channel * image_size * image_size -> 1024 -> 512 -> 256 -> 1 -> Sigmoid
self.model = nn.Sequential(
nn.Linear(input_channel * image_size * image_size, 1024),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(1024, 512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 1),
nn.Sigmoid(),
)
def forward(self, img):
img_flat = img.view(img.size(0), -1)
out = self.model(img_flat)
return out
1.2.2 MNIST数据集的加载
- MNIST是一个手写数字数据集,通常用于机器学习和计算机视觉领域的基准测试。每个样本都是一个28x28像素的灰度图像,表示从0到9的手写数字。
- MNIST数据集共包含70000个图像,其中60000个用作训练集,10000个用作测试集。对于GAN而言,我们不需要测试集,仅使用训练集。
- 我们将所有图片normalize到了[-1,1]之间。
def load_mnist_data():
"""
load mnist(0,1,2) dataset
"""
transform = torchvision.transforms.Compose([
# transform to 1-channel gray image since we reading image in RGB mode
transforms.Grayscale(1),
# resize image from 28 * 28 to 32 * 32
transforms.Resize(32),
transforms.ToTensor(),
# normalize with mean=0.5 std=0.5,
transforms.Normalize(mean=(0.5,),
std=(0.5,))
])
train_dataset = torchvision.datasets.MNIST(r"/root/autodl-fs/data/minist", download=False, train=True,
transform=transform)
return train_dataset
- 通过下面代码,我们能够查看数据集中的20张随机真实图片
def denorm(x):
# denormalize
out = (x + 1) / 2
return out.clamp(0, 1)
def show_train_dataset():
train_dataset = load_mnist_data()
trainloader = torch.utils.data.DataLoader(train_dataset, batch_size=20, shuffle=True)
grid = torchvision.utils.make_grid(denorm(next(iter(trainloader))[0]), nrow=5)
os.makedirs("gan_minist", exist_ok=True)
image_grid = Image.fromarray(grid.mul(255).permute(1, 2, 0).byte().numpy())
image_grid.save(f"./gan_minist/init.jpg")
1.2.3 模型的训练
- GAN的训练过程分为两步
- 第一步将随机噪声z喂给生成器G生成图片,然后将真实图片和生成器G生成的图片喂给判别器D,然后使用对应的loss函数反向传播优化判别器D。
- 第二步使用生成器G生成图片,并喂给判别器D,并使用对应的loss函数反向传播优化生成器G。
- 对于判别器D,最大化其优化目标可以通过最小化一个BCEloss来实现,其真实图片的标签设置为1,而生成图片的标签设置为0。
- 对于生成器G,也通过最小化一个BCEloss来实现,即将生成图片的标签设置为1即可。
- 当模型训练时,我们需要查看G生成的图片效果,下面的visualize_results代码便实现了这块内容。
需要注意的是,我们生成的图片都在[-1,1]。因此,我们需要将图片反向归一化(denorm)到[0,1]。
def visualize_results(epoch, G, device, z_dim, result_size=20):
epoch = str(epoch).zfill(3)
G.eval()
z = torch.rand(result_size, z_dim).to(device)
g_z = G(z)
grid = torchvision.utils.make_grid(denorm(g_z.detach().cpu()), nrow=5)
os.makedirs("gan_minist", exist_ok=True)
image_grid = Image.fromarray(grid.mul(255).permute(1, 2, 0).byte().numpy())
image_grid.save(f"./gan_minist/{epoch}.jpg")
def run_gan(trainloader, G, D, G_optimizer, D_optimizer, loss_func, n_epochs, device, latent_dim):
d_loss_hist = []
g_loss_hist = []
t_epochs = []
for epoch in range(n_epochs):
d_loss, g_loss = train_one_epoch(trainloader, G, D, G_optimizer, D_optimizer, loss_func, device,
z_dim=latent_dim)
print('Epoch {}: Train D loss: {:.4f}, G loss: {:.4f}'.format(epoch, d_loss, g_loss))
d_loss_hist.append(d_loss)
g_loss_hist.append(g_loss)
t_epochs.append(epoch)
if epoch == 0 or (epoch + 1) % 10 == 0:
# 每10个epoch 就可视化一下图像
visualize_results(epoch + 1, G, device, latent_dim)
return d_loss_hist, g_loss_hist, t_epochs
def train_one_epoch(trainloader, G, D, G_optimizer, D_optimizer, loss_func, device, z_dim):
"""
train a GAN with model G and D in one epoch
Args:
trainloader: data loader to train
G: model Generator
D: model Discriminator
G_optimizer: optimizer of G(etc. Adam, SGD)
D_optimizer: optimizer of D(etc. Adam, SGD)
loss_func: loss function to train G and D. For example, Binary Cross Entropy(BCE) loss function
device: cpu or cuda device
z_dim: the dimension of random noise z
"""
# set train mode
D.train()
G.train()
D_total_loss = 0
G_total_loss = 0
for i, (x, _) in enumerate(trainloader):
# real label and fake label
y_real = torch.ones(x.size(0), 1).to(device)
y_fake = torch.zeros(x.size(0), 1).to(device)
x = x.to(device)
z = torch.rand(x.size(0), z_dim).to(device)
# 1、训练判别器
# D optimizer zero grads
D_optimizer.zero_grad()
# D real loss from real images
d_real = D(x)
d_real_loss = loss_func(d_real, y_real)
# D fake loss from fake images generated by G
g_z = G(z)
d_fake = D(g_z)
d_fake_loss = loss_func(d_fake, y_fake)
# D backward and step
d_loss = d_real_loss + d_fake_loss
d_loss.backward()
D_optimizer.step()
# 2、训练生成器
# G optimizer zero grads
G_optimizer.zero_grad()
# G loss
g_z = G(z)
d_fake = D(g_z)
g_loss = loss_func(d_fake, y_real)
# G backward and step
g_loss.backward()
G_optimizer.step()
D_total_loss += d_loss.item()
G_total_loss += g_loss.item()
return D_total_loss / len(trainloader), G_total_loss / len(trainloader)
- 设置好超参数就可以开始训练,我们可以将训练过程中loss值记录下来方便画图
def save_loss2txt(x_values, y1_values, y2_values):
# 打开文件进行写入
with open('gan_minist/loss_data.txt', 'w') as file:
for x, y1, y2 in zip(x_values, y1_values, y2_values):
file.write(f'{x} {y1} {y2}\n')
def plot_loss():
# 然后使用matplotlib读取txt文件中的数据进行绘图
x_values, y1_values, y2_values = [], [], []
with open('gan_minist/loss_data.txt', 'r') as file:
for line in file:
parts = line.split()
x_values.append(float(parts[0]))
y1_values.append(float(parts[1]))
y2_values.append(float(parts[2]))
# 绘图
plt.plot(x_values, y1_values, label='d_loss_hist')
plt.plot(x_values, y2_values, label='g_loss_hist')
plt.legend()
plt.show()
if __name__ == '__main__':
# hyper params
# z dim
latent_dim = 100
# image size and channel
image_size = 32
image_channel = 1
# Adam lr and betas
learning_rate = 0.0002
betas = (0.5, 0.999)
# epochs and batch size
n_epochs = 200
batch_size = 512
# device
device = "cuda" if torch.cuda.is_available() else "cpu"
# mnist dataset and dataloader
train_dataset = load_mnist_data()
trainloader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True, num_workers=12)
# use BCELoss as loss function
bceloss = nn.BCELoss().to(device)
# G and D model
G = Generator(image_size=image_size, latent_dim=latent_dim, output_channel=image_channel).to(device)
D = Discriminator(image_size=image_size, input_channel=image_channel).to(device)
# G and D optimizer, use Adam or SGD
G_optimizer = optim.Adam(G.parameters(), lr=learning_rate, betas=betas)
D_optimizer = optim.Adam(D.parameters(), lr=learning_rate, betas=betas)
d_loss_hist, g_loss_hist, t_epochs = run_gan(trainloader, G, D, G_optimizer, D_optimizer, bceloss,
n_epochs, device, latent_dim)
# 保存Loss信息
save_loss2txt(t_epochs, d_loss_hist, g_loss_hist)
- 下面是训练第1、100、200轮时,随机生成的图像。
- 可以看到,即使是一个简单的GAN在MNIST这种简单数据集上的生成效果还是不错的。

- 训练过程中的损失函数图像如下所示。
- 我们知道在训练过程中,一般损失曲线倾向于下降并最终收敛。然而,在生成对抗网络(GAN)模型中,当判别器(D_loss)降低时,生成器损失(G_loss)升高,反之亦然。
- 这是因为在GAN中,生成器和判别器相互对抗,生成器希望生成的图像能够欺骗判别器,而判别器希望能够找到生成器的伪装,因此两者的表现往往是相反的。

2 CGAN的简述及其在MNIST数据集上的应用
2.1 CGAN的简述
- 原始GAN的生成过程采用随机噪声就可以开始训练,不再需要一个假设的数据分布,但是这样自由散漫的方式对于较大的图像就不太可控了
- CGAN(Conditional GAN)方法提出了一种带有条件约束的GAN,通过额外的信息对模型增加条件,来指导数据生成过程。
- 将额外信息y输送给判别模型和生成模型,作为输入层的一部分,从而实现条件GAN,是在Mnist数据集上以类别标签为条件变量,生成指定类别的图像,把纯无监督的GAN变成有监督的模型。

- 条件 GAN 的目标函数是带有条件概率的二人极小极大值博弈

- 论文链接:https://arxiv.org/pdf/1411.1784.pdf
2.2 CGAN在MNIST数据集上的应用
- 我们在GAN的基础上,利用nn.Embedding(10, label_latent_dim)将labels进行映射
- 再利用torch.cat([z, label_embedding], dim=-1)拼接起来就得到了CGAN。
import torch
from tqdm import trange
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import os
from PIL import Image
class Generator(nn.Module):
def __init__(self, image_size=32, latent_dim=100, output_channel=1, label_latent_dim=10):
"""
image_size: image with and height
latent dim: the dimension of random noise z
output_channel: the channel of generated image, for example, 1 for gray image, 3 for RGB image
"""
super(Generator, self).__init__()
self.latent_dim = latent_dim
self.output_channel = output_channel
self.image_size = image_size
self.embedding = nn.Embedding(10, label_latent_dim)
# Linear layer: latent_dim -> 128 -> 256 -> 512 -> 1024 -> output_channel * image_size * image_size -> Tanh
self.model = nn.Sequential(
nn.Linear(latent_dim + label_latent_dim, 128),
nn.BatchNorm1d(128),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(128, 256),
nn.BatchNorm1d(256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 512),
nn.BatchNorm1d(512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 1024),
nn.BatchNorm1d(1024),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(1024, output_channel * image_size * image_size),
nn.Tanh()
)
def forward(self, z, labels):
# concat 标签向量
label_embedding = self.embedding(labels)
z = torch.cat([z, label_embedding], dim=-1)
img = self.model(z)
img = img.view(img.size(0), self.output_channel, self.image_size, self.image_size)
return img
class Discriminator(nn.Module):
def __init__(self, image_size=32, input_channel=1, label_latent_dim=10):
"""
image_size: image with and height
input_channel: the channel of input image, for example, 1 for gray image, 3 for RGB image
"""
super(Discriminator, self).__init__()
self.image_size = image_size
self.input_channel = input_channel
self.embedding = nn.Embedding(10, label_latent_dim)
# Linear layer: input_channel * image_size * image_size -> 1024 -> 512 -> 256 -> 1 -> Sigmoid
self.model = nn.Sequential(
nn.Linear(input_channel * image_size * image_size + label_latent_dim, 1024),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(1024, 512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 1),
nn.Sigmoid(),
)
def forward(self, img, labels):
img_flat = img.view(img.size(0), -1)
# concat 标签向量
label_embedding = self.embedding(labels)
img_flat = torch.cat([img_flat, label_embedding], dim=-1)
out = self.model(img_flat)
return out
- 注意此时的训练函数中,需要传入lables信息了。
- 其他函数,和GAN一致。
def train_one_epoch(trainloader, G, D, G_optimizer, D_optimizer, loss_func, device, z_dim):
"""
train a CGAN with model G and D in one epoch
Args:
trainloader: data loader to train
G: model Generator
D: model Discriminator
G_optimizer: optimizer of G(etc. Adam, SGD)
D_optimizer: optimizer of D(etc. Adam, SGD)
loss_func: loss function to train G and D. For example, Binary Cross Entropy(BCE) loss function
device: cpu or cuda device
z_dim: the dimension of random noise z
"""
# set train mode
D.train()
G.train()
D_total_loss = 0
G_total_loss = 0
for i, (x, labels) in enumerate(trainloader):
# real label and fake label
y_real = torch.ones(x.size(0), 1).to(device)
y_fake = torch.zeros(x.size(0), 1).to(device)
x = x.to(device)
labels = labels.to(device)
z = torch.rand(x.size(0), z_dim).to(device)
# 1、训练判别器
# D optimizer zero grads
D_optimizer.zero_grad()
# D real loss from real images
d_real = D(x, labels)
d_real_loss = loss_func(d_real, y_real)
# D fake loss from fake images generated by G
g_z = G(z, labels)
d_fake = D(g_z, labels)
d_fake_loss = loss_func(d_fake, y_fake)
# D backward and step
d_loss = d_real_loss + d_fake_loss
d_loss.backward()
D_optimizer.step()
# 2、训练生成器
# G optimizer zero grads
G_optimizer.zero_grad()
# G loss
g_z = G(z, labels)
d_fake = D(g_z, labels)
g_loss = loss_func(d_fake, y_real)
# G backward and step
g_loss.backward()
G_optimizer.step()
D_total_loss += d_loss.item()
G_total_loss += g_loss.item()
return D_total_loss / len(trainloader), G_total_loss / len(trainloader)
- 下面是训练第1、100、200轮时,随机生成的图像。

3 DCGAN的简述及其在MNIST数据集上的应用
3.1 DCGAN的简述
-
DCGAN使用卷积层代替了全连接层,采用带步长的卷积代替上采样,更好的提取图像特征,判别器和生成器对称存在,极大的提升了GAN训练的稳定性和生成结果的质量。
-
判别器中采用leakyRELU而不是RELU来防止梯度稀疏,而生成器仍然采用RELU,但输出层采用tanh。采用Adam优化器训练GAN,设置学习率为0.0002。
-
DCGAN并没有从根本上解决GAN训练不稳定的问题,训练的时候仍需要小心的平衡生成器和判别器的训练,往往是训练一个多次,训练另一个一次。
-
论文链接:https://arxiv.org/pdf/1511.06434.pdf
3.2 DCGAN在MNIST数据集上的应用
-
在DCGAN(Deep Convolution GAN)中,最大的改变是使用了CNN代替全连接层。
- 在生成器G中,使用stride为2的转置卷积来生成图片同时扩大图片尺寸;
- 而在判别器D中,使用stride为2的卷积来将图片进行卷积并下采样。
-
除此之外,DCGAN加入了在层与层之间BatchNormalization(虽然我们在普通的GAN中就已经添加),在G中使用ReLU作为激活函数,而在D中使用LeakyReLU作为激活函数
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import os
from PIL import Image
class DCGenerator(nn.Module):
def __init__(self, image_size=32, latent_dim=64, output_channel=1):
super(DCGenerator, self).__init__()
self.image_size = image_size
self.latent_dim = latent_dim
self.output_channel = output_channel
self.init_size = image_size // 8
# fc: Linear -> BN -> ReLU
self.fc = nn.Sequential(
nn.Linear(latent_dim, 512 * self.init_size ** 2),
nn.BatchNorm1d(512 * self.init_size ** 2),
nn.ReLU(inplace=True)
)
# deconv: ConvTranspose2d(4, 2, 1) -> BN -> ReLU ->
# ConvTranspose2d(4, 2, 1) -> BN -> ReLU ->
# ConvTranspose2d(4, 2, 1) -> Tanh
self.deconv = nn.Sequential(
nn.ConvTranspose2d(512, 256, 4, stride=2, padding=1),
nn.BatchNorm2d(256),
nn.ReLU(inplace=True),
nn.ConvTranspose2d(256, 128, 4, stride=2, padding=1),
nn.BatchNorm2d(128),
nn.ReLU(inplace=True),
nn.ConvTranspose2d(128, output_channel, 4, stride=2, padding=1),
nn.Tanh(),
)
def forward(self, z):
out = self.fc(z)
out = out.view(out.shape[0], 512, self.init_size, self.init_size)
img = self.deconv(out)
return img
class DCDiscriminator(nn.Module):
def __init__(self, image_size=32, input_channel=1, sigmoid=True):
super(DCDiscriminator, self).__init__()
self.image_size = image_size
self.input_channel = input_channel
self.fc_size = image_size // 8
# conv: Conv2d(3,2,1) -> LeakyReLU
# Conv2d(3,2,1) -> BN -> LeakyReLU
# Conv2d(3,2,1) -> BN -> LeakyReLU
self.conv = nn.Sequential(
nn.Conv2d(input_channel, 128, 3, 2, 1),
nn.LeakyReLU(0.2),
nn.Conv2d(128, 256, 3, 2, 1),
nn.BatchNorm2d(256),
nn.LeakyReLU(0.2),
nn.Conv2d(256, 512, 3, 2, 1),
nn.BatchNorm2d(512),
nn.LeakyReLU(0.2),
)
# fc: Linear -> Sigmoid
self.fc = nn.Sequential(
nn.Linear(512 * self.fc_size * self.fc_size, 1),
)
if sigmoid:
self.fc.add_module('sigmoid', nn.Sigmoid())
def forward(self, img):
out = self.conv(img)
out = out.view(out.shape[0], -1)
out = self.fc(out)
return out
- 同样使用mnist数据集对DCGAN进行训练,训练代码只需要修改G、D模型分别为DCGenerator、DCDiscriminator。
- 其他代码和GAN一致。
if __name__ == '__main__':
# hyper params
# z dim
latent_dim = 100
# image size and channel
image_size = 32
image_channel = 1
# Adam lr and betas
learning_rate = 0.0002
betas = (0.5, 0.999)
# epochs and batch size
n_epochs = 200
batch_size = 512
# device
device = "cuda" if torch.cuda.is_available() else "cpu"
# mnist dataset and dataloader
train_dataset = load_mnist_data()
trainloader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True, num_workers=12)
# use BCELoss as loss function
bceloss = nn.BCELoss().to(device)
# G and D model
G = DCGenerator(image_size=image_size, latent_dim=latent_dim, output_channel=image_channel).to(device)
D = DCDiscriminator(image_size=image_size, input_channel=image_channel).to(device)
# G and D optimizer, use Adam or SGD
G_optimizer = optim.Adam(G.parameters(), lr=learning_rate, betas=betas)
D_optimizer = optim.Adam(D.parameters(), lr=learning_rate, betas=betas)
d_loss_hist, g_loss_hist, t_epochs = run_gan(trainloader, G, D, G_optimizer, D_optimizer, bceloss,
n_epochs, device, latent_dim)
# 保存Loss信息
save_loss2txt(t_epochs, d_loss_hist, g_loss_hist)
- 下面是训练第1、100、200轮时,随机生成的图像。

4 LSGAN的简述及其在MNIST数据集上的应用
4.1 LSGAN的简述
- LSGAN(最小二乘GAN)采用最小二乘损失函数代替原始GAN的交叉熵损失函数
- 主要针对原始GAN生成器生成的图像质量不高和训练过程不稳定两个问题
- 作者认为以交叉熵作为损失,会使得生成器不会再优化那些被判别器识别为真实图片的生成图片,即使这些生成图片距离判别器的决策边界仍然很远,也就是距真实数据比较远。这意味着生成器的生成图片质量并不高。
- 为什么生成器不再优化优化生成图片呢?这是因为生成器已经完成我们为它设定的目标——尽可能地混淆判别器,所以交叉熵损失已经很小了。
- 而最小二乘就不一样了,要想最小二乘损失比较小,在混淆判别器的前提下还得让生成器把距离决策边界比较远的生成图片拉向决策边界。
- 损失函数定义如下:

-
sigmoid交叉熵损失很容易就达到饱和状态(饱和是指梯度为0),而最小二乘损失只在一点达到饱和,因此LSGAN使得GAN的训练更加稳定。

-
论文链接:https://arxiv.org/pdf/1611.04076.pdf
4.2 LSGAN在MNIST数据集上的应用
- 我们在CGAN基础上,修改为LSGAN,只修改一行代码即可。
# bceloss = nn.BCELoss().to(device)
mseloss = nn.MSELoss().to(device)
下面是训练第1、100、200轮时,随机生成的图像。

训练过程中的损失函数如下: