[数据结构1.0]快速排序

news2024/11/20 1:49:45

最近学习了快速排序，鼠鼠俺来做笔记了！

本篇博客用排升序为例介绍快速排序！

1.快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

如果对上面的介绍蒙圈的话，没关系，我们继续看下面的内容，会仔细介绍的！

1.1.快速排序的”单趟“

快速排序的”单趟“简单来说就是在需排序乱序数组中任取一个元素作为基准值，经过”单趟“过后，大于或者等于基准值的元素都排在基准值的后面，小于或者等于基准值的元素都排在基准值的前面，也就是说基准值所在的位置就是它应该出现的位置，这个基准值就排好了！

对于”单趟“的实现方法有但不限于下面三种：

1.1.1.hoare版本

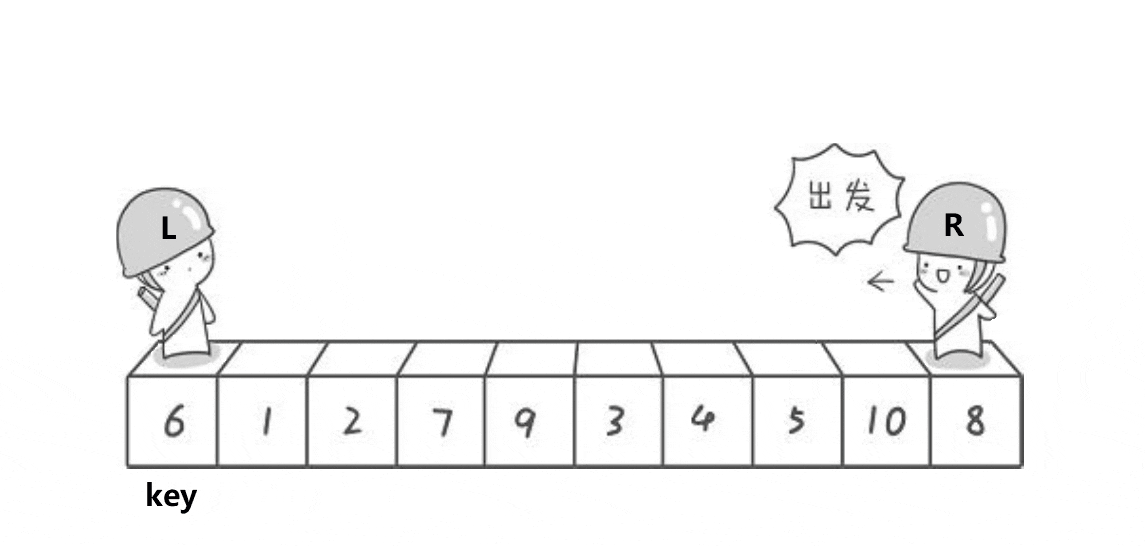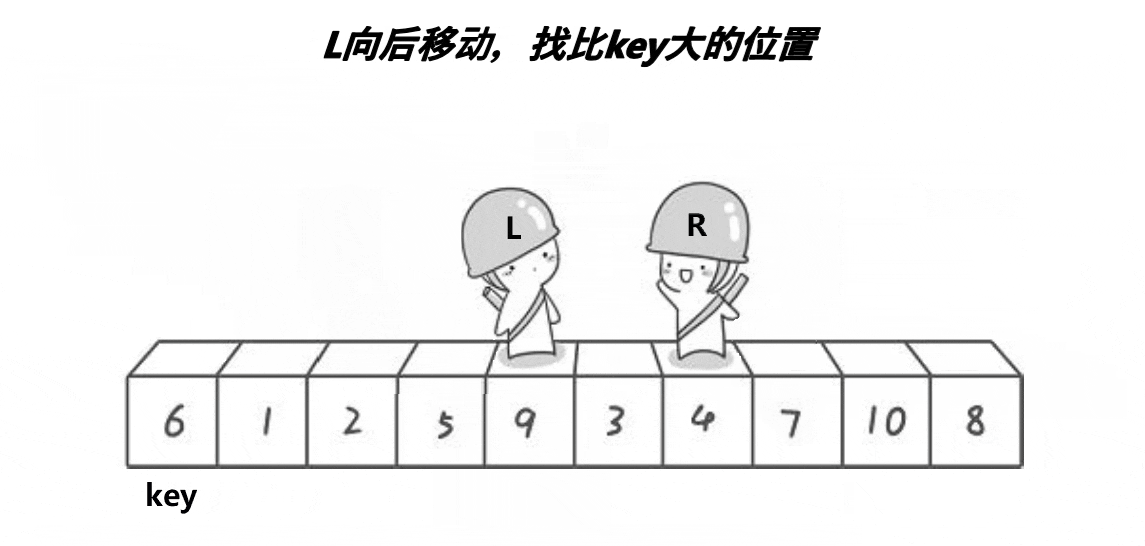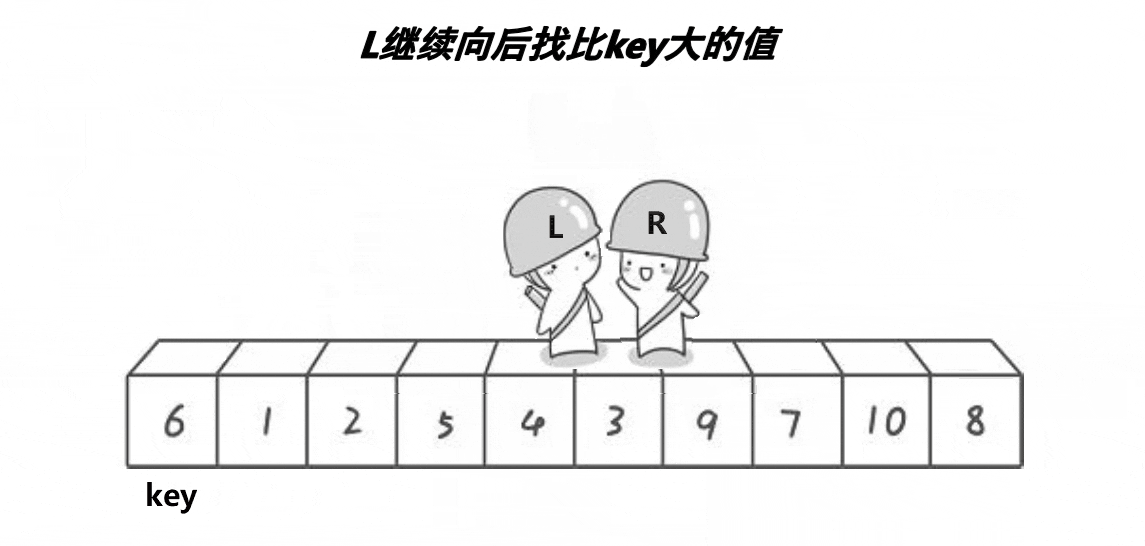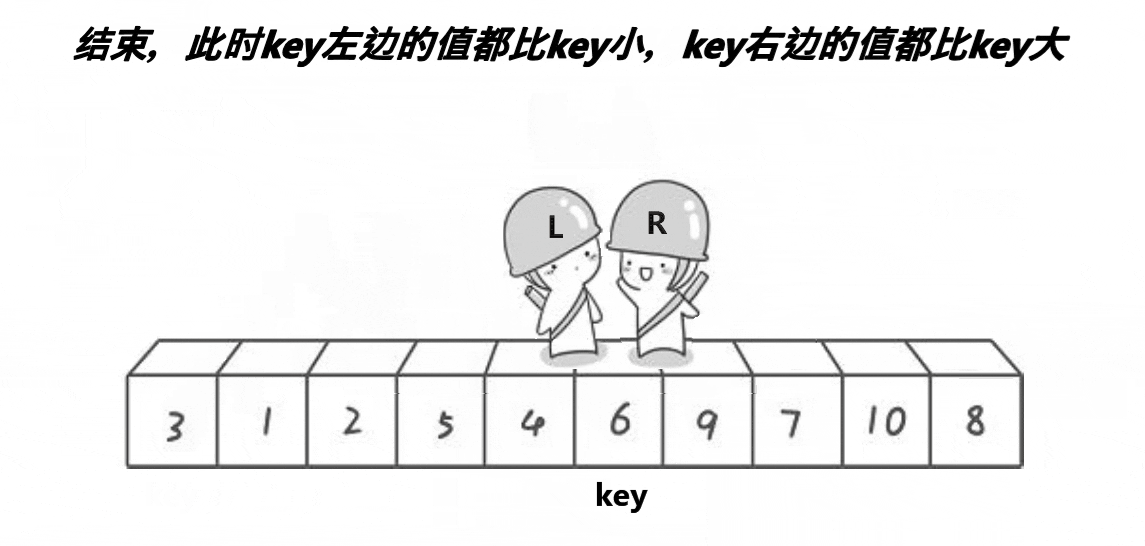
这个动图就是hoare版本的”单趟“实现方法！这里取第一个元素6为基准值；R从最”右边“开始找比基准值小的元素，L从最”左边“开始找比基准值大的元素， 然后交换下标为R和L的元素；R继续找比基准值小的元素，L继续找比基准值大的元素，再交换下标为R和L的元素…………直到R和L相遇，将基准值和相遇位置的元素即可！

其实这个本质就是将比基准值大的元素”甩“到”后面“，将比基准值小的元素”甩“到”前面“。

也许会有疑问，怎么保证相遇位置的元素一定不大于基准值呢？

因为只要是R先动，L后动的话必然能保证相遇的元素一定不大于基准值！

相遇无非两种情况：

1.R遇L：R在去找小于基准值的元素的过程中，下标为L的元素必然是不大于基准值的元素。当R去找小于基准值的元素没有找到却遇到L时， 那么相遇位置的值就是不大于基准值的元素。

2.L遇R：由于R先动，那么L在找大于基准值的元素的过程中，下标为R的元素必然是不大于基准值的元素。当L去找大于基准值的元素没有找到却遇到R时，那么相遇位置的值就是不大于基准值的元素。

 hoare版本的“单趟”代码如下，需排序乱序数组下标为begin—end：

//hoare版本
	int keyi = begin;
	int left = begin, right = end;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[right]);
	keyi = right;

由于hoare版本写起来很容易出错误，所以我们一般写下面两种版本！

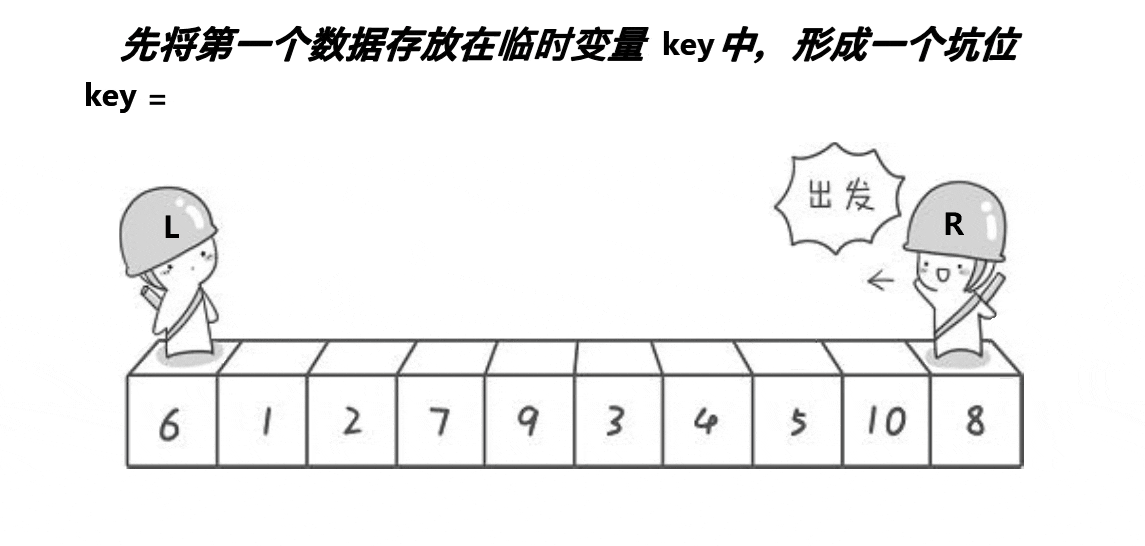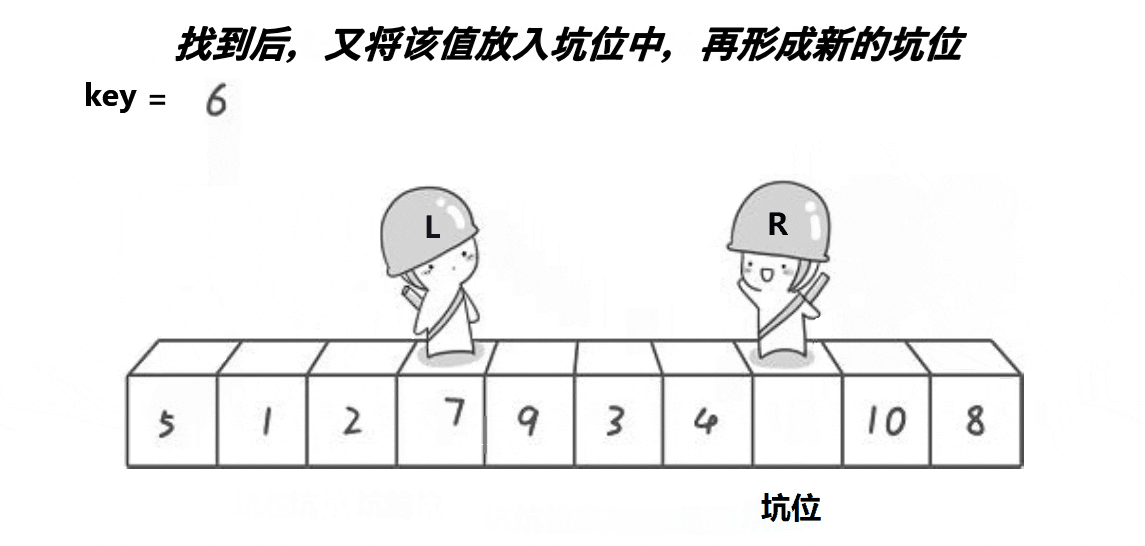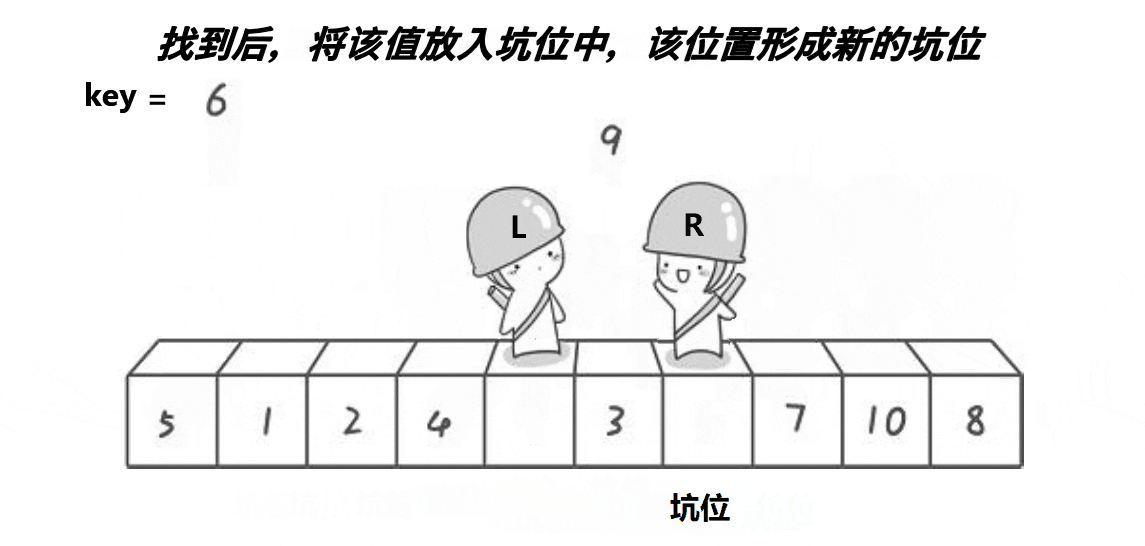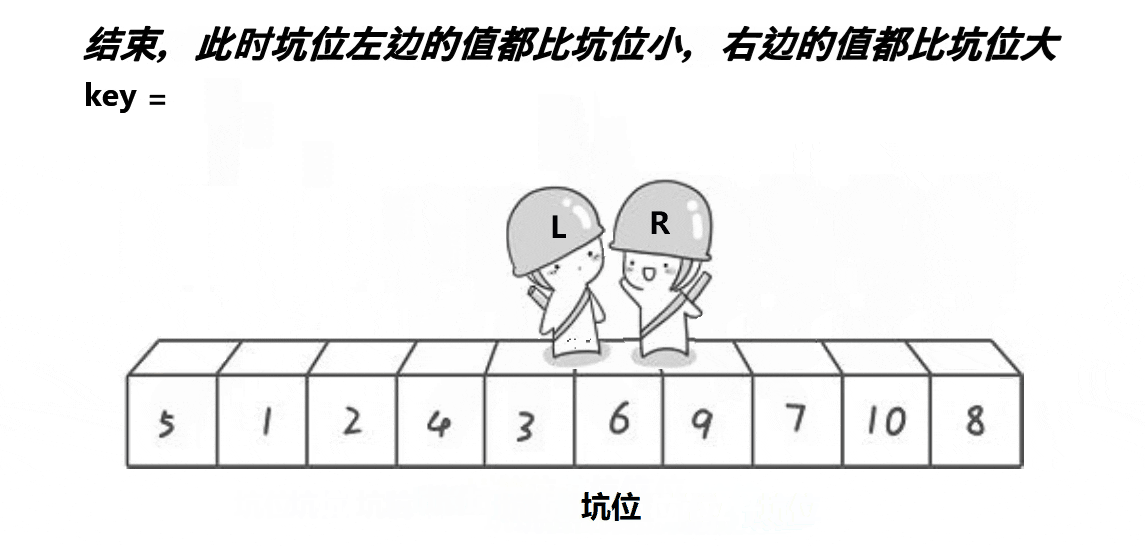
1.1.2.挖坑法版本

也是取第一个元素6为基准值。初始坑位设置为基准值下标。让R从最“右边”开始找比基准值小的元素，找到后将下标为R的元素填入坑位，那么新的坑位就变成了R；让L从最“左边”开始找比基准值大的元素，找到后将下标为L的元素填入坑位，那么新的坑位就变成了L；R再找比基准值小的元素……直到R和L相遇，将基准值填入坑位即可。

本质就是R找小填入“左边”坑位，L找大填入“右边”坑位，最后一个坑位必定是R和L相遇位置，填入基准值就好。

挖坑法版本“单趟”代码如下，需排序乱序数组下标为begin—end：

//挖坑法版本
	int  key=a[begin];
	int left = begin, right = end;
	int hole = begin;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
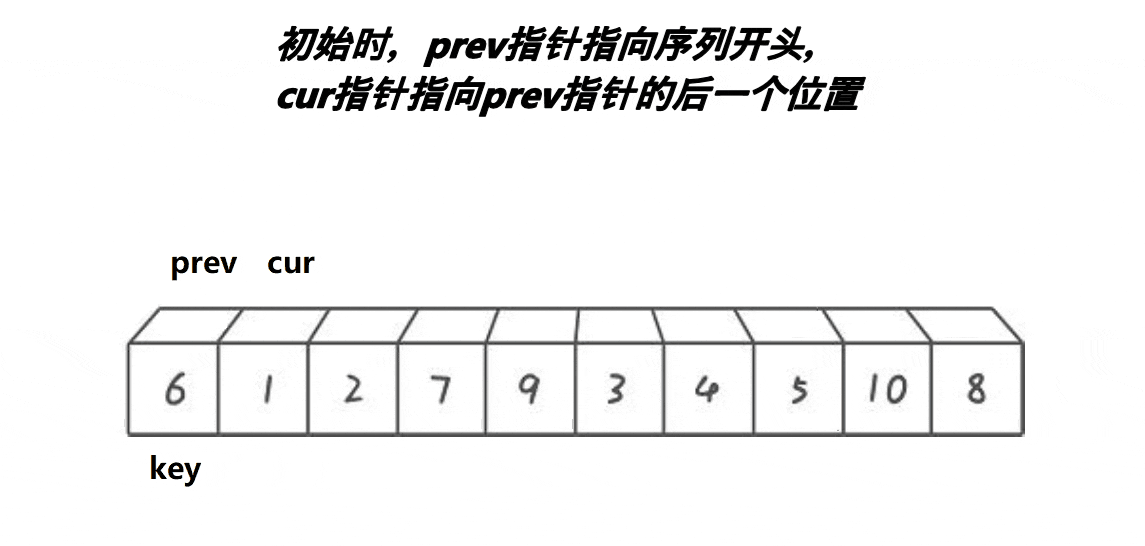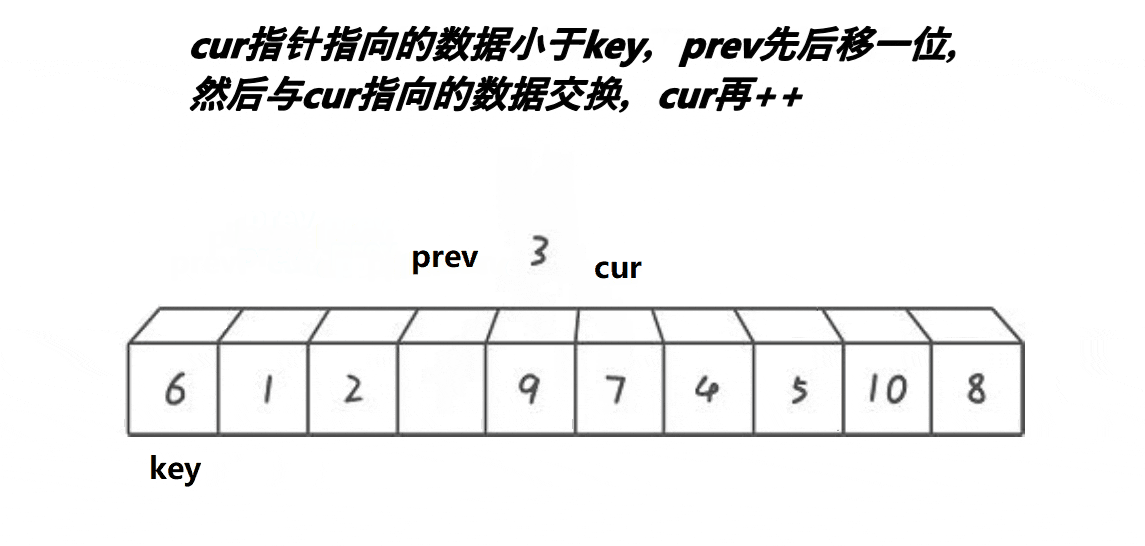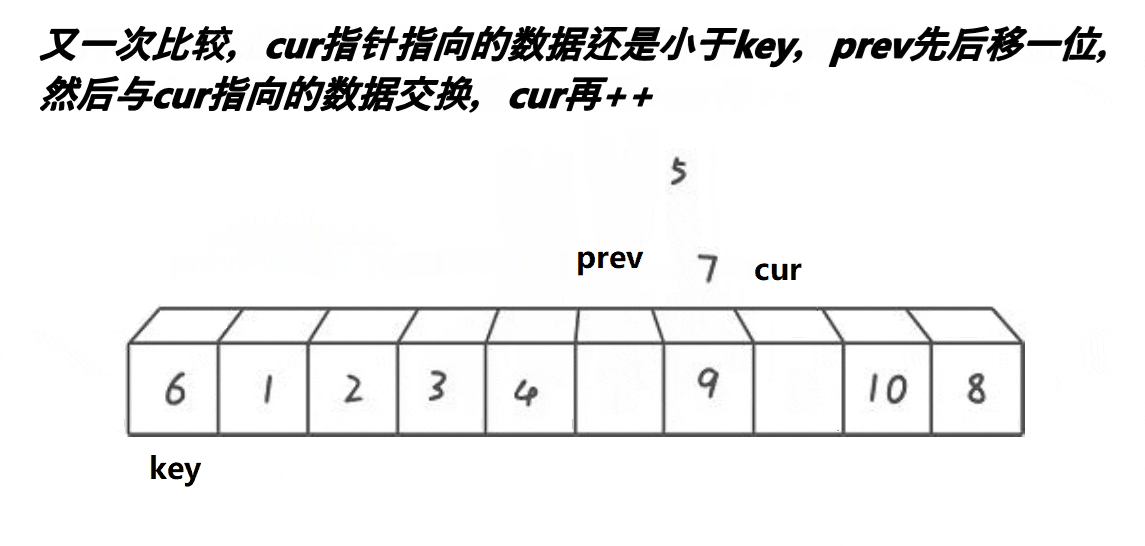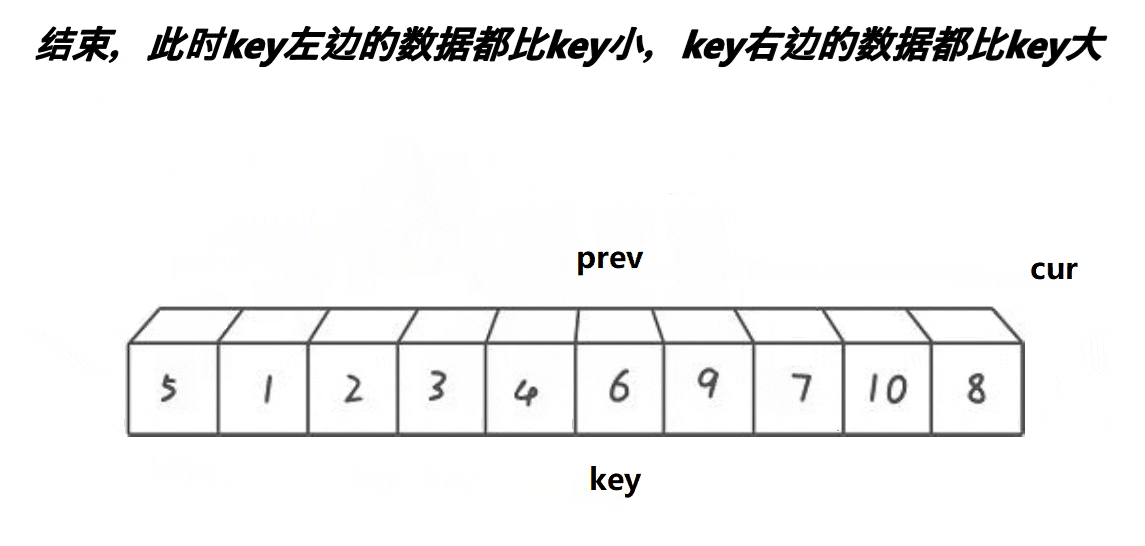
	int keyi = hole;
1.1.3.前后指针版本

取第一个元素6为基准值。prev初始指向基准值，cur初始指向基准值的下一个元素。cur遍历数组：如果cur遇到大于基准值的元素，++cur；否则++prev、cur指向的元素和prev指向的元素交换、++cur。

前后指针版本“单趟”代码如下， 需排序乱序数组下标为begin—end：

//前后指针版本
	int cur = begin + 1, prev = begin;
	int keyi = begin;
	while (cur <= end)
	{
		if (a[cur] > a[keyi])
		{
			++cur;
		}
		else
		{
			++prev;
			Swap(&a[prev], &a[cur]);
			++cur;
		}
	}
	Swap(&a[keyi], &a[prev]);
	keyi = prev;

这里指针写成了下标的形式，思想没变，本质上还是一样的！

1.2.快速排序的递归写法 

经过“单趟”过后，被选中的基准值就排在了它该出现的位置，就是说当数组排好变得有序后，基准值就在“单趟”过后出现的位置！

既然基准值已经拍好了，如果基准值的“左边”的元素集合能有序并且基准值的“右边”的元素集合能有序，那么需排序的乱序数组就排好了，变得有序了。举个例子：

如图， 所以说快速排序一种二叉树结构的交换排序方法。进行“单趟”排好基准值，递归“左边”元素集合…………“左边”元素集合排好后，递归“右边”元素集合…………“右边”元素集合排好后就搞定了！

递归结束条件：当元素集合只有1个值或为空。

看看快速排序的递归写法代码：

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	
	//hoare版本
	/*int keyi = begin;
	int left = begin, right = end;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[right]);
	keyi = right;*/

	//挖坑法版本
	int  key=a[begin];
	int left = begin, right = end;
	int hole = begin;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	int keyi = hole;

	//前后指针版本
	/*int cur = begin + 1, prev = begin;
	int keyi = begin;
	while (cur <= end)
	{
		if (a[cur] > a[keyi])
		{
			++cur;
		}
		else
		{
			++prev;
			Swap(&a[prev], &a[cur]);
			++cur;
		}
	}
	Swap(&a[keyi], &a[prev]);
	keyi = prev;*/

	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

我们试试这个快速排序：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>

void PrintArrar(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	
	//hoare版本
	/*int keyi = begin;
	int left = begin, right = end;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[right]);
	keyi = right;*/

	//挖坑法版本
	/*int  key=a[begin];
	int left = begin, right = end;
	int hole = begin;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			right--;;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	int keyi = hole;*/

	//前后指针版本
	int cur = begin + 1, prev = begin;
	int keyi = begin;
	while (cur <= end)
	{
		if (a[cur] > a[keyi])
		{
			++cur;
		}
		else
		{
			++prev;
			Swap(&a[prev], &a[cur]);
			++cur;
		}
	}
	Swap(&a[keyi], &a[prev]);
	keyi = prev;

	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

int main()
{
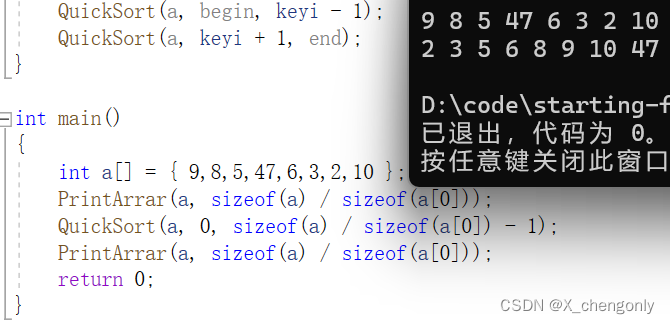
	int a[] = { 9,8,5,47,6,3,2,10 };
	PrintArrar(a, sizeof(a) / sizeof(a[0]));
	QuickSort(a, 0, sizeof(a) / sizeof(a[0]) - 1);
	PrintArrar(a, sizeof(a) / sizeof(a[0]));
	return 0;
}

没问题的：

1.3.快速排序的非递归写法

鼠鼠这里介绍一种快速排序的非递归写法。

需要用到鼠鼠前面博客 介绍的栈，利用到栈写的快速排序没有用到递归但思想却很像递归！

 非递归写法思想如上图。我们看快速排序非递归代码如下，其中变量s是栈。鼠鼠这里“单趟”选择挖坑法版本，当然老爷们可以用其他版本：

void QuickSortNonr(int* a, int begin, int end)
{
	Stack s;
	StackInit(&s);
	StackPush(&s, end);
	StackPush(&s, begin);
	while (!StackEmpty(&s))
	{
		int start = StackTop(&s);
		StackPop(&s);
		int finish = StackTop(&s);
		StackPop(&s);

		int  key = a[start];
		int left = start, right = finish;
		int hole = start;
		while (left < right)
		{
			while (left < right && a[right] >= key)
			{
				right--;;
			}
			a[hole] = a[right];
			hole = right;
			while (left < right && a[left] <= key)
			{
				left++;
			}
			a[hole] = a[left];
			hole = left;
		}
		a[hole] = key;

		if (start < left - 1)
		{
			StackPush(&s, left - 1);
			StackPush(&s, start);
		}
		if (left + 1 < finish)
		{
			StackPush(&s, finish);
			StackPush(&s, left + 1);
		}
	}
	StackDestroy(&s);
}

我们要用到栈，所以记得将我们自己写的栈的头文件和源文件拷贝一份到快速排序的工程目录下 ，再包栈的头文件就可以用了。我们试试：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include"Stack.h" //注意包含栈的头文件

void PrintArrar(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

void QuickSortNonr(int* a, int begin, int end)
{
	Stack s;
	StackInit(&s);
	StackPush(&s, end);
	StackPush(&s, begin);
	while (!StackEmpty(&s))
	{
		int start = StackTop(&s);
		StackPop(&s);
		int finish = StackTop(&s);
		StackPop(&s);

		int  key = a[start];
		int left = start, right = finish;
		int hole = start;
		while (left < right)
		{
			while (left < right && a[right] >= key)
			{
				right--;;
			}
			a[hole] = a[right];
			hole = right;
			while (left < right && a[left] <= key)
			{
				left++;
			}
			a[hole] = a[left];
			hole = left;
		}
		a[hole] = key;

		if (start < left - 1)
		{
			StackPush(&s, left - 1);
			StackPush(&s, start);
		}
		if (left + 1 < finish)
		{
			StackPush(&s, finish);
			StackPush(&s, left + 1);
		}
	}
	StackDestroy(&s);
}

int main()
{
	int a[] = { 9,8,5,47,6,3,2,10 };
	PrintArrar(a, sizeof(a) / sizeof(a[0]));
	QuickSortNonr(a, 0, sizeof(a) / sizeof(a[0]) - 1);
	PrintArrar(a, sizeof(a) / sizeof(a[0]));
	return 0;
}

 没问题吧！

2.快速排序递归写法优化 

2.1.三数取中法选基准值

对于递归写法来说，对于需排序数组本身就是升序或者降序的情况适应的不是很好，因为：

1.固定了选择元素集合第一个元素为基准值，每次“单趟”过后都会导致某一边元素集合为空的情况。这样的话如果本身就是升序或者降序的需排序数组个数有n个的话，就要递归n层，很容易栈溢出！

2.每次“单趟”时间复杂度是O(N)，递归n层的话快速排序时间复杂度是O(N^2)，时间效率不划算！

所以我们有三数取中选基准值，我们取元素集合第一个元素、最后一个元素和中间那个元素，这三个元素比较得出第二大的元素，将这个元素与元素集合第一个元素交换再进行“单趟”。

这样的话就能很好适应需排序数组本身就是升序或者降序的情况，因为这样经过“单趟”之后，基准值一定会出现在“中间”。这样子去递归的话，每一层递归都会被“二分”，递归层数大大减少，递归log(N)层就行！

加入了三数取中选基准值的递归写法的快速排序时间复杂度是O(N*logN)。

而且加入了三数取中选基准值的递归写法的快速排序对于需排序数组本身不是升序或者降序的情况一样有帮助，可以让每层递归尽量“二分”，从而减少递归层数！

三数取中法代码：

int GetMidi(int* a, int begin, int end)
{
	int midi = begin + (end - begin) / 2;
	if (a[begin] > a[midi])
	{
		if (a[begin] > a[end])
		{
			if (a[midi] > a[end])
			{
				return midi;
			}
			else
				return end;
		}
		else
		{
			return begin;
		}
	}
	else
	{
		if (a[midi] > a[end])
		{
			if (a[end] > a[begin])
			{
				return end;
			}
			else
			{
				return begin;
			}
		}
		else
		{
			return midi;
		}
	}
}

当没有加入三数取中选基准值的递归写法的快速排序排10000个升序元素组成的数组时，在Debug环境下就会崩溃，栈溢出了：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<time.h>

int GetMidi(int* a, int begin, int end)
{
	int midi = begin + (end - begin) / 2;
	if (a[begin] > a[midi])
	{
		if (a[begin] > a[end])
		{
			if (a[midi] > a[end])
			{
				return midi;
			}
			else
				return end;
		}
		else
		{
			return begin;
		}
	}
	else
	{
		if (a[midi] > a[end])
		{
			if (a[end] > a[begin])
			{
				return end;
			}
			else
			{
				return begin;
			}
		}
		else
		{
			return midi;
		}
	}
}

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	//三数取中选基准值
	/*int midi = GetMidi(a, begin, end);
	Swap(&a[begin], &a[midi]);*/

	//前后指针版本
	int cur = begin + 1, prev = begin;
	int keyi = begin;
	while (cur <= end)
	{
		if (a[cur] > a[keyi])
		{
			++cur;
		}
		else
		{
			++prev;
			Swap(&a[prev], &a[cur]);
			++cur;
		}
	}
	Swap(&a[keyi], &a[prev]);
	keyi = prev;

	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

int main()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand((unsigned int)time(0));
	a[0] = rand();
	for (int i = 1; i < n ; i++)
	{
		a[i] = a[i-1] + 1;
	}
	int begin = clock();
	QuickSort(a, 0, n - 1);
	int end = clock();
	printf("%d\n", end - begin);
	return 0;
}

结果：

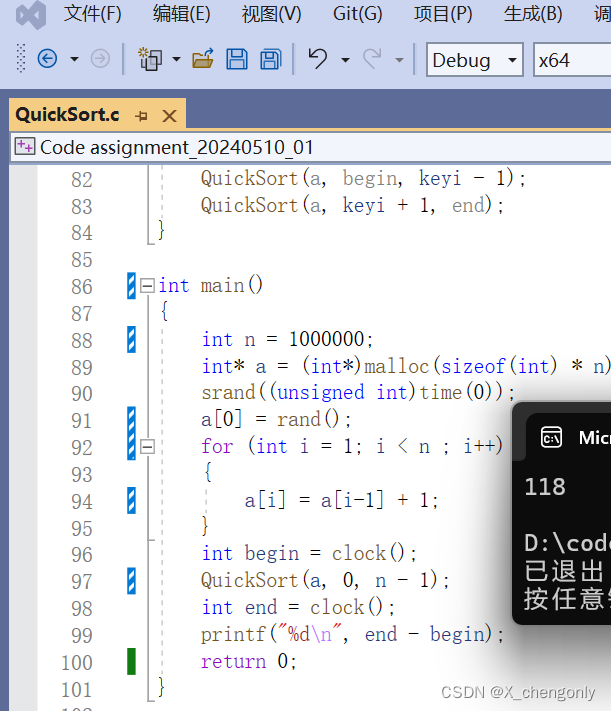
当加入三数取中选基准值的递归写法的快速排序，排100w个升序元素组成的数组都没问题，Debug环境下：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<time.h>

int GetMidi(int* a, int begin, int end)
{
	int midi = begin + (end - begin) / 2;
	if (a[begin] > a[midi])
	{
		if (a[begin] > a[end])
		{
			if (a[midi] > a[end])
			{
				return midi;
			}
			else
				return end;
		}
		else
		{
			return begin;
		}
	}
	else
	{
		if (a[midi] > a[end])
		{
			if (a[end] > a[begin])
			{
				return end;
			}
			else
			{
				return begin;
			}
		}
		else
		{
			return midi;
		}
	}
}

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	//三数取中选基准值
	int midi = GetMidi(a, begin, end);
	Swap(&a[begin], &a[midi]);

	//前后指针版本
	int cur = begin + 1, prev = begin;
	int keyi = begin;
	while (cur <= end)
	{
		if (a[cur] > a[keyi])
		{
			++cur;
		}
		else
		{
			++prev;
			Swap(&a[prev], &a[cur]);
			++cur;
		}
	}
	Swap(&a[keyi], &a[prev]);
	keyi = prev;

	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

int main()
{
	int n = 1000000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand((unsigned int)time(0));
	a[0] = rand();
	for (int i = 1; i < n ; i++)
	{
		a[i] = a[i-1] + 1;
	}
	int begin = clock();
	QuickSort(a, 0, n - 1);
	int end = clock();
	printf("%d\n", end - begin);
	return 0;
}

 结果：

2.2.小区间优化

递归到小的子区间（数量少的元素集合）时，可以考虑使用插入排序。这样子可以减少大部分的递归，因为大部分的递归都是由小的子区间产生的。不过由于编译器优化的厉害，小区间优化效果不是很明显，鼠鼠就在这里顺便提一提算了！

感谢阅读！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1675314.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

公示！教育部最新文件，9所新大学来了！

公示！教育部最新文件，9所新大学来了！

【SciencePub学术】5 月 13 日&#xff0c;教育部发布《关于拟同意设置本科高等学校的公示》。 根据《中华人民共和国高等教育法》《普通高等学校设置暂行条例》《普通本科学校设置暂行规定》《本科层次职业学校设置标准&#xff08;试行&#xff09;》等有关规定以及第八届全国…
阅读更多...
手撸XXL-JOB（三）——本地定时任务管理平台

手撸XXL-JOB（三）——本地定时任务管理平台

引言 在XXL-JOB中&#xff0c;有一个xxl-job-admin项目&#xff0c;这个就相当于定时任务的调度平台&#xff0c;我们参考XXL-JOB&#xff0c;也添加这么一个调度平台&#xff0c;由于篇幅有限&#xff0c;我们先实现一个本地的定时任务调度平台&#xff0c;至于如何调用远程的…
阅读更多...
网络工程师----第二十八天

网络工程师----第二十八天

计算机基础 第五章&#xff1a;运输层 运输层的两个协议&#xff1a; 1、传输控制协议TCP&#xff1a; TCP最主要的特点&#xff1a; (1)TCP是面向连接的。应用程序在使用TCP协议之前&#xff0c;必须先建立连接。在传送数据完毕后&#xff0c;必须释放已经建立的TCP连接。…
阅读更多...
开源收银系统在服装连锁店中发挥的重要作用

开源收银系统在服装连锁店中发挥的重要作用

在当今竞争激烈的零售市场中&#xff0c;服装连锁店面临着日益复杂的经营环境和多样化的消费需求。在这样的背景下&#xff0c;开源收银系统成为了服装连锁店管理的关键利器。该系统不仅提供了高效的收银功能&#xff0c;还涵盖了进销存管理、会员管理、门店补货等多方面功能&a…
阅读更多...
Github项目管理——仓库概述（一）

Github项目管理——仓库概述（一）

个人名片&#xff1a; &#x1f393;作者简介&#xff1a;嵌入式领域优质创作者&#x1f310;个人主页&#xff1a;妄北y &#x1f4de;个人QQ&#xff1a;2061314755 &#x1f48c;个人邮箱&#xff1a;[mailto:2061314755qq.com] &#x1f4f1;个人微信&#xff1a;Vir2025WB…
阅读更多...
【Cesium解读】Cesium中primitive/entity贴地

【Cesium解读】Cesium中primitive/entity贴地

官方案例 Cesium Sandcastle Cesium Sandcastle scene.globe.depthTestAgainstTerrain true; True if primitives such as billboards, polylines, labels, etc. should be depth-tested against the terrain surface, or false if such primitives should always be draw…
阅读更多...
7nm项目之模块实现——02 Placeopt分析

7nm项目之模块实现——02 Placeopt分析

一、Log需要看什么 1.log最后的error 注意&#xff1a;warnning暂时可以不用过于关注&#xff0c;如果特别的warning出现问题&#xff0c;在其他方面也会体现 2.run time 在大型项目实际开发中&#xff0c;周期一般较长&#xff0c;可能几天过这几周&#xff0c;所以这就需要…
阅读更多...
STK12 RPO模块学习 （1）

STK12 RPO模块学习 （1）

一、背景介绍 在STK12中&#xff0c;在Astrogator的模块上开发了新的模块&#xff08;Rendezvous and proximity operations)。轨道交会接近通常来说是一个很复杂的过程。RPO实现需要对轨道动力学有一个清晰的理解&#xff0c;并且对于Astrogator模块具备很强的背景和经验&…
阅读更多...
前端工程化 - 快速通关 - vue

前端工程化 - 快速通关 - vue

目录 npm 2.1环境 2.2命令 2.3使用流程 Vite 3.1简介 3.2实战 Vue3 4.1组件化 4.2SFC 4.3Vue工程 4.4基础使用 4.5进阶用法 4.6总结 npm npm 是 nodejs 中进行 包管理 的工具&#xff1b; 下载&#xff1a;Node.js — Run JavaScript Everywhere 2.1环境 ●安…
阅读更多...
基于fastapi sqladmin开发，实现可动态配置admin

基于fastapi sqladmin开发，实现可动态配置admin

1. 功能介绍&#xff1a; 1. 支持动态创建表、类&#xff0c;属性&#xff0c;唯一约束、外键&#xff0c;索引&#xff0c;关系&#xff0c;无需写代码&#xff0c;快速创建业务对象&#xff1b; 2. 支持配置admin显示参数&#xff0c;支持sqladmin原生参数设置&#xff0c;动…
阅读更多...
codeblock couldn‘t create project directory ：path

codeblock couldn‘t create project directory ：path

1.原因&#xff1a; 因为我使用的是mac虚拟机&#xff0c;所以路径跟window不太一样&#xff0c;可能导致codeblock找不到路径&#xff0c;所以无法创建。 2.换一个跟window文件路径相同的就好&#xff0c;例如 C:\programPractice\myProject\
阅读更多...
JavaEE之线程（5）——Java内存模型、内存可见性、volatile关键字

JavaEE之线程（5）——Java内存模型、内存可见性、volatile关键字

前言 volatile可以理解成轻量级的 synchronized&#xff0c; 它在多CPU开发中保证了共享变量的“可见性”&#xff0c;可见性我们可以理解成是&#xff1a;当一个线程修改一个共享变量时&#xff0c;另一个线程可以读到这个修改的值。由于它不会引起线程的上下文切换和调度&am…
阅读更多...
arp icmp 等报文格式

arp icmp 等报文格式

ARP报文格式 ARP是一个独立的三层协议&#xff0c;所以ARP报文在向数据链路层传输时不需要经过IP协议的封装&#xff0c;而是直接生成自己的报文&#xff0c;其中包括ARP报头&#xff0c;到数据链路层后再由对应的数据链路层协议&#xff08;如以太网协议&#xff09;进行封装…
阅读更多...
[第五空间 2021]WebFTP

[第五空间 2021]WebFTP

目录扫描git泄露phpinfo.php 一开始想到是sql注入&#xff0c;但是不行。目录扫描&#xff0c;发现 .git 和 phpinfo.php 访问phpinfo.php&#xff0c;ctrlf 搜索 flag&#xff0c;找到 flag。
阅读更多...
Pyqt中QThread传递自己定义的参数、类、函数

Pyqt中QThread传递自己定义的参数、类、函数

Pyqt中QThread传递自己定义的参数、类、函数 1 pyqt中Qthread传递自己定义的参数2 pyqt中Qthread传递自己定义的类3 pyqt中Qthread传递自己定义的函数4 pyqt中Qthread内部定义自己的函数5 pyqt中Qthread传递参数到内部定义自己的函数 1 pyqt中Qthread传递自己定义的参数 在PyQ…
阅读更多...
选择法（数值排序）（C语言）

选择法（数值排序）（C语言）

一、运行结果&#xff1b; 二、源代码&#xff1b; # define _CRT_SECURE_NO_WARNINGS # include <stdio.h>//声明排序函数sort; void sort(int a[], int n);int main() {//初始化变量值&#xff1b;int i, a[10];//填充数组&#xff1b;printf("请输入10个整数\n&…
阅读更多...
C语言错题本之＜结构体＞

C语言错题本之＜结构体＞

以下叙述中正确的是________. A)预处理命令行必须位于源文件的开头 B)在源文件的一行上可以有多条预处理命令 C)宏名必须用大写字母表示 D)宏替换不占用程序的运行时间 答案&#xff1a;D 解析&#xff1a; A&#xff1a;在C、C等编程语言中&#xff0c;预处理指令&#xff08;…
阅读更多...
轻松掌握抖音自动点赞技巧，快速吸粉

轻松掌握抖音自动点赞技巧，快速吸粉

在当今这个信息爆炸的时代&#xff0c;抖音作为短视频领域的领头羊&#xff0c;不仅汇聚了庞大的用户群体&#xff0c;也成为了品牌和个人展示自我、吸引粉丝的重要平台。如何在众多内容创作者中脱颖而出&#xff0c;实现高效引流获客&#xff0c;精准推广自己的内容&#xff0…
阅读更多...
springboot+vue+mybatis台球俱乐部管理系统的设计与实现+PPT+论文+讲解+售后

springboot+vue+mybatis台球俱乐部管理系统的设计与实现+PPT+论文+讲解+售后

随着信息技术在管理上越来越深入而广泛的应用&#xff0c;作为一般的台球厅都会跟上时代的变化&#xff0c;用上计算机来代表重复性的劳动&#xff0c;并且给用户一种新奇的感受&#xff0c;实现台球俱乐部系统 在技术上已成熟。本文介绍了台球俱乐部系统 的开发全过程。通过分…
阅读更多...
Jmeter＋Grafana＋Prometheus搭建压测监控平台

Jmeter＋Grafana＋Prometheus搭建压测监控平台

本文不介绍压测的规范与技术指标&#xff0c;本文是演示针对Jmeter如何将压测过程中的数据指标&#xff0c;通过Prometheus采集存储&#xff0c;并在Granfan平台进行仪表盘展示; 介绍 系统压测属于日常项目开发中的一个测试环节&#xff0c;使用测试工具模拟真实用户行为&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023