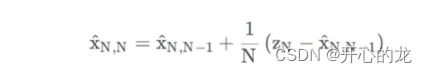通过一个例子来引出卡尔曼滤波的状态更新方程;
这里系统状态是金条的重量;

为了估计系统的状态,我们可以多次测量金条的重量,然后求平均值;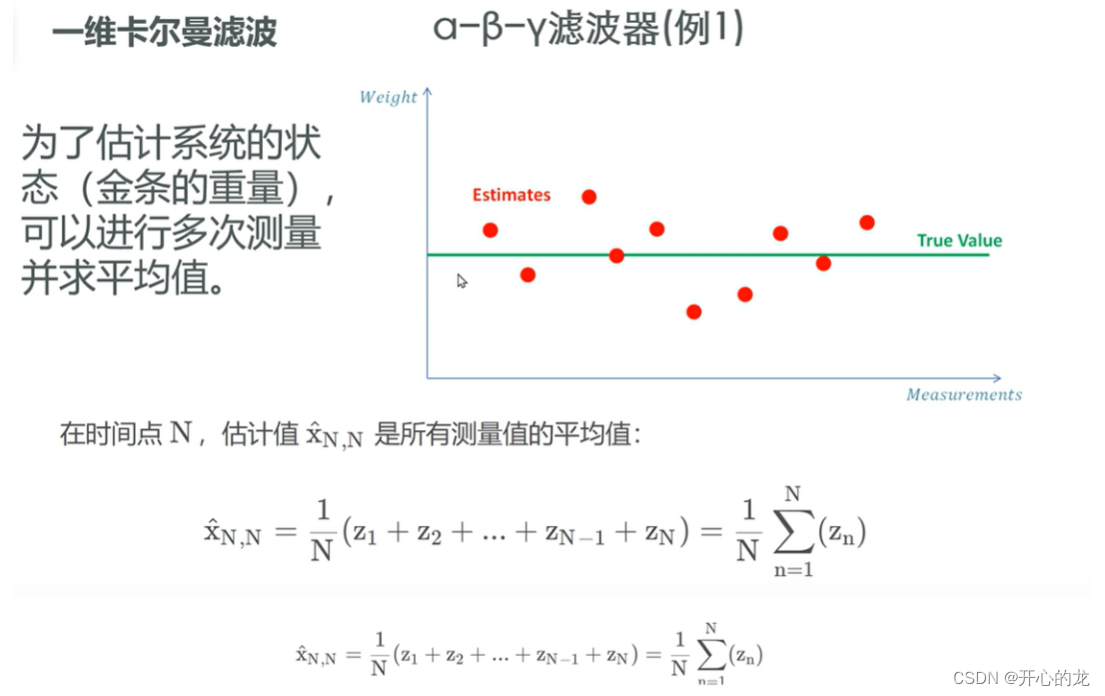
其中估计值是所有测量值的平均值;

由于我们使用的是静态模型(金条的重量是不会在短时间内发生改变的),所以第N次的估计值和N+1次的估计值相等,即




具体的物理意义:
1.预测重量的调整:表示测量值Zn和先验估计值(测出第N-1次后,对第N次的估计)之间的差异,称为残差或者创新,这个差异代表了当前的测量值和先前预测的偏差;

加权平均:通过乘以权重因子,滤波器调整对这个差异的响应,较大的权重因子,表示更信任当前测量值,较小的权重因子表示更信任先前的预测;
更新后的估计位置:通过将加权的残值添加到预测重量,得到更新的后的估计重量,这意味着新的估计重量是预测重量和测量重量之间的加权平均,更加接近实际重量;
其中1/N随着测量次数越来越小,意味着开始时没有足够的重量信息,估算值主要依靠测量值,但是随着次数越来越多,每次测量的值在估计过程中占比也越来越少,随着迭代次数足够多,新的测量值对估计值的影响可以忽略不记;
在做第一次测量之前,可以通过看金条上刻的数字(或粗略估计)得到金条的重量,着称为初始猜测(Initial Guess),它将是我们的第一个估计;
这个估计并不会影响我们后面的结果,随着测量次数逐渐增大,最后估计的结果都会趋于真实值,这就是滤波器的厉害之处;
在卡尔曼滤波器中1/N这个权重因子就是卡尔曼增益 ;
这个方程的形式就是状态更新方程,如下:


状态更新方程只是卡尔曼滤波的一个方程,卡尔曼滤波是一个有机整体,具体流程如下:

流程并不是按照Step1.2.3进行的,具体如图所示:
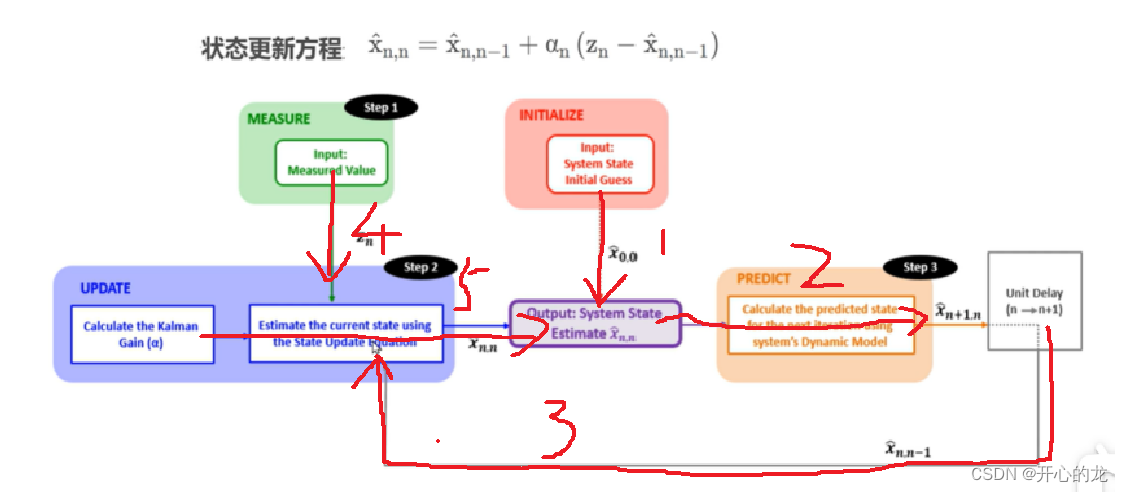
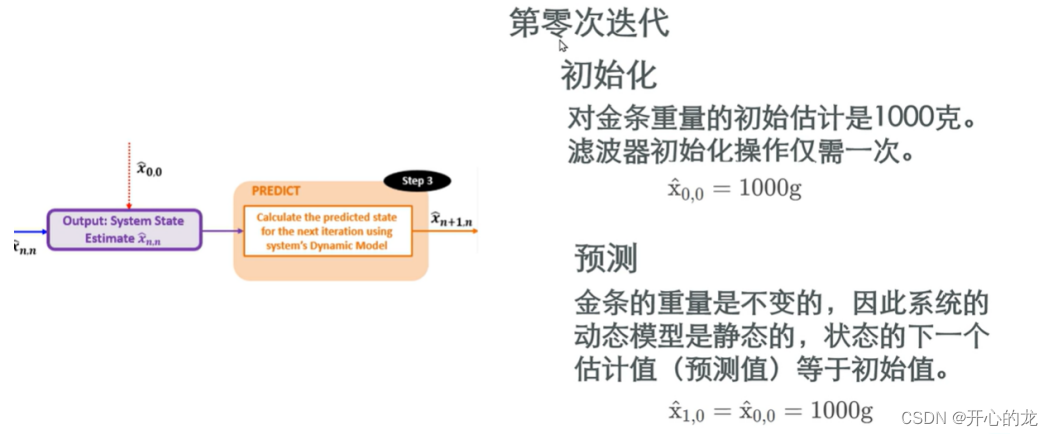
首先第一步1:进行初始化,我们根据各方面因素,输入一个估计值X(0,0)(主观定义);
第二步2:进行预测(状态外推方程),但是由于我们目前使用的是静态模型,所以预测前后结果保持不变,得到输出估计值为X(1,0)(表示先验估计值,第0次对第一次的估计,其值仍然等于X(0,0));
第三步3:变为下一时刻n->n+1,此时N=1;
第四步4:进行测量,输入测量值Z1;
第五步5:根据状态更新方程,更新数据得到下一时刻的估计值,之后(初始化只进行一次)进行预测,由于我们是静态模型,所以不需要进行任何预测,值保持不变,循环往复;
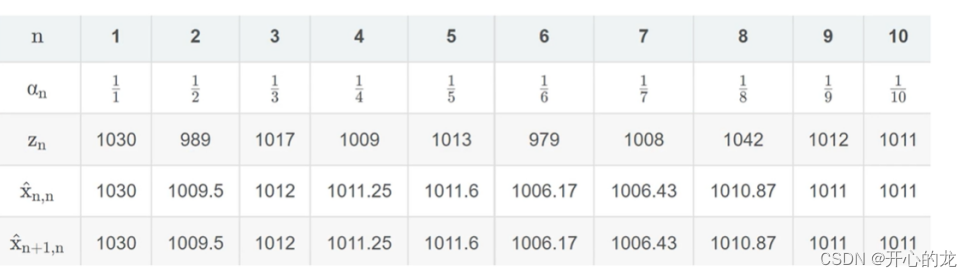
....经过十次后,得到以下结果:
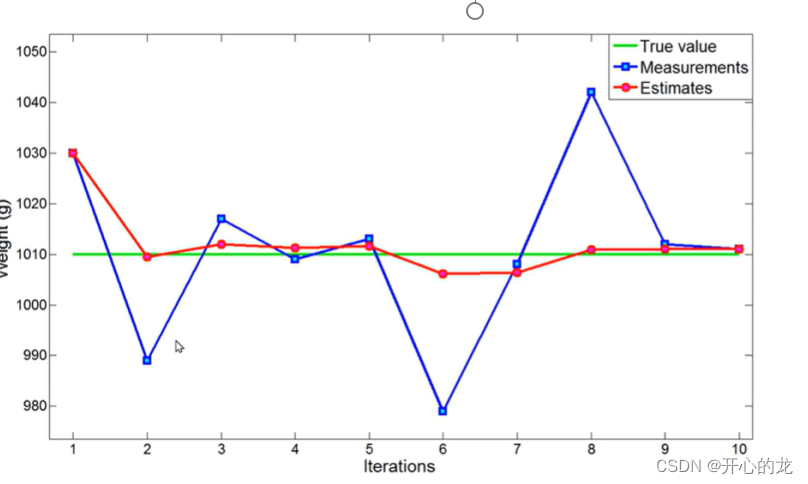
 绘制图像:绿色的线是真实值,蓝色的线是测量值,红色的线是估计值,随着迭代次数,估计值收敛于真实值;
绘制图像:绿色的线是真实值,蓝色的线是测量值,红色的线是估计值,随着迭代次数,估计值收敛于真实值;
具体举例:
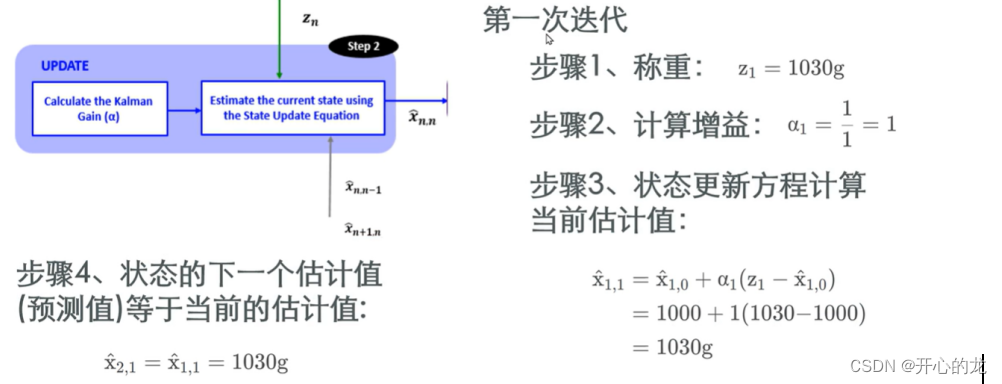 第二次迭代:
第二次迭代:
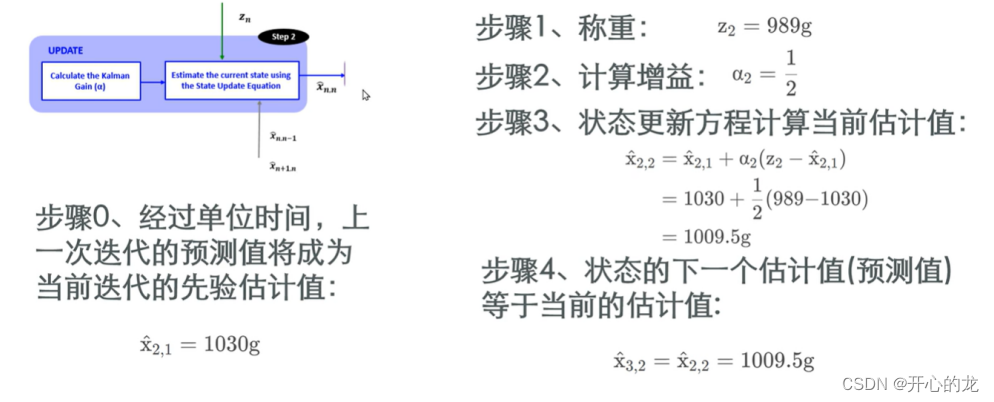
第三次迭代:
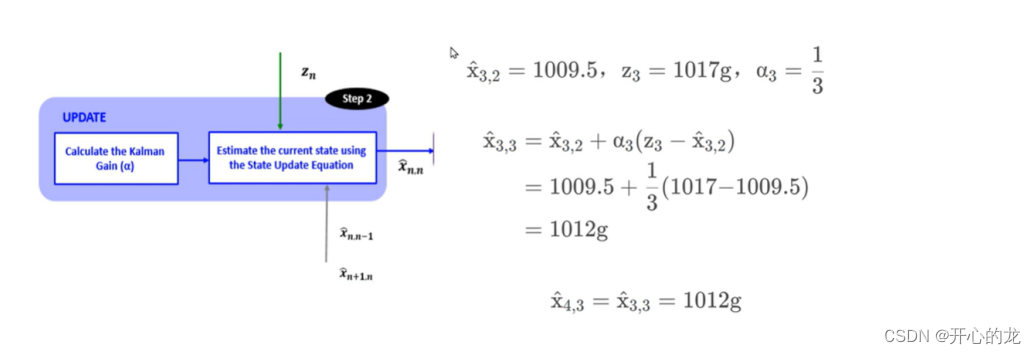 增益随着测量的次数而减小,每一次测量值的影响都比之前前一个测量值小;
增益随着测量的次数而减小,每一次测量值的影响都比之前前一个测量值小;
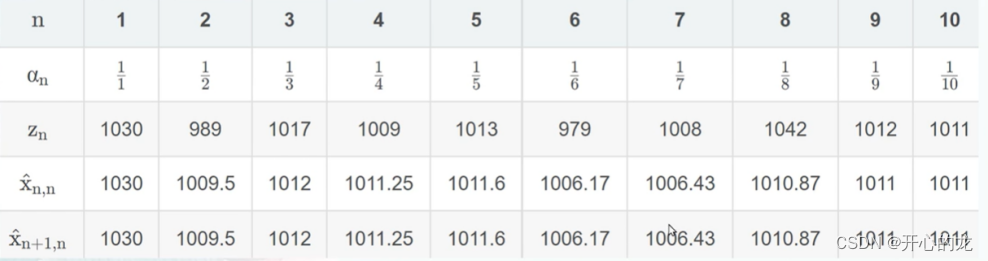
在这个例子中,我们为静态系统设计了一个简单的估计算法,并且推导出了卡尔曼滤波的五个方程之一的状态更新方程。
系统的输入是上一时刻的先验估计值和权重因子,输出是当前时刻的估计值;
表示通过预测值加上残差(测量值减去预测值)*权重因子得到当前时刻的估计值,更加接近实际重量;