个人主页：一代…
个人专栏：数据结构

在面试中我们经常会遇到有关链表的相关题目，面试官通常会对题目给出拓展

下面我就两个leetcode上的一个双指针的题目为例，并对其进行拓展

题目链接：环形链表

题目描述：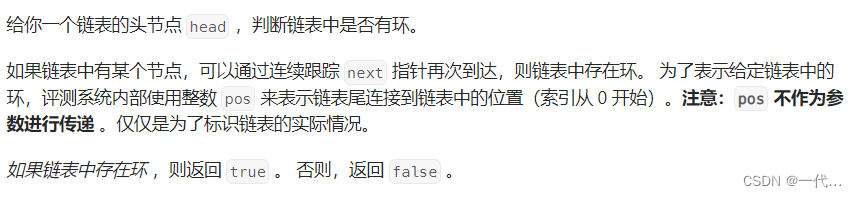
示例：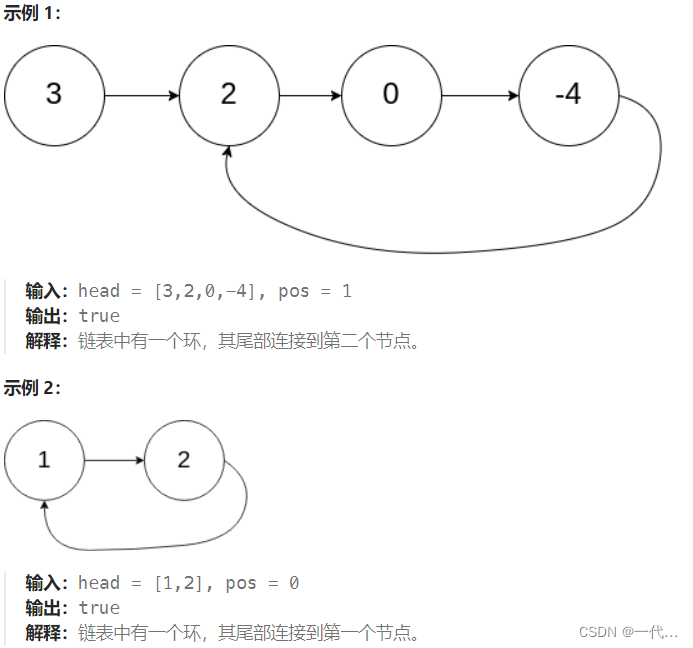

思路：运用快慢指针，快指针一次走两步，慢指针一次走一步，若链表带环，则快慢指针一定会在环中相遇，若不带环，则快指针就会走到末尾（NULL或最后一个节点）

代码示例：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode  ListNode;
bool hasCycle(struct ListNode *head) {
    ListNode* slow=head;
    ListNode* fast=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow)
        return true;
    }
    return false;
}

|

这里while循环中的fast&&fast->next不能调换顺序，因为当链表不带环，节点个数为偶数时，快指针会走到链表为空的位置，当fast->next在前，对空指针进行解引用，就会造成内存访问错误

（注：fast&&fast->next中如果前一个为假，那么整个表达式为假，就不会对下一个表达式进行计算）

拓展面试题目

在带环链表中，当slow每次走一步，fast每次走三步，那么slow会相遇吗？

slow每次走一步，fast每次走三步，那么当slow进环时，fast和slow相距的距离为N，那么没走一次，相距的距离就会减小2.
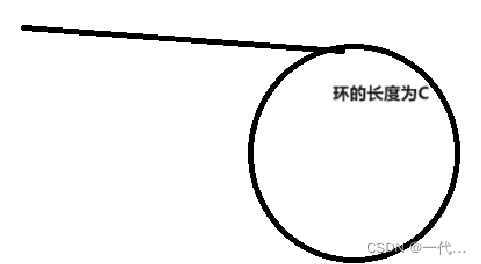
当链表长度为C时

于是就分为下面两种情况

总结：
1 当N为偶数时，slow和fast在第一轮就会相遇
2 当N为奇数时
C-1为偶数时就会在第二轮相遇
C-1为奇数时一定不会相遇（注：这种结论时错误的，这里下面会讲到）

为什么N是偶数，C时奇数这个条件一定不会成立呢？

假设：链表环之前长度为L,slow和fast相距的距离为N，slow进环时，fast已经在环中转了X圈

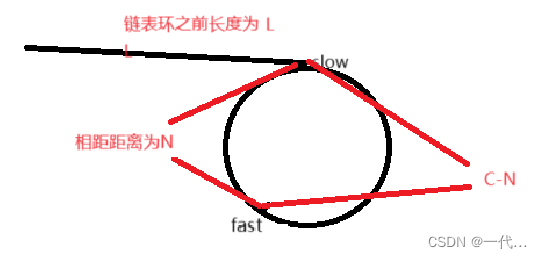
那么就会得出以下几个数学算式：
slow进环时，fast在环中转了X圈，于是fast走过的长度就为L+XC+C-N=L+(X+1)C-N，
slow走过的长度为L
又因为fast走过的长度为slow走过的长度的三倍，所以3L=L+(X+1)C-N
得出2L=(X+1)C-N
2L一定为偶数，当C为偶数，N为奇数时，由算式可得偶数=偶数-奇数，这显然时不出立的，于是就可得出把上面结论中当N为奇数，C-1为奇数时一定不可以追上的结论推翻，于是可证明当在环形链表中fast走3步，slow走1步时，fast和slow一定可以相遇，永远追不上的条件不成立

结论：
1 当N为偶数时，slow和fast在第一轮就会相遇
2 当N为奇数时，C-1为偶数时第一轮追不上，在第二轮就可以追上

题目链接：环形链表II

题目描述：
题目示例：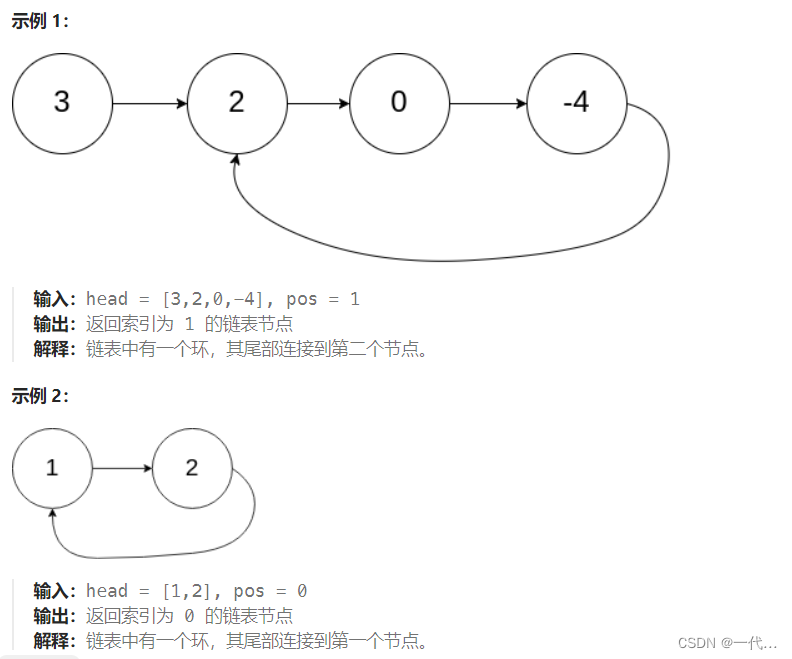
代码示例：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {
    ListNode *slow=head,*fast=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow)//相遇
        {
            ListNode *meet=slow;
            while(head!=meet)//相遇的节点即为入环的第一份节点
            {
                head=head->next;
                meet=meet->next;
            }
            return meet;
        }
    }
    return NULL;//无环
}

题目思路：定义一个快指针，一个慢指针，快指针一次走一步，慢指针一次走了两步，当两个指针相遇时节点为meet，在让头节点head从头开始走，一次走一步，meet从相遇的地点开始走，一次走一步，当两者相遇时即为入环的第一个节点

那么这是怎么得出来的呢？

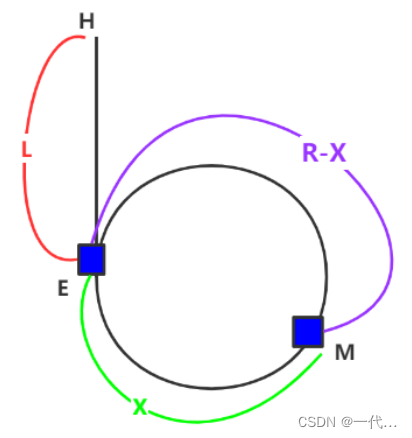
其中E为环的入口点，M为快慢指针的相遇点，L为环之前的链表的长度
由于从slow进环时在到与fast相遇，fast一定不会运动一个环的长度就可以追上slow
假设在slow到环入口时，fast已经转了N圈,环的长度为R
slow运动的距离为L+X
fast运动的距离为L+XR+X
L+NR+X=2L+2X
L=NR-X=R(N-1)+(R-X) (N=1,2,3,4…)
于是meet从相遇点开始走，head从头节点开始走，head走的长度为L,L=R(N-1)+(R-X) (N=1,2,3,4…),当head到入口E时，meet运动了R-X加上转了（N-1）圈的长度，则两者一定会相遇。