AVL树的完全指南：平衡与性能

文章目录

AVL树简介
AVL的操作
- 建立一个AVL树
- 插入操作
- 删除操作
书写代码
- 1.构造函数和析构函数
- 2.获取最大值和最小值
- 3.树的高度和节点个数
- 3.前序中序和后序遍历
- 4.判断树是否为空树
- 5.四个旋转操作
- 6.获取平衡因子
- 7.插入操作
- 8.删除操作
- 9.搜索节点
- .h文件中的定义
总结

在这里插入图片描述

AVL树简介

AVL树是一种自平衡的二叉搜索树，它的命名来源于其发明者 G. M. Adelson-Velsky 和 E. M. Landis。AVL树通过保持树的平衡性来提高搜索、插入和删除操作的效率。
在AVL树中，每个节点都有一个平衡因子，它表示节点的左子树高度与右子树高度的差值。平衡因子可以是-1、0或1，如果任何节点的平衡因子的绝对值大于1，则该树就不平衡，需要进行平衡调整。

AVL树本质也是一颗二叉查找树
但是在二叉查找树上加了平衡的概念，因为二叉查找树有很多限制的因素，当二叉查找树的节点呈线性分布的时候，整个二叉查找树就的效率就变成O(N)，所以在AVL树中就不存在不平衡的情况。

1.AVL树的特点：

左子树和右子树的高度差不大于1。
左子树和右子树的子树也是一颗AVL树

2.AVL树的相关概念

平衡因子：节点的平衡因子=左子树的高度-右子树的高度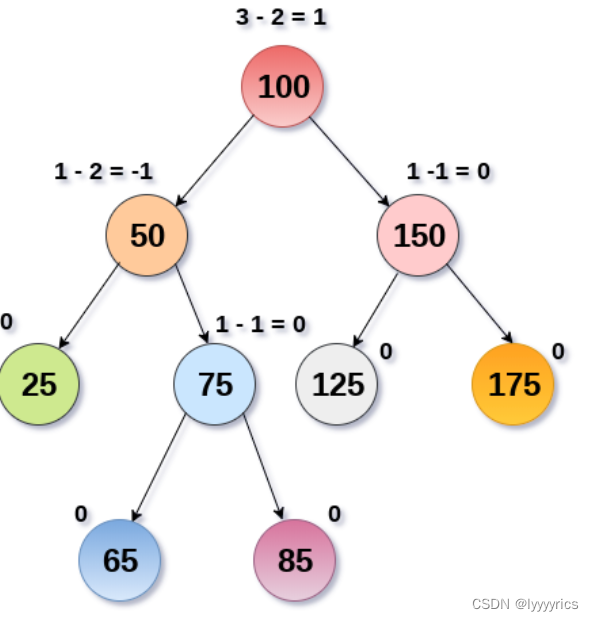
注意看上面的图上面的等式分别都代表了每个节点的平衡因子

3.AVL树对比普通二叉搜索树
2. 平衡性保证： AVL树保持了树的平衡性，即任何时刻树中任意节点的左右子树高度差不超过1。而普通的二叉搜索树可能会因为插入或删除操作而导致树的不平衡，从而影响了搜索、插入和删除操作的性能。

稳定的性能：由于AVL树的平衡性，搜索、插入和删除操作的时间复杂度始终保持在 O(log n) 的水平，其中 n 表示树中节点的数量。而普通的二叉搜索树在最坏情况下可能会退化成链表，导致搜索、插入和删除操作的时间复杂度上升至 O(n)。
高效的搜索操作： AVL树的平衡性保证了树的高度始终保持在较小的范围内，使得搜索操作非常高效。而普通的二叉搜索树可能会因为不平衡而导致搜索操作的性能下降。
快速的插入和删除操作： AVL树的自平衡性保证了插入和删除操作的高效性，使得这些操作的时间复杂度始终为 O(log n)。而普通的二叉搜索树在插入或删除节点后可能需要进行额外的平衡调整操作，导致性能下降。
适用于高性能需求的场景：由于AVL树在搜索、插入和删除操作上的高效性，它常被用作数据库中的索引结构，以提供快速的数据检索功能。而普通的二叉搜索树可能无法满足高性能的需求。

最直接的：
在这里插入图片描述

AVL的操作

建立一个AVL树

首先AVL树和二叉树一样，需要一个左子树和右子树的索引，还有需要一个存储值的关键字，除此之外，我们还需要保存当前节点的高度，因为在AVL树当中涉及到了高度之差，如果我们将当前节点的高度保存起来，就不用每次去计算了

代码：

class AVLNode
{
	friend class AVLTree;
public:

private:
	AVLNode* _left;
	AVLNode* _right;
	int _key;
	int _height;
};


class AVLTree
{
public:

private:
	AVLNode* _root;
};

**这里我们用两个类来定义AVL树，比较方便，一个类定义节点，一个类维护节点

插入操作

当当前节点的平衡因子为0的时候，下一个值随便怎么插入都不会影响平衡，而当当前节点的平衡因子等于1的时候，下一个值插入的位置就会影响当前节点的平衡了，插入操作一共分为四种情况，我们一一介绍：

1.右旋
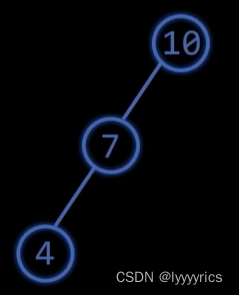
在这里插入图片描述

首先我们看上面这张图，当我们插入一个新的节点0时，很显然10的平衡因子是2，已经超过了AVL树定义的最大的平衡因子，所以，我们要对上面这颗树进行旋转让其满足AVL树的要求.
很显然，只需要将10右旋，然后让7作为10和4的新的父亲节点就可以了。
动图展示：
在这里插入图片描述

第二种需要右旋的情况：
在这里插入图片描述

这里只需要记住，，当我们要右旋时，冲突的右孩子作为新的左孩子就行了。
2.左旋

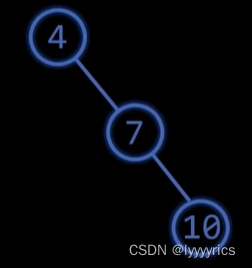
在这里插入图片描述
同样的，上面这个AVL树中的7的平衡因子的绝对值已经超过了1，所以应该对其进行旋转，由于4的平衡是-2,7的平衡因子是-1，，所以这种情况也被称之为RR型，对于这种RR型我们只需要对其进行一次右旋就可以解决问题了。
动图展示：
在这里插入图片描述
还有一种复杂的清情形：

先右旋再左旋

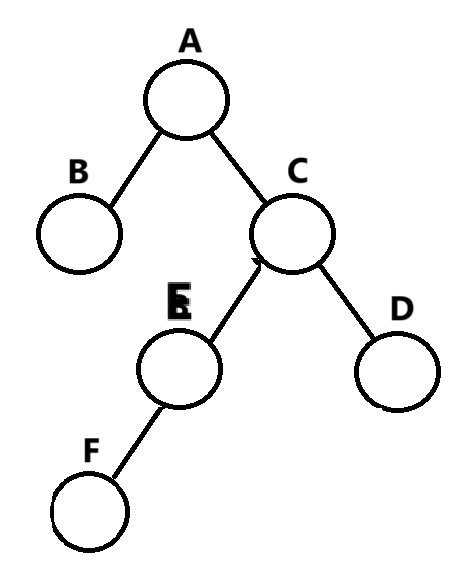
对于上面的AVL树，E是新插入的节点，首先这颗树的A节点的平衡因子是-2，然后就是C的平衡因子是1，这种情况我们把它叫做RL型，只需要对平衡因子是1的节点先进行右旋，然后再对平衡因子是A的节点进行左旋就可以了。

先左旋再右旋
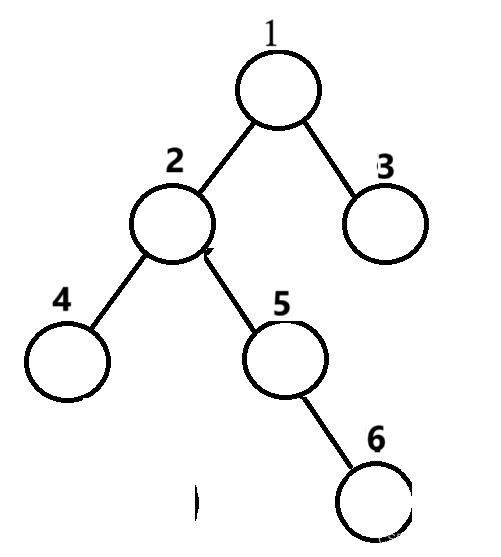
在这里插入图片描述

6是最后插入的节点对于这种情况，1的平衡因子是2，而2的平衡因子是-1.这种情况被称为是LR型，只需要先对平衡因子为-1的节点先左旋，然后再对平衡因子是2的节点进行右旋即可。

删除操作

删除操作和插入操作类似，再每次删除之后都要对祖先节点的平衡因子进行检查。

书写代码

1.构造函数和析构函数

//构造函数
AVLTree::AVLTree(AVLNode* root) :_root(root) {}

//析构函数
AVLTree::~AVLTree()
{
	clear(_root);
}
void AVLTree::clear(AVLNode* node)
{
	if (node == nullptr)
	{
		return;
	}
	clear(node->_left);
	clear(node->_right);
	delete node;
}

2.获取最大值和最小值

//获取最小值
int AVLTree::getMin()
{
	if (_root == nullptr)
	{
		return INT_MIN;
	}
	AVLNode* root = _root;
	while (root->_left != nullptr)
	{
		root = root->_left;
	}
	return root->_key;
}

//获取最大值
int AVLTree::getMax()
{
	if (_root == nullptr)
	{
		return INT_MAX;
	}
	AVLNode* root = _root;
	while (root->_right != nullptr)
	{
		root = root->_right;
	}
	return root->_key;
}
//函数重载，用于返回节点
AVLNode* AVLTree::getMin(AVLNode* node)
{
	if (node == nullptr)
	{
		return nullptr;
	}
	while (node->_left != nullptr)
	{
		node = node->_left;
	}
	return node;
}

3.树的高度和节点个数

//获取AVL树的节点的个数
int AVLTree::AssistgetSize(AVLNode* root)
{
	if (root == nullptr)
	{
		return 0;
	}
	return AssistgetSize(root->_left) + AssistgetSize(root->_right) + 1;
}
int AVLTree::getSize()
{
	return AssistgetSize(_root);
}
//获取高度
int AVLTree::getHeight()
{
	return AssistgetHeight(_root);
}
int AVLTree::AssistgetHeight(AVLNode* root)
{
	if (root == nullptr)
	{
		return 0;
	}
	return root->_height;
}

3.前序中序和后序遍历

//中序遍历
void AVLTree::AssistinOrderTraversal(AVLNode* _root)
{
	if (_root == nullptr)
	{
		return;
	}
	AssistinOrderTraversal(_root->_left);
	cout << _root->_key << ' ';
	AssistinOrderTraversal(_root->_right);
}
void AVLTree::inOrderTraversal()
{
	AssistinOrderTraversal(_root);
}

//前序遍历
void AVLTree::preOrderTraversal()
{
	AssistpreOrderTraversal(_root);
}
void AVLTree::AssistpreOrderTraversal(AVLNode* root)
{
	if (root == nullptr)
	{
		return;
	}
	cout << root->_key << ' ';
	AssistpreOrderTraversal(root->_left);
	AssistpreOrderTraversal(root->_right);
}
//后序遍历
void AVLTree::AssistpostOrderTraversal(AVLNode* root)
{
	if (root == nullptr)
	{
		return;
	}
	AssistpostOrderTraversal(root->_left);
	AssistpostOrderTraversal(root->_right);
	cout << root->_key << ' ';
}
void AVLTree::postOrderTraversal()
{
	AssistpostOrderTraversal(_root);
}

4.判断树是否为空树

//判空
bool AVLTree::isEmpty()
{
	return _root == nullptr;
}

5.四个旋转操作

/左旋
void AVLTree::leftRotate(AVLNode*& node)
{
	AVLNode* right = node->_right;
	node->_right = right->_left;
	right->_left = node;
	node = right;
}
//右旋
void AVLTree::rightRotate(AVLNode*& node)
{
	AVLNode* left = node->_left;
	node->_left = left->_right;
	left->_right = node;
	node = left;
}
//先右旋再左旋
void AVLTree::rightleftRotate(AVLNode*& node)
{
	rightRotate(node->_right);
	leftRotate(node);
}
//先左旋再右旋
void AVLTree::leftrightRotate(AVLNode*& node)
{
	leftRotate(node->_left);
	rightRotate(node);
}

6.获取平衡因子

int AVLTree::getbalance(AVLNode* root)
{
	return AssistgetHeight(root->_left) - AssistgetHeight(root->_right);
}

7.插入操作

AVLNode* AVLTree::AssistInsert(int key, AVLNode*& node)
{
	if (node == nullptr)
	{
		node = new AVLNode(key, nullptr, nullptr);
		return node;
	}
  	else if (node->_key > key)
	{
		AssistInsert(key, node->_left);
		//判断平衡因子是否是2，判断是LL型还是LR型
		if (getbalance(node) == 2)
		{
			//LL
			if (getbalance(node->_left) == 1)
			{
				//右旋
				rightRotate(node);
			}
			//LR
			else
			{
				//先左旋再右旋
				leftrightRotate(node);
			}
		}
	}
	else if (node->_key < key)
	{
		//向右边插入
		AssistInsert(key, node->_right);
		//如果是-2，那就是RR型或者是RL型
		if (getbalance(node) == -2)
		{
			//RR
			if (getbalance(node->_right) == -1)
			{
				//左旋
				leftRotate(node);
			}
			//RL
			else
			{
				//先右旋再左旋
				rightleftRotate(node);
			}
		}
	}
	node->_height = max(AssistgetHeight(node->_left), AssistgetHeight(node->_right)) + 1;
	return node;
}

void AVLTree::Insert(int key)
{
	_root = AssistInsert(key, _root);
}

8.删除操作

AVLNode* AVLTree::Assistremove(int key, AVLNode*& node)
{
	if (node == nullptr)
	{
		//空节点不需要删除直接返回nullptr
		return nullptr;
	}
	//要删除的值小于当前节点的值
	if (node->_key > key)
	{
		//递归左子树
		node->_left = Assistremove(key, node->_left);
	}
	//删除值大于当前节点的值
	else if (node->_key < key)
	{
		//递归右子树
		node->_right = Assistremove(key, node->_right);
	}
	else
	{
		//1.左子树是空树，右子树和左子树都是空树
		if (node->_left == nullptr)
		{
			AVLNode* tmp = node->_right;
			delete node;
			return tmp;
		}
		//只有右子树是空树的时候
		if (node->_right == nullptr)
		{
			AVLNode* tmp = node->_left;
			delete node;
			return tmp;
		}
		//左子树和右子树都不是空树时
		else
		{
			//找到右子树的最小值节点
			AVLNode* min = getMin(node->_right);
			//赋值
			node->_key = min->_key;
			//将删除有左子树和右子树的节点转换为删除末尾的节点
			node->_right = Assistremove(min->_key, node->_right);
		}
	}
	node->_height = max(AssistgetHeight(node->_left), AssistgetHeight(node->_right)) + 1;
	int balance = getbalance(node);
	if (balance == 2)
	{
		if (getbalance(node->_left) == 1)
		{
			rightRotate(node);
		}
		else
		{
			leftrightRotate(node);
		}
	}
	else if (balance == -2)
	{
		if (getbalance(node->_right) == -1)
		{
			leftRotate(node);
		}
		else
		{
			rightleftRotate(node);
		}
	}
	return node;
}
void AVLTree::remove(int key)
{
	_root = Assistremove(key, _root);
}

9.搜索节点

//搜索
bool AVLTree::search(int key, AVLNode* node)
{
	if (node == nullptr)
	{
		return false;
	}
	if (node->_key == key)
	{
		return true;
	}
	if (node->_key > key)
	{
		return search(key, node->_left);
	}
	else
	{
		return search(key, node->_right);
	}
}
bool AVLTree::search(int key)
{
	return search(key, _root); 
}

上面的代码对照着图理解更容易理解

.h文件中的定义

class AVLNode
{
	friend class AVLTree;
public:
	AVLNode(int key, AVLNode* left, AVLNode* right, int hight = 0)
	{
		_key = key;
		_left = left;
		_right = right;
		_height = hight;
	}
private:
	AVLNode* _left;
	AVLNode* _right;
	int _key;
	int _height;
};


class AVLTree
{
public:
	AVLTree(AVLNode* root = nullptr);
	~AVLTree();

	int getbalance(AVLNode* root);

	AVLNode* AssistInsert(int key, AVLNode*& node);
	void Insert(int key);

	void leftRotate(AVLNode*& node);
	void rightRotate(AVLNode*& node);
	void rightleftRotate(AVLNode*& node);
	void leftrightRotate(AVLNode*& node);

	AVLNode* Assistremove(int key, AVLNode*& node);
	void remove(int key);

	bool search(int key);
	bool search(int key, AVLNode* node);

	int getMin();
	AVLNode* getMin(AVLNode* node);
	int getMax();
	int AssistgetHeight(AVLNode* root);
	int getHeight();

	void inOrderTraversal();
	void AssistinOrderTraversal(AVLNode* _root);
	void preOrderTraversal();
	void AssistpreOrderTraversal(AVLNode* _root);
	void postOrderTraversal();
	void AssistpostOrderTraversal(AVLNode* _root);

	int getSize();
	int AssistgetSize(AVLNode* root);
	void clear(AVLNode* node);
	bool isEmpty();
private:
	AVLNode* _root;
};

总结

在本篇博客中，我们深入探讨了 AVL 树这一经典的数据结构。AVL 树作为一种自平衡的二叉搜索树，通过保持树的平衡性，提供了高效的搜索、插入和删除操作。我们从 AVL 树的基本概念出发，介绍了它的定义、特性和基本操作，包括旋转操作和平衡因子的概念。通过具体的例子和图示，我们深入理解了 AVL 树的工作原理和算法设计。

AVL 树之所以如此重要和受欢迎，主要是因为它在各种应用中都具有突出的优势。无论是作为数据库索引、编译器中的符号表还是操作系统中的文件系统，AVL 树都能够提供高效的数据检索功能，保证了程序的性能和效率。通过学习和掌握 AVL 树，我们不仅可以解决实际问题，提高程序的性能，还能够深入理解和应用其他复杂数据结构，为我们的编程技能和软件工程能力增添新的高度。

希望通过本篇博客的阅读，读者能够对 AVL 树有一个更加深入的理解，并且能够将其应用到实际的项目中去，为软件开发和数据处理带来更大的价值。感谢大家的阅读和支持！