1、背景介绍
由于点云无法精确刻画目标对象边缘信息,因此常规提取的边缘点直接相连所生成的轮廓线,锯齿现象显著,与真实情况相差甚远(图b所示)。
道格拉斯-普克(Douglas-Peuker)抽稀算法是用来对大量冗余的图形数据点进行压缩以提取必要的数据点。利用DP算法实现的轮廓线简化结果,如图c,其真实反应了点云形状。因此,在实际点云三维重建中,DP算法常用于点云简化,进而用于后续三维重建。
 | 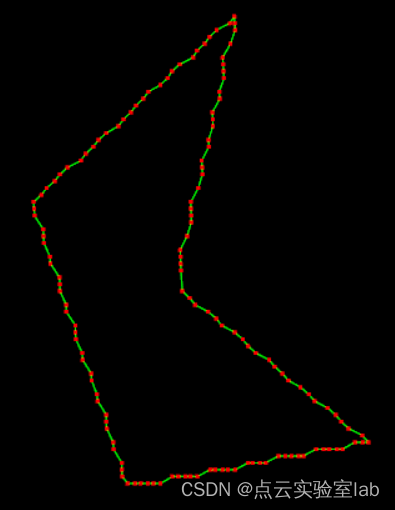 | 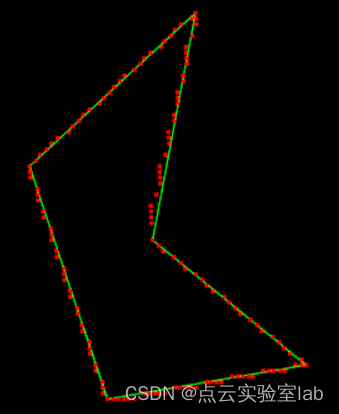 |
| (a)原始点云 | (b)边缘点直接相连 | (c)DP算法简化后轮廓 |
2、DP原理介绍
道格拉斯普克算法(Douglas-Peukcer)算法是一种简化线状要素的经典算法。对每一条曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大距离值dmax,用dmax与距离阈值D相比。若dmax<D,这条曲线上的中间点全部舍去;若dmax ≥D,保留dmax对应的坐标点,并以该点为界,把曲线分为两部分,对这两部分重复使用该方法。
算法的详细步骤如下:
(1) 在散点首尾两点间连一条直线,求出其余各点到该直线的距离(如图1、3、5中红色直线)。
(2) 选其最大者与阈值相比较,若大于阈值,则离该直线距离最大的点保留,否则将直线两端点间各点全部舍去(如图2相对图1中增加的点、图4相对图3增加的点)
(3) 依据所保留的点,将已知曲线分成两部分处理,重复第1、2步操作,迭代操作,即仍选距离最大者与阈值比较,依次取舍,直到无点可舍去,最后得到满足给定精度限差的点,舍去其他点,即完成线的化简。如图6中最终剩下的点。
 |  |
| (1) | (2) |
 |  |
| (3) | (4) |
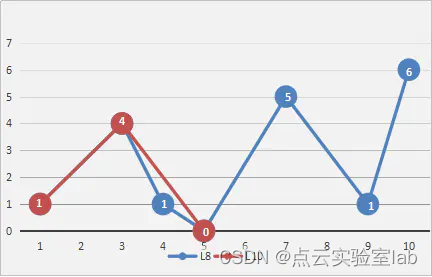 | 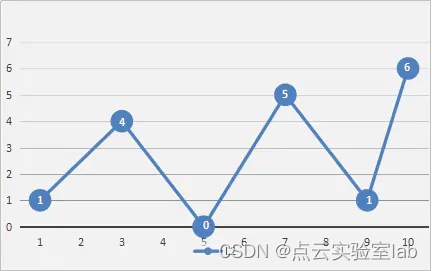 |
| (5) | (6) |
3、程序编程思想
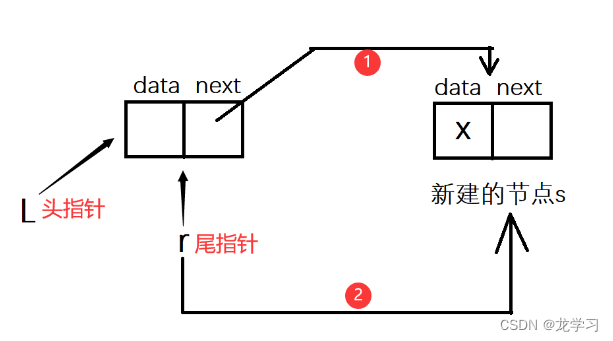
通过对DP算法原理介绍,发现该算法是一种递归思想,将点云一直划分成左右两部分,类似构建二叉树过程。首先对输入的一组点,判断其是否需要分组。

判断是否需要分组
当最大距离大于阈值时,需要进行划分成左右两部分(以4号点断开),如下图所示:

对于每一部分,采用上边类似的思想,判断递归下去,直至不再分成左右两棵树。
本程序编写过程:
3.1 边缘点提取
使用alpha shapes提取轮廓点,并对其进行排序,得到有序轮廓点
boundExtract(cloud, r, bound, non_bound);3.2 确定初始轮廓点分组
选取轮廓点中距离最远的两个点,依据这两个点确定是否需要将原始点进行分组。本程序采用x、y对应的最值(xmin、xmax、ymin、ymax)确定距离最远的两点。
GetTwoPointsMaxDis(bound, headpoint, endpoint, headindex, endindex);相距最远两点
其中划分组的策略如下:头部点对应的序列号(11)与尾部点序列号(62)之间的点(即11-62)化为一组,然后采62-93与1-11和起来分为一组。
3.3 对于每组点构造二叉树
通过对点分组,确定头、尾节点。再根据位于头尾节点中的点,确定待要划分的关键点。节点示意如下:
struct DPNode
{
pcl::PointXYZ HeadPoint;
pcl::PointXYZ EndPoint;
vector<pcl::PointXYZ> points;
DPNode *Left_node;//左边节点
DPNode *Right_node;//右边节点
bool NodeType;//该节点是否可以继续划分,若可以则是true,否则为false
};3.4 遍历二叉树寻找关键节点
采用前序遍历的方式(即先遍历左结点),找到关键点,关键节点为将点云划分为2组的点。
if (maxds < thres_ds)//小于阈值的,不再分割
{
root->Left_node = NULL;
root->Right_node = NULL;
root->NodeType = false;//不能再划分
}
else
{
root->NodeType = true;//可以继续划分
//将点划分成2部分,左边与右边
vector<pcl::PointXYZ> Leftpointsvec, Rightpointsvec;
for (int i = 0; i < points.size(); i++)
{
if (i <= maxindex)
{
Leftpointsvec.push_back(points[i]);//左边树包含的点
}
}
for (int i = 0; i < points.size(); i++)
{
if (i >= maxindex)
{
Rightpointsvec.push_back(points[i]);//右边树包含的点
}
}
//左边子树的头部点与尾部点
pcl::PointXYZ left_headpoint = headpoint;
pcl::PointXYZ left_endpoint = points[maxindex];
//右边子树的头部点与尾部点
pcl::PointXYZ right_headpoint = points[maxindex];
pcl::PointXYZ right_endpoint = endpoint;
//创建左、右树
root->Right_node = new DPNode();
BuildTree(root->Left_node, Leftpointsvec, left_headpoint, left_endpoint, thres_ds);
BuildTree(root->Right_node, Rightpointsvec, right_headpoint, right_endpoint, thres_ds);
}3.5 剔除重复关键点与排序
利用先序遍历,获取所有的关键点,即头、尾点,再对重复的关键点剔除,得到最终精简的轮廓关键点。
4、测试验证
根据上述原理,本程序基于PCL、C++进行实现。将“道格拉斯-普克 .cpp”文件放入原文件下,如下图所示:
cpp文件存放示意图
4.1 边缘提取测试
可以发现,两个点云数据中边缘点,均被成功提取出,其中红色点为边缘点,白色点为非边缘点。
 |  |
| 边缘提取示意图 | 边缘提取示意图 |
4.2 边缘点有序测试
直接将提取的边缘点进行相连,若能够刻画点云形状,则说明点云有序。如下图所示,虽然直接将点进行相连,锯齿现象比较明显,但是其仍大体刻画点云形状,证明提取的轮廓点为有序结构。
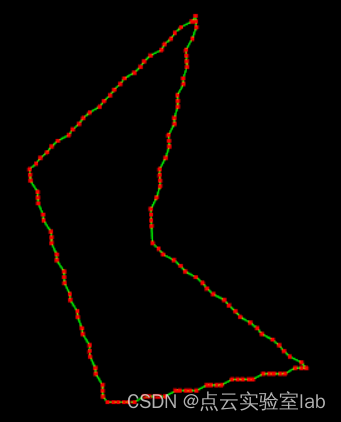 |  |
| 轮廓点相连 | 轮廓点相连 |
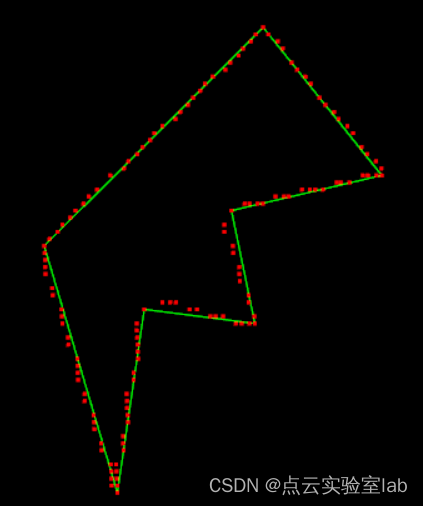
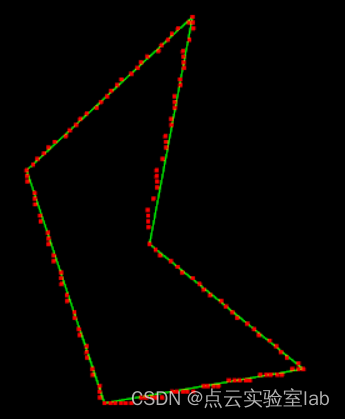
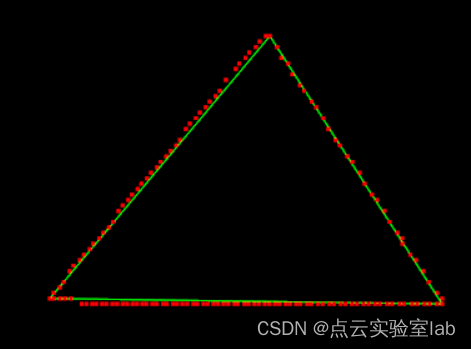
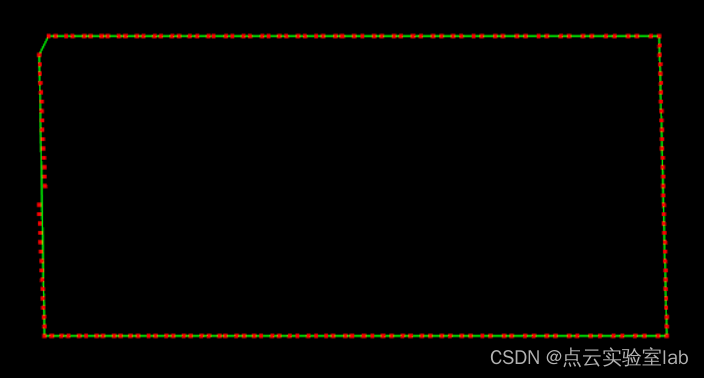
4.3 DP简化点云测试
使用各类不同形状的点云数据进行测试,可以发现点云边缘简化结果相当理想,比较简单,证明本程序能够正常运行,精简点云数据。
 |  |
 |  |
 |  |
5、小结
DP算法计算原理简单,精简点云效果理想,简化结果只与点到直线距离有关。理论上,当距离阈值设置越大,那么舍弃的点越多,关键点越少。因此,在实际使用过程中,需要根据需要设置参数。