1. 树的概念:
1. 树:由n个结点组成的有限集,有且只有一个根结点(由根结点可以访问后继结点),其他结点只有一个前驱结点,但可以有多个后继结点(一对多)。当n = 0时,为空树。
2. 叶子结点(终端结点):只有前驱结点没有后继结点;非叶子结点,即为分支结点。
3. 度:子结点的个数称之为度。
4. 树的度:树中各节点度的最大值。(默认为广度)
5. 深度:从根结点到最底层结点的层数。
6. 森林:n个互不相交的树的集合。
2. 二叉树的概念:
1. 二叉树:
任意一个结点的子结点个数不能超过2个(树的度为2),且子节点的位置不可更改(一旦改变位置,就是两个不一样的二叉树)。
2. 满二叉树:
在不增加树的层数的前提下,无法再增加一个结点的二叉树。(叶子结点处在同一层,除了叶子结点以外,其余所有的结点的度都为2)
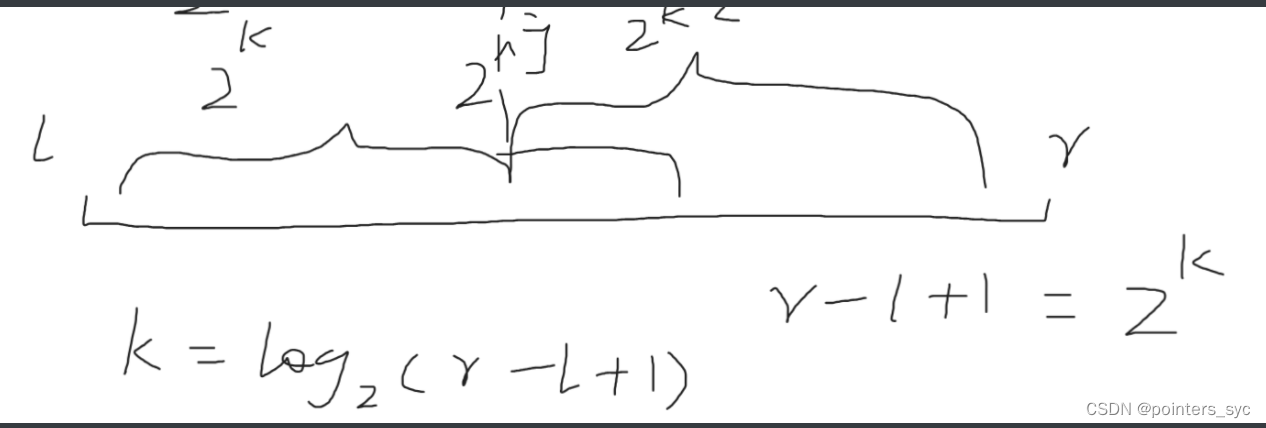
特性:满二叉树第k层有2^(k-1)个结点,k层满二叉树总共有2^k-1个结点。
练习:总结点为4847,求叶子结点为多少?
首先:2^12 - 1 = 4096 - 1 = 4095, 即可以推断出有13层,即4847 - 4095 = 752个
但第12层有:2^11 = 2048个,非叶子结点有752 / 2 = 376个
所以叶子结点:2048 - 376 + 752 = 2424个
3. 完全二叉树:
只是删除了满二叉树最底层最右边的连续若干个结点,形成了完全二叉树。
注意:1. 满二叉树是完全二叉树,但完全二叉树不一定是满二叉树。
2. 在满二叉树的基础上,如果要增加结点只能从上至下,从左至右的增加结点;如果要减少结点,只能从下至上,从右至左的删除结点。
3. 二叉树的遍历:
主要研究一对多的树形结构存储到一对一的线性存储单元中:
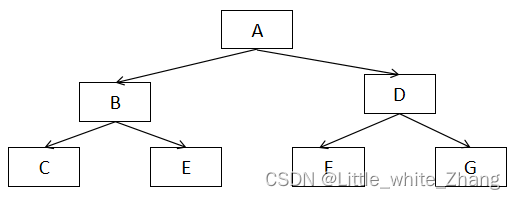
1. 前序遍历:先遍历根节点,再遍历左子树,最后遍历右子树(上图ABCEDFG)
2. 中序遍历:先遍历左子树,再遍历根节点,最后遍历右子树(上图CBEAFDG)
3. 后序遍历:先遍历左子树,在遍历右子树,最后遍历根节点(上图CEBFGDA)
4. 层序遍历:从上至下,从左至右,依次遍历(上图ABDCEFG)
注意:上诉前三种遍历方法为深度优化算法,第四种遍历方法为广度优先算法。
练习:
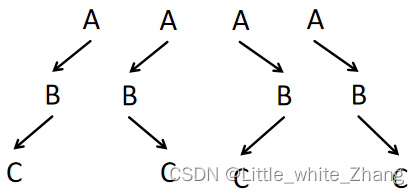
1. 如果只知道一个二叉树的前序遍历为ABC,求二叉树可能的情况:

2. 如果知道一个二叉树的前序遍历为ABC,后序遍历为CBA,求二叉树可能的情况:
3. 知道一个二叉树的前序遍历ABCEHDFG,中序遍历CBHEAFDG,求二叉树可能的情况:

4. 知道一个二叉树的中序遍历CBHEAFDG,后续遍历CHEBFGDA,求二叉树可能的情况:

从以上练习我们可以知道二叉树的遍历特性:如果只知道一个二叉树的前序遍历不能还原唯一的二叉树,知道前序遍历+后序遍历也不行,必须知道前序遍历+中序遍历,或者后序遍历+中序遍历才能得到唯一确定的一颗二叉树。
4. 二叉树的实现:
1. 二叉树的定义:
typedef char BTDATA_TYPE;
typedef struct tree_node
{
BTDATA_TYPE data;
struct tree_node *pl;
struct tree_node *pr;
}TREE_NODE;2. 二叉树的创建:
int idx = 0;
int cnt = 0;
char tree[] = {"ABC##EH###DF##G##"};
TREE_NODE *Create_BTree(void)
{
BTDATA_TYPE data = tree[idx++];
if(data == '#')
{
return NULL;
}
TREE_NODE *pnode = malloc(sizeof(TREE_NODE));
if(pnode == NULL)
{
perror("fail to malloc");
return NULL;
}
pnode->data = data;
pnode->pl = Create_BTree();
pnode->pr = Create_BTree();
return pnode;
}3. 二叉树的前序遍历:
void Pre_Order(TREE_NODE *proot)
{
if(proot == NULL)
{
return;
}
printf("%c", proot->data);
Pre_Order(proot->pl);
Pre_Order(proot->pr);
}4. 二叉树的中序遍历:
void Mid_Order(TREE_NODE *proot)
{
if(proot == NULL)
{
return;
}
Mid_Order(proot->pl);
printf("%c", proot->data);
Mid_Order(proot->pr);
}5. 二叉树的后序遍历:
void Pos_Order(TREE_NODE *proot)
{
if(proot == NULL)
{
return;
}
Pos_Order(proot->pl);
Pos_Order(proot->pr);
printf("%c", proot->data);
}6. 二叉树的层序遍历(结合前一篇的队列实现):
void Link_Layer_Order(TREE_NODE *proot)
{
QUEUE_LIST *pque = Create_Queue_List();
if(pque == NULL)
{
printf("fail to create queue list\n");
return;
}
QUEUE_NODE *pnode = Create_Queue_Node(proot);
if(pnode == NULL)
{
printf("fail to create queue node\n");
return;
}
DATA_TYPE outdata;
Push_Queue_Link(pque, pnode);
while(!Is_Empty_Queue(pque))
{
Pop_Queue_Link(pque, &outdata);
printf("%c", outdata->data);
if(outdata->pl != NULL)
{
pnode = Create_Queue_Node(outdata->pl);
Push_Queue_Link(pque, pnode);
}
if(outdata->pr != NULL)
{
pnode = Create_Queue_Node(outdata->pr);
Push_Queue_Link(pque, pnode);
}
}
Destory_Queue(pque);
return;
}7. 获得二叉树的结点个数:
int Get_PTree_Node_Cnt(TREE_NODE *proot)
{
if(proot == NULL)
{
return 0;
}
return 1+Get_PTree_Node_Cnt(proot->pl) + Get_PTree_Node_Cnt(proot->pr);
}
8. 获得二叉树的层数:
int Get_PTree_Layer_Cnt(TREE_NODE *proot)
{
if(proot == NULL)
{
return 0;
}
int layl = Get_PTree_Layer_Cnt(proot->pl);
int layr = Get_PTree_Layer_Cnt(proot->pr);
return layl > layr ? layl+1 : layr+1;
}9. 销毁二叉树:
void Destroy_PTree(TREE_NODE *proot)
{
if(proot == NULL)
{
return;
}
Destroy_PTree(proot->pl);
Destroy_PTree(proot->pr);
free(proot);
}