目录
- 0.观前必读
- 1.递归
- 1.什么是递归?
- 2.为什么会用到递归?
- 3.如何理解递归?
- 4.如何写好一个递归?
- 2.概念乱斗:P
- 1.深度优先遍历 vs 深度优先搜索 && 宽度优先遍历 vs 宽度优先搜索
- 2.搜索 vs 暴搜
- 3.拓展搜索问题
- 3.回溯与剪枝
- 4.总结
- 1.递归 vs 深搜
- 2.迭代 vs 递归
- 3.前序遍历 vs 后序遍历
- 5.经验之谈
- 1.全局变量的优势
- 2.剪枝
- 3.回溯
- 6.记忆化搜索 VS 动态规划
- 1.思路是什么?
- 2.本质理解
- 3.问题思考 && 总结
0.观前必读
- 本篇为总结篇,建议看了后面的博文后,再来看本篇,会有不一样的感受哦~
1.递归
1.什么是递归?
- 函数自己调用自己
2.为什么会用到递归?
- 本质:解决一个问题时,出现相同的子问题
- 主问题 -> 相同的子问题
- 子问题 -> 相同的子问题
- ……
3.如何理解递归?
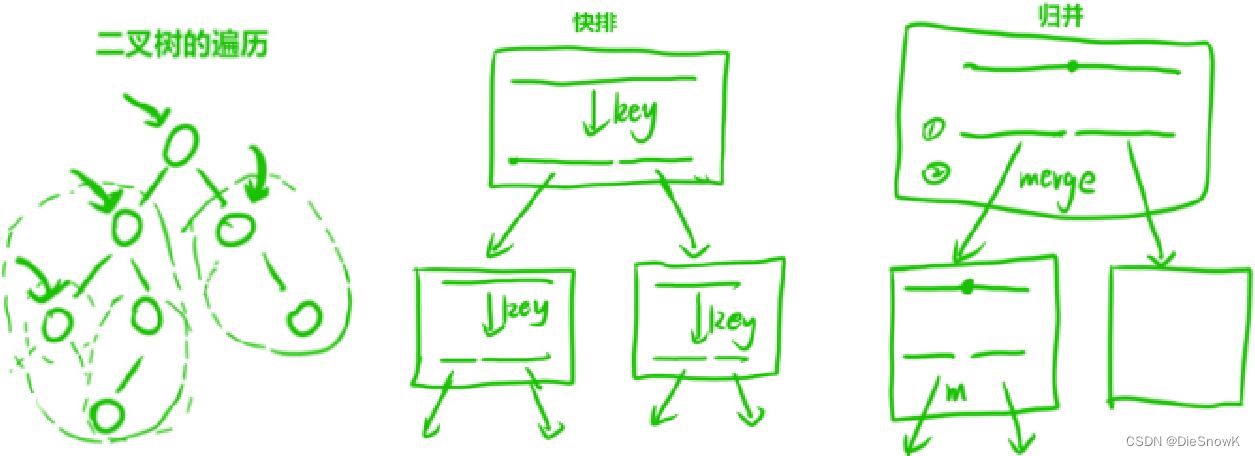
- 分为三个阶段
- 递归展开的细节图
- 二叉树中的题目
- 宏观看待递归的过程
- 不要在意递归的细节展开图
- 把递归的函数当成一个黑盒
- 相信这个黑盒一定能完成这个任务
- 用以下例子形象感受
// 二叉树的后序遍历
void DFS(TreeNode* root)
{
// 出口
if(root == nullptr)
{
return;
}
DFS(root->left); // 相信这个函数一定可以做到,遍历左子树
DFS(root->right); // 相信这个函数一定可以做到,遍历右子树
cout << root->val;
}
void Merge(vector<int>& nums, int left, int right)
{
// 出口
if(left >= right)
{
return;
}
int mid = left + (right - left) / 2;
Merge(nums, left, mid); // 相信这个函数一定可以做到,排序左区间
Merge(nums, mid + 1, right); // 相信这个函数一定可以做到,排序右区间
// Merge...
}
4.如何写好一个递归?
- 先写到相同的子问题
- 这将决定:函数头的设计
- 只关心某一个子问题是如何解决的
- 这将决定:函数体的书写
- 注意一下递归函数的出口
2.概念乱斗:P
1.深度优先遍历 vs 深度优先搜索 && 宽度优先遍历 vs 宽度优先搜索
- 搜索与遍历相比,只多了访问结点值这一步,所以可以这样认为
- 深度优先遍历 == 深度优先搜索
- 宽度优先遍历 == 宽度优先搜索
- 遍历是形式,目的是搜索
2.搜索 vs 暴搜
- 搜索:暴力枚举一遍所有的情况
- 搜索 == 暴搜
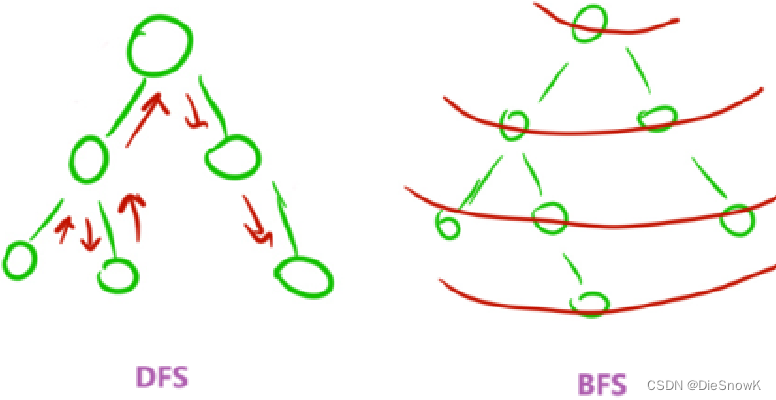
- BFS
- DFS
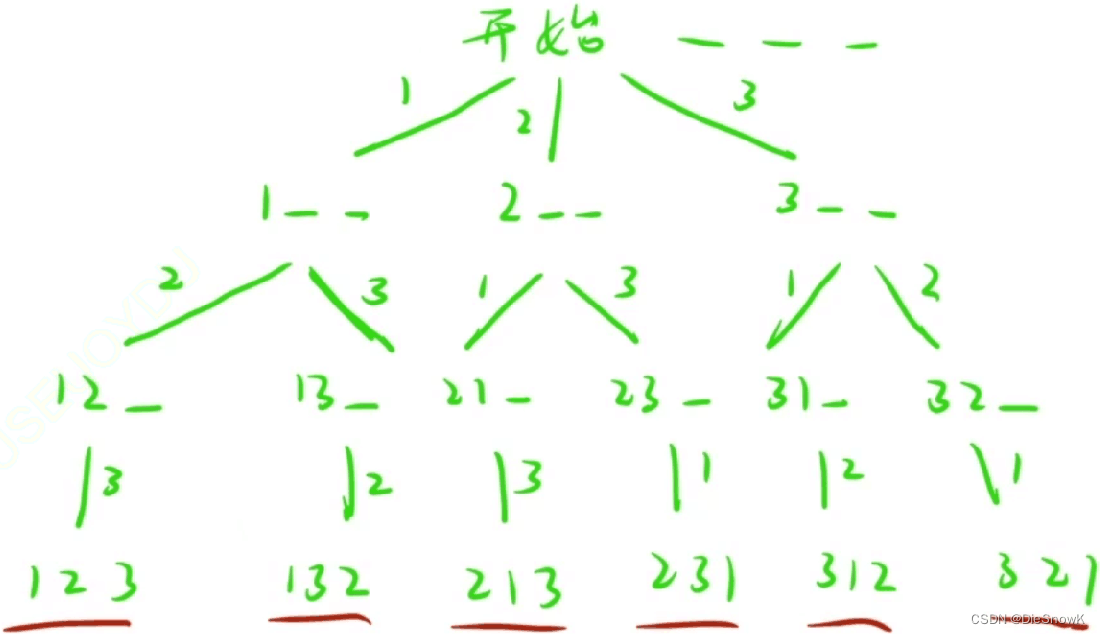
3.拓展搜索问题
- 全排列 <- 决策树
3.回溯与剪枝
- 回溯本质:深搜(DFS)
- 回退就是回溯,不用区分那么细
- 剪枝:在一个结点有两种选择,但是已经明确知道其中一种选择不是想要的结果,可以剪掉(去掉)这种结果/情况
- 在树中,就是形象的剪掉了一个叶子或者某一个结点的子树
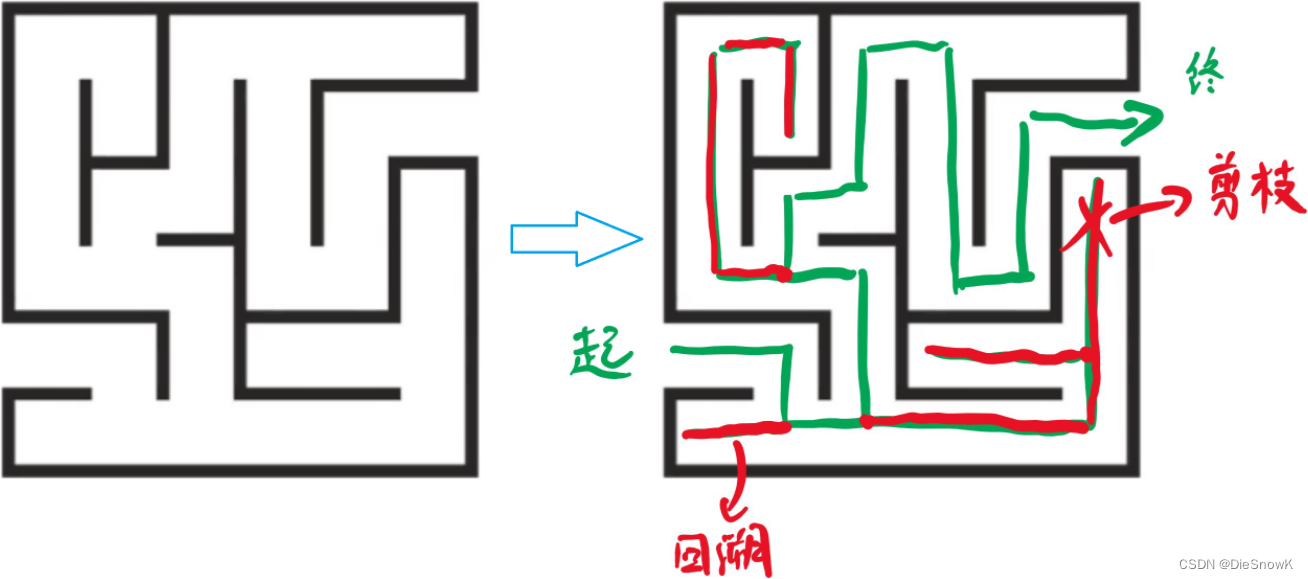
- 在树中,就是形象的剪掉了一个叶子或者某一个结点的子树
4.总结
1.递归 vs 深搜
- 递归的展开图,其实就是对一棵树做了一次深度优先遍历(DFS)
- 此处的树不局限于二叉树,多叉树也可以
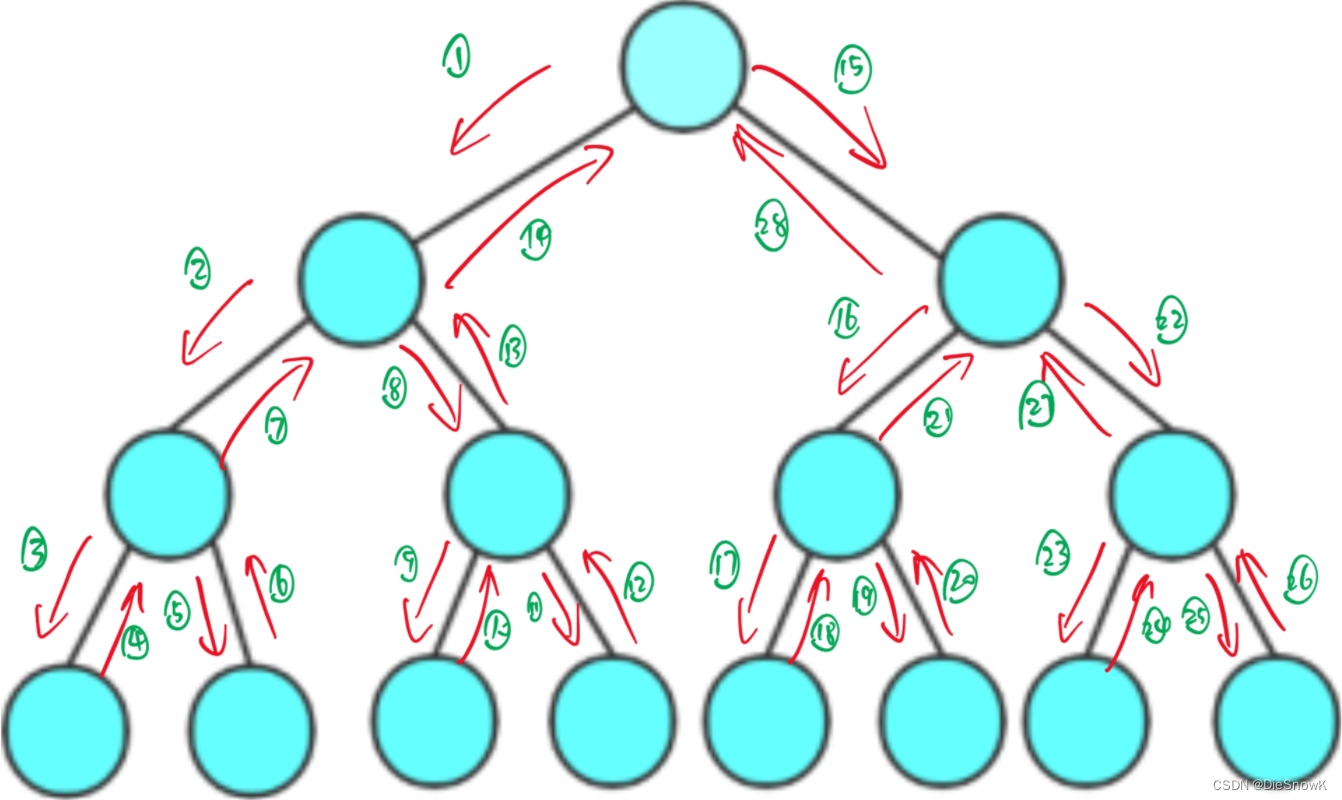
- 此处的树不局限于二叉树,多叉树也可以
2.迭代 vs 递归
-
本质:都是解决重复的子问题
-
迭代可以改递归,递归也可以改迭代
- 如果树的递归想改成迭代,需要借助栈来存储当前信息以帮助解决问题
- 因为树的递归时,当执行完左子树之后,整个函数是还没有被执行完的,还要进行后续操作,并且递归展开执行右子树的内容
- 所以当递归改成迭代时,就需要借助栈,来保存此时的信息,在完成"左子树"逻辑后,再进行后续操作
- 如果树的递归想改成迭代,需要借助栈来存储当前信息以帮助解决问题
-
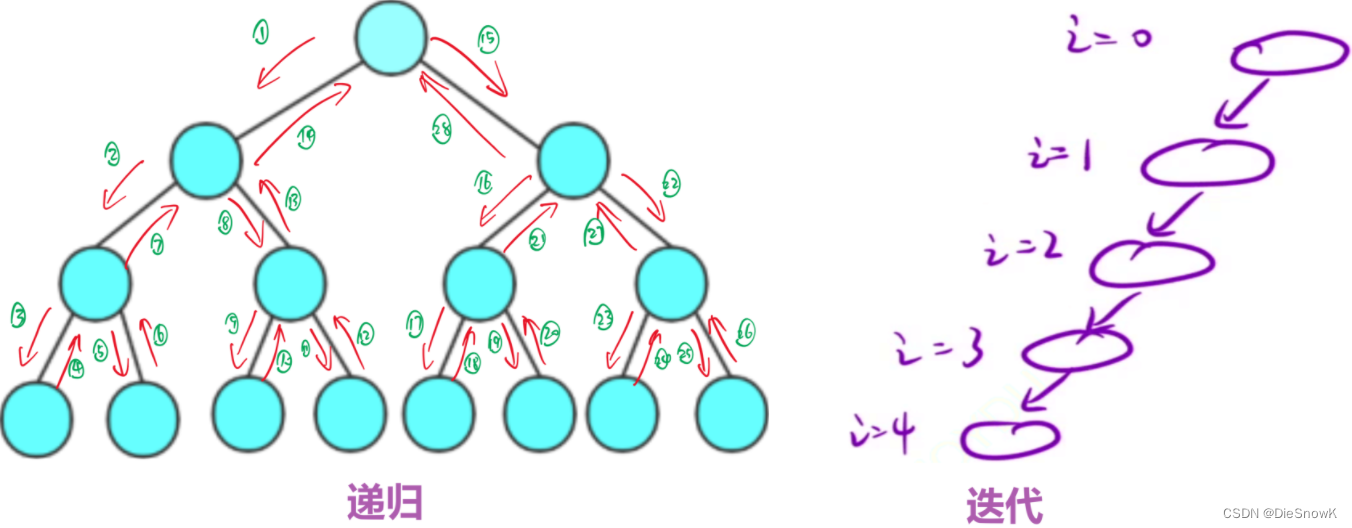
什么时候迭代舒服,什么时候递归舒服?
- 当递归展开图比较麻烦的时候,递归舒服
- 当递归展开图只有一个分支时,迭代舒服
-
用下面的代码感受下:如何遍历一个数组?
void ContainDuplicate(vector<int>& nums)
{
// 迭代
for(int i = 0; i < nums.size(); i++)
{
cout << nums[i] << " ";
}
// 递归
DFS(nums, 0);
}
void DFS(vector<int>& nums, size_t i)
{
if(i == nums.size())
{
return;
}
cout << nums[i] << " ";
DFS(nums, i + 1);
}
3.前序遍历 vs 后序遍历
- 补充:中序遍历是只在二叉树中才有的,多叉树是不适用的
- 前序遍历和后序遍历都是DFS,只是访问结点的时机不一样
- 以上面的遍历数组为例,可以看出前序遍历和后序遍历只是两行代码交换了一下顺序而已,本质就是访问结点的时机变了
void ContainDuplicate(vector<int>& nums)
{
// 迭代
for(int i = 0; i < nums.size(); i++)
{
cout << nums[i] << " ";
}
// 递归
DFS(nums, 0);
}
// 前序遍历
void DFS1(vector<int>& nums, size_t i)
{
if(i == nums.size())
{
return;
}
cout << nums[i] << " ";
DFS(nums, i + 1);
}
// 后序遍历
void DFS1(vector<int>& nums, size_t i)
{
if(i == nums.size())
{
return;
}
DFS(nums, i + 1);
cout << nums[i] << " ";
}
- 后序遍历按照左⼦树、右⼦树、根节点的顺序遍历⼆叉树的所有节点,通常⽤于⽗节点的状态依赖于⼦节点状态的题⽬
5.经验之谈
1.全局变量的优势
- 在解决递归问题时,全局变量有时会大大的简化递归模型的设计和问题的抽象
- 比如二叉树的中序遍历,全局变量就可以用来保存上一个访问的结点的状态值
- 此时,在中序遍历中,想把状态在每层递归中传递,就不会像前序遍历那样直接当成参数设计那样来的方便
2.剪枝
- 在判断此时条件已经不复合要求时,此时可以果断舍去后面的递归过程
- 因为此时已经知道结果,再往后继续递归展开判断也是没有意义的了
- 剪枝在递归中,可以加快搜索过程
- 具体感受可见「验证二叉搜索树」
3.回溯
- 理解顺序:回溯 -> 恢复现场
- 回溯:恢复现场,通常有两种做法
- 全局变量:一般是数组时使用比较好
- 函数传参:一般是单个变量时使用比较好
- 此时的回溯,是编译器/代码代为做了回溯,开销较小
6.记忆化搜索 VS 动态规划
1.思路是什么?
- 记忆化搜索:带备忘录的递归:P
- 动态规划一般思路:
- 确定状态表示 ->
dp[i]的含义 - 推导状态转移方程
- 初始化
- 确定填表顺序
- 确定返回值
- 确定状态表示 ->
2.本质理解
- 大部分情况下,记忆化搜索的代码是可以改成动态规划代码的
- 以斐波那契数列举例
- 确定状态表示:
dp[i]-> 第i个斐波那契数DFS()的含义
- 推导状态转移方程:
dp[i] = dp[i - 1] + dp[i - 2]DFS()的函数体
- 初始化:
dp[0] = 0, dp[1] = 1DFS()的递归出口
- 确定填表顺序:
- 填写备忘录的顺序
- 确定返回值:主函数是如何调用
DFS()的
- 确定状态表示:
- 动态规划和记忆化搜索本质
- 暴力解法 -> 暴搜
- 对递归解法的优化:把已经计算过的值,存起来
- 《算法导论》中,记忆化搜索和常规的动态规划都被归为动态规划的范畴,区别为:
- 记忆化搜索 -> 递归
- 常规的动态规划 -> 递推(循环)
3.问题思考 && 总结
-
所有的递归(暴搜,深搜),都可以改成记忆化搜索吗?
- 不能
- 只有在递归的过程中,出现了大量完全相同的问题时,才能用记忆化搜索的方式优化
-
带备忘录的递归 VS 带备忘录的动态规划 VS 记忆化搜索
- 都是一回事:P
-
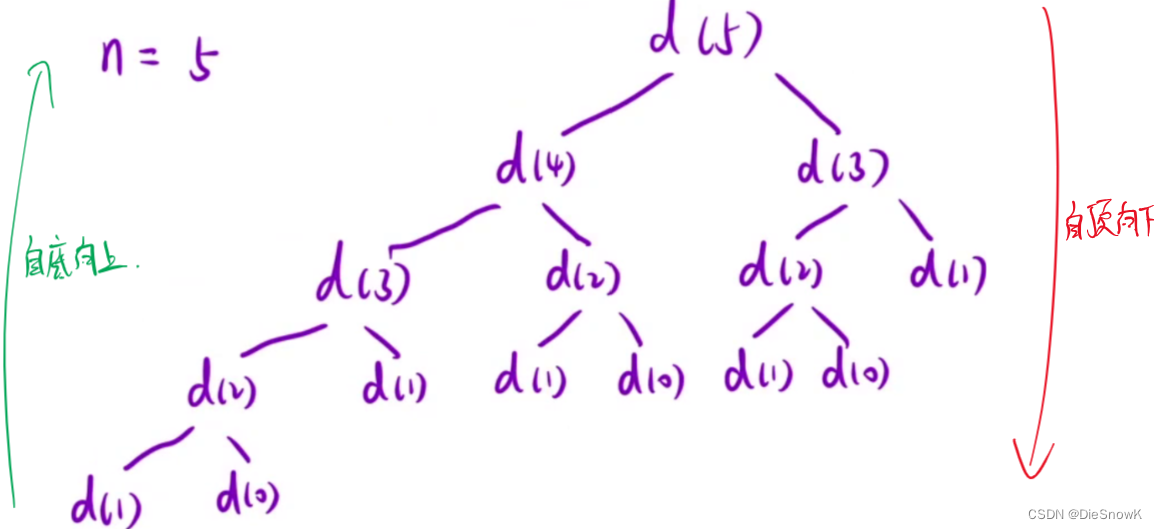
自顶向上 VS 自底向上
- 区别:解决问题时,不同的思考方式
- 自顶向下 -> 递归
- 自底向上 -> 动态规划
-
大多数情况下,暴搜 -> 记忆化搜索 -> 动态规划,这条优化代码的思考线路是没问题的
- 但是并不绝对,有时候直接思考动态规划比思考暴搜来的方便
- 因人而异,因题而异
- 总结:这条思考线路为我们确定状态表示,提供一个方向