小伙伴们大家好,我们又见面了,这次我们直接进入正题

时间复杂度的概念
时间复杂度的定义:在计算机科学中,
算法的时间复杂度是一个函数
,它定量描述了该算法的运行时间。一
个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知
道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个
分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,
算法中的基本操作的执行次数,为算法
的时间复杂度。
大家自行看一下即可,总之它是一个判断程序质量的参考标准,当然具体要求得看情况分析。
当然啦,如果你感觉定义太长,看不太懂或者不想看,可以看看我的大白话
时间复杂度解释(大白话)
时间复杂度是一个程序在计算机上运行所花费的时间,注意这个时间是没法人工计算的
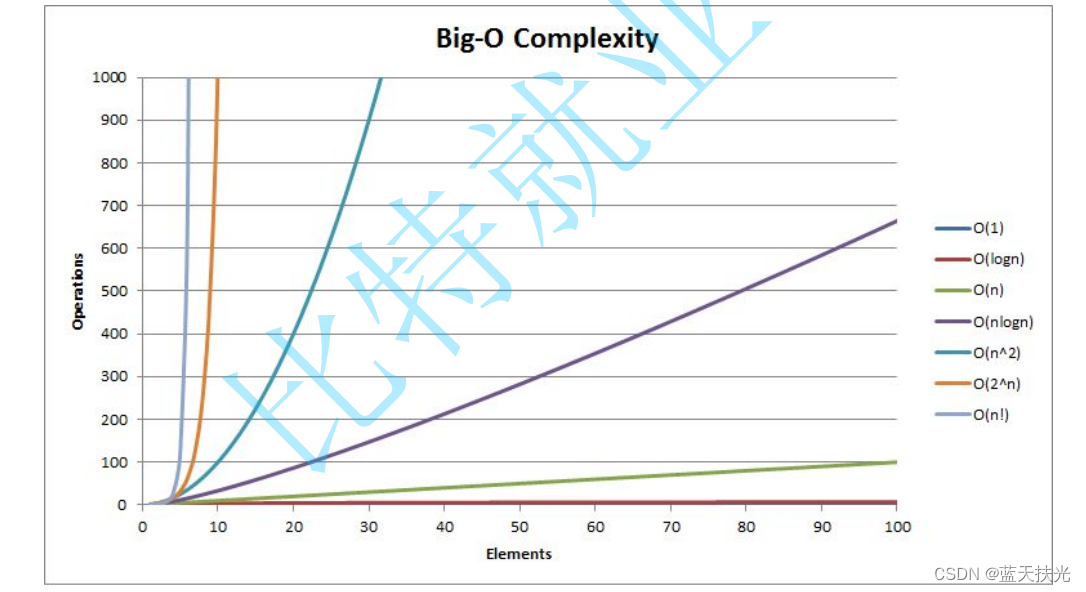
大O的渐近表示法
O(N)
这是基本格式。
推导大O阶法
1
、用常数
1
取代运行时间中的所有加法常数。
2
、在修改后的运行次数函数中,只保留最高阶项。
3
、如果最高阶项存在且不是
1
,则去除与这个项目相乘的常数。得到的结果就是大
O
阶。
那么我们来看个案例
大O阶法表示案例

请计算这串代码的时间复杂度(用大O阶法表示)。
解答: 首先看第一部分的循环,我们可以看到第一部分的循环是双循环,并且都是小于N,是的,这里我们要取出来的就是N,又因为这里的循环是双循环所以是N的二次方,即N^2。
第二部分的循环是单循环,并且小于2*N,也许有人就直接发言了,哦,我懂了,这里是取2*N吧,实则不然,这里我们取的是N,用大白话给大家解释一下,假设你有很多钱(∞),那么现在你给它翻一倍(也就是2*∞),请问它是否还是∞,所以乘上一个2根本不影响,所以忽略即可。
当然了,如果有常数项时,也需要忽略。
答案:O(N^2 + N)
当然啦,我也教一下怎么看是否是常数项。
怎么看是否是常数项
eg. for(int i = 0; i < 5; i++)
解答:O(5)
因此我们可以自己总结出规则。
大O阶法规则总结
1.有多重循环时,直接N^n次方
2.如果项前有系数,直接忽略
3.忽略常数项
通过上面我们会发现大
O
的渐进表示法
去掉了那些对结果影响不大的项
,简洁明了的表示出了执行次数。
时间复杂度的最好最坏以及平均情况
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数
(
上界
)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数
(
下界
)
例如:在一个长度为
N
数组中搜索一个数据
x
最好情况:
1
次找到
最坏情况:
N
次找到
平均情况:
N/2
次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为
O(N)
那么这里给大家放了两张表,有需要的同学可以自行保存
知识拓展
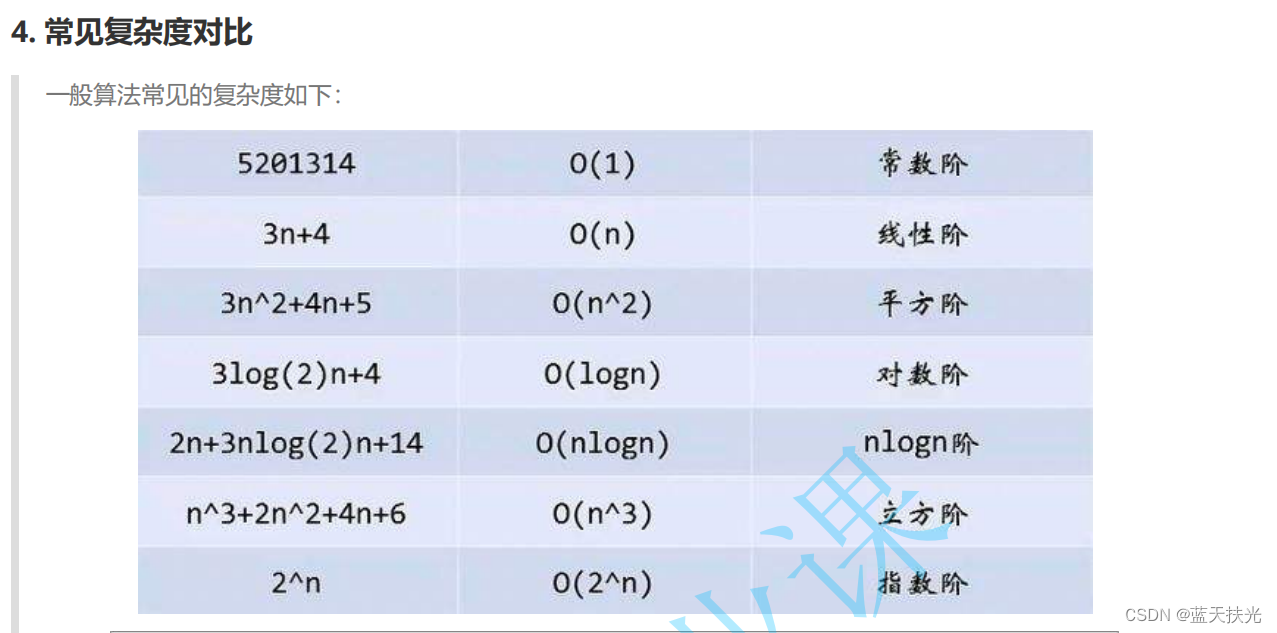
也许你会问,听了这么多,这玩意儿到底有什么用呢?
别急,今天我也给大家带来了相对应的例题讲解
时间复杂度例题讲解
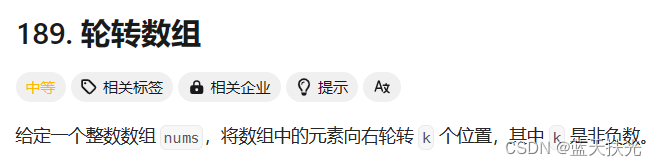

由题可知,我们需要将数组里的数字进行旋转,这里我给大家讲两个思路
例题思路
思路一:
将需要旋转的k个位置与数组元素个数进行取模,再通过循环,移动数组内的元素顺序
思路图:间示例1和2
源代码:

如果你要是去尝试这道题,那么必然会出现下面这种情况
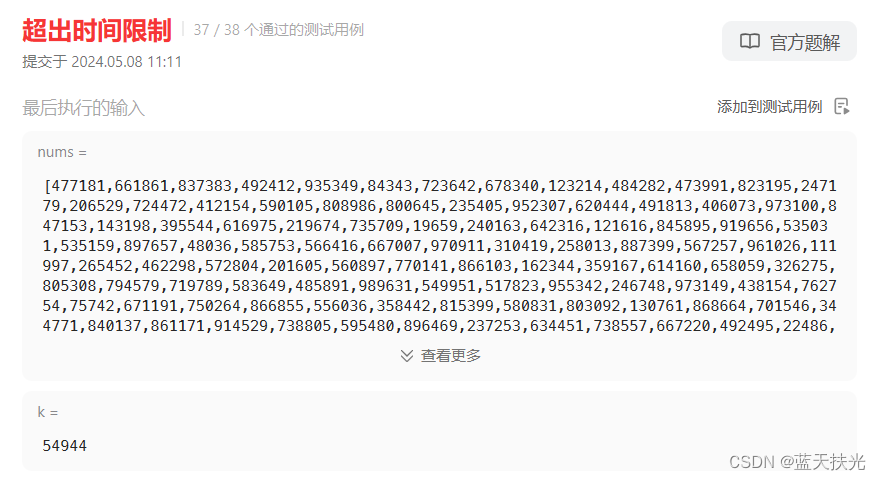
因此,我给大家讲一下思路二。
思路二:
我们还是先用位置个数k和元素个数取模,取好模后,将其分为两部分分别为位置k前和位置k后传给另一个函数(需要自己创建),通过循环将数组内的数字进行排序
思路图:

源代码:

文章重点总结
1.简单了解时间复杂度
2.大O阶法表示案例
3.时间复杂度的最好最坏以及平均情况
4.时间复杂度例题讲解
今天的内容就先到这啦,我们下次再见
给每一个努力的小伙伴点赞👍








![[论文笔记]Corrective Retrieval Augmented Generation](https://img-blog.csdnimg.cn/img_convert/3878170d5dcda1dfc9a8de7c8d867086.png)