文章目录
- 一、机器学习简介
- 1. 机器学习的相关定义
- 2. 一次简单的机器学习任务:鸢尾花分类
- 二、数据与数据集相关概念
- 1. 数据与数据集
- 2. 特征与标签
- 3. 连续变量和离散变量
- 4. 模型类型
- 三、机器学习建模一般流程
- 1. 提出基本模型
- 2. 确定损失函数
- 3. 根据损失函数性质,选择优化方法
- 4. 利用优化算法进行损失函数求解
一、机器学习简介
1. 机器学习的相关定义
- 一个计算机程序(算法),利用经验 E (历史数据)来学习任务 T (围绕某个问题进行训练),性能表现为 P (模型评估结果),如果针对任务 T 的性能 P 能随着经验 E 不断增长,则称之为机器学习。
- 对上述定义,我们有一个更加通俗易懂的解释,就是通过不断地喂养数据,让算法变得越来越聪明,就叫做机器学习。
- 机器学习算法指可以通过一次次的数据,不断累积经验,能够在既定任务处理上越来越聪明的计算流程。机器学习用到的算法也被称为机器学习算法、机器学习模型等。
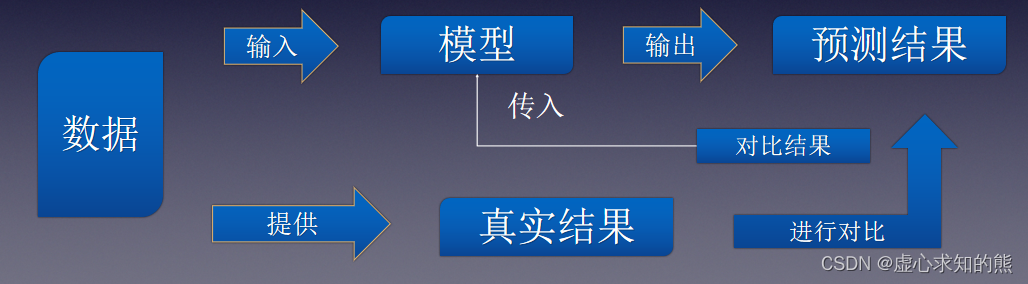
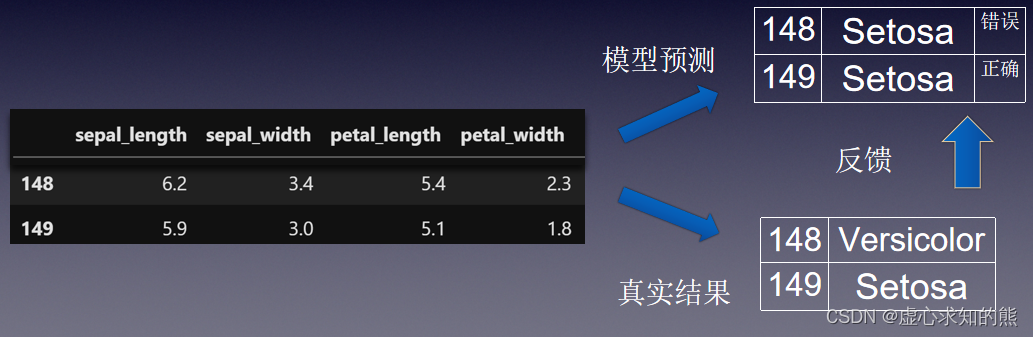
- 要想使机器学习算法变得越来越聪明,就需要进行反馈操作,输入新数据的预测结果判别是否正确。
- 模型评估是指模型输出之后,来自真实数据反馈的外在数值表现。
- 算法参数是指对模型运行及输出结果有所影响的模型关键指标(例如,算法规定的计算流程是两个数加权求和,则参数就是两个变量的权重。权重不同,模型最终输出结果也不同)。
- 模型训练是指根据模型输出结果的反馈结果,来不断调整模型参数,最终让模型性能提升的过程。其具体流程如下。
2. 一次简单的机器学习任务:鸢尾花分类

- (1) 获取历史数据,描述这朵花的基本信息和种类。
- (2) 将数据输入模型/算法,学习历史数据,判断满足什么条件时属于什么种类。
- (3) 新数据预测,在学习完成后,就可以在模型中输入新的数据,对其类型进行判断。
- (4) 反馈机制,对输入新数据的预测结果判别是否正确,使得整体计算流程越来越聪明。
二、数据与数据集相关概念
1. 数据与数据集
- 所谓数据,特指能够描绘某件事物的属性或者运行状态的数值,并且一个数据集由多条数据构成。
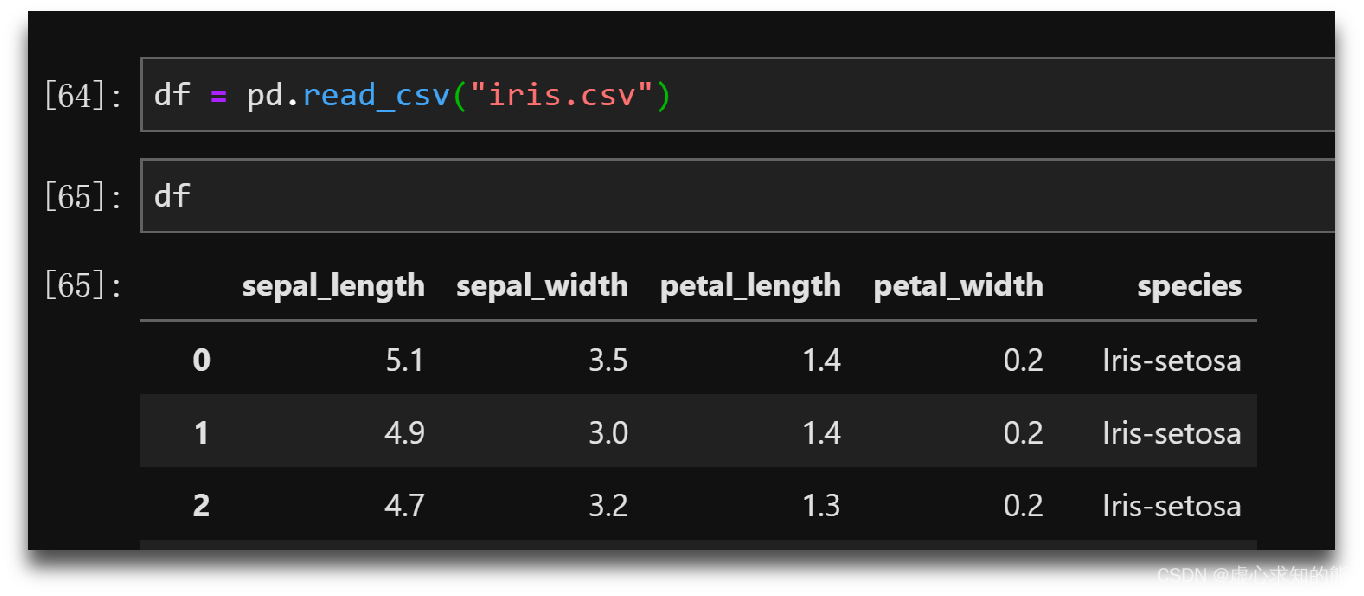
- 例如上文中的中鸢尾花数据,就是描述鸢尾花一般属性的数据集。我们可以通过本地读取文件的方式查看该数据集。
- 通过在 Jupyter Notebook 中输入如下代码即可。
import numpy as np
import pandas as pd
iris_df = pd.read_csv("E:\百度网盘\iris.csv")
iris_df
- 在其中填写文件的目录,大家一般情况下是通过属性当中的文件目录直接复制粘贴,但这样操作会报错 OSError: [Errno 22] Invalid argument: ‘\u202aD‘ ,对于此处的解决办法有两种。
- (1) 鼠标在路径前端,点击一次删除后再次运行。
- (2) 将文件的路径先复制好,再手动输入或重命名复制文件名,再次运行。
- 会将 iris.csv 中的数据读取出来(包括 150 行,5 列,以及对应的标签),具体运行结果如下所示。
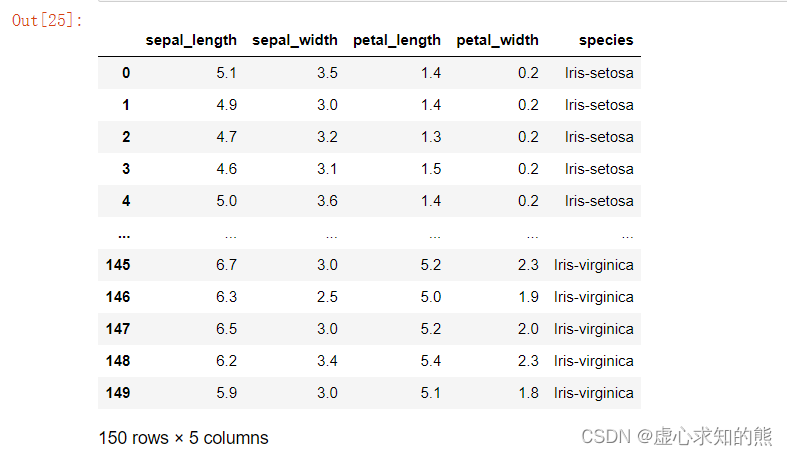

- 在上述数据集中,每一行代表一朵花的记录结果,而其中每一列代表所有花的一项共同指标。
- 类似这种二维表格数据,有时也被称为面板数据,属于结构化数据的一种。
2. 特征与标签
- 鸢尾花数据集中的每一列是所有描述对象的一项共同指标,其中,前四列分别描述了鸢尾花的四项生物学性状,而最后一列则描述了每一朵花所属类别。
- 当然,如果上述表格的记录目的是通过记录鸢尾花的四个维度的不同属性的取值最终判别鸢尾花属于哪一类,则该数据集中的前四列也被称为数据集的特征(features),而最后一列被称为数据集的标签(labels)。
- 据此,我们在实际建模过程中,当需要利用模型进行预测时时,也是通过输入模型一些样本的特征(一些鸢尾花的四个特征取值),让模型进行每个样本的标签判别(判别每一朵花应该属于哪一类)。
- 标签和特征,只是依据模型预测目标进行的、围绕数据集不同列进行的划分方式,如果模型的预测目标发生变化,则数据集的特征和标签也会发生变化。
- 例如,如果围绕鸢尾花数据集我们最终是进行每一朵花的花瓣宽(petal width)的预测,则上述数据集中1、2、3、5列就变成了特征,第4列变成了标签。因此,特征和标签本质上都是人工设置的。
- 一般来说,标签列需要放在最后一列,以便于我们的观察对比。
- 数据集中的列也被称为字段,鸢尾花数据集中总共有5列,也就总共有5个字段。
3. 连续变量和离散变量
- 对于鸢尾花数据而言,由于每一条数据都记录了一朵花的四个维度的属性以及花的所属类别,因此,如果从随机变量的角度出发,每一组观测结果我们也能将其视作5个随机变量的一次观测值。
- 例如,我们可以将花萼长(sepal length)看成是一个随机变量,而第一条数据中的5.1cm,则可看成这个随机变量的第一个观测值。
- 随机变量有离散变量和连续变量之分。
- 连续变量,指的是随机变量能够取得连续数值,例如随机变量表示距离或者长度测算结果时,该变量就是连续性变量。
- 离散变量,指的是随机变量只允许取得离散的整数,例如随机变量用 0/1 表示性别。不难发现,鸢尾花数据集中前四个变量都是连续变量,而最后一个变量是离散型变量(或者说可以用离散变量表示)。
- 也就是说鸢尾花数据集的特征都是连续型特征,而标签则是离散型标签。
- 知识点补充:对于离散型变量,可以细分为名义型变量和顺序性变量。
- 名义变量,指的是随机变量取得不同离散值时,取值大小本身没有数值意义,只有指代意义。例如,用 0/1 代表男女,则该变量没有 1>0 的数值意义。但
- 顺序变量,则有大小方面的数值意义,例如使用 0/1/2 代表高中/本科/研究生学历,则可用 2>1>0 来表示学习的高低之分。
4. 模型类型
- 离散型变量和连续性变量在数理特征上有很大的区别。因此,对于预测类的机器学习建模来说,标签这一预测指标是连续型变量还是离散型变量,会对模型预测过程造成很大影响。
- 如果是围绕离散型标签进行建模预测,则称任务为分类预测任务,该模型为解决分类任务的分类(classification)模型,
- 如果是围绕连续型标签进行建模预测,则称该任务为回归预测任务,该模型为解决回归问题的回归类(regression)模型。
- 如果依据鸢尾花数据集来构建一个预测某一朵花属于哪个类型的任务,属于分类任务,对应的,若需要完成该任务,我们也需要构建对应的分类模型来进行预测。此外,我们再介绍另外一个用于回归类问题建模的数据集,abalone 数据集。
- 由于 abalone 数据集是 txt 格式数据集,各列是通过空格进行分隔,并且第一行没有列名,因此我们需要使用下述语句进行读取(“ sep=‘\t’ 默认是由 tab 分割的数据,header=None 表示第一行就是数据)。
ab_df = pd.read_csv("E://百度网盘//abalone.txt", sep='\t', header=None)
ab_df
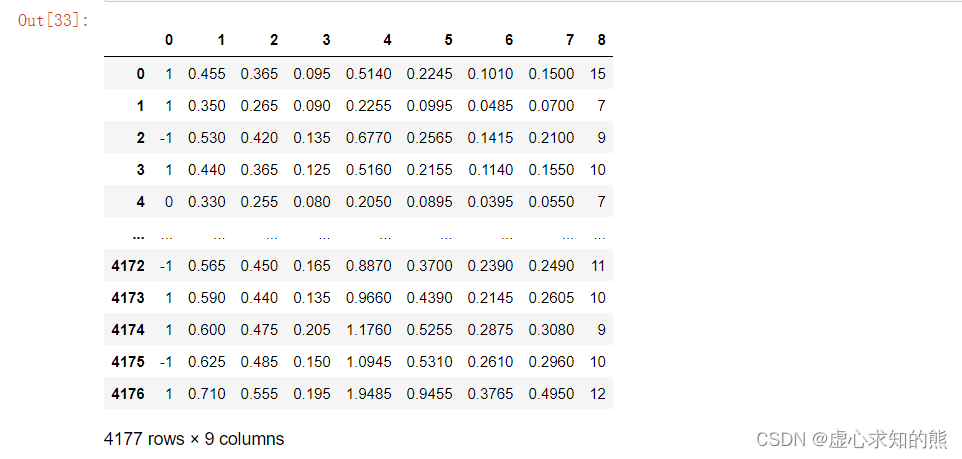
- 为了使阅读数据集更加方便,因此我们修改数据集列名称,并查看修改结果。
ab_df.columns
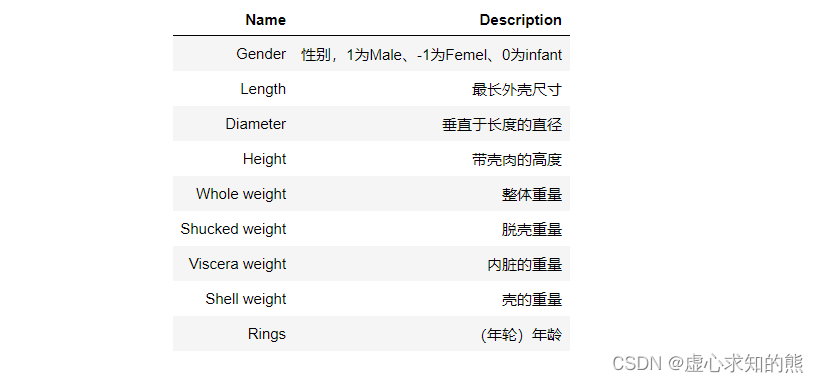
ab_df.columns = ['Gender', 'Length',
'Diameter', 'Height',
'Whole weight', 'Shucked weight',
'Viscera weight', 'Shell weight',
'Rings']
ab_df
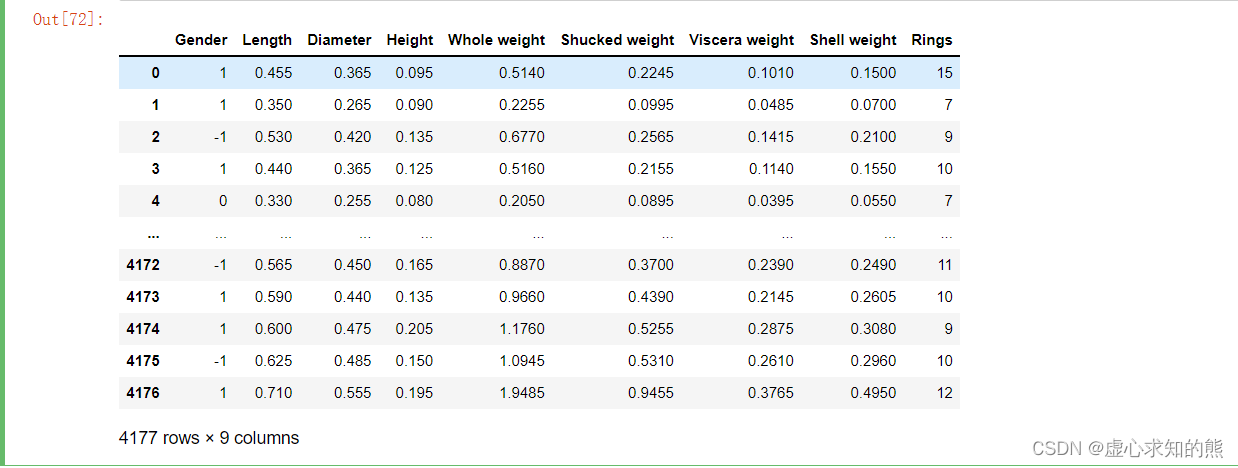
- 对于 abalone 数据集来说,Rings 是标签,围绕 Rings 的预测任务是连续型变量的预测任务,因此是个回归类问题。
三、机器学习建模一般流程
1. 提出基本模型
- 例如,利用简单线性回归去捕捉一个简单数据集中的基本数据规律。
- 例如 y=wx+b 就是我们所提出的基本模型。在提出模型时,我们往往会预设好一些影响模型结构或者实际判别性能的参数,如简单线性回归中的 w 和 b 。
2. 确定损失函数
- 围绕建模的目标构建评估指标,并且围绕评估指标设置损失函数。这里需要注意的是,损失函数不是模型,而是模型参数所组成的一个函数。
3. 根据损失函数性质,选择优化方法
- 损失函数既承载了我们优化的目标(让预测值和真实值尽可能接近),同时也是包含了模型参数的函数,当我们围绕目标函数求解最小值时,也就完成了模型参数的求解。
- 这个过程本质上就是一个数学的最优化过程,求解目标函数最小值本质上也就是一个最优化问题,而要解决这个问题,我们就需要灵活适用一些最优化方法。
- 在具体的最优化方法的选择上,函数本身的性质是重要影响因素,也就是说,不同类型、不同性质的函数会影响优化方法的选择。
- 在简单线性回归中,由于目标函数是凸函数,我们根据凸函数性质,我们选取了最小二乘法作为该损失函数的优化算法。
- 但实际上,简单线性回归的损失函数其实是所有机器学习模型中最简单的一类损失函数。
4. 利用优化算法进行损失函数求解
- 在确定优化方法之后,我们就能够借助优化方法对损失函数进行求解,当然在大多数情况下我们都是求解损失函数的最小值。
- 伴随损失函数最小值点确定,我们也就找到了一组对应的损失函数自变量的取值,而改组自变量的取值也就是模型的最佳参数。损失函数的求解过程才是建模的主体。