二叉树进阶 --- 中

news2024/11/17 3:28:56

目录

1. find 的递归实现

2. insert 的递归实现

3. erase 的递归实现

3.1. 被删除的节点右孩子为空

3.2. 被删除的节点左孩子为空

3.3. 被删除的节点左右孩子都不为空

4. 析构函数的实现

5. copy constructor的实现

6. 赋值运算符重载

7. 搜索二叉树的完整实现

1. find 的递归实现

find的递归实现较为简单，思路是：根据当前节点的 key 与传入的 key 作比较：

  • 如果前者大于后者，那么当前节点往左子树走；
  • 如果前者小于后者，那么当前节点往右子树走；
  • 如果两者相等，返回true；
  • 走到空，返回false。

代码实现：

// 对外提供的
bool find_recursion(const T& key)
{
	return _find_recursion(_root, key);
}
// 类中私有的
bool _find_recursion(Node* root, const T& key)
{
	if (root == nullptr)
		return false;
	else
	{
		if (root->_key < key)
			return _find_recursion(root->_right, key);
		else if (root->_key > key)
			return _find_recursion(root->_left, key);
		else
			return true;
	}
}

2. insert 的递归实现

insert分为两个过程

  • 第一个过程：找到合适位置；
  • 第二个过程：构建新节点，并完成连接关系。

假如现在我们已经得到了合适的插入位置，那么如何连接呢？

例如，如下图所示：我们要插入13这个数据，现在的关键问题是，如何将15和13这两个节点连接起来呢？ 具体如下：

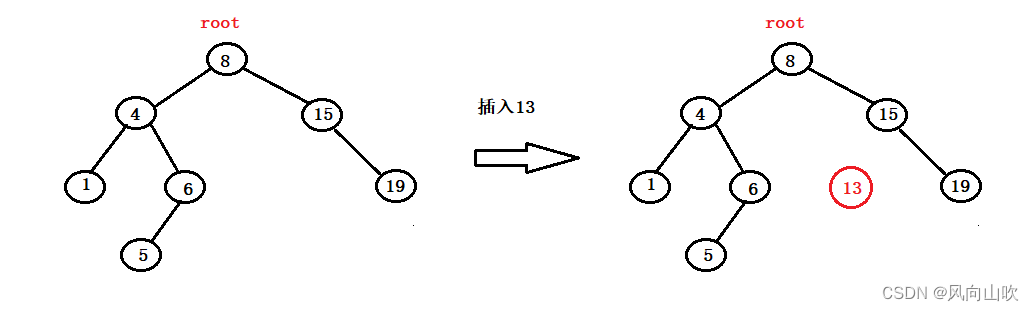
第一种方法：调用函数时，将父亲节点即这里的15也传进来。找到合适位置，创建节点并连接。

但是我们在这里提出一个较好玩的玩法，利用引用传参，如下所示：

// 对外提供的
bool insert_recursion(const T& key)
{    
	return _insert_recursion(_root, key);
}
// 类中私有的
bool _insert_recursion(Node*& root, const T& key)
{
	if (root == nullptr)
	{
		// 走到空, 说明找到了目标位置, 需要构建新节点, 并完成连接关系
        // 在这里, 我们用上图解释:
        // root就是15这个节点的左孩子的引用，即root就是15的左孩子
        // 给root new了一个node(key),等价于插入了这个节点,并连接了起来.
		root = new Node(key);
		return true;
	}
	else
	{
		if (root->_key < key)
			return _insert_recursion(root->_right, key);
		else if (root->_key > key)
			return _insert_recursion(root->_left, key);
		else
			return false;
	}
}

3. erase 的递归实现

对于erase的递归实现，其实也可以分为两个过程：

  • 第一个过程：找到这个要删除的特殊节点；
  • 第二个过程：可以分为三种情况(左孩子为空、右孩子为空、左右孩子都不为空)，根据不同情况进行删除。

假设我们现在已经得到了要删除节点的位置，该如何删除呢？

3.1. 被删除的节点右孩子为空

如图所示：我们要删除6号节点(其右孩子为空)，该如何删除：

 

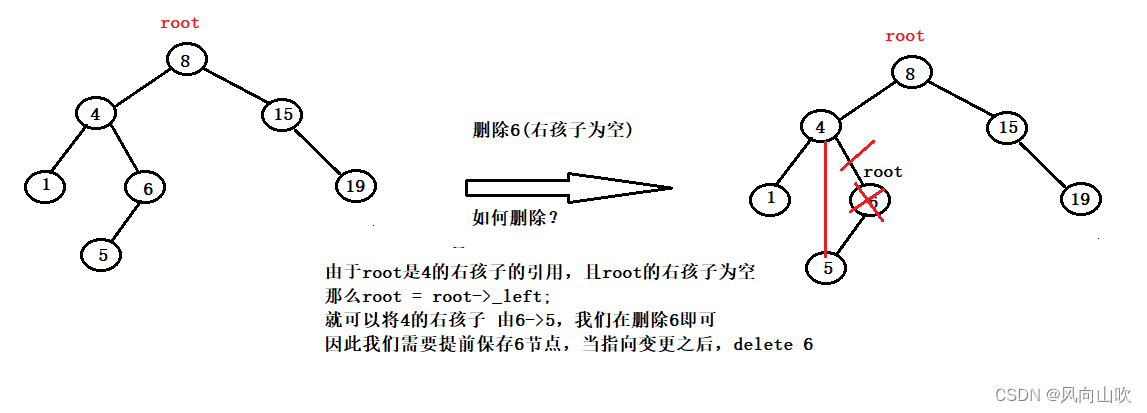
由于 root 是4的右孩子的引用，且 root 的右孩子为空，那么root = root->_left，就可以将4的右孩子由6变更为5，我们在删除6即可，因此我们需要提前保存6节点，当指向变更之后，delete 6。

3.2. 被删除的节点左孩子为空

如图所示：我们要删除15号节点(其左孩子为空)，该如何删除：

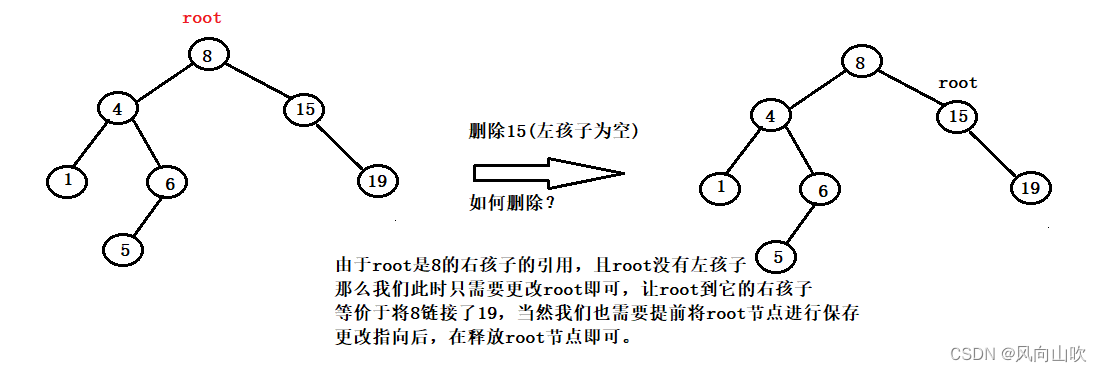
由于 root 是8的右孩子的引用，且 root 没有左孩子，那么我们此时只需要更改 root 即可，让 root 到它的右孩子 (root = root->_right)，等价于将8连接了19，当然我们也需要提前将 root 节点进行保存，更改指向后，在释放 root 节点即可。

3.3. 被删除的节点左右孩子都不为空

较为复杂的就是第三种情况了，由于此时被删除节点有两个孩子，因此无法像上面两种情况进行处理。此时我们还是要利用循环实现的思路：

  • (1)：从被删除的节点开始，先找到左子树的最大节点or右子树的最小节点(我在这里称之为"合适节点")；
  • (2)：交换这个"合适结点"和被删除节点的key；
  • (3)：将删除原节点转化为删除我们后找的这个"合适节点"。

在这里我们用实例说明，如下图所示：如果我要删除下图中的4，该如何删除？

我在这里实现的"合适节点"是： 左子树的最大(右)节点

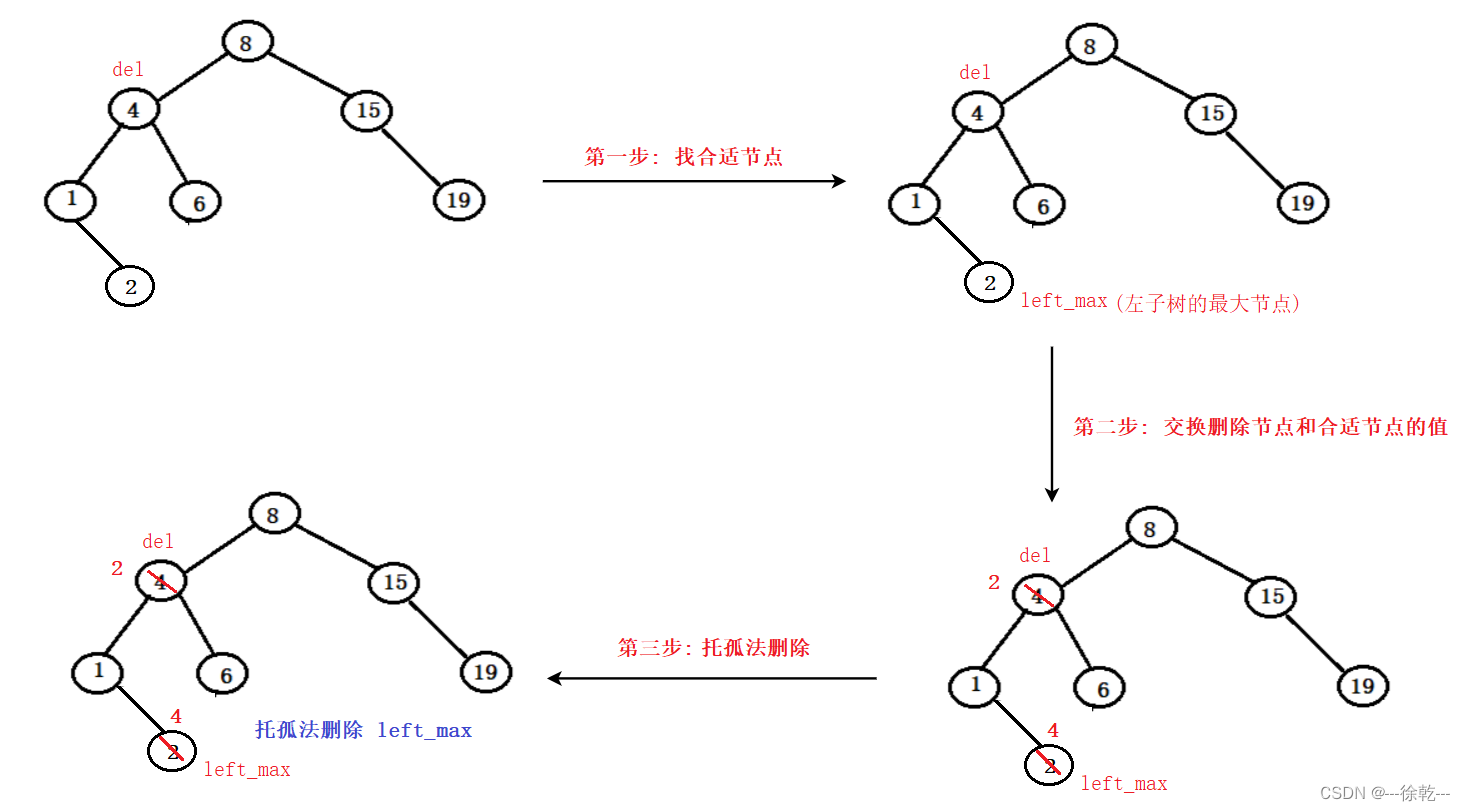
相信前两个过程是没有困难的，最后一步可能不好实现，但是当我们经过了前两个过程，我们发现被删除节点变成了我们找到的"合适节点"，而且这个"合适节点"很有特征，如果它是左子树的最大值，那么它一定不会有右子树，反之，如果他是右子树的最小节点，那么它一定不会有左子树。因此我们可以在递归一次，如果"合适节点"是左子树的最大节点，那么我们递归树的左子树即可，反之如果是右子树的最小节点，那么我们递归树的右子树即可。

代码如下：

// 对外提供的
bool erase_recursion(const T& key)
{
	return _erase_recursion(_root, key);
}
// 类中私有的
bool _erase_recursion(Node*& root, const T& key)
{
	if (!root)
		return false;
	else
	{
		// 如果当前节点的key > 目标key，那么递归它的左子树即可
		if (root->_key > key)
			return _erase_recursion(root->_left, key);
		// 如果当前节点的key < 目标key，那么递归它的右子树即可
		else if (root->_key < key)
			return _erase_recursion(root->_right, key);
		// 如果找到了,进行删除
		else
		{
			// 此时的root就是要删除的节点
			Node* del = root;
			// a. 左子树为空
			if (root->_left == nullptr)
				root = root->_right;
			// b. 右子树为空
			else if (root->_right == nullptr)
				root = root->_left;
			// c. 左右子树都不为空
			else
			{
				// 左子树的最右节点
				Node* left_max = root->_left;
				while (left_max->_right)
					left_max = left_max->_right;
				// 交换"合适节点"和"被删除节点"的key
				std::swap(left_max->_key, root->_key);
				// 在这里递归左子树即可
				return _erase_recursion(root->_left, key);
			}
			delete del;
			del = nullptr;
			return true;
		}
	}
}

4. 析构函数的实现

析构函数的实现我们依据的是后序的思想(LRN)，先析构左子树、然后是右子树、最后才是根。这种实现的原因是是少了许多的记录信息，例如在这里我们就不用记录下一个节点。因为我们释放的就是当前的叶子节点。

具体实现如下：

~BinarySearchTree()
{
	_BSTDestroy(_root);
}
// 注意我们这里传递的是根的引用
void _BSTDestroy(Node*& root)
{
	if (root == nullptr)
		return;
	else
	{
		// 依据后序的思想
		_BSTDestroy(root->_left);
		_BSTDestroy(root->_right);
		delete root;
		root = nullptr;
	}
}

5. copy constructor的实现

老生常谈的问题，如果我们没有显示实现拷贝构造函数，那么编译器默认生成的拷贝构造会对内置类型按照字节序的方式进行拷贝，对自定义类型成员属性会去调用它的拷贝构造函数。而字节序的方式进行拷贝会带来两个问题：

  • 其一，其中一个对象的修改会影响另一个对象；
  • 其二，同一空间会被析构两次，进程crash。

因此，我们在这里必须要实现深拷贝，那如何实现呢？我们可以借助前序的思想(NLR)。从根节点开始进行构造节点，然后递归构造它的左子树和右子树。注意构造的时候需要它们的连接关系。

代码如下：

BinarySearchTree(const BinarySearchTree<T>& copy)
{
	_root = _creat_new_root(copy._root);
}
Node* _creat_new_root(Node* root)
{
	// 如果遇到空了,就不用构造了
	if (root == nullptr)
		return nullptr;
	else
	{
		// 根据前序的思想(NLR),依次构造它的根、左子树、右子树   
		// 同时将它们连接起来
		Node* new_root = new Node(root->_key);
		new_root->_left = _creat_new_root(root->_left);
		new_root->_right = _creat_new_root(root->_right);
		return new_root;
	}
}

6. 赋值运算符重载

赋值运算符重载就比较简单了，因为我们已经实现了copy constructor，在这里利用传值传参会进行拷贝构造的特性实现我们的赋值

代码如下：

// 传值传参会进行拷贝构造
BinarySearchTree<T>& operator=(BinarySearchTree<T> copy)
{
	std::swap(_root, copy._root);
	return *this;
}

7. 搜索二叉树的完整实现

代码如下：

#ifndef _BINARY_SEARCH_TREE_HPP_
#define _BINARY_SEARCH_TREE_HPP_

#include <iostream>

namespace Xq
{

	template<class T>
	struct BinarySearchTreeNode
	{
		BinarySearchTreeNode<T>* _left;
		BinarySearchTreeNode<T>* _right;
		T _key;

		BinarySearchTreeNode(const T& key) :_key(key), _left(nullptr), _right(nullptr) {}
	};

	template<class T>
	class BinarySearchTree
	{
	private:
		typedef BinarySearchTreeNode<T> Node;
	public:
		BinarySearchTree(Node* root = nullptr) :_root(root) {}

		bool insert(const T& key)
		{
			// 1. 如果是空树,直接对_root赋值即可,插入成功并返回true
			if (_root == nullptr)
			{
				_root = new Node(key);
				return true;
			}
			else
			{
				// step 1: 先找目标位置
				Node* cur = _root;
				// 为了更好的连接新节点, 因此记录父节点
				Node* parent = nullptr;

				while (cur)
				{
					// 如果当前节点的Key大于目标Key
					// 当前节点应该向左子树走
					if (cur->_key > key)
					{
						parent = cur;
						cur = cur->_left;
					}
					// 如果当前节点的Key小于目标Key
					// 当前节点应该向右子树走
					else if (cur->_key < key)
					{
						parent = cur;
						cur = cur->_right;
					}
					else
					{
						// 找到了相同的 key, 在这里不插入
						return false;
					}
				}

				// cur 走到了空, 即 cur 就是合适的位置
				cur = new Node(key);
				// 我们需要判断cur是parent的左节点还是右节点
				// 如果key小于parent的key,那么插入左节点
				if (key < parent->_key)
					parent->_left = cur;
				// 反之连接到右节点
				else
					parent->_right = cur;
				return true;
			}
		}

		bool find(const T& key)
		{
			// 1. 从根节点开始
			Node* cur = _root;
			while (cur)
			{
				// 2. 如果当前关键字大于目标关键字,那么向左子树走
				if (cur->_key > key)
					cur = cur->_left;
				// 3. 如果小于目标关键字,那么向右子树走
				else if (cur->_key < key)
					cur = cur->_right;
				// 4. 相等，就返回true
				else
					return true;
			}
			// 5. 循环结束,说明没找到, 返回false
			return false;
		}

		bool erase(const T& key)
		{
			// 先找要删除的节点
			Node* del = _root;
			Node* del_parent = nullptr;

			while (del)
			{
				if (del->_key < key)
				{
					del_parent = del;
					del = del->_right;
				}
				else if (del->_key > key)
				{
					del_parent = del;
					del = del->_left;
				}
				else
				{
					// 锁定了要删除的节点
					// 分三种情况:
					// case 1: 左子树为空
					if (del->_left == nullptr)
					{
						// 如果要删除的节点是根
						if (del == _root)
						{
							Node* newroot = del->_right;
							delete _root;
							_root = newroot;
						}
						else
						{
							// 托孤法删除
							if (del_parent->_left == del)
								del_parent->_left = del->_right;
							else
								del_parent->_right = del->_right;
							delete del;
							del = nullptr;
						}
					}
					// case 2: 右子树为空
					else if (del->_right == nullptr)
					{
						if (_root == del)
						{
							Node* newroot = del->_left;
							delete _root;
							_root = newroot;
						}
						else
						{
							if (del_parent->_left == del)
								del_parent->_left = del->_left;
							else
								del_parent->_right = del->_left;
							delete del;
							del = nullptr;
						}
					}
					// case 3: 左右子树都不为空
					else
					{
						// 从被删除节点开始, 找右子树的最小(左)节点 || 找左子树的最大(右)节点
						if (del->_right)
							_erase_right_min_node(del);
						else
							_erase_left_max_node(del);
					}
					return true;
				}
			}

			return false;
		}

		bool find_recursion(const T& key)
		{
			return _find_recursion(_root, key);
		}

		bool insert_recursion(const T& key)
		{
			return _insert_recursion(_root, key);
		}

		bool erase_recursion(const T& key)
		{
			return _erase_recursion(_root, key);
		}

		~BinarySearchTree()
		{
			_BSTDestroy(_root);
		}

		BinarySearchTree(const BinarySearchTree<T>& copy)
		{
			_root = _creat_new_root(copy._root);
		}

		// 传值传参会进行拷贝构造
		BinarySearchTree<T>& operator=(BinarySearchTree<T> copy)
		{
			std::swap(_root, copy._root);
			return *this;
		}

		void InOrder()
		{
			_InOrder(_root);
			std::cout << std::endl;
		}

	private:
		void _InOrder(Node* root)
		{
			if (root)
			{
				_InOrder(root->_left);
				std::cout << root->_key << " ";
				_InOrder(root->_right);
			}

		}

		bool _find_recursion(Node* root, const T& key)
		{
			if (root == nullptr)
				return false;
			else
			{
				if (root->_key < key)
					return _find_recursion(root->_right, key);
				else if (root->_key > key)
					_find_recursion(root->_left, key);
				else
					return true;
			}
		}

		bool _insert_recursion(Node*& root, const T& key)
		{
			if (root == nullptr)
			{
				root = new Node(key);
				return true;
			}
			else
			{
				if (root->_key < key)
					return _insert_recursion(root->_right, key);
				else if (root->_key > key)
					return _insert_recursion(root->_left, key);
				else
					return false;
			}
		}

		void _erase_right_min_node(Node* del)
		{
			// 从被删除结点开始, 找右子树的最小(左)节点
			Node* right_min = del->_right;
			// 并记录这个节点的父亲节点, 让其从del开始
			Node* right_min_parent = del;
			while (right_min->_left)
			{
				right_min_parent = right_min;
				right_min = right_min->_left;
			}
			// 交换这个节点和要删除节点的 key
			std::swap(del->_key, right_min->_key);

			// 将删除 del 转化为删除 right_min (托孤法删除)
			if (right_min_parent->_left == right_min)
				right_min_parent->_left = right_min->_right;
			else
				right_min_parent->_right = right_min->_right;
			delete right_min;
			right_min = nullptr;
		}

		void _erase_left_max_node(Node* del)
		{
			// 从被删除节点开始, 找左子树的最大(右)节点
			Node* left_max = del->_left;
			// 并记录这个节点的父亲节点, 让其从del开始
			Node* left_max_parent = del;
			while (left_max->_right)
			{
				left_max_parent = left_max;
				left_max = left_max->_right;
			}
			// 交换这个节点和要删除节点的 key
			std::swap(del->_key, left_max->_key);

			// 将删除 del 转化为删除 left_max (托孤法删除)
			if (left_max_parent->_left == left_max)
				left_max_parent->_left = left_max->_left;
			else
				left_max_parent->_right = left_max->_left;
			delete left_max;
			left_max = nullptr;
		}

		bool _erase_recursion(Node*& root, const T& key)
		{
			if (!root)
				return false;
			else
			{
				// 如果当前节点的key > 目标key，那么递归它的左子树即可
				if (root->_key > key)
					return _erase_recursion(root->_left, key);
				// 如果当前节点的key < 目标key，那么递归它的右子树即可
				else if (root->_key < key)
					return _erase_recursion(root->_right, key);
				// 如果找到了,进行删除
				else
				{
					// 此时的root就是要删除的节点
					Node* del = root;
					// a. 左子树为空
					if (root->_left == nullptr)
						root = root->_right;
					// b. 右子树为空
					else if (root->_right == nullptr)
						root = root->_left;
					// c. 左右子树都不为空
					else
					{
						// 左子树的最右节点
						Node* left_max = root->_left;
						while (left_max->_right)
							left_max = left_max->_right;
						// 交换"合适节点"和"被删除节点"的key
						std::swap(left_max->_key, root->_key);
						// 在这里递归左子树即可
						return _erase_recursion(root->_left, key);
					}
					delete del;
					del = nullptr;
					return true;
				}
			}
		}

		Node* _creat_new_root(Node* root)
		{
			// 如果遇到空了,就不用构造了
			if (root == nullptr)
				return nullptr;
			else
			{
				// 根据前序的思想(NLR),依次构造它的根、左子树、右子树   
				// 同时将它们连接起来
				Node* new_root = new Node(root->_key);
				new_root->_left = _creat_new_root(root->_left);
				new_root->_right = _creat_new_root(root->_right);
				return new_root;
			}
		}

		// 注意我们这里传递的是根的引用
		void _BSTDestroy(Node*& root)
		{
			if (root == nullptr)
				return;
			else
			{
				// 依据后序的思想
				_BSTDestroy(root->_left);
				_BSTDestroy(root->_right);
				delete root;
				root = nullptr;
			}
		}

	private:
		Node* _root;
	};
}

#endif

二叉树进阶 --- 中，结束。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1665391.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

IM 是什么？

IM 是什么？

在当今数字化的时代&#xff0c;即时通讯&#xff08;IM&#xff09;已经渗透到人们的日常生活和企业的工作环境中。IM技术的快速i发展为人们提供了一种高效、便捷的沟通方式&#xff0c;不仅推动了社会的信息化进程&#xff0c;也提升了企业的协同效率和竞争力。 作为企业级I…
阅读更多...
API接口调用|京东API接口|淘宝API接口

API接口调用|京东API接口|淘宝API接口

什么是电商API接口&#xff1a; 电商API接口是电商服务平台对外提供的一种接口服务&#xff0c;允许第三方开发者通过编程方式与电商系统进行数据交互和功能调用。 这些接口提供了一种标准化的方法来获取、更新或处理电商平台上的商品信息、订单状态、用户数据、支付信息、物流…
阅读更多...
堆排序 之实现最小的K个数

堆排序 之实现最小的K个数

目录 1、方式一&#xff1a;通过自定义实现建堆和堆化操作 2、方式二&#xff1a;借助模块heapq实现 2.1、模块heapq的基本使用 2.2、使用heapq实现最小的k个数 3、堆在实际项目的应用 实现语言&#xff1a;Python 3.9 题目来源&#xff1a;牛客 分析&#xff1a; 要找…
阅读更多...
Offline: Overcoming Model Bias for Robust Offline Deep Reinforcement Learning

Offline: Overcoming Model Bias for Robust Offline Deep Reinforcement Learning

EAAI 2023 paper Intro model-free的离线强化学习由于价值函数估计问题存在训练的稳定性以及鲁棒性较低。本文提出基于模型的方法&#xff0c;同构构建稳定的动力学模型帮助策略的稳定训练。 method 本文基于模型的方法&#xff0c;所构造的转移模型输入状态动作&#xff0…
阅读更多...
500元以内的蓝牙耳机品牌怎么选？五大优质品牌汇总

500元以内的蓝牙耳机品牌怎么选？五大优质品牌汇总

无论是通勤途中、学习间隙还是运动时&#xff0c;一款性能出众、价格亲民的蓝牙耳机都能为我们带来极致的听觉享受&#xff0c;然而面对市场上琳琅满目的品牌和型号&#xff0c;如何选择一款500元以内的优质蓝牙耳机&#xff0c;相信大家都会有这个难题&#xff0c;今天为了帮助…
阅读更多...
去哪里找高清视频素材?推荐几个短视频素材免费网站

去哪里找高清视频素材?推荐几个短视频素材免费网站

在数字时代&#xff0c;视频内容的质量直接影响观众的吸引力和留存率。尤其是高清、4K视频素材和可商用素材&#xff0c;它们在提升视觉质量和叙事深度方面起到了至关重要的作用。以下是一些国内外的顶级视频素材网站&#xff0c;它们提供的资源将为您的创作提供极大的支持和灵…
阅读更多...
Java里的String使用

Java里的String使用

1.Java WinForm项目 public static void main(String[] args) {String testString"22";String testString2"1096";String testString3"22";Student studentnew Student();student.Age"22";Test(student.Age);Test2(student.Age); }pu…
阅读更多...
【吴恩达机器学习-week2】多个变量的特征缩放和学习率问题

【吴恩达机器学习-week2】多个变量的特征缩放和学习率问题

特征缩放和学习率&#xff08;多变量&#xff09; 目标 利用上一个实验中开发的多变量例程在具有多个特征的数据集上运行梯度下降探索学习率对梯度下降的影响通过 Z 分数归一化进行特征缩放&#xff0c;提高梯度下降的性能 import numpy as np np.set_printoptions(precisio…
阅读更多...
Appwrite 1.5 已在云端发布 - 四月产品更新

Appwrite 1.5 已在云端发布 - 四月产品更新

Hello, Appwriters&#x1f44b; 以下是四月份的产品更新和一个令人兴奋的消息&#xff1a; Appwrite 1.5 已在 Appwrite Cloud 上发布。这个版本备受期待&#xff0c;我们很高兴终于能与大家分享这个好消息。 为了让您快速复习&#xff0c;您现在可以开始使用云计算平台上的…
阅读更多...
视频资源汇聚平台常见的几种接入方式

视频资源汇聚平台常见的几种接入方式

视频资源汇聚平台 视频汇聚平台可以实现海量资源的接入、汇聚、存储、处理、分析、运维等&#xff0c;平台具备轻量化接入能力&#xff0c;可支持多协议方式接入&#xff0c;包括主流标准协议GB28181、RTSP、ONVIF、RTMP、FLV、WEBSOCKET等&#xff0c;以及厂家私有协议与SDK接…
阅读更多...
人脸识别之bbox【det_10g】-ncnn(c++)

人脸识别之bbox【det_10g】-ncnn(c++)

模型描述 det_10g是insightface 人脸框图和人脸关键点的分类&#xff0c;最终能够得到人脸框图bbox&#xff0c;分值还有人脸五官&#xff08;眼x2、鼻子x1、嘴巴x2&#xff09; 由于我这里没有采用最终结果&#xff0c;通过onnx转换为ncnn&#xff0c;所以后面的步骤结果丢弃…
阅读更多...
桌面怎么分类便签 桌面分类便签设置方法

桌面怎么分类便签 桌面分类便签设置方法

桌面便签&#xff0c;一直是我工作和学习的好帮手。每当灵感闪现或是有待办事项&#xff0c;我都会随手记录在便签上&#xff0c;它们就像我桌面上的小助手&#xff0c;时刻提醒我不要遗漏任何重要事务。 但便签一多&#xff0c;管理就成了问题。一张张五颜六色的便签贴满了我…
阅读更多...
autolabor(ROS开发笔记)__1

autolabor(ROS开发笔记)__1

视频链接&#xff1a;ROS机器人 chapter 1 ROS概述与环境搭建 学习步骤&#xff1a; 1.了解该模块的相关概念 是什么&#xff0c;为什么学&#xff0c;前世今生&#xff0c;发展前景 2.安装官方软件包 具备基本的开发环境&#xff0c;简陋notepad 3.搭建集成开发环境(IDE,Int…
阅读更多...
信息检索（35）：LEXMAE: LEXICON-BOTTLENECKED PRETRAINING FOR LARGE-SCALE RETRIEVAL

信息检索（35）：LEXMAE: LEXICON-BOTTLENECKED PRETRAINING FOR LARGE-SCALE RETRIEVAL

LEXMAE: LEXICON-BOTTLENECKED PRETRAINING FOR LARGE-SCALE RETRIEVAL 标题摘要1 引言2 相关工作3 LEXMAE&#xff1a;词典瓶颈屏蔽自动编码器3.1 语言建模编码器3.2 词典瓶颈模块3.3 弱化掩蔽式解码器3.4 词汇加权检索器的预训练目标和微调 4 实验4.1 主要评估4.2 效率分析与…
阅读更多...
[算法][单调栈] [leetcode]316. 去除重复字母

[算法][单调栈] [leetcode]316. 去除重复字母

去除重复字母 给你一个字符串 s &#xff0c;请你去除字符串中重复的字母&#xff0c;使得每个字母只出现一次。需保证 返回结果的 字典序最小&#xff08;要求不能打乱其他字符的相对位置&#xff09;。 字典序最小&#xff1a; 考虑字符串 a 与 字符串 b&#xff0c;如果字…
阅读更多...
JavaWeb：VsCode创建Web项目

JavaWeb：VsCode创建Web项目

一、Tomcat 先在官网上下载tomcat&#xff0c;解压到自己设定的文件夹。 配置环境变量 path变量配置 系统变量配置 验证服务器开机 二、Maven Maven 是一个基于 Java 的项目管理工具&#xff0c;可以对 Java 项目进行构建、依赖管理&#xff0c;可以自动下载所需要的包&#x…
阅读更多...
关于各类软件下载及使用

关于各类软件下载及使用

文章目录 一、VS Code1、下载2、安装3、使用 二、Dev-C1、下载2、安装3、使用 三、VS20191、下载2、安装3、使用 四、IDEA1、下载2、安装3、使用 五、Fiddler1、下载1.1 官网下载1.2 文件下载 2、安装3、使用 一、VS Code 1、下载 2、安装 3、使用 二、Dev-C 1、下载 2、…
阅读更多...
【蚂蚁笔试题汇总】2024-05-11-蚂蚁春招笔试题-三语言题解(CPP/Python/Java)

【蚂蚁笔试题汇总】2024-05-11-蚂蚁春招笔试题-三语言题解(CPP/Python/Java)

&#x1f36d; 大家好这里是清隆学长 &#xff0c;一枚热爱算法的程序员 ✨ 本系列打算持续跟新蚂蚁近期的春秋招笔试题汇总&#xff5e; &#x1f4bb; ACM银牌&#x1f948;| 多次AK大厂笔试 &#xff5c; 编程一对一辅导 &#x1f44f; 感谢大家的订阅➕ 和 喜欢&#x1f49…
阅读更多...
《超越代码生成：Agentic Reasoning探索研发智能化》——【研发效能·创享大会】

《超越代码生成：Agentic Reasoning探索研发智能化》——【研发效能·创享大会】

【研发效能创享大会】是由IDCF社区独家举办&#xff0c;这个会议主要聚焦于技术和研发管理&#xff0c;旨在为社区成员提供一个学习与交流的平台&#xff0c;分享技术经验&#xff0c;交流行业见解&#xff0c;促进技术合作与创新&#xff0c;发现并培养人才&#xff0c;推动软…
阅读更多...
新能源汽车动力电池浸没式冷却方案介绍与未来趋势

新能源汽车动力电池浸没式冷却方案介绍与未来趋势

前言 新能源汽车的兴起标志着汽车工业的一次革命&#xff0c;其中动力电池的设计与性能成为了关键。浸没式冷却方案作为一种新兴的技术&#xff0c;为动力电池系统提供了有效的散热解决方案&#xff0c;其在未来的发展趋势备受关注。 一 动力电池浸没式冷却方案介绍 首先&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023