文章目录
- 简介
- 基础知识
- 什么是Attention
- Self Attention
- 原理
- 通俗易懂理解
- 矩阵计算
- Q,K,V计算
- Self-Attention 的输出
- 优势
- Multi-head self-attention
- 原理
- 通俗易懂理解
- 矩阵计算
- 代码实现
简介
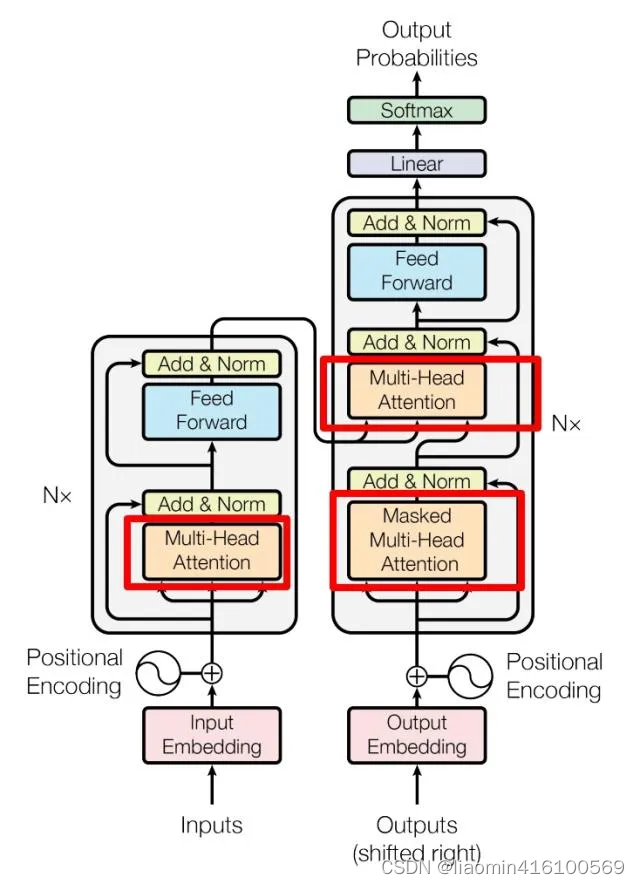
下图是论文中 Transformer 的内部结构图,左侧为 Encoder block,右侧为 Decoder block。红色圈中的部分为 Multi-Head Attention,是由多个 Self-Attention组成的,可以看到 Encoder block 包含一个 Multi-Head Attention,而 Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)。Multi-Head Attention 上方还包括一个 Add & Norm 层,Add 表示残差连接 (Residual Connection) 用于防止网络退化,Norm 表示 Layer Normalization,用于对每一层的激活值进行归一化。
因为 Self-Attention是 Transformer 的重点,所以我们重点关注 Multi-Head Attention 以及 Self-Attention,首先详细了解一下 Self-Attention 的内部逻辑。
基础知识
向量的内积是什么,如何计算,最重要的,其几何意义是什么?
内积的计算方法是将两个向量对应分量相乘,然后将结果相加。
内积的几何意义是非常重要的。在二维空间中,两个向量的内积等于两个向量的模(长度)之积乘以它们之间的夹角的余弦值。具体来说,如果
θ 是两个向量之间的夹角,则它们的内积为:
a
⋅
b
=
∣
a
∣
∣
b
∣
cos
(
θ
)
\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos(\theta)
a⋅b=∣a∣∣b∣cos(θ)
这个公式表明,内积可以用来衡量两个向量的相似程度。当两个向量的夹角为 0时(cos0=1),它们的内积取得最大值,表示它们的方向相同;当夹角为 90时(cos90=0),内积为 0,表示它们的方向垂直;当夹角为180(cos180=-1) 时,内积取得最小值,表示它们的方向相反。
一个矩阵 与其自身的转置相乘,得到的结果有什么意义?
矩阵的对称性指的是矩阵在某种变换下保持不变的性质。对称矩阵是一种特殊的矩阵,它满足以下性质:矩阵的转置等于它自身。
具体来说,对称矩阵 A 满足以下条件:
A
=
A
⊺
\mathbf{A} = \mathbf{A}^\intercal
A=A⊺
这意味着矩阵的主对角线上的元素保持不变,而其他元素关于主对角线对称。
例如,如果一个矩阵 A 的元素为:
A
=
(
a
b
c
b
d
e
c
e
f
)
\mathbf{A} = \begin{pmatrix} a & b & c \\ b & d & e \\ c & e & f \end{pmatrix}
A=
abcbdecef
矩阵中的元素对称于主对角线。
对称矩阵在数学和工程领域中非常重要,因为它们具有许多有用的性质,比如特征值都是实数、可以通过正交变换对角化等。在应用中,对称矩阵广泛用于描述对称系统、表示物理现象等。
当一个矩阵与其自身的转置相乘时,得到的结果矩阵具有重要的性质,其中最显著的是结果矩阵是一个对称矩阵。这个性质在许多领域中都有重要的应用,比如在统计学中用于协方差矩阵的计算,以及在机器学习中用于特征提取和数据降维。
让我们用一个具体的矩阵示例来演示这个性质。考虑一个
3
×
2
3 \times 2
3×2的矩阵
的矩阵
A
\mathbf{A}
A:
A
=
(
1
2
3
4
5
6
)
\mathbf{A} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix}
A=
135246
首先,我们计算 A 的转置
A
⊺
\mathbf{A}^\intercal
A⊺
A
⊺
=
(
1
3
5
2
4
6
)
\mathbf{A}^\intercal = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix}
A⊺=(123456)
然后,我们将 𝐴 相乘
A
⊺
\mathbf{A}^\intercal
A⊺,得到结果矩阵
A
A
⊺
\mathbf{A} \mathbf{A}^\intercal
AA⊺
A
A
⊺
=
(
1
2
3
4
5
6
)
(
1
3
5
2
4
6
)
=
(
5
11
17
11
25
39
17
39
61
)
\mathbf{A} \mathbf{A}^\intercal = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 11 & 17 \\ 11 & 25 & 39 \\ 17 & 39 & 61 \end{pmatrix}
AA⊺=
135246
(123456)=
51117112539173961
可以观察到,结果矩阵 A A ⊺ \mathbf{A} \mathbf{A}^\intercal AA⊺是一个对称矩阵。
什么是Attention
所谓Attention,顾名思义:注意力,意思是处理一个问题的时候把"注意力"放到重要的地方上。Attention思想其实是从人类的习惯中提取出来的。人们在第一次看一张照片的时候,第一眼一定落到这张照片的某个位置上,可能是个显著的建筑物,或者是一个有特点的人等等,总之,人们通常并没有看清图片的全部内容,而是将注意力集中在了图片的焦点上。
2017年的某一天,Google 机器翻译团队发表了《Attention is All You Need》这篇论文,犹如一道惊雷,Attention横空出世了!(有一说一,这标题也太他喵嚣张了,不过人家有这个资本(o゚▽゚)o )
Attention 机制最早是在计算机视觉里应用的,随后在NLP领域也开始应用了,真正发扬光大是在NLP领域,由于2018年GPT模型的效果显著,Transformer和Attention这些核心才开始被大家重点关注。
下面举个例子上说明一下注意力和自注意力,可能不够严谨,但足以说明注意力和自注意力是什么了。
首先我们不去考虑得到注意力分数的细节,而是把这个操作认为是一个封装好的函数。比如定义为attention_score(a,b),表示词a和b的注意力分数。现在有两个句子A=“you are beautiful”和B=“你很漂亮”,我们想让B句子中的词“你”更加关注A句子中的词“you”,该怎么做呢?答案是对于每一个A句子中的词,计算一下它与“you”的注意力分数。也就是把
attention_score(“you”,“你”)
attention_score(“are”,“你”)
attention_score(“beautiful”,“你”)
都计算一遍,在实现attention_score这个函数的时候,底层的运算会让相似度比较大的两个词分数更高,因此attention_score(“you”,“你”)的分数最高,也相当于告诉了计算机,在对B句子中“你”进行某些操作的时候,你应该更加关注A句子中的“you”,而不是“are”或者“beautiful”。
以上这种方式就是注意力机制,两个不同的句子去进行注意力的计算。而当句子只有一个的时候,只能去计算自己与自己的注意力,这种方式就是自注意力机制。比如只看A句子,去计算
attention_score(“you”,“you”)
attention_score(“are”,“you”)
attention_score(“beautiful”,“you”)
这种方式可以把注意力放在句子内部各个单词之间的联系,非常适合寻找一个句子内部的语义关系。
再举个例子比如这句话“这只蝴蝶真漂亮,停在花朵上,我很喜欢它”,我们怎么知道这个“它”指的是“蝴蝶”还是“花朵”呢?答案是用自注意力机制计算出这个“它”和其他所有输入词的“分数”,这个“分数”一定程度上决定了其他单词与这个联系。可以理解成越相似的,分就越高(通过权重来控制)。通过计算,发现对于“它”这个字,“蝴蝶”比“花朵”打的分高。所以对于“它”来说,“蝴蝶”更重要,我们可以认为这个“它”指的就是蝴蝶。
Self Attention
原理
通俗易懂理解
在人类的理解中,对待问题是有明显的侧重。具体举个例子来说:“我喜欢踢足球,更喜欢打篮球。”,对于人类来说,显然知道这个人更喜欢打篮球。但对于深度学习来说,在不知道”更“这个字的含义前,是没办法知道这个结果的。所以在训练模型的时候,我们会加大“更”字的权重,让它在句子中的重要性获得更大的占比。比如:
C
(
s
e
q
)
=
F
(
0.1
∗
d
(
我
)
,
0.1
∗
d
(
喜
)
,
.
.
.
,
0.8
∗
d
(
更
)
,
0.2
∗
d
(
喜
)
,
.
.
.
)
C(seq) = F(0.1*d(我),0.1*d(喜),...,0.8*d(更),0.2*d(喜),...)
C(seq)=F(0.1∗d(我),0.1∗d(喜),...,0.8∗d(更),0.2∗d(喜),...)
在知道了attention在机器学习中的含义之后(下文都称之为注意力机制)。人为设计的注意力机制,是非常主观的,而且没有一个准则来评定,这个权重设置为多少才好。所以,如何让模型自己对变量的权重进行自赋值成了一个问题,这个权重自赋值的过程也就是self-attention。
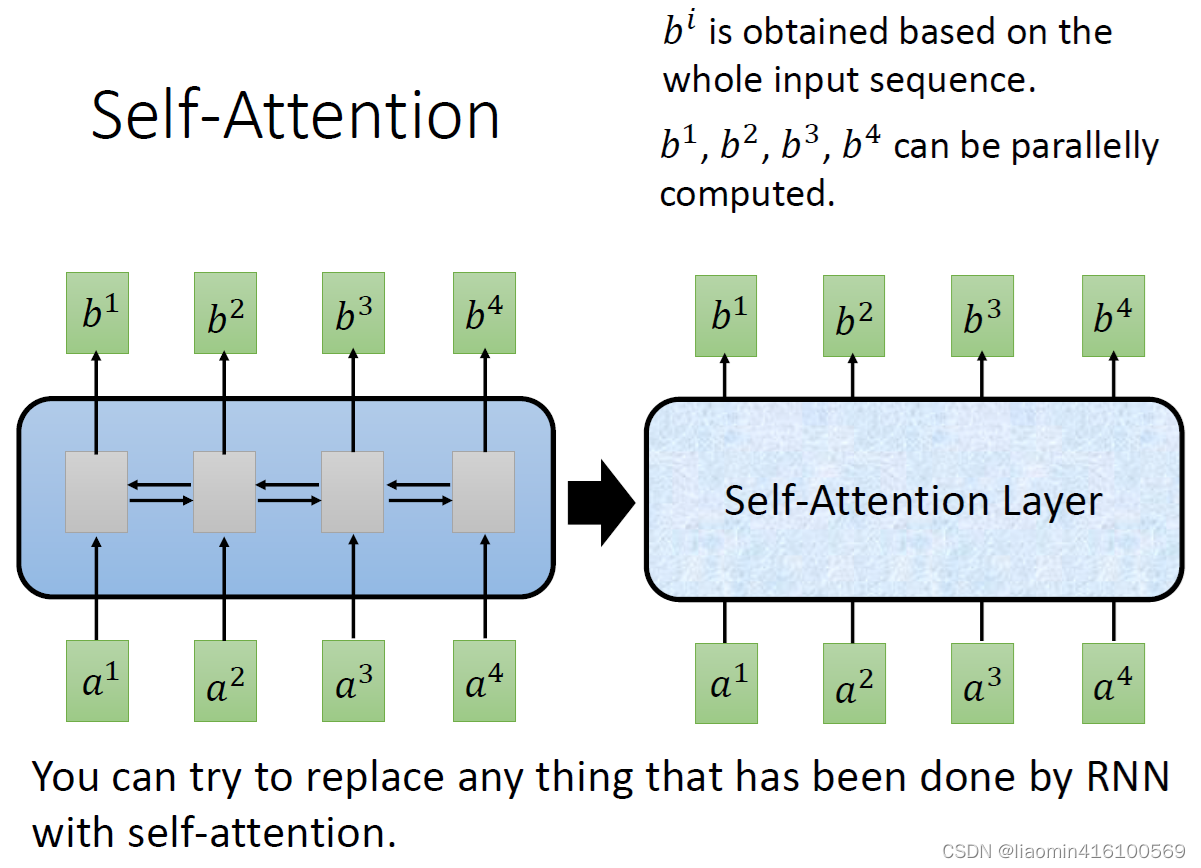
定义:假设有四个输入变量
a
1
a^1
a1,
a
2
a^2
a2,
a
3
a^3
a3,
a
4
a^4
a4,希望它们经过一个self-attention layer之后变为
b
1
b^1
b1,
b
2
b^2
b2,
b
3
b^3
b3,
b
4
b^4
b4

拿
a
1
a^1
a1和
b
1
b^1
b1做例子,
b
1
b^1
b1这个结果是综合了
a
1
a^1
a1,
a
2
a^2
a2,
a
3
a^3
a3,
a
4
a^4
a4而得出来的一个结果。既然得到一个b 是要综合所有的a才行,那么最直接的做法就是
a
1
a^1
a1与
a
2
a^2
a2,
a
3
a^3
a3,
a
4
a^4
a4
都做一次运算,得到的结果就代表了这个变量的注意力系数。直接做乘法太暴力了,所以选择一个更柔和的方法:引入三个变量
W
q
W^q
Wq,
W
k
W^k
Wk,
W
v
W^v
Wv这三个变量与
a
1
a^1
a1相乘得到
q
1
q^1
q1,
k
1
k^1
k1,
v
1
v^1
v1
同样的方法对
a
2
a^2
a2,
a
3
a^3
a3,
a
4
a^4
a4都做一次,至于这里的q , k , v具体代表什么,下面就慢慢展开讲解。
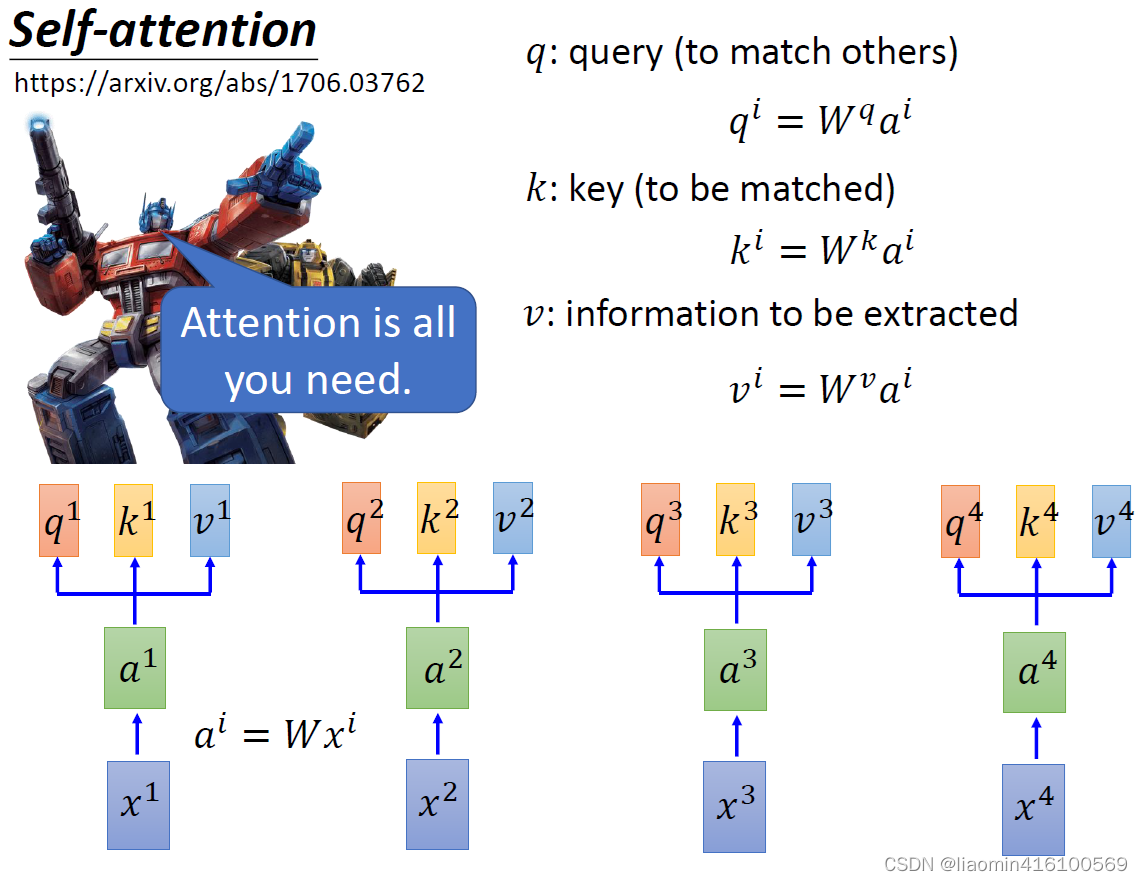
然后拿自己的q与别人的k相乘就可以得到一个系数
α
\alpha
α。这里
q
1
q^1
q1在和其他的k做内积时,可近似的看成是在做相似度计算(前面基础向量的内积)。比如:
α
1
,
1
=
q
1
⋅
k
1
α
1
,
2
=
q
1
⋅
k
2
α
1
,
3
=
q
1
⋅
k
3
α
1
,
4
=
q
1
⋅
k
4
\alpha_{1,1} =q^1\cdot k^1\\ \alpha_{1,2} =q^1\cdot k^2\\ \alpha_{1,3} =q^1\cdot k^3\\ \alpha_{1,4} =q^1\cdot k^4\\
α1,1=q1⋅k1α1,2=q1⋅k2α1,3=q1⋅k3α1,4=q1⋅k4
在实际的神经网络计算过程中,还得除于一个缩放系数
d
\sqrt{d}
d这个d是指q和k的维度,因为q和k会做内积,所以维度是一样的。之所以要除
d
\sqrt{d}
d,是因为做完内积之后,,
α
\alpha
α会随着它们的维度增大而增大,除
d
\sqrt{d}
d相当于标准化。
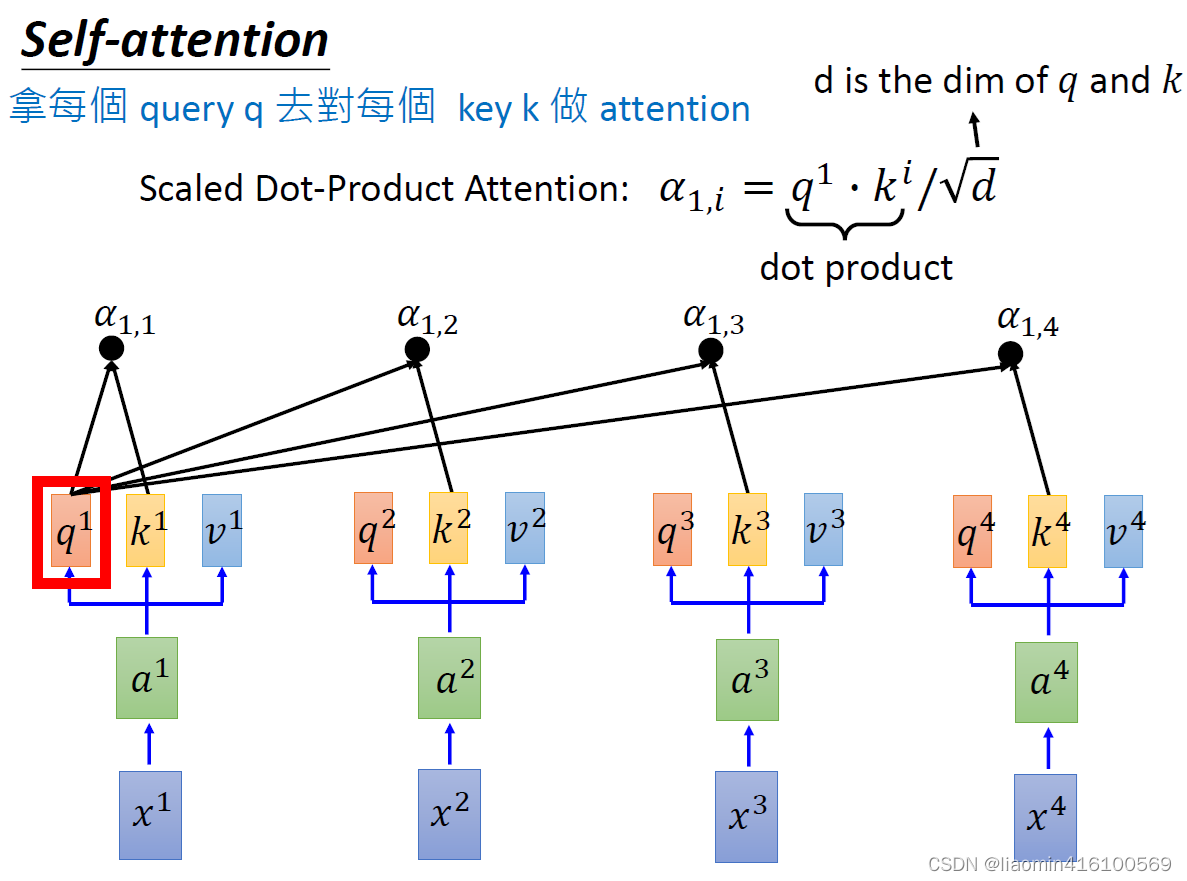
得到了四个
α
\alpha
α之后,我们分别对其进行softmax,得到四个
α
^
1
\hat{\alpha}_1
α^1,增加模型的非线性。
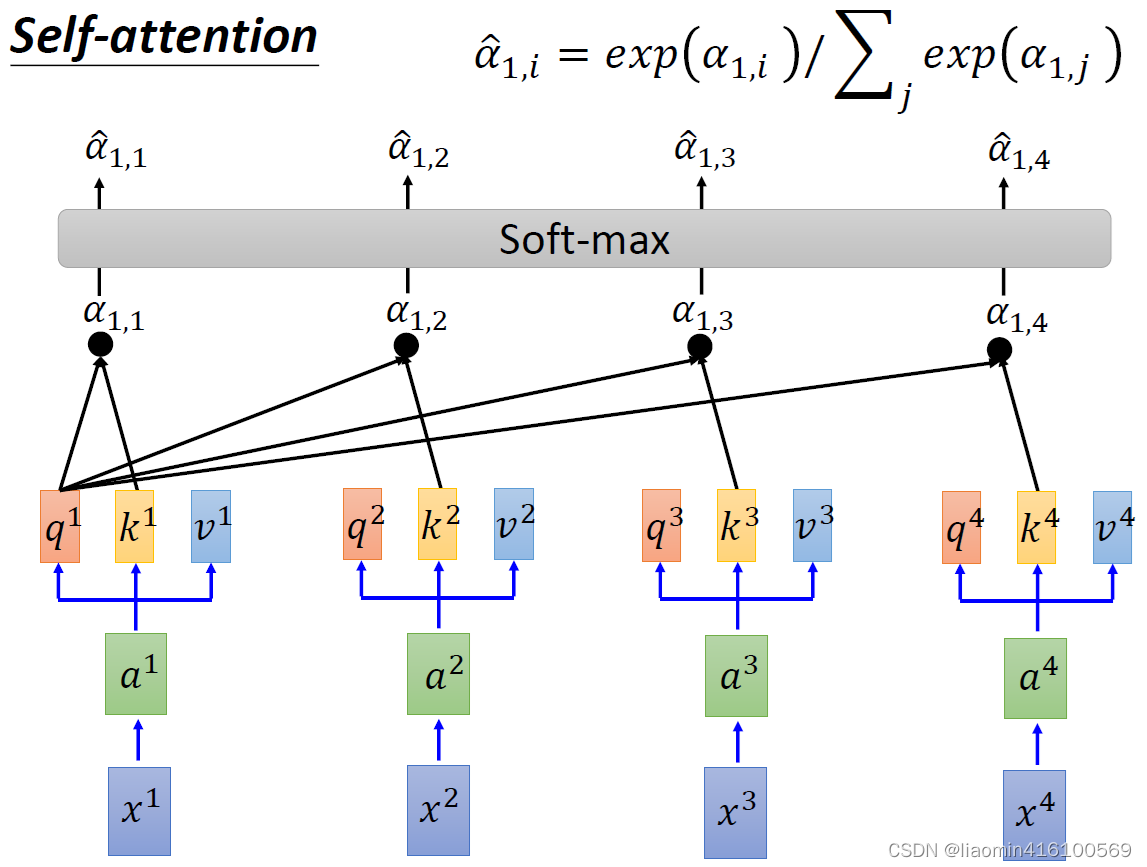
四个
α
\alpha
α分别是
α
^
1
\hat{\alpha}_1
α^1,
α
^
2
\hat{\alpha}_2
α^2,
α
^
3
\hat{\alpha}_3
α^3,
α
^
4
\hat{\alpha}_4
α^4,别忘了还有我们一开始计算出来的
v
1
{v}^1
v1,
v
2
{v}^2
v2,
v
3
{v}^3
v3,
v
4
{v}^4
v4,直接把各个
α
^
1
\hat{\alpha}_1
α^1直接与各个a 相乘不就得出了最后的结果了吗?虽然这么说也没错,但为了增加网络深度,将a变成v也可以减少原始的a对最终注意力计算的影响。
那么距离最后计算出
b
1
b^1
b1只剩最后一步,我们将所有的
α
^
1
\hat{\alpha}_1
α^1
与所有的v分别相乘,然后求和,就得出
b
1
b^1
b1啦!具体计算如下:
b
1
=
α
^
1
,
1
∗
v
1
+
α
^
1
,
2
∗
v
2
+
α
^
1
,
3
∗
v
3
+
α
^
1
,
4
∗
v
4
b^1=\hat{\alpha}_{1,1}*v^1+\hat{\alpha}_{1,2}*v^2+\hat{\alpha}_{1,3}*v^3+\hat{\alpha}_{1,4}*v^4
b1=α^1,1∗v1+α^1,2∗v2+α^1,3∗v3+α^1,4∗v4
公式简化为:
b
1
=
∑
i
α
^
1
,
i
∗
v
i
b^1=\sum_i\hat{\alpha}_{1,i}*v^i
b1=i∑α^1,i∗vi
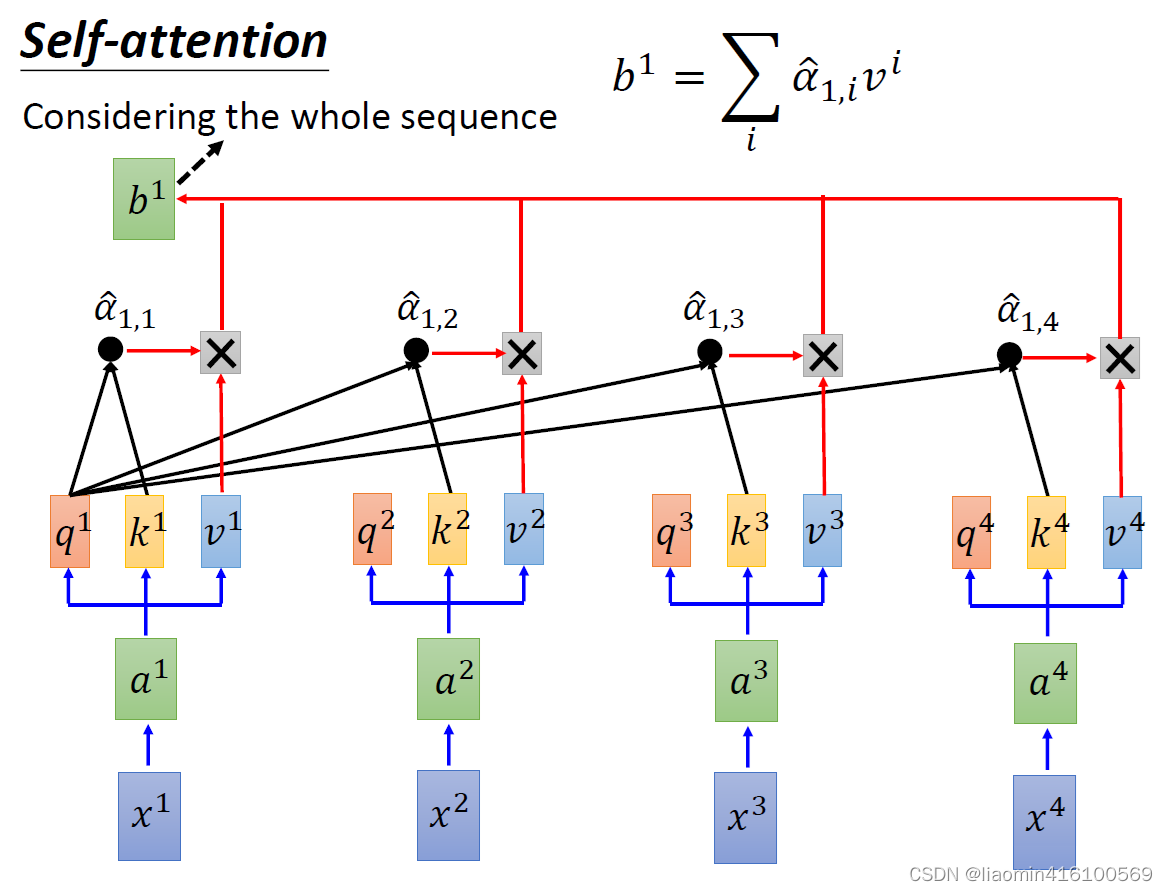
同样的计算过程,我们对剩下的a都进行一次,就可以得到
b
2
b^2
b2,
b
3
b^3
b3,
b
4
b^4
b4,每个b都是综合了每个a之间的相关性计算出来的,这个相关性就是我们所说的注意力机制,。那么我们将这样的计算层称为self-attention layer。
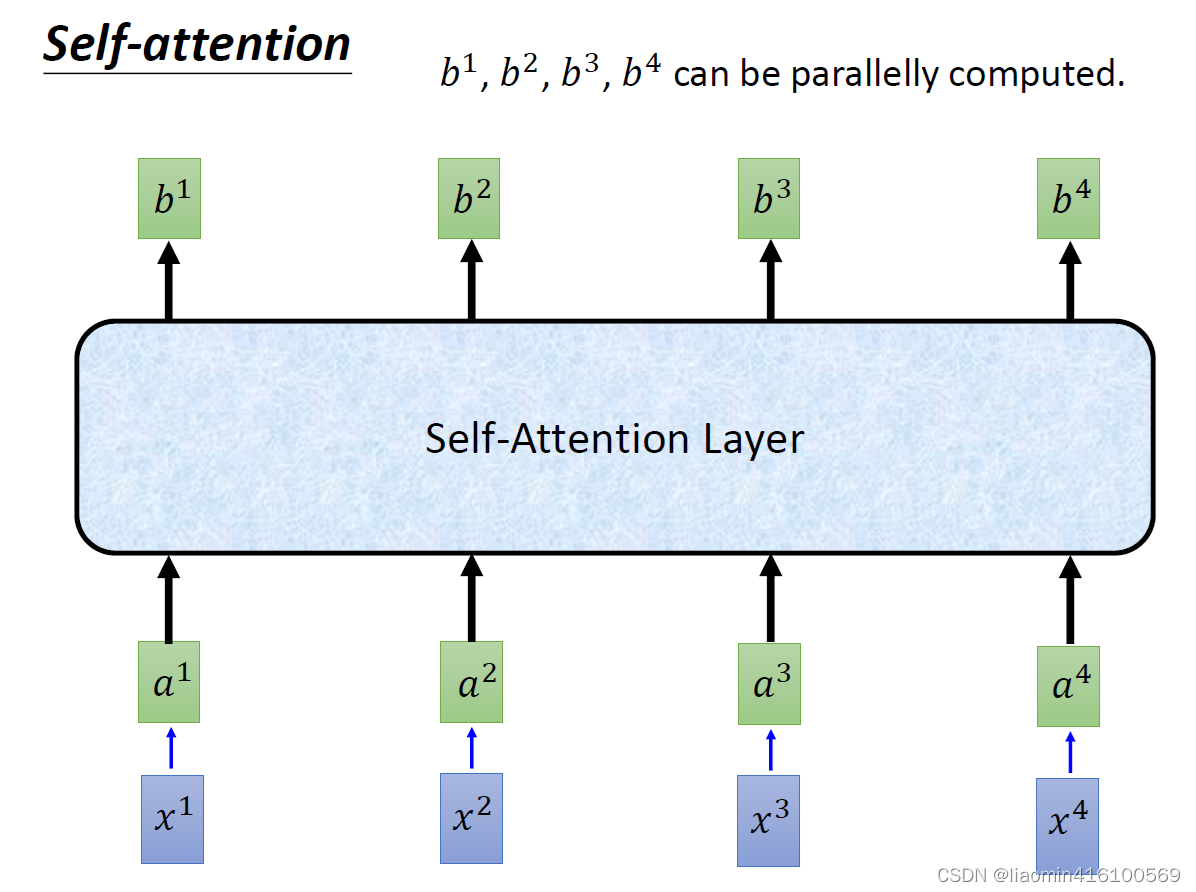
我们把一个句子中的每个字代入上图的
x
1
x^1
x1,
x
2
x^2
x2 ,
x
3
x^3
x3,
x
4
x^4
x4
矩阵计算
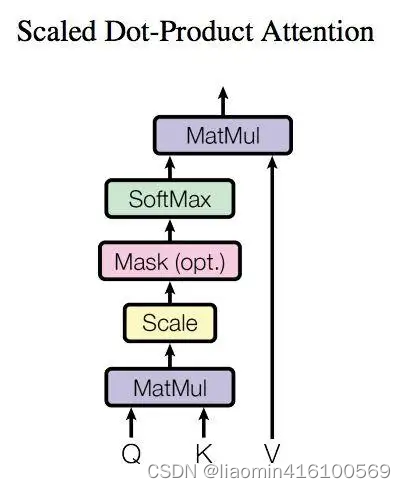
上图是 Self-Attention 的结构,在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。在实际中,Self-Attention 接收的是输入(单词的表示向量x组成的矩阵X) 或者上一个 Encoder block 的输出。而Q,K,V正是通过 Self-Attention 的输入进行线性变换得到的。
Q,K,V计算
输入矩阵X=position encoding+word embedding,其中维度d_model,行为句子中单词的个数。
需要知道x的格式参考:Word2Vec实例
Self-Attention 的输入用矩阵X进行表示,则可以使用线性变阵矩阵WQ,WK,WV计算得到Q,K,V。计算
如下图所示,注意 X, Q, K, V 的每一行都表示一个单词,WQ,WK,WV是一个d_model(输入矩阵的列)行的线性变阵参数,X的每一行都会都会有自己的QKV,比如
X
1
X_1
X1对应
Q
1
,
K
1
,
V
1
Q_1,K_1,V_1
Q1,K1,V1,即
X
n
X_n
Xn对应
Q
n
,
K
n
,
V
n
Q_n,K_n,V_n
Qn,Kn,Vn,所以 X, Q, K, V 的每一行都表示一个单词。
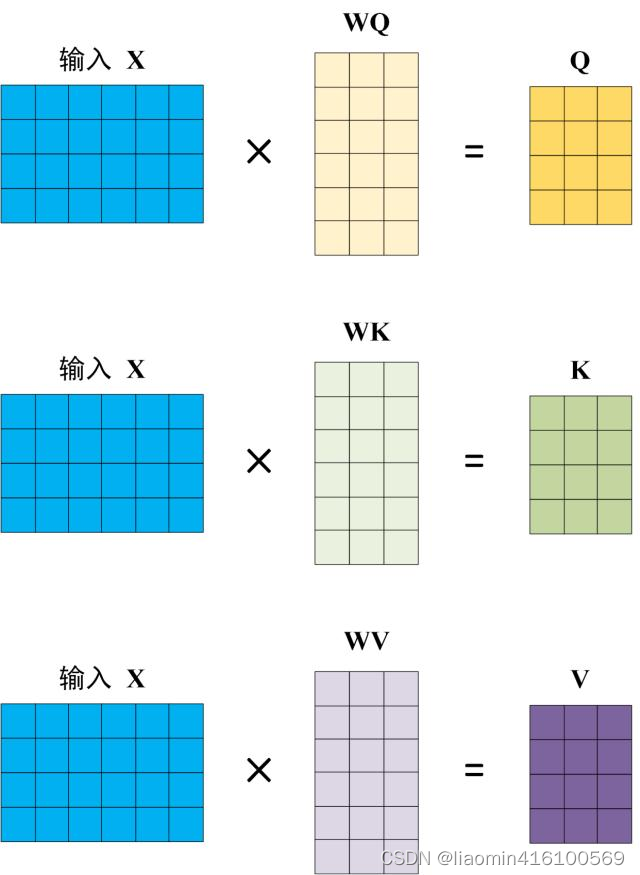
Self-Attention 的输出
得到矩阵 Q, K, V之后就可以计算出 Self-Attention 的输出了,计算的公式如下:

公式中计算矩阵Q和K每一行向量的内积,为了防止内积过大,因此除以
d
k
d_k
dk的平方根,缩放注意力,以使得注意力分布的方差在不同维度上保持一致,从而更好地控制梯度的稳定性。。Q乘以K的转置后,得到的矩阵行列数都为 n,n 为句子单词数,这个矩阵可以表示单词之间的 attention 强度。下图为Q乘以
K
T
K^T
KT, 1234 表示的是句子中的单词。

得到
Q
K
T
QK^T
QKT之后,使用 Softmax 计算每一个单词对于其他单词的 attention 系数,公式中的 Softmax 是对矩阵的每一行进行 Softmax,即每一行的和都变为 1.
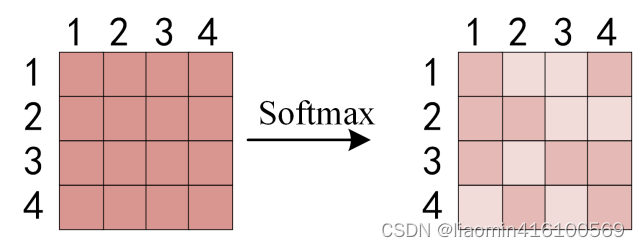
得到 Softmax 矩阵之后可以和V相乘,得到最终的输出Z。
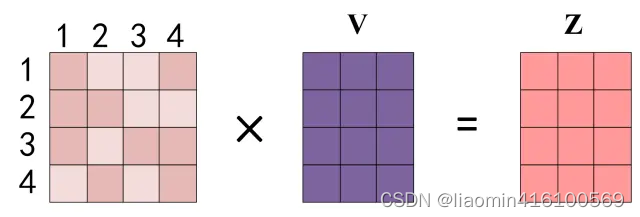
上图中 Softmax 矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数,最终单词 1 的输出
Z
1
Z_1
Z1等于所有单词 i 的值
V
i
V_i
Vi根据 attention 系数的比例加在一起得到,如下图所示:

优势
从self-attention的原理中可以看出,这一层需要学习的参数只有
W
q
W^q
Wq ,
W
k
W^k
Wk,
W
v
W^v
Wv,大部分变量来自于内部计算得出来的,所以它的参数量少但每个参数所涵盖的信息多,这是它的第一个优点。
每个b的计算都是独立的,这一点相比之前的RNN来说很不一样,RNN是需要等前面的
a
1
a^1
a1算完了才能算
a
2
a^2
a2,是串行的。所以RNN无论是训练还是推理,都会因为不能计算并行而变慢,这是它的的第二个优点。
RNN的一个最大的问题是:前面的变量在经过多次RNN计算后,已经失去了原有的特征。越到后面,最前面的变量占比就越小,这是一个很反人类的设计。而self-attention在每次计算中都能保证每个输入变量 a的初始占比是一样的,这样才能保证经过self-attention layer计算后他的注意力系数是可信的。
所以总结下来,它的三个优点分别是:
- 需要学习的参数量少
- 可以并行计算
- 能够保证每个变量初始占比是一样的
Multi-head self-attention
原理
通俗易懂理解
multi-head self-attention,所谓head也就是指一个a 衍生出几个q , k , v 。上述所讲解的self-attention是基于single-head的。以2 head为例:
首先,
a
i
a^i
ai先生成
q
1
q^1
q1,
k
1
k^1
k1,
v
1
v^1
v1,然后,接下来就和single-head不一样了,
q
i
q^i
qi生成
q
i
,
1
,
q
i
,
2
q^{i,1},q^{i,2}
qi,1,qi,2生成的方式有两种:
- q i q^i qi乘上一个 W q , 1 W^{q,1} Wq,1得到 q i , 2 q^{i,2} qi,2,这个和single-head的生成是差不多的;
- q i q^i qi直接从通道维,平均拆分成两个,得到 q i , 1 , q i , 2 q^{i,1},q^{i,2} qi,1,qi,2
这两种方式,在最后结果上都差不多。至于为啥,后面会讲一下原因。
那么这里的图解使用第1个方式,先得到
q
i
,
1
q^{i,1}
qi,1,
k
i
,
1
k^{i,1}
ki,1,
v
i
,
1
v^{i,1}
vi,1。对
a
j
a^j
aj做同样的操作得到
,对
a
j
a^j
aj做同样的操作得到
q
j
,
1
q^{j,1}
qj,1,
k
j
,
1
k^{j,1}
kj,1,
v
j
,
1
v^{j,1}
vj,1。这边需要注意的一点,
q
i
,
1
q^{i,1}
qi,1是要和
k
j
,
1
k^{j,1}
kj,1做矩阵乘法,而非
k
j
,
2
k^{j,2}
kj,2,一一对应。后面计算就和single-head一样了,最后得到
b
i
,
1
b^{i,1}
bi,1

第二步,对
q
i
,
2
q^{i,2}
qi,2,
k
i
,
2
k^{i,2}
ki,2,
v
i
,
2
v^{i,2}
vi,2做一样的操作,得到
b
i
,
2
b^{i,2}
bi,2

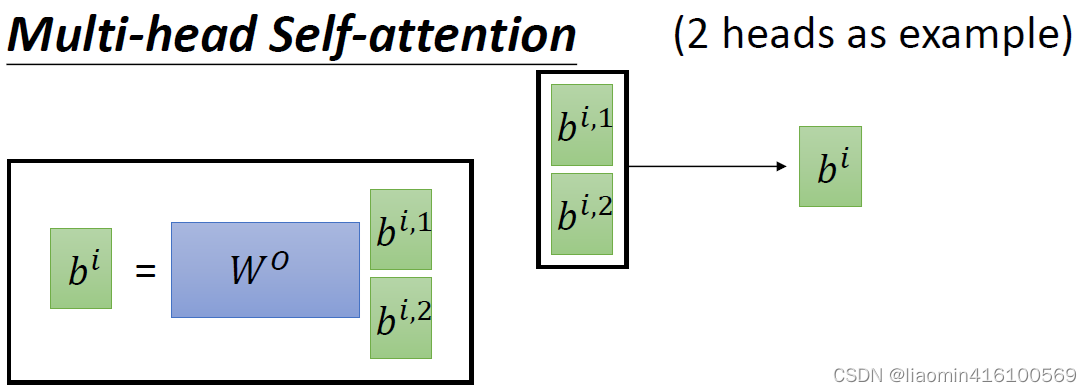
这里我们算出的
b
i
,
1
b^{i,1}
bi,1,
b
i
,
2
b^{i,2}
bi,2是同维度的,我们可以将其concat在一起,再通过一个
W
0
W^0
W0把他转成想要的维度。这也就不难理解,为什么说multi-head的两种生成方式是一样的,因为最终决定是输出维度的是
W
o
W^o
Wo。我们可以将multi-head的过程看成是cnn中的隐藏层,multi-head的数量也就对应着Conv2D的filter数量,每一个head各司其职,提取不同的特征。
矩阵计算
我们已经知道怎么通过 Self-Attention 计算得到输出矩阵 Z,而 Multi-Head Attention 是由多个 Self-Attention 组合形成的,下图是论文中 Multi-Head Attention 的结构图。
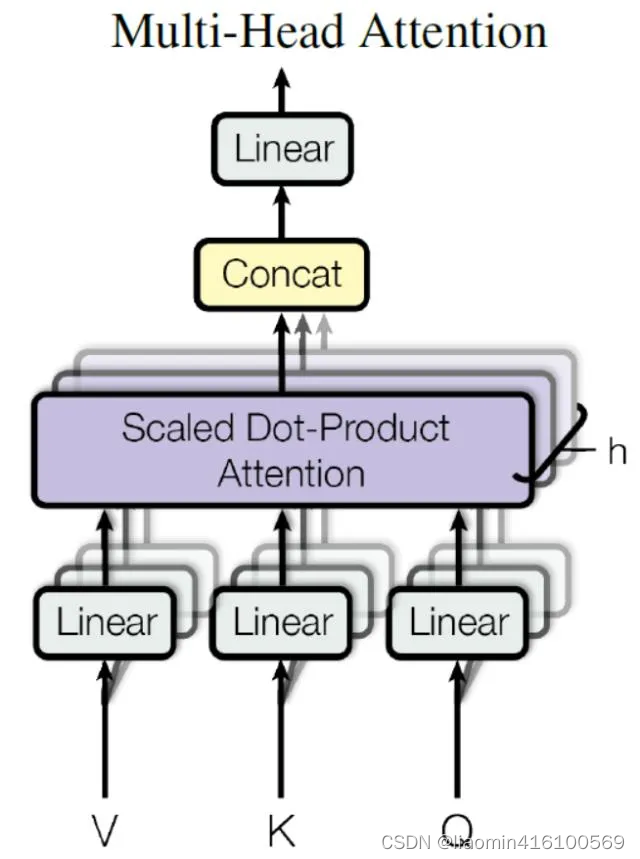
从上图可以看到 Multi-Head Attention 包含多个 Self-Attention 层,首先将输入X分别传递到 h 个不同的 Self-Attention 中,计算得到 h 个输出矩阵Z。下图是 h=8 时候的情况,此时会得到 8 个输出矩阵Z。
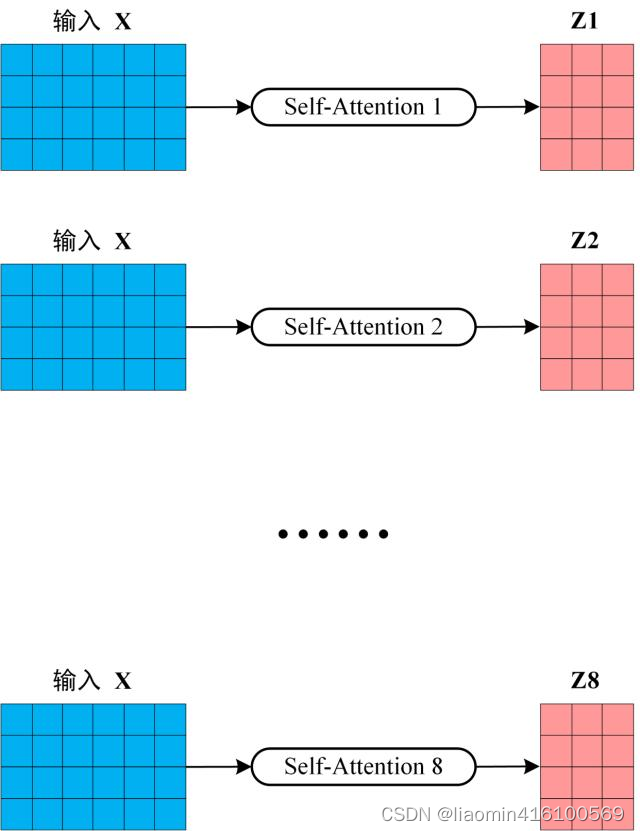
得到 8 个输出矩阵
Z
1
Z_1
Z1到
Z
8
Z_8
Z8之后,Multi-Head Attention 将它们拼接在一起 (Concat),然后传入一个Linear层,得到 Multi-Head Attention 最终的输出Z。
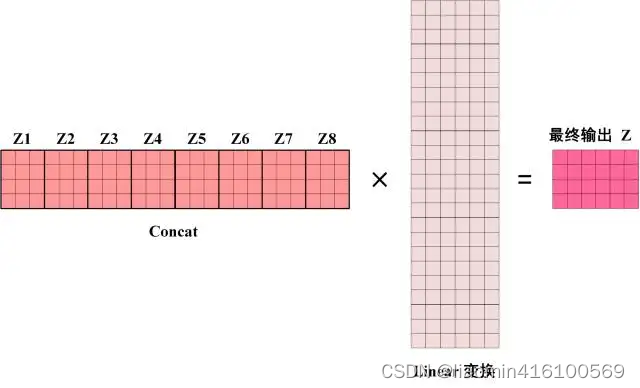
可以看到 Multi-Head Attention 输出的矩阵Z与其输入的矩阵X的维度是一样的。
代码实现
import torch
import torch.nn as nn
import torch.nn.functional as F
class SelfAttention(nn.Module):
def __init__(self, embed_size, num_heads):
"""
初始化 SelfAttention 层
参数:
embed_size (int): 输入特征的维度
num_heads (int): 注意力头的数量
"""
super(SelfAttention, self).__init__()
self.embed_size = embed_size
self.num_heads = num_heads
self.head_dim = embed_size // num_heads
# 确保 embed_size 能被 num_heads 整除
assert (
self.head_dim * num_heads == embed_size
), "Embedding size needs to be divisible by heads"
# 初始化线性层
self.values = nn.Linear(self.head_dim, self.head_dim, bias=False)
self.keys = nn.Linear(self.head_dim, self.head_dim, bias=False)
self.queries = nn.Linear(self.head_dim, self.head_dim, bias=False)
self.fc_out = nn.Linear(num_heads * self.head_dim, embed_size)
def forward(self, values, keys, query):
"""
前向传播函数
参数:
values (Tensor): 值的张量,形状为 (batch_size, value_len, embed_size)
keys (Tensor): 键的张量,形状为 (batch_size, key_len, embed_size)
query (Tensor): 查询的张量,形状为 (batch_size, query_len, embed_size)
返回:
out (Tensor): 输出张量,形状为 (batch_size, query_len, embed_size)
"""
# 获取张量的大小
N = query.shape[0]
value_len, key_len, query_len = values.shape[1], keys.shape[1], query.shape[1]
# 将输入张量按头数和头维度进行切分
values = values.reshape(N, value_len, self.num_heads, self.head_dim)
keys = keys.reshape(N, key_len, self.num_heads, self.head_dim)
queries = query.reshape(N, query_len, self.num_heads, self.head_dim)
# 通过线性层进行变换
values = self.values(values)
keys = self.keys(keys)
queries = self.queries(queries)
# 计算点积注意力
energy = torch.einsum("nqhd,nkhd->nhqk", [queries, keys]) # batch_size, num_heads, query_len, key_len
# 计算注意力权重
attention = torch.nn.functional.softmax(energy / (self.embed_size ** (1/2)), dim=3)
# 将注意力权重应用到值上
out = torch.einsum("nhql,nlhd->nqhd", [attention, values]).reshape(
N, query_len, self.num_heads * self.head_dim
)
# 合并多个头并通过线性层进行变换
out = self.fc_out(out)
return out