三维点云处理-聚类（下）

接着前一部分数据聚类方法的介绍，由于K-means和GMM方法都是基于欧式距离信息处理的，两者分别以圆形和椭圆形来作为数据的聚类分割方式，这种情况下会导致环形图和月牙图数据分割不准确，因此进一步的介绍一种谱聚类方法，该方法是基于图论的，关注的是数据与数据之间的连接性，聚类分割效果相对更好。并且除了谱聚类外，也会对 Mean-shift 和 DBSCAN 方法进行简单介绍。
这里推荐一篇关于讲解谱聚类方法的博客：一文带你深入浅出地搞懂谱聚类

1. Spectral clustering（谱聚类）

谱聚类的思想来源于图论，谱指的是矩阵的特征值。它将待聚类数据集中的每一个样本看做是图中的一个顶点，顶点与顶点相连的边上有权重，权重的大小表示样本之间的相似程度。同一类的顶点之间相似性较高，在图论中体现为同一类的顶点之间连接边的权重较大，而不同类的顶点之间连接边的权重较小。基于这样的特性，谱聚类方法的目标就是找到一种切割图的方法，使得切割之后各个子图内的权重很大，子图间的权重很小。

如上图所示， $W_{ij}$ 表示的就是一条权重比较小的边，对应于连接不同类顶点之间的权重较小，此时在右图中关于 $W_{ij}$ 做切割时就可以得到如左图所示的两个类。

1.1 算法流程

假设给定一个样本集 $X=\{ x_1,x_2,...,x_n \}$ ，其中每一个样本 $x_i \in R^m$ ，那么如何使用谱聚类方法将它们划分为 k 类呢？

主要流程如下：（以非标准化的Laplacian矩阵为例）

将样本集作为顶点集建图，并构建顶点间的邻接矩阵 $\in \Reals^{n \times n}$
构建度与度矩阵（Degree Matrix）D
计算 Laplacian 矩阵 L
计算 L 矩阵特征值最小的 k 个特征向量 $v_1,v_2,...,v_k \space\space of \space L$
将 k 个特征向量构成新的矩阵 $\in \Reals^k$ ，V 矩阵的每一行 $y_i \in \Reals^k,i=1,2,...,n$ 可以看做是对应 $x_i$ 降至 k 维空间后的形式；
使用k-means方法将数据 $\{ y_i \in \Reals^k \}$ 划分为 k 类；

1.1.1 邻接矩阵 W 构建

对于一副无向图 G=(V, E) ，V表示顶点的集合，E表示边的集合，通常有两个比较重要的概念：图的邻接矩阵 和顶点的度。所有顶点之间的权重组成一个 n x n 的矩阵，称为邻接矩阵，也叫权重矩阵，即：
$\begin{bmatrix} w_{11} & w_{12} & \cdots & w_{1n} \\ w_{21} & w_{22} & \cdots & w_{2n} \\ \vdots& \vdots & \ddots & \vdots \\ w_{n1} & w_{n2} & \cdots & w_{nn} \end{bmatrix}$
对于无向图，顶点 $v_i$ 和 $v_j$ 之间的权重 $w_{ij}$ 和顶点 $v_j$ 和 $v_i$ 之间的权重 $w_{ji}$ 是一样的，即 $w_{ij}=w_{ji}$ ，因此 W 矩阵为对称矩阵，即 $W=W^T$ 。这里简单介绍三种相似矩阵的构建方法：

$\varepsilon$ - 近邻法

该方法使用欧式距离 $d(v_i,v_j)$ 计算两个顶点之间的距离，然后设定一个阈值 $\varepsilon$ ，使得：
$w_{ij} = \begin{cases} 0, & \text{if $s_{ij} > \varepsilon$ } \\ d(v_i,v_j), & \text{if $s_{ij} \le \varepsilon$ } \end{cases}$
一般来说，距离越近即相似性越高，因此可以考虑选择 $w_{ij}=max(d(v_i,v_j))-d(v_i,v_j)$ 来保证距离值和权重之间的一致性。

k - 近邻法

该方法选取当前顶点的 k 个近邻点，该顶点与这 k 个顶点的权重都大于 0，但需要注意的是，如果点 $v_i$ 在点 $v_j$ 的 k 个近邻点中，不一定能够保证 $v_j$ 也在 $v_i$ 的 k 个近邻点中，这样得到的相似矩阵无法满足对称的要求。因此需要对相似矩阵的构建方法进行限制，常用的方式有两种：

方式一：顶点 $v_i$ 和顶点 $v_j$ 只要其中一个点在另一个点的 k 个近邻中，就令 $w_{ij}=w_{ji}$ ，如果两个都不满足对方的 k 近邻关系，则令 $w_{ij}=w_{ji}=0$ ，因此：

方式二：顶点 $v_i$ 和顶点 $v_j$ **必须同时满足双方的 k 近邻关系时，**才令 $w_{ij}=w_{ji}$ ，否则，只要有一方不在另一方的 k 个近邻中，就令 $w_{ij}=w_{ji}=0$ ，因此：

全连接法

该方法将所有的顶点都连接起来，然后通过度量空间中某种对称度量算子来计算顶点之间的相似度。比如使用顶点之间的欧式距离，同时为了保证距离越近相似度越高，即权重越大的特性，可以采用如下方式进行表示：
$w_{ij}=w_{ji}=max(d(v_i,v_j))-d(v_i,v_j)$

1.1.2 度与度矩阵 D 构建

在数据结构中，度是指与该顶点直接连接的顶点的个数。如果相似性矩阵 W 是表示顶点间连接关系的二值矩阵，那么度矩阵的值与最初的定义一致。但进一步，如果相似性矩阵 W 中记录的是顶点和顶点所连边的权重，那么对于顶点 $d_i,i=1,2,...,n$ ，可以将度定义为该顶点所连边的权重之和，即
$d_i =\sum_{j-1}^n w_{ij}$ 即对于第 i 个顶点 $v_i$ ，其对应的度就是邻接矩阵 W 中第 i 行的和，即度矩阵 D 的形式如下：

给定顶点 V 的一个子集 $\sub V$ ，将顶点集V中子集A之外所有顶点组成的集合称为 A 的补集，记为 $\bar{A}$ 。子集的大小有两种定义：

子集内顶点的个数，记作 $∣ A ∣$
子集内所有顶点的度之和，记作 $vol(A)=\sum_{v_i \in A}d_i$

1.1.3 拉普拉斯矩阵 L 构建

拉普拉斯矩阵一般分为非标准化的拉普拉斯矩阵和标准化的拉普拉斯矩阵，前者倾向于将聚类划分为数量相近的顶点集，而后者更倾向于将聚类划分为密度相近的顶点集。

非规范化的拉普拉斯矩阵
$L = D - W$
其中， D 对度矩阵，W 为相似矩阵。显然，由于 D 和 W 都是对称矩阵，所有两种组合后形成的 L 矩阵也是一个对称矩阵。
标准化的拉普拉斯矩阵
常见的标准化表达形式有两种， $L_{sym}$ 和 $L_{rw}$ ，两者的定义形式如下： $L_{sym}=D^{-1/2} L D^{-1/2} = I - D^{-1/2} W D^{-1/2}$
$L_{rw}= D^{-1}L = I-D^{-1}W$
其中， $L_{sym}$ 是一个对称矩阵，sym指的是symmertic的缩写；而 $L_{rw}$ 不是对称矩阵，rw指的是random walk，是一种基于随机游走的拉普拉斯矩阵。

1.1.4 聚类个数 k 如何确定

谱聚类有一个比较好的特性就是：谱聚类的特征值中，较小的特征值对应的特征向量往往包含了图的主要结构信息。因此，可以观察特征值的分布，寻找一个“拐点”或“间隙”，即特征值突然变小的位置。这个位置之前的特征值数量可能对应着数据的聚类数量。

1.2 数学原理补充

这部分会简单说明一下引入拉普拉斯矩阵的原因及矩阵性质，以及如何进行图分割。

1.2.1 为什么要引入拉普拉斯矩阵 L ？

因为 L 矩阵具有良好的特性，能够帮助聚类。

特征值为 0 的数量表示了独立分区的数量；
相对应的特征向量代表哪些点属于该连通区域（即特征矩阵包含了聚类结果的信息）。

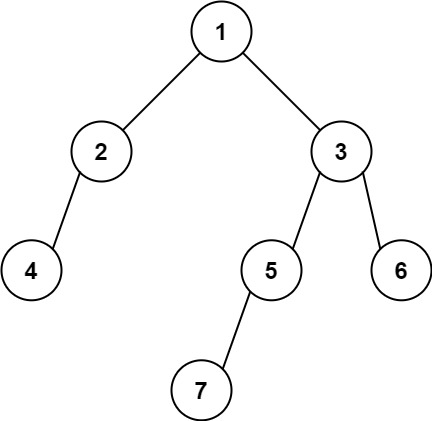
如上图，当无向图上存在左右两块分区时，L矩阵有两个 0 特征值，即有两个独立分区，且0特征值对应的特征向量如右图所示，特征向量中的值也包含了两个独立分区中顶点相连的情况：{3, 4, 5, 6, 7} 和 {0, 1, 2, 8, 9}。

如上图，当只存在一个连通区域时，仅有一个 0 特征值。之前为0的第二特征值数值上出现了一些变化，其对应的特征向量变换后，可以看出：正值对应的顶点为一个分区{3, 4, 5, 6, 7}，负值对应的顶点为另一个分区{0, 1, 2, 8, 9}。

1.2.2 命题1 - 拉普拉斯矩阵L的性质

定理1：对于任意的向量 $\in \Reals^n$ ，都有： $f^TLf = \frac{1}{2}\sum_{i=1}^n \sum_{j=1}^n w_{ij} (f_i - f_j)^2$ 证明如下：
定理2：L 是一个对称和半正定矩阵。
证明如下：

对称性：L=D-W，D和W均为对称矩阵，因此 L 也是对称矩阵；
半正定性：由定理 1 可知， $f^T L f \ge 0$ 恒成立，所以 L 具有半正定性。

定理3：L 的最小特征值为0，且对应的特征向量为常数向量。
证明如下：

上式中，当 $f_i = f_j$ 时，上式恒成立。

定理4：L 有 n 个非负、实数特征值** ** $\lambda_1 \le \lambda_2 \le ... \le \lambda_n$

1.2.3 命题2 - 连通域数量

L 矩阵有几个特征值为 0 的特征向量，取决于无向图 G 有多少个连通域。

当 k = 1时，

$f^TLf = (f_1-f_2)^2 + (f_1-f_4)^2 + (f_2 - f_3)^2 + (f_3-f_4)^2 + (f_4-f_5)^2 + (f_5-f_6)^2 = 0$
整理可得： $f_1 = f_2 = f_3 = f_4 = f_5 = f_6$ 即最小特征值对应的特征向量为常数向量。
当 k > 1时，L矩阵有 k 个不相交的连通区域，对于每个连通子区域 $A_i$ ，其对应的拉普拉斯矩阵 $L_i$ 和 k=1 时的L具有相同的性质，即每个连通子图 $A_i$ 对应的拉普拉斯矩阵 $L_i$ 都有一个0特征值及其常量特征向量。

1.2.4 图切割方法

基于图论的聚类方法是希望找到一种切割方法，使得切割后各个组之间的相似性很小，同时组内数据之间的相似性很大。假设给定一个无向图 G 和邻接矩阵 W，将其聚类分割成不同的组：
假设划分为两个独立分区， $\sub V$ ：

假设划分为 k 个独立分区， $A_1, A_2,...,A_k$ ：

常见的分割标准有两种：非标准化谱聚类和标准化谱聚类。

非标准化谱聚类 — 近似 RatioCut
标准化谱聚类 — 近似 NormalizedCut

1.2.5 近似 RatioCut (k=2)

问题可以简化为：

给定一个子集 $\sub V$ ，构造向量 $f=[f_1,f_2,...,f_n]^T \in \Reals^n$ ：

应用定理1 构造向量 f :

此外，① f 是与常数向量正交的向量。② 向量 f 的范数为： $\sqrt{\smash[b]{n}}$

所以 RatioCut 的问题可以进一步转化为：

但由于 f 是自己假设构造的，实际上并不知道它是什么样的，因此干脆去掉这个条件，来对问题做一个近似，也就是近似 RatioCut，这里结合到前面构造的矩阵形式 $f^TLf$ ，考虑使用瑞利熵来进行求解近似的 f 向量：

在得到 f 向量之后，根据 L 矩阵的性质，我们知道第一个特征向量包含了连通域的数量信息，第二个特征向量包含了点的分类信息，即Graph Cut信息，此时就可以使用k-means方法来对其进行聚类了。

进一步，当 k 大于等于2时，同理，把f变成矩阵进行处理。

1.3 代码练习

class Spectral {
public:
    enum class ADJACENCY_METHOD{
        NEAREST_NEIGHBOR,
        K_NEIGHBORHOOD_GRAPH,
        FULL_CONNECT
    };

    enum class NORMALIZED_LAPLACIAN{
        NONE,
        SYM,    // L = D^{-1/2} L D^{-1/2} = I - D^{-1/2} W D^{-1/2}
        RW      // D^{-1} L = I - D^{-1}W
    };

    bool input(const Eigen::MatrixXd& input_matrix);
    bool compute(int k = 0,
                 int max_step = 100,
                 double min_update_size = 0.01,
                 ADJACENCY_METHOD adjecency_method = ADJACENCY_METHOD::NEAREST_NEIGHBOR,
                 NORMALIZED_LAPLACIAN normalized_laplacian = NORMALIZED_LAPLACIAN::RW);
    std::vector<Cluster>& get_clusters();
    void print_clusters();
    void set_neighbor_k(int neighbor_k_);

private:
    bool build_adjacency_matrix(ADJACENCY_METHOD adjacency_method);
    bool build_adjacency_matrix_full_connect();
    bool build_adjacency_matrix_nearest_neighbor();
    bool build_adjacency_matrix_k_neighborhood_graph();

    bool build_Laplacian_matrix(NORMALIZED_LAPLACIAN normalized_laplacian);
    bool build_Laplacian_matrix_NONE();
    bool build_Laplacian_matrix_RW();
    bool build_Laplacian_matrix_SYM();

    bool build_V_matrix(int k = 0);

private:
    Eigen::MatrixXd _data;
    Eigen::MatrixXd _W;
    Eigen::MatrixXd _L;
    Eigen::MatrixXd _V;

    std::vector<Cluster> _clusters;
    int _cluster_num;
    int _neighbor_k = 0;
};

#include "Clustering/spectral.h"

#include <Eigen/Dense>

bool Spectral::input(const Eigen::MatrixXd& input_matrix){
    _data = input_matrix;
    return true;
}

void Spectral::set_neighbor_k(int neighbor_k_) {
    _neighbor_k = neighbor_k_;
}


bool Spectral::compute(int k, int max_step,
                       double min_update_size,
                       ADJACENCY_METHOD adjacency_method,
                       NORMALIZED_LAPLACIAN normalized_laplacian){
    // 构建相似（权重）矩阵 W
    if(!build_adjacency_matrix(adjacency_method)){
        std::cerr << "build_adjacency_matrix failed!" << std::endl;
        return false;
    }
    // 计算Laplacian矩阵
    if(!build_Laplacian_matrix(normalized_laplacian)){
        std::cerr << "build_Laplacian_matrix fialed!" << std::endl;
        return false;
    }

    // 计算V矩阵
    if(!build_V_matrix(k)){
        std::cerr << "build_V_matrix failed!" << std::endl;
        return false;
    }

    // 使用k-means聚类
    KMeans k_means;
    k_means.input(_V.transpose());      // 注意输入的是 特征向量V 的转置！！！
    k_means.compute(_cluster_num, max_step, min_update_size);
    _clusters = k_means.get_clusters();
    print_clusters();

    return true;
}

bool Spectral::build_adjacency_matrix(ADJACENCY_METHOD adjacency_method){
    // 根据参数选择相似矩阵构建方法
    if(adjacency_method == ADJACENCY_METHOD::FULL_CONNECT){
        std::cout << "build_adjacency_matrix: FULL_CONNECT" << std::endl;
        return build_adjacency_matrix_full_connect();
    }else if(adjacency_method == ADJACENCY_METHOD::NEAREST_NEIGHBOR){
        std::cout << "build_adjacency_matrix: NEAREST_NEIGHBOR" << std::endl;
        return build_adjacency_matrix_nearest_neighbor();
    }else if(adjacency_method == ADJACENCY_METHOD::K_NEIGHBORHOOD_GRAPH){
        std::cout << "build_adjacency_matrix: K_NEIGHBORHOOD_GRAPH" << std::endl;
        return build_adjacency_matrix_k_neighborhood_graph();
    }else{
        std::cerr << "adjacency_method invalid!" << std::endl;
        return false;
    }

    return true;
}

bool Spectral::build_adjacency_matrix_full_connect(){
    // 计算数据点间最大距离
    double max_weight = 0.0;
    for(size_t i = 0; i < _data.cols(); ++i){
        const Eigen::VectorXd d1 = _data.col(i);
        for(size_t j = 0; j < _data.cols(); ++j){
            if(i == j) continue;
            const Eigen::VectorXd d2 = _data.col(j);
            if((d1 - d2).norm() > max_weight){
                max_weight = (d1 - d2).norm();
            }
        }
    }

    // 计算点间权重
    _W.resize(_data.cols(), _data.cols());
    for(size_t i = 0; i < _data.cols(); ++i){
        const Eigen::VectorXd d1 = _data.col(i);
        for(size_t j = 0; j < _data.cols(); ++j){
            if(i == j){
                _W(i, j) = 0;
                continue;
            }

            const Eigen::VectorXd d2 = _data.col(j);
            _W(i, j) = max_weight - (d1 - d2).norm();
        }
    }

    return true;
}

// 以点云总量的一定比例作为邻域大小
bool Spectral::build_adjacency_matrix_nearest_neighbor(){
    // 定义 k 和 kd-tree的叶子大小
    int leaf_size = (_data.cols() > 10) ? 0.1 * _data.cols() : 2;
    int knn_size = (_data.cols() > 25) ? 0.25 * _data.cols() : 4;

    // 计算最大距离
    double max_weight = 0.;
    for(size_t i = 0; i < _data.cols(); ++i){
        const Eigen::VectorXd d1 = _data.col(i);
        for(size_t j = 0; j < _data.cols(); ++j){
            if(i == j) continue;
            
            const Eigen::VectorXd d2 = _data.col(j);
            if((d1 - d2).norm() > max_weight){
                max_weight = (d1 - d2).norm();
            }
        }
    }

    std::cout << "max_weight: " << max_weight << std::endl;
    std::cout << "leaf_size: " << leaf_size << std::endl;
    std::cout << "knn_size: " << knn_size << std::endl;

    // 计算相似矩阵 W
    _W.resize(_data.cols(), _data.cols());

    KDTreeAVLNearestNeighbors nn;
    nn.set_data(_data, leaf_size);

    for(size_t i = 0; i < _data.cols(); ++i){
        const Eigen::MatrixXd d1 = _data.col(i);
        KNNResultNumber knn_result(knn_size);
        nn.KNN_search_number(d1, knn_result);
        std::vector<DistanceValue> dv = knn_result.get_distance_value();
        // 只负责更新邻域点数据
        for(int j = 0; j < dv.size(); ++j){
            if(dv[j].value == i){
                _W(i, dv[j].value) = 0;
                continue;
            }

            const Eigen::VectorXd d2 = _data.col(dv[j].value);
            _W(i, dv[j].value) = max_weight - (d1 - d2).norm();
        }
    }

    return true;
}

// 指定近邻点数量 neighbor_k
bool Spectral::build_adjacency_matrix_k_neighborhood_graph(){
    // 定义 k 和 kd-tree的叶子大小
    int leaf_size = (_data.cols() > 10) ? 0.1 * _data.cols() : 2;
    int knn_size;
    if(_neighbor_k > 0){
        knn_size = _neighbor_k;
    }else{
        knn_size = (_data.cols() > 10) ? 0.25 * _data.cols() : 4;
    }

    // 计算最大距离
    double max_weight = 0.;
    for(size_t i = 0; i < _data.cols(); ++i){
        const Eigen::VectorXd d1 = _data.col(i);
        for(size_t j = 0; j < _data.cols(); ++j){
            if(i == j) continue;
            
            const Eigen::VectorXd d2 = _data.col(j);
            if((d1 - d2).norm() > max_weight){
                max_weight = (d1 - d2).norm();
            }
        }
    }

    // 计算相似矩阵 W
    _W.resize(_data.cols(), _data.cols());

    KDTreeAVLNearestNeighbors nn;
    nn.set_data(_data, leaf_size);

    for(size_t i = 0; i < _data.cols(); ++i){
        const Eigen::MatrixXd d1 = _data.col(i);
        KNNResultNumber knn_result(knn_size);
        nn.KNN_search_number(d1, knn_result);
        std::vector<DistanceValue> dv = knn_result.get_distance_value();
        // 只负责更新邻域点数据
        for(int j = 0; j < dv.size(); ++j){
            if(dv[j].value == i){
                _W(i, dv[j].value) = 0;
                continue;
            }

            const Eigen::VectorXd d2 = _data.col(dv[j].value);
            _W(i, dv[j].value) = max_weight - (d1 - d2).norm();
        }
    }

    return true;
}

bool Spectral::build_Laplacian_matrix(NORMALIZED_LAPLACIAN normalized_laplacian){
    // 根据参数选择Laplacian计算方法
    if(normalized_laplacian == NORMALIZED_LAPLACIAN::NONE){
        std::cout << "build_Laplacian_matrix: NONE" << std::endl;
        return build_Laplacian_matrix_NONE();
    }else if(normalized_laplacian == NORMALIZED_LAPLACIAN::RW){
        std::cout << "build_Laplacian_matrix: RW" << std::endl;
        return build_Laplacian_matrix_RW();
    }else if(normalized_laplacian == NORMALIZED_LAPLACIAN::SYM){
        std::cout << "build_Laplacian_matrix: SYM" << std::endl;
        return build_Laplacian_matrix_SYM();
    }else{
        std::cerr << "normalized_laplacian method: invalid" << std::endl;
        return false;
    }

    return true;
}

bool Spectral::build_Laplacian_matrix_NONE(){
    // 计算度与度矩阵 D
    Eigen::VectorXd d = _W.rowwise().sum();
    Eigen::MatrixXd D = Eigen::MatrixXd::Zero(_data.cols(), _data.cols());
    for(size_t i = 0; i < _data.cols(); ++i){
        D(i, i) = d(i);
    }

    // 计算Laplacian矩阵 L = D - W
    _L = D - _W;
    return true;
}

bool Spectral::build_Laplacian_matrix_RW(){
    // 计算度与度矩阵 D
    Eigen::VectorXd d = _W.rowwise().sum();
    Eigen::MatrixXd D = Eigen::MatrixXd::Zero(_data.cols(), _data.cols());
    for(size_t i = 0; i < _data.cols(); ++i){
        D(i, i) = d(i);
    }    

    // 计算Laplacian矩阵 L = D^{-1}L = I - D^{-1}W
    Eigen::MatrixXd I = Eigen::MatrixXd::Identity(_data.cols(), _data.cols());
    _L = I - D.inverse() * _W;
    return true;
}

bool Spectral::build_Laplacian_matrix_SYM(){
    // 计算度与度矩阵 D
    Eigen::VectorXd d = _W.rowwise().sum();
    Eigen::MatrixXd D = Eigen::MatrixXd::Zero(_data.cols(), _data.cols());
    for(size_t i = 0; i < _data.cols(); ++i){
        D(i, i) = d(i);
    }

    // 计算D的逆平方根矩阵D_inv_sqrt  
    Eigen::MatrixXd D_inv_sqrt = Eigen::MatrixXd::Zero(_data.cols(), _data.cols());  
    for(size_t i = 0; i < _data.cols(); ++i){  
        if(d(i) > 0){ // 避免除以零  
            D_inv_sqrt(i, i) = 1.0 / std::sqrt(d(i));  
        }  
    } 

    // 方式二：处理可能的零度问题（可选）  
    // d = d.array() + (d.array() == 0).cast<double>() * 1e-10; // 添加一个小的值避免除以零  
    // D.diagonal() = d;  
  
    // // 计算D的逆平方根矩阵D_inv_sqrt  
    // Eigen::MatrixXd D_inv_sqrt = D.array().inverse().sqrt().matrix().asDiagonal();  

    // 计算Laplacian矩阵 L = D^{-1/2}LD^{-1/2} = I - D^{-1/2}WD^{-1/2} 
    Eigen::MatrixXd I = Eigen::MatrixXd::Identity(_data.cols(), _data.cols());
    _L = I - D_inv_sqrt * _W * D_inv_sqrt;  

    return true;
}

bool Spectral::build_V_matrix(int k){
    // 计算特征值及特征向量
    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigen_solver(_L);
    // increased order
    Eigen::VectorXd L_eigen_values = eigen_solver.eigenvalues();
    Eigen::MatrixXd L_eigen_vector = eigen_solver.eigenvectors();
    std::cout << "L_eigen_values: " << L_eigen_values.transpose() << std::endl;


    // 确定 k值
    if(k > 0){
        _cluster_num = k;
    }else{
        if(L_eigen_values.size() < 3){
            _cluster_num = L_eigen_values.size();
        }else{
            // find eigen_gap
            double max_eigen_gap = 0.;
            int idx = -1;
            for(int i = 0; i < L_eigen_values.rows() - 1; ++i){
                double cur_gap = abs(L_eigen_values(i + 1) - L_eigen_values(i));
                if(cur_gap > max_eigen_gap){
                    max_eigen_gap = cur_gap;
                    idx = i;
                }
            }
            if(idx == -1){
                std::cerr << "auto find eigen_gap error!" << std::endl;
                return false;
            }
            _cluster_num = idx + 1;
        }
    }

    std::cout << "number of cluster: " << _cluster_num << std::endl;
    // 计算 V 矩阵
    _V = L_eigen_vector.leftCols(_cluster_num);
    return true;
}

void Spectral::print_clusters(){
    std::cout << "===== spectral clusters =====" << std::endl;
    for (const auto& c : _clusters) {
        std::cout << "cluster " << c.id << ", " << c.center.transpose() << ", " << c.data_index_size << std::endl;
        std::cout << "data index: ";
        for (int i = 0; i < c.data_index_size; ++i) {
            std::cout << c.data_index[i] << " ";
        }
        std::cout << std::endl;
    }
    std::cout << "====================" << std::endl;
}

2. Mean shift（均值漂移算法）

假设给定一堆二维数据点和 k 个半径为 r 的圆，如何放置这些圆可以使得圆中包含的点的数量最多？
方法一：对每一个点进行Radius-NN搜索，计算每个点邻域 r 内的点的数量，排序后找到前 k 个包含点数最多的圆的位置。（计算量较大）
方法二：使用Mean-shift 方法近似求解，先随机找到一个点，计算该点邻域 r 内所有数据点的平均值，再将圆心移动到平均值点所在的位置，不断迭代直至圆心不再移动。（可以作为近似解，但不是最优解）

2.1 算法流程

算法的主要流程如下：（需要给定半径 r ）

随机选择一个点作为半径为 r 圆的圆心；
将圆心移动到圆形邻域的中心；
重复步骤2，直到圆心为止不再移动；
重复步骤1-3，找到多个这样的点，并去除重叠的圆；
如果存在多个圆重叠，选择包含点最多的那个圆。
将数据点划分到距离其最近的圆心（类似于 k-means）

2.2 算法优缺点

算法复杂度： $\cdot n \cdot log(n))$ ，其中 T 表示圆的数量，n 表示样本数量；
优点：能够自动发现类的数量、参数简单（仅需要设置圆的半径r）、对噪声不敏感；
缺点：不一定能找到最优解、取决于初始点的位置、基于欧式距离，假设类是符合椭圆形状的、对高维数据不太适用。

3. DBSCAN

DBSCAN(Density-Based Spatial Clustering of Application with Noise)，基于密度的、对噪声鲁棒的聚类算法。该算法主要基于数据的空间密度进行聚类，将类簇定义为密度相连的点的最大集合，只有目标点周围一定空间范围的对象个数大于所设定的阈值时，才会生成类簇。如果存在单个目标点属于多个类簇的情况，类簇间也会扩展形成新的类簇，这样能够把符合要求的数据都划分到类簇中，不仅可以发现数据集中任意形状的类簇，还可以对数据集中存在的噪声和异常数据进行过滤。

主要参数有邻域半径eps 和密度阈值 min_pts，基本概念包括核心点、边界点、噪声点等。

核心点：对于任意数据点，在其半径为 eps 的邻域内的数据点数量如果超过密度阈值 min_pts，那么该点就是一个核心点。（如下图红色点）
边界点：对于任意数据点，在其半径为 eps 的邻域内的数据点数量如果小于密度阈值 min_pts，但其位于其他核心点的邻域内，那么该点就是一个边界点；（如下图黄色点）
噪声点：对于任意数据点，在其半径为 eps 的邻域内的数据点数量如果小于密度阈值 min_pts，且本身也不属于其他核心点邻域，那么该点就是一个噪声点。（如下图蓝色点）

3.1 算法流程

主要处理流程如下：（首先将所有数据点都标记为未访问）
给定参数：邻域半径 eps，密度阈值 min_pts；

随机选取一个未访问的点 p，对其进行 Radius-NN搜索；
判断该点的近邻点数量是否超过 min_pts？
1. 超过，将 p 记为核心点，并创建一个聚类 C，将 p 标记为已访问点，接着执行步骤3；
2. 未超过，将 p 标记为噪声点，同时状态为已访问。
遍历核心点 p 的所有邻域点，并将这些数据点标记为类C
1. 如果该邻域点也是核心点，则重复步骤3；
取出聚类C的数据点，重复步骤1-3；
直到所有数据点都被标记为已访问。

3.2 代码练习

typedef struct DBSCANCluster{
    std::vector<size_t> core_points;
    std::vector<size_t> neighborhood;
}DBSCANCluster;

class DBSCAN{
public:
    void set_data(const Eigen::MatrixXd& _input_matrix, int leaf_size = 5);
    bool compute(double radius, int min_points);	// 使用unorder_set进行邻居点扩展
    bool compute_copy(double radius, int min_points);	// 使用动态Vector进行邻居点扩展

    // 聚类结果保存和输出
    bool save_cluster_data_to_file(const std::string& file_name);
    void print_clusters();

private:
    bool find_radius_nn(const Eigen::MatrixXd& key, double radius, std::vector<size_t>& neighbors);

private:
    Eigen::MatrixXd _data;
    std::vector<DBSCANCluster> _clusters;

    KDTreeAVLNearestNeighbors _kdtree_nn;    
};

#include "Clustering/DBSCAN.h"

#include <unordered_set>

void DBSCAN::set_data(const Eigen::MatrixXd& input_matrix, int leaf_size){
    _data = input_matrix;
    _kdtree_nn.set_data(input_matrix, leaf_size);
}

bool DBSCAN::compute(double radius, int min_points){
    // 定义访问记录表
    std::vector<bool> visited(_data.cols(), false);
    std::vector<bool> cluster_neighbors(_data.cols(), false);
    std::cout << "data cols: " << _data.cols() << std::endl;

    // 遍历所有数据点
    for(size_t i = 0; i < _data.cols(); ++i){
        if(!visited[i]){
            // 查找当前点的邻域点
            const Eigen::VectorXd& p = _data.col(i);
            std::vector<size_t> neighbors;
            if(!find_radius_nn(p, radius, neighbors)){
                std::cerr << "find_radius_nn failure!" << std::endl;
                return false;
            }

            std::cout << "i: " << i << " ,neighbors: " << neighbors.size() << std::endl;
            // 判断当前点是否为核心点
            if(neighbors.size() < min_points){
                visited[i] = true;
            }else{
                // 为核心点构建新聚类并扩展
                DBSCANCluster cluster;
                cluster.core_points.emplace_back(i);
                cluster.neighborhood.emplace_back(i);
                visited[i] = true;
                cluster_neighbors[i] = true;

                // 邻居点扩展
                std::unordered_set<size_t> neighbors_queue;
                for(size_t k = 0; k < neighbors.size(); ++k){
                    if(!visited[neighbors[k]] && !cluster_neighbors[neighbors[k]]){
                        neighbors_queue.insert(neighbors[k]);

                    }
                }
                while(!neighbors_queue.empty()){
                    // 取出当前点，判断邻域关系
                    size_t index = *neighbors_queue.begin();
                    neighbors_queue.erase(neighbors_queue.begin());
                    const Eigen::MatrixXd& cur_p = _data.col(index);
                    std::vector<size_t> nneighbors;
                    if(!find_radius_nn(cur_p, radius, nneighbors)){
                        std::cerr << "find_radius_nn failure!" << std::endl;
                        return false;
                    }

                    std::cout << "index: " << index << " ,nneighbors: " << nneighbors.size() << std::endl;
                    if(nneighbors.size() < min_points){
                        visited[index] = true;
                        cluster.neighborhood.emplace_back(index);
                        cluster_neighbors[index] = true;
                    }else{
                        cluster.core_points.emplace_back(index);
                        cluster.neighborhood.emplace_back(index);
                        visited[index] = true;
                        cluster_neighbors[index] = true;

                        for(size_t n = 0; n < nneighbors.size(); ++n){
                            if(!visited[nneighbors[n]] && !cluster_neighbors[nneighbors[n]]){
                                neighbors_queue.insert(nneighbors[n]);
                            }
                        }
                    }
                }
                _clusters.emplace_back(cluster);
            }
        }
    }
    return true;
}

bool DBSCAN::compute_copy(double radius, int min_points) {
    std::vector<bool> visited(_data.cols(), false);
    std::vector<bool> cluster_point(_data.cols(), false);  //防止同一个数据点的id被多次添加到cluster.neighborhood

    // 遍历所有数据
    for (size_t i = 0; i < _data.cols(); ++i) {
        if (!visited[i]) {
            std::cout << "To find i = " << i << " neighbors" << std::endl;
            // 寻找邻近点
            const Eigen::VectorXd& data_point = _data.col(i);
            std::vector<size_t> neighbors;
            if (!find_radius_nn(data_point, radius, neighbors)) {
                std::cerr << "find_knn failure" << std::endl;
                return false;
            }

            std::cout << "i: " << i << ", neighbors: " << neighbors.size() << ", " << min_points << std::endl;
            // 判断是否为core point
            if (neighbors.size() >= min_points) {  // core point
                DBSCANCluster cluster;
                cluster.core_points.emplace_back(i);  // set core point
                cluster.neighborhood.emplace_back(i);
                cluster_point[i] = true;
                visited[i] = true;

                // add neighbors
                for (size_t k = 0; k < neighbors.size(); ++k) {
                    if (!visited[neighbors[k]] && !cluster_point[neighbors[k]]) {
                        cluster_point[neighbors[k]] = true;
                        cluster.neighborhood.emplace_back(neighbors[k]);
                    }
                }

                // 以当前点为起点，从他的neighbors中寻找其他core point
                for (size_t k = 0; k < cluster.neighborhood.size(); ++k) {
                    std::cout<< "k: " << k << ", cluster.neighborhood size: " << cluster.neighborhood.size() << std::endl;
                    if (!visited[cluster.neighborhood[k]]) {
                        std::vector<size_t> nneighbors;
                        if (!find_radius_nn(_data.col(cluster.neighborhood[k]), radius, nneighbors)) {
                            std::cerr << "find_knn failure" << std::endl;
                            return false;
                        }

                        std::cout << "k: " << k << ", nneighbors: " << nneighbors.size() << ", " << min_points << std::endl;
                        if (nneighbors.size() >= min_points) {  // 又找到一个core point
                            cluster.core_points.emplace_back(cluster.neighborhood[k]);  // set core point
                            visited[cluster.neighborhood[k]] = true;
                            cluster_point[cluster.neighborhood[k]] = true;
                            
                            // add neighbors
                            for (size_t n = 0; n < nneighbors.size(); ++n) {
                                if (!visited[nneighbors[n]] && !cluster_point[nneighbors[n]]) {
                                    cluster_point[nneighbors[n]] = true;
                                    cluster.neighborhood.emplace_back(nneighbors[n]);
                                }
                            }
                        } else {
                            // 噪声点
                            visited[cluster.neighborhood[k]] = true;
                        }
                    }
                }

                _clusters.emplace_back(cluster);
            } else {
                // 噪声点
                visited[i] = true;
            }
        }
    }
    return true;
}

bool DBSCAN::find_radius_nn(const Eigen::MatrixXd& key, double radius, std::vector<size_t>& neighbors){
    KNNResultRadius knn_result(radius);
    if(!_kdtree_nn.KNN_search_radius(key, knn_result)){
        std::cerr << "KNN_search_radius failed!" << std::endl;
        return false;
    }

    std::vector<DistanceValue> dv = knn_result.get_distance_value();
    neighbors.clear();
    for(const auto& d : dv){
        neighbors.emplace_back(d.value);
    }
    return true;
}

bool DBSCAN::save_cluster_data_to_file(const std::string& file_name){
    std::ofstream ofs(file_name);
    if(!ofs.is_open()){
        std::cerr << "can not open " << file_name << std::endl;
        return false;
    }

    for(const auto& c : _clusters){
        for(size_t i = 0; i < c.neighborhood.size(); ++i){
            ofs << _data(0, c.neighborhood[i]) << " " << _data(1, c.neighborhood[i]) << " ";
        }
        ofs << std::endl;
    }

    ofs.close();
    std::cout << "save result to " << file_name << std::endl;
    return true;
}

void DBSCAN::print_clusters() {
    std::cout << "===== DBSCAN clusters =====" << std::endl;
    for (const auto& c : _clusters) {
        std::cout << "core_point index: size: " << c.core_points.size() << ", ";
        for (size_t i = 0; i < c.core_points.size(); ++i) {
            std::cout << c.core_points[i] << " ";
        }
        std::cout << std::endl;

        std::cout << "neighborhood index: size: " << c.neighborhood.size() << ", ";
        for (size_t i = 0; i < c.neighborhood.size(); ++i) {
            std::cout << c.neighborhood[i] << " ";
        }
        std::cout << std::endl;
    }
    std::cout << "===========================" << std::endl;
}