论文《Deep graph tensor learning for temporal link prediction》阅读
- 论文概况
- Introduction
- Related work
- 动态图表示学习
- 图张量表示
- Preliminary
- 张量生成建模
- 深度图张量学习模型
- A.基于图紧凑的空间表示
- B.时间模式表示
- C.时空特征聚合
- D.损失函数
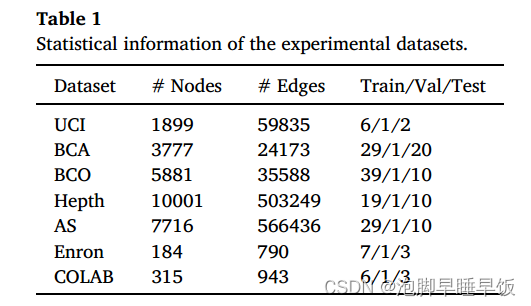
- 实验
- 消融实验
- 总结
论文概况
本文是2024年Information Science上的一篇论文,该篇文章聚焦于使用GNN和自注意力网络来解决绘画推荐问题,提出了GCSAN(Graph Contextualized Self-Attention Network)模型。
Introduction
传统的基于动态图的学习存在一定的局限性:
- 基于循环神经网络的图学习框架学习效率较低
- 图演化的动态机制可能与一般的时间建模技术不太匹配,导致图训练的效果低于预期
针对上述问题,
(i)文章提出了一种基于图张量学习的时间图快照嵌入方法,它可以同时捕获空间结构特征和动态演化特征。
(ii)通过图压缩技术压缩多个时间图快照,可以大大提高动态图表示学习的效率。
Related work
动态图表示学习
对时间图进行建模有两种主要的技术方法。
一种方法是直接对动态图数据进行建模:
- LSTM 网络: LSTM 网络通过保留历史快照的隐藏状态来处理时间动态。
- 使用 GCN 来嵌入每个子图,并使用 GRU 来训练节点嵌入。
- 结合 VGAE [20] 和 GCN-GRU 对每个时间步的节点分布进行建模。
- GSNOP:使用神经过程和神经常微分方程(ODE)来捕获图结构的时间演化。
另一种方法是将动态图间接投影到隐藏空间中:
- EloveGCN:对GCN参数的时间变化而不是节点嵌入进行建模。
- DGCN:最大化了局部和全局图表示之间的互信息,并使用EvolveGCN通过LSTM训练GCN权重。
- HTGN:利用二分几何来映射时间信息,并使用二分图神经网络和二分门控循环神经网络来捕获时空特征。
论文提出的方法与这些方法不同,避免使用 RNN 并直接提取链接信息的时间模式来对动态图进行建模,这可以确保更高的计算效率。
图张量表示
图张量表示学习在过去十年中也受到了广泛的关注,但大多数研究都集中在并解决了多视图图表示问题。
- RTGNN:通过增强图间和图内聚合来更有效地执行多视图图表示学习。
- NTD:是最流行的张量数据表示技术之一。根据多种内在线索(流结构和监督信息),提出的一种广义图正则化NTD(GNTD)框架。
- LRTG :从“干净”的表示张量而不是从受污染的原始数据中学习自适应亲和矩阵。
通过 Tucker 分解,表示张量具有低秩属性。同样针对多视图聚类问题,Wu等人提出了一种新颖的统一图和低秩张量学习(UGLTL)方法[29]用于多视图聚类。与传统方法不同,一方面,UGLTL 基于投影图学习来学习视图特定的亲和力矩阵。另一方面,UGTLL 将亲和力矩阵重新组织为张量形式,并基于低秩张量近似学习其内在张量。 Yu等人提出了图正则化非负张量环分解(GNTR)[30],GNTR方法在聚类和分类任务中比最先进的方法取得了更好的性能。
然而,这些方法没有考虑动态图的时间维度,无法捕捉图结构和语义的动态变化。我们的工作是将图张量表示应用于时态图学习问题的新尝试。
Preliminary

在本研究中,动态属性网络被定义为在
T
\mathcal{T}
T 时间间隔内演化的无向图的一系列离散快照,可以表示为
G
=
{
G
t
}
t
=
1
T
\mathcal{G}=\{G^t\}_{t=1}^T
G={Gt}t=1T 对于每个时间间隔
t
t
t,图快照
G
′
G^\prime
G′ 由节点集
V
t
V^t
Vt和相应的节点属性矩阵
X
t
∈
R
[
V
˙
]
×
d
X^t\in\mathbb{R}^{[\dot{V}]\times d}
Xt∈R[V˙]×d以及边集
E
t
⊂
V
t
×
V
t
E^t\subset V_t\times V_t
Et⊂Vt×Vt组成,使得
G
t
=
(
V
t
,
E
t
,
X
t
)
G^t=(V^t,E^t,X^t)
Gt=(Vt,Et,Xt) 。在本文中,仅考虑边的变化,因此假设每个快照中的图具有固定大小,即
∣
V
t
∣
=
∣
V
∣
|V^t|=|V|
∣Vt∣=∣V∣。在动态属性网络中,时间链接预测的任务有以下定义:给定观察到的图快照
G
∘
G^{\circ}
G∘,使用观察到的时间图
min
∑
i
=
1
τ
C
(
E
r
e
a
l
T
+
i
,
E
~
T
+
i
)
s
.
t
.
{
E
~
T
+
1
,
…
,
E
~
T
+
τ
}
=
M
(
G
o
,
Θ
)
(1)
\begin{aligned}\min\sum_{i=1}^\tau\mathscr{C}(E_{real}^{\mathcal{T}+i},\tilde{E}^{\mathcal{T}+i})\\s.t.\quad\{\tilde{E}^{\mathcal{T}+1},\ldots,\tilde{E}^{\mathcal{T}+\tau}\}=\mathcal{M}(\mathcal{G}^o,\Theta)\end{aligned}\tag{1}
mini=1∑τC(ErealT+i,E~T+i)s.t.{E~T+1,…,E~T+τ}=M(Go,Θ)(1)
其中
E
~
T
+
i
\tilde{E}^{\mathcal{T}+i}
E~T+i是图在时间间隔
T
+
i
\mathcal{T}+i
T+i处的预测边,
C
(
⋅
)
\mathscr{C}(\cdot)
C(⋅)是误差函数,用于测量图中的真实边
E
r
e
a
l
T
+
i
E_{real}^{\mathcal{T}+i}
ErealT+i与预测边之间的误差。根据统计学习理论,时间链路预测的本质是估计图的成对节点之间的连接在时间跨度
(
T
+
1
,
T
+
τ
)
(\mathcal{T}+1,\mathcal{T}+\tau)
(T+1,T+τ)内的概率分布。因此,预测边的联合概率分布为
P
(
E
~
T
+
1
,
…
,
E
~
T
+
τ
,
G
o
)
=
P
(
E
~
T
+
1
,
…
,
E
~
T
+
τ
∣
G
o
)
P
(
G
o
)
=
∏
i
=
1
τ
P
(
E
~
T
+
i
∣
G
o
)
P
(
G
o
)
.
(2)
\begin{aligned}&P(\tilde{E}^{\mathcal{T}+1},\ldots,\tilde{E}^{\mathcal{T}+\tau},\mathcal{G}^o)=P(\tilde{E}^{\mathcal{T}+1},\ldots,\tilde{E}^{\mathcal{T}+\tau}|\mathcal{G}^o)P(\mathcal{G}^o)\\&=\prod_{i=1}^\tau P(\tilde{E}^{\mathcal{T}+i}|\mathcal{G}^o)P(\mathcal{G}^o).\end{aligned}\tag{2}
P(E~T+1,…,E~T+τ,Go)=P(E~T+1,…,E~T+τ∣Go)P(Go)=i=1∏τP(E~T+i∣Go)P(Go).(2)
张量生成建模
由于观察到的时间网络的每个图快照都可以表示为邻接矩阵
A
t
A^{t}
At 和属性矩阵
X
t
X^{t}
Xt ,因此一段时间内观察到的整个动态网络可以形式化为 3 阶张量的二元组
G
o
=
(
A
o
∈
{
0
,
1
}
∣
V
∣
×
∣
V
∣
×
T
,
X
o
∈
R
∣
V
∣
×
d
×
T
)
\mathcal{G}^o=(\mathscr{A}^o\in\{0,1\}^{|V|\times|V|\times\mathcal{T}},\mathscr{X}^o\in\mathbb{R}^{|V|\times d\times\mathcal{T}})
Go=(Ao∈{0,1}∣V∣×∣V∣×T,Xo∈R∣V∣×d×T),其中
A
o
\mathscr{A}^{o}
Ao 是邻接张量或结构张量,
X
o
\mathscr{X}^{o}
Xo是属性张量。如果应用模 𝑡 张量矩阵化(又名,在维度 𝑡 上展开),则有
A
o
=
[
[
A
1
,
A
2
,
⋅
⋅
⋅
,
A
T
]
]
\mathscr{A}^o=[[A_1,A_2,\cdotp\cdotp\cdotp,A_T]]
Ao=[[A1,A2,⋅⋅⋅,AT]] 和
X
o
=
[
[
X
1
,
X
2
,
⋯
,
X
T
]
]
\mathcal{X}^o=[[X_1,X_2,\cdots,X_T]]
Xo=[[X1,X2,⋯,XT]]。
另外,从时间
T
\mathcal{T}
T+ 1 到时间
T
\mathcal{T}
T + 𝜏 之间要预测的图拓扑可以表示为三阶邻接张量
[
[
A
T
+
1
,
A
T
+
2
,
⋅
⋅
⋅
,
A
T
+
τ
]
]
∈
{
0
,
1
}
∣
V
∣
×
∣
V
∣
×
τ
[[A_{\mathcal{T}+1},A_{\mathcal{T}+2},\cdotp\cdotp\cdotp,A_{\mathcal{T}+\tau}]]\in\{0,1\}^{|V|\times|V|\times\tau}
[[AT+1,AT+2,⋅⋅⋅,AT+τ]]∈{0,1}∣V∣×∣V∣×τ.与静态网络上的缺失链接预测不同,静态网络上的缺失链接预测可以形式化为图邻接矩阵补全问题,时间链接预测实际上是一个 model-t 张量生成问题,如图 1 所示,因为张量
A
F
\mathscr{A}^{\mathcal{F}}
AF中的未知条目是时间-取决于观察到的图张量
A
0
\mathscr{A}^{\mathcal{0}}
A0中的那些。因此,时间链接预测的目标是学习一个张量预测函数,生成一个预测张量
A
F
∈
R
∣
V
∣
×
∣
V
∣
×
τ
\mathscr{A}^{\mathcal{F}}\in\mathbb{R}^{|V|\times|V|\times\tau}
AF∈R∣V∣×∣V∣×τ
使得:
min
∥
A
^
F
−
A
F
∥
F
2
s
.
t
.
A
^
F
=
P
(
A
o
,
X
o
;
Θ
)
(3)
\begin{aligned}\min\|\hat{\mathscr{A}}^{\mathcal{F}}-\mathscr{A}^{\mathcal{F}}\|_F^2\mathrm{~s.t.~}\hat{\mathscr{A}}^{\mathcal{F}}=\mathcal{P}(\mathscr{A}^o,\mathscr{X}^o;\Theta)\end{aligned}\tag{3}
min∥A^F−AF∥F2 s.t. A^F=P(Ao,Xo;Θ)(3)
其中 ‖ ⋅ ‖𝐹 是张量 Frobenius 范数,定义为
min
∥
A
^
F
−
A
F
∥
F
=
∑
i
∑
j
∑
t
(
A
^
i
,
j
,
t
F
−
A
i
,
j
,
t
F
)
2
(4)
\begin{aligned}\min\|\hat{\mathscr{A}}^F-\mathscr{A}^F\|_F=\sqrt{\sum_i\sum_j\sum_t(\hat{\mathscr{A}}_{i,j,t}^F-\mathscr{A}_{i,j,t}^F)^2}\end{aligned}\tag{4}
min∥A^F−AF∥F=i∑j∑t∑(A^i,j,tF−Ai,j,tF)2(4)
由于生成目标张量的关键是估计张量在三个维度上的概率分布,因此上述问题可以转化为概率张量生成问题。
P
(
A
F
,
A
o
,
X
o
;
Θ
)
=
P
(
A
F
∣
A
o
,
X
o
;
Θ
)
P
(
A
o
,
X
o
;
Θ
)
(5)
\begin{aligned}P(\mathscr{A}^{\mathcal{F}},\mathscr{A}^{o},\mathscr{X}^{o};\Theta)=P(\mathscr{A}^{\mathcal{F}}|\mathscr{A}^{o},\mathscr{X}^{o};\Theta)P(\mathscr{A}^{o},\mathscr{X}^{o};\Theta)\end{aligned}\tag{5}
P(AF,Ao,Xo;Θ)=P(AF∣Ao,Xo;Θ)P(Ao,Xo;Θ)(5)
为了优化预测模型的参数,我们的目标通过最大化等式中的后验概率进一步形式化为最大似然估计问题。
Θ
=
arg
max
Θ
P
(
A
^
F
∣
A
o
,
X
o
;
Θ
)
=
arg
max
Θ
∏
t
∏
i
,
j
p
(
A
^
i
,
j
,
t
F
∣
A
o
,
X
o
;
Θ
)
.
(6)
\begin{aligned}\Theta&=\arg\max_\Theta P(\hat{\mathscr{A}}^\mathcal{F}|\mathscr{A}^o,\mathscr{X}^o;\Theta)\\&=\arg\max_\Theta\prod_t\prod_{i,j}p(\hat{\mathscr{A}}_{i,j,t}^F|\mathscr{A}^o,\mathscr{X}^o;\Theta).\end{aligned}\tag{6}
Θ=argΘmaxP(A^F∣Ao,Xo;Θ)=argΘmaxt∏i,j∏p(A^i,j,tF∣Ao,Xo;Θ).(6)
为了计算方便,可以将其改为对数形式
Θ
=
arg
max
Θ
∑
i
,
j
,
t
log
p
(
A
^
i
,
j
,
t
F
∣
A
o
,
X
o
;
Θ
)
=
arg
max
Θ
E
A
i
,
j
,
t
F
∼
P
A
F
log
p
(
A
^
i
,
j
,
t
F
∣
A
o
,
X
o
;
Θ
)
.
(7)
\begin{aligned}\Theta&=\arg\max_\Theta\sum_{i,j,t}\log p(\hat{\mathscr{A}}_{i,j,t}^\mathcal{F}|\mathscr{A}^o,\mathscr{X}^o;\Theta)\\&=\arg\max_\Theta\mathbb{E}_{\mathscr{A}_{i,j,t}^\mathcal{F}\sim P_{\mathscr{A}^\mathcal{F}}}\log p(\hat{\mathscr{A}}_{i,j,t}^\mathcal{F}|\mathscr{A}^o,\mathscr{X}^o;\Theta).\end{aligned}\tag{7}
Θ=argΘmaxi,j,t∑logp(A^i,j,tF∣Ao,Xo;Θ)=argΘmaxEAi,j,tF∼PAFlogp(A^i,j,tF∣Ao,Xo;Θ).(7)
深度图张量学习模型
为了估计图邻接张量
A
^
\hat{\mathscr{A}}
A^ 在时间跨度 (
T
\mathcal{T}
T+ 1 ,
T
\mathcal{T}
T + 𝜏 ) 内的每个条目的存在概率,我们引入了深度图张量学习技术。对于观察到的动态网络
G
∘
G^{\circ}
G∘,我们通过两种方式进行研究,即提出基于图紧凑的空间表示来捕获图结构信息,并提出时间模式表示来学习图演化信息。称为 DGTL 的整个计算框架如图所示。
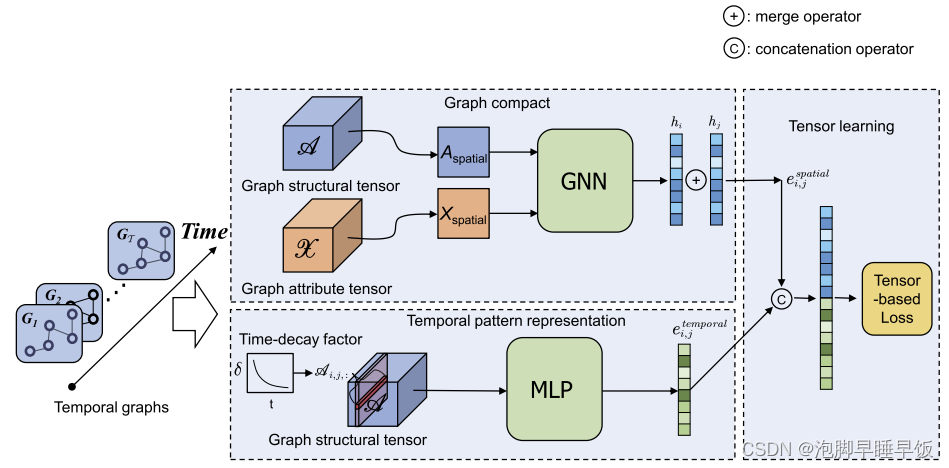
A.基于图紧凑的空间表示
对于观察到的图快照,我们特别在压缩的动态图上应用图神经网络,而不是使用循环神经网络来迭代地跨多个图快照学习模型。这样做,可以显着提高学习效率。为此,给定时间跨度[1, 𝑇]内动态图的邻接张量
A
o
\mathscr{A}^{o}
Ao,我们将邻接张量压缩为加权邻接矩阵
A
s
p
a
t
i
a
l
A_{spatial}
Aspatial,表示动态图在一段时间内的空间结构信息。使用模-𝑡积[32],我们有
A
s
p
a
t
i
a
l
=
A
o
×
t
Λ
=
λ
1
A
⋮
,
⋮
,
1
o
+
λ
2
A
⋮
,
⋮
,
2
o
+
⋯
+
λ
T
A
⋮
,
⋮
,
T
o
=
∑
t
=
1
T
λ
t
A
:
,
:
,
t
o
,
(8)
\begin{aligned} A_{spatial}& =\mathscr{A}^{o}\times_{t}\Lambda \\ &=\lambda_{1}\mathscr{A}_{\vdots,\vdots,1}^{o}+\lambda_{2}\mathscr{A}_{\vdots,\vdots,2}^{o}+\cdots+\lambda_{T}\mathscr{A}_{\vdots,\vdots,T}^{o} \\ &=\sum_{t=1}^{\mathcal{T}}\lambda_{t}\mathcal{A}_{:,:,t}^{o}, \end{aligned}\tag{8}
Aspatial=Ao×tΛ=λ1A⋮,⋮,1o+λ2A⋮,⋮,2o+⋯+λTA⋮,⋮,To=t=1∑TλtA:,:,to,(8)
其中
A
:
,
:
,
1
o
,
A
:
,
:
,
2
o
,
⋯
,
A
:
,
:
,
T
o
\mathscr{A}_{:,:,1}^o,\mathscr{A}_{:,:,2}^o,\cdots,\mathscr{A}_{:,:,T}^o
A:,:,1o,A:,:,2o,⋯,A:,:,To 是
A
o
\mathscr{A}^{o}
Ao的切片,
Λ
=
(
λ
1
,
λ
2
,
⋯
λ
T
)
∈
R
T
\Lambda=(\lambda_1,\lambda_2,\cdots\lambda_T)\in\mathbb{R}^T
Λ=(λ1,λ2,⋯λT)∈RT是可学习的参数向量。对于观察到的动态图的属性张量
X
o
\mathscr{X}^o
Xo,我们可以使用类似的方法将其压缩为加权属性矩阵。
X
s
p
a
t
i
a
l
=
X
o
×
t
Λ
=
λ
1
X
⋮
,
⋮
,
1
o
+
λ
2
X
⋮
,
⋮
,
2
o
+
⋯
+
λ
T
X
⋮
,
⋮
,
T
o
=
∑
t
=
1
T
λ
t
X
⋮
,
⋮
,
t
o
(9)
\begin{aligned} X_{spatial}& =X^{o}\times_{t}\Lambda \\ &=\lambda_{1}X_{\vdots,\vdots,1}^{o}+\lambda_{2}X_{\vdots,\vdots,2}^{o}+\cdots+\lambda_{T}X_{\vdots,\vdots,T}^{o} \\ &=\sum_{t=1}^{T}\lambda_{t}X_{\vdots,\vdots,t}^{o} \end{aligned}\tag{9}
Xspatial=Xo×tΛ=λ1X⋮,⋮,1o+λ2X⋮,⋮,2o+⋯+λTX⋮,⋮,To=t=1∑TλtX⋮,⋮,to(9)
参数向量
Λ
\Lambda
Λ是
A
o
\mathscr{A}^{o}
Ao和
X
o
\mathscr{X}^o
Xo共享的。接下来,将聚合的图邻接矩阵和图属性矩阵输入到图神经网络(例如 GCN)中,以生成节点的嵌入矩阵
H
s
p
a
t
i
a
l
=
G
N
N
(
A
s
p
a
t
i
a
l
,
X
s
p
a
t
i
a
l
;
Φ
)
(10)
\begin{aligned}H_{spatial}=GNN(A_{spatial},X_{spatial};\Phi)\end{aligned}\tag{10}
Hspatial=GNN(Aspatial,Xspatial;Φ)(10)
B.时间模式表示
虽然传统方法通常利用 LSTM 或 GRU 等循环神经网络来学习时间图快照之间的时间相关关系,但这里我们放弃了这种学习范式,直接从图邻接张量中提取时间相关向量,从而有效地捕获动态图中边缘的时间演化模式,显着提高模型的训练效率。对于观察到的时间图中的每个节点对 (𝑖,𝑗),它被初始化为时间向量。
ℏ
i
,
j
=
Δ
⊙
A
i
,
j
,
:
o
=
(
δ
1
A
i
,
j
,
1
o
,
δ
2
A
i
,
j
,
2
o
,
⋯
,
δ
t
A
i
,
j
,
t
o
,
⋯
,
δ
T
A
i
,
j
,
T
o
)
,
(11)
\begin{aligned} \hbar_{i,j}& =\Delta\odot\mathscr{A}_{i,j,:}^{o} \\ &=(\delta_{1}\mathscr{A}_{i,j,1}^{o},\delta_{2}\mathscr{A}_{i,j,2}^{o},\cdots,\delta_{t}\mathscr{A}_{i,j,t}^{o},\cdots,\delta_{\mathcal{T}}\mathscr{A}_{i,j,\mathcal{T}}^{o}), \end{aligned}\tag{11}
ℏi,j=Δ⊙Ai,j,:o=(δ1Ai,j,1o,δ2Ai,j,2o,⋯,δtAi,j,to,⋯,δTAi,j,To),(11)
其中
A
i
,
j
,
:
o
\mathscr{A}_{i,j,:}^{o}
Ai,j,:o为模型-𝑡纤维,
δ
t
=
e
x
p
(
−
α
t
(
T
−
t
)
)
,
α
t
=
0.8
,
t
∈
[
1
,
T
]
\delta_{t}=exp(-\alpha_{t}(\mathcal{T}-t)),\alpha_{t}=0.8,t\in[1,\mathcal{T}]
δt=exp(−αt(T−t)),αt=0.8,t∈[1,T]为时间衰减因子,⊙ 为元素- 明智的乘法。与先前的图快照相比,时间衰减因子可以为较新的图快照分配更高的权重。这是受到人类记忆特征的启发(也称为遗忘曲线,),其中较早的图形快照容易被遗忘,而较新的图形快照则被更清晰地记住。因此,借助时间衰减因子,DGTL 可以更好地捕获时间图的演化模式。这里,我们选择 MLP 作为编码方法来生成边缘嵌入向量
e
i
,
j
t
e
m
p
o
r
a
l
e_{i,j}^{temporal}
ei,jtemporal 。所以,我们有
e
i
,
j
t
e
m
p
o
r
a
l
=
M
L
P
(
ℏ
i
,
j
;
Ψ
)
(12)
e_{i,j}^{temporal}=MLP(\hbar_{i,j};\Psi)\tag{12}
ei,jtemporal=MLP(ℏi,j;Ψ)(12)
C.时空特征聚合
我们利用从图压缩过程中获得的节点嵌入向量来生成基于空间特征的边缘向量。
e
i
,
j
s
p
a
t
i
a
l
=
h
i
⊕
h
j
(13)
e_{i,j}^{spatial}=h_i\oplus h_j\tag{13}
ei,jspatial=hi⊕hj(13)
其中 ⊕ 是逐元素加法运算符。然后,边缘表示由获得的空间向量和时间向量加权连接为
e
i
,
j
=
η
e
t
e
m
p
o
r
a
l
i
,
j
∣
∣
(
1
−
η
)
e
s
p
a
t
i
a
l
i
,
j
η
∈
[
0
,
1
]
(14)
e_{i,j}=\eta e_{temporal}^{i,j}||(1-\eta)e_{spatial}^{i,j} \eta\in[0,1]\tag{14}
ei,j=ηetemporali,j∣∣(1−η)espatiali,jη∈[0,1](14)
与 GAE 类似,张量
A
F
{\mathscr{A}}^{\mathcal{F}}
AF中节点对的估计边存在概率由下式计算:
p
^
(
A
i
,
j
,
t
F
=
1
)
=
σ
(
⟨
e
i
,
j
T
,
e
i
,
j
⟩
)
φ
t
(15)
\hat{p}(\mathcal{A}_{i,j,t}^{\mathcal{F}}=1)=\sigma(\left\langle e_{i,j}^{T},e_{i,j}\right\rangle)\varphi_{t}\tag{15}
p^(Ai,j,tF=1)=σ(⟨ei,jT,ei,j⟩)φt(15)
其中 𝜎(⋅) 是 sigmoid 激活函数,⟨𝑎, 𝑏⟩ 表示两个向量的内积。时间衰减因子
φ
t
=
e
x
p
(
−
α
t
(
t
−
T
−
1
)
)
,
t
∈
[
T
+
1
,
T
+
τ
]
\varphi_{t}=exp(-\alpha_{t}(t-\mathcal{T}-1)),t\in[\mathcal{T}+1,\mathcal{T}+\tau]
φt=exp(−αt(t−T−1)),t∈[T+1,T+τ]的作用与
δ
t
\delta_{t}
δt类似。
D.损失函数
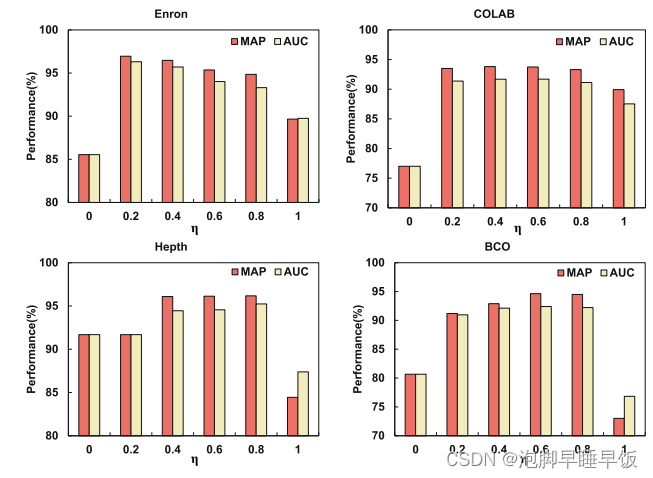
为了以监督的方式训练模型参数,观察到的图快照按时间顺序分为两部分。从 𝑡 = 1 到 𝑡 = 𝜂 的图张量(包括邻接张量 𝒜𝜂 和属性张量 𝒳𝜂)用作训练数据,而从 𝑡 = 𝜂 + 1 到
t
=
T
t=\mathcal{T}
t=T的其余图邻接张量
A
T
−
η
\mathscr{A}^{T-\eta}
AT−η被视为验证数据。请注意,由于我们关注验证数据中的图结构信息,因此不考虑图属性张量。验证数据的似然函数为
L
=
∏
i
,
j
,
{
t
}
η
+
1
T
p
^
(
A
i
,
j
,
t
=
1
)
γ
i
,
j
,
t
(
1
−
p
^
(
A
i
,
j
,
t
=
1
)
)
(
1
−
γ
i
,
j
,
t
)
(16)
L=\prod_{i,j,\{t\}_{\eta+1}^{\mathcal{T}}}\hat{p}(\mathscr{A}_{i,j,t}=1)^{\gamma^{i,j,t}}(1-\hat{p}(\mathscr{A}_{i,j,t}=1))^{(1-\gamma^{i,j,t})}\tag{16}
L=i,j,{t}η+1T∏p^(Ai,j,t=1)γi,j,t(1−p^(Ai,j,t=1))(1−γi,j,t)(16)
其中
γ
i
,
j
,
t
∈
{
0
,
1
}
\gamma^{i,j,t}\in\{0,1\}
γi,j,t∈{0,1},链接预测的损失函数定义为:
L
l
p
=
−
E
A
i
,
j
,
t
∼
Ω
+
log
p
^
(
A
i
,
j
,
t
=
1
)
−
E
A
i
,
j
,
t
∼
Ω
−
log
(
1
−
p
^
(
A
i
,
j
,
t
=
1
)
)
\mathcal{L}_{lp}=-\mathbb{E}_{\mathcal{A}_{i,j,t}\sim\Omega^{+}}\log\hat{p}(\mathcal{A}_{i,j,t}=1)-\mathbb{E}_{\mathcal{A}_{i,j,t}\sim\Omega^{-}}\log(1-\hat{p}(\mathcal{A}_{i,j,t}=1))
Llp=−EAi,j,t∼Ω+logp^(Ai,j,t=1)−EAi,j,t∼Ω−log(1−p^(Ai,j,t=1))
其中Ω+表示正采样的空间,Ω−对应于时间跨度
[
η
+
1
,
T
]
[\eta+1,\mathcal{T}]
[η+1,T]内的图形快照中负采样的空间。请注意,
L
l
p
\mathcal{L}_{lp}
Llp 是等式 1 中所示误差函数的实现。受用于过滤训练数据中的噪声信息的低秩近似的启发,进一步引入张量的核范数作为调节项
L
n
u
=
∥
A
T
∥
⊗
=
∑
t
=
1
η
T
r
(
[
(
A
⋮
,
⋮
,
t
T
)
T
A
⋮
,
⋮
,
t
T
]
1
/
2
)
,
(18)
\begin{aligned} \mathcal{L}_{nu}& =\|\mathscr{A}^{\mathcal{T}}\|_{\otimes} \\ &=\sum_{t=1}^{\eta}Tr\left([(\mathscr{A}_{\vdots,\vdots,t}^{T})^{T}\mathscr{A}_{\vdots,\vdots,t}^{T}]^{1/2}\right), \end{aligned}\tag{18}
Lnu=∥AT∥⊗=t=1∑ηTr([(A⋮,⋮,tT)TA⋮,⋮,tT]1/2),(18)
其中 𝑇 𝑟(⋅) 表示矩阵迹函数。最终的损失函数为
L
=
L
l
p
+
ρ
L
n
u
(19)
\mathcal{L}=\mathcal{L}_{lp}+\rho\mathcal{L}_{nu}\tag{19}
L=Llp+ρLnu(19)
其中𝜌是一个超参数,本文根据现实数据集的经验验证将其设置为0.1。基于损失函数,可以对所提出的深度图张量学习模型实现端到端训练。
实验
我们将最后一个物品作为局部兴趣,然后将局部兴趣和计算出的自注意力结果加权结合,作为最终的用户兴趣。

消融实验
总结
本文提出了一种有效的动态图嵌入方法,称为 DGTL,用于时间链接预测。 DGTL 与传统的动态图学习方法不同,它避免使用循环神经网络来识别时间相关信息。相反,我们建议使用时间序列因素来学习时间链接的历史变化模式,并生成反映图的动态变化的时间耦合链接级嵌入向量。此外,我们将随时间变化的图快照表示为张量,并通过图紧凑技术使用单个图神经网络模型来捕获图的结构特征,从而实现节点级空间特征嵌入。最后,我们融合上述两个嵌入向量,通过适当地结合时空图演化信息来预测动态图中的时间链接。根据七个开放动态图的实验结果,所提出模型的三个变体取得了组合最佳结果,在七个数据集中的六个上超越了所有最先进的(SOTA)动态图学习方法。此外,由于避免使用循环神经网络作为时间序列相关的训练方法,与传统的基于 RNN 的动态图学习模型相比,我们的模型的训练效率显着提高。