小林最近遇到一个问题：“对于任意给定的一个正整数n，统计其阶乘n！的末尾中0的个数”，这个问题究竟该如何解决？

• 先用n=5来解决这个问题。n的阶乘即n!=5!=5*4*3*2*1=120，显然应该为2个数相乘等于10才能得到一个结尾0，仔细遍历1,2,3…10，发现只有2*5=10才是得到末尾0的唯一方式。

• 而n!中5的倍数个数小于2的倍数个数，所以n!的末尾的0的个数应为：n!中每个个数中5的倍数的个数之和。所以代码如下：

#includeint main(int argc,char *argv[])
{
int n;
int sum=0;
int i, k;
printf("Pleast input a positive number: ");
scanf("%d",&n);            //循环控制变量
long long multiply=1L;
int j;
for(j=n;j>=1;--j){
    multiply*=j;
}
printf("The factorial of %d is:%ld\n",n,multiply);
for(i=5; i<=n; i=i+5)      //只有5的倍数才含5的因子
{
    int m=i;
    for(k=0; m%5==0; k++)
        m=m/5;
    sum=sum+k;
}
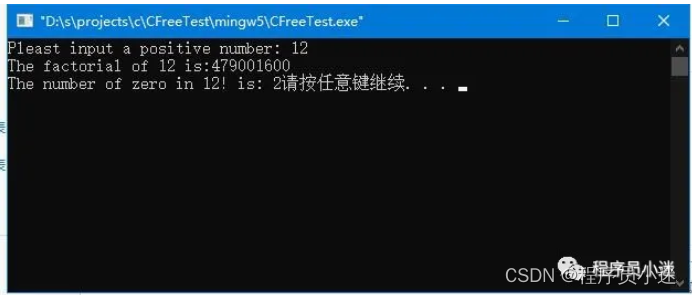
printf("The number of zero in %d! is: %d",n,sum);
return 0;
}

注意
这个问题的通常解法是：求出n!的值，然后再算出结尾0的个数。但这样做有个问题，就是n!在n=13及以上时就已经非常大了，已经溢出了long long型整数所能保存的最大值。也就是说，在n=13及以上时不能用通常解法。这就是本篇文章解法的意义，这也是许多此类面试题的解法。
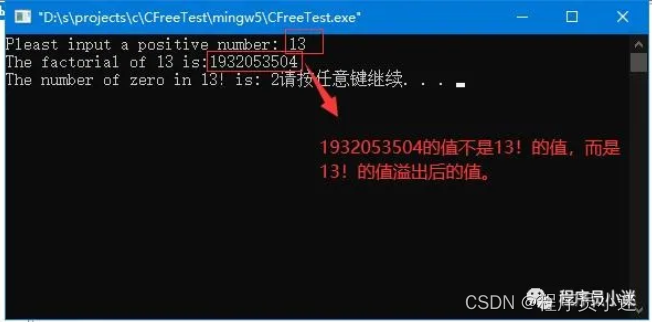
13！=6,227,020,800‬，但下图显示的13！的结果为1932053504，这是溢出long long整型值后的值。
溢出示意图如下：

• 如何计算溢出后的值是多少？
  拿13！=6,227,020,800来举例，保存它的值的数据类型为long long，大小为4个字节，最大值为2147483648，用6227020800%2147483648得出的值即为1932053504。这个值就是示例中显示出来的结果，但它的值已被截取了。

• 如何心算出本篇文章给出的面试题？
  拿26！举例，先取出可以得出结尾0的单个数：5、10、15、20、25。再求出每个数字的以5为底的对数值的floor值，再求出这些值之和即为答案。如下图：

---

微风不燥，阳光正好，你就像风一样经过这里，愿你停留的片刻温暖舒心。

我是程序员小迷（致力于C、C++、Java、Kotlin、Android、Shell、JavaScript、TypeScript、Python等编程技术的技巧经验分享），若作品对您有帮助，请关注、分享、点赞、收藏、在看、喜欢，您的支持是我们为您提供帮助的最大动力。

欢迎关注。助您在编程路上越走越好！